-
相对论皮秒激光与低密度等离子体作用可以通过“激光直接加速”机制获得超有质动力定标率的高能电子, 且电荷量可以达到百nC级, 在伽马射线产生、正电子产生等方面具有重要应用. 然而激光直接加速电子束相比激光尾场加速电子束具有更大的发散角, 同时实验观测的横向束分布也不均匀, 但是其中的物理机制研究较少. 本文通过二维粒子模拟证明, 相对论皮秒激光在低密度等离子体中驱动的激光直接加速中, 高能电子束会在激光偏振方向分叉, 而且电子能量越高这种现象越明显. 文章通过细致的理论分析解释了这种高能电子横向分布产生“分叉”结构的内在原因. 在激光直接加速的过程中, 电子在纵向获得加速的时候, 它在激光偏振方向(横向) betatron振荡的动能也会随之增加, 当电子的能量足够高时, 二者呈线性关系, 因此高能电子的横向速度的振幅近似相等, 这种相等的振幅最终导致了高能电子束在激光偏振方向的分叉.Energetic electron beam can be generated through the directlaser acceleration (DLA) mechanism when high power picosecond laser propagates in underdense plasma, and the electron yield can reach several hundred nC, which has a great application in driving secondary radiations, such as bremsstrahlung radiation and betatron radiation. When a linearly polarized laser is used, the beam divergence is always larger in the laser polarization direction. What is more, the forked spectral-spatial distribution is observed in the experiments driven by femtosecond laser where DLA is combined with the laser wakefield acceleration (LWFA). The forked distribution is regarded as an important feature of DLA. However, an analytical explanation for both the bigger divergence and the forked spectral-spatial distribution is still lacking. Two-dimensional (2D) particle-in-cell simulations of picosecond laser propagating in underdense plasma are conducted in this paper to show how the fork is formed in DLA. The fork structure is a reflection of the distribution of electron transverse velocity. We find that when electrons are accelerated longitudinally, the transverse oscillation energy in the laser polarization direction increases correspondingly. If the electron energy is high enough, the transverse oscillation energy will increase linearly with the electron energy. As a result, the most energetic electrons will have an equal amplitude of vy, where vy denotes the velocity in the laser polarization direction. For a single electron, the distribution of its transverse velocity over a long period
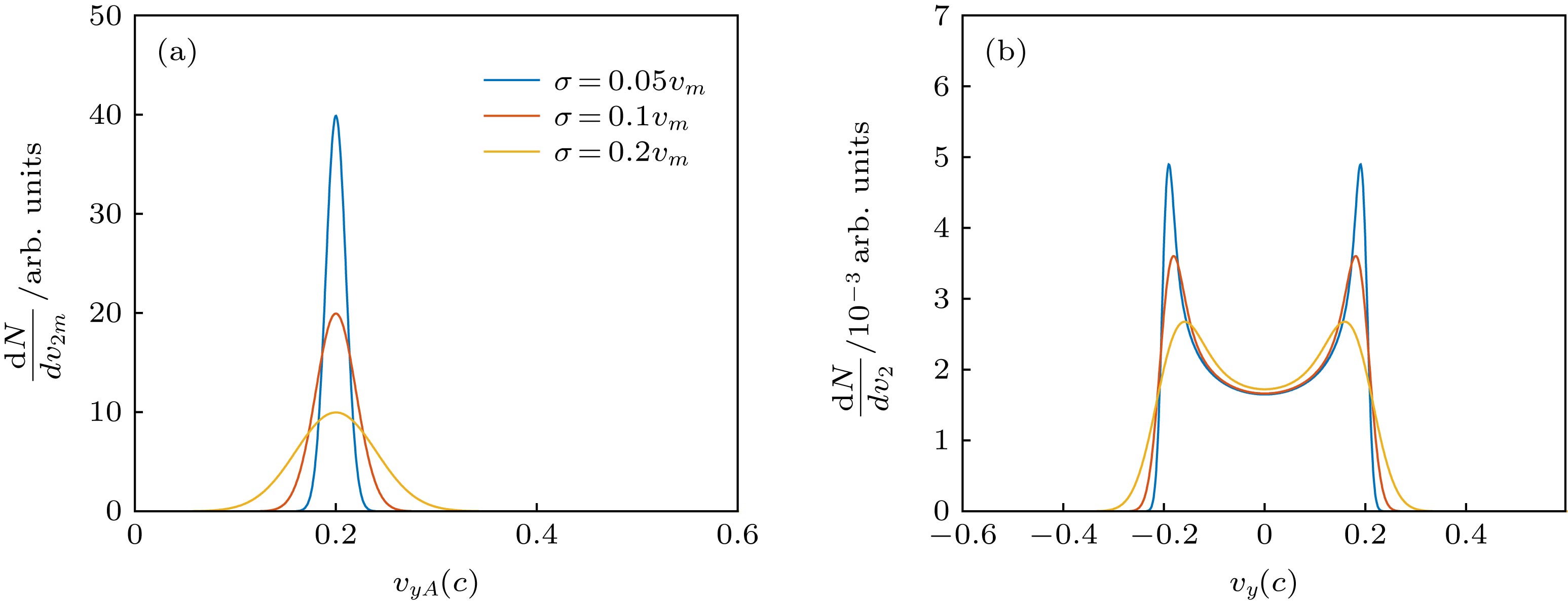
$\dfrac{{{\rm d}P}}{{{\rm d}{v_y}}}$ , will peak at ±vm (vm denotes the amplitude of vy). If all the electrons have the same vm, the distribution of vy at a given time will be the same as$\dfrac{{{\rm d}P}}{{{\rm d}{v_y}}}$ . That means they will split transversely, leading to a forked spectral-spatial distribution. By using a simplified model, the analytical expression of vm is derived, showing good agreement with vm in the PIC simulation. However, the oscillation energy in the direction perpendicular to polarization will decrease when electrons are accelerated longitudinally (acceleration damping). As a consequence, the divergence perpendicular to the polarization direction will be smaller. Our research gives a quantitative explanation for the transverse distribution of electrons generated by DLA. With some modification, it can also be used in DLA combined LWFA to better control the dephasing length.-
Keywords:
- direct laser acceleration /
- transverse distribution
[1] Tajima T, Dawson J 1979 Phys. Rev. Lett. 43 267
Google Scholar
[2] Esarey E, Schroeder C B, Leemans W P 2009 Rev. Mod. Phys. 81 1229
Google Scholar
[3] Faure J, Glinec Y, Pukhov A, Kiselev S, Gordienko S, Lefebvre E, Rousseau J P, Burgy F, Malka V 2004 Nature 431 541
Google Scholar
[4] Geddes C, Toth C, van Tilborg J, Esarey E, Schroeder C, Bruhwiler D, Nieter C, Cary J, Leemans W 2004 Nature 431 538
Google Scholar
[5] Mangles S, Murphy C, Najmudin Z, Thomas A, Collier J, Dangor A, Divall E, Foster P, Gallacher J, Hooker C 2004 Nature 431 535
Google Scholar
[6] Lu W, Tzoufras M, Joshi C, Tsung F S, Mori W B, Vieira J, Fonseca R A, Silva L O 2007 Phys. Rev. ST Accel. Beams 10 061301
Google Scholar
[7] Gahn C, Tsakiris G, Pukhov A, Meyer-ter-Vehn J, Pretvyler G, Thirolf P, Habs D, Witte K 1999 Phys. Rev. Lett. 83 4772
Google Scholar
[8] Mangles S P D, Walton B R, Tzoufras M, Najmudin Z, Clarke R J, Dangor A E, Evans R G, Fritzler S, Gopal A, Hernandez-Gomez C, Mori W B, Rozmus W, Tatarakis M, Thomas A G R, Tsung F S, Wei M S, Krushelnick K 2005 Phys. Rev. Lett. 94 245001
Google Scholar
[9] Willingale L, Thomas A G R, Nilson P M, Chen H, Cobble J, Craxton R S, Maksimchuk A, Norreys P A, Sangster T C, Scott R H H, Stoeckl C, Zulick C, Krushelnick K 2013 New J. Phys. 15 025023
Google Scholar
[10] Albert F, Lemos N, Shaw J L, Pollock B B, Goyon C, Schumaker W, Saunders A M, Marsh K A, Pak A, Ralph J E, Martins J L, Amorim L D, Falcone R W, Glenzer S H, Moody J D, Joshi C 2017 Phys. Rev. Lett. 118 134801
Google Scholar
[11] Lemos N, Albert F, Shaw J L, Papp D, Polanek R, King P, Milder A, Marsh K A, Pak A, Pollock B 2018 Plasma Phys. Contr. F. 60
[12] Sarri G, Poder K, Cole J M, Schumaker W, Piazza A D, Reville B, Dzelzainis T, Doria D, Gizzi L A, Grittani G 2015 Nat. Commun. 6 6747
Google Scholar
[13] Ledingham K W D, Mckenna P, Singhal R P 2003 Science 300 1107
Google Scholar
[14] Qi W, Zhang X, Zhang B, He S, Zhang F, Cui B, Yu M, Dai Z, Peng X, Gu Y 2019 Phys. Plasmas 26 043103
Google Scholar
[15] Nilson P M, Mangles S P D, Willingale L, Kaluza M C, Thomas A G R, Tatarakis M, Clarke R J, Lancaster K L, Karsch S, Schreiber J, Najmudin Z, Dangor A E, Krushelnick K 2010 New J. Phys. 12 045014
Google Scholar
[16] Tsakiris G D, Gahn C, Tripathi V K 2000 Phys. Plasmas 7 3017
Google Scholar
[17] Pukhov A, Sheng Z M, Meyer-ter-Vehn J 1999 Phys. Plasmas 6 2847
Google Scholar
[18] Shaw J L, Lemos N, Amorim L D, Vafaei-Najafabadi N, Marsh K A, Tsung F S, Mori W B, Joshi C 2017 Phys. Rev. Lett. 118 064801
Google Scholar
[19] Gallardo González I, Ekerfelt H, Hansson M, Audet T L, Aurand B, Desforges F G, Dufrénoy S D, Persson A, Davoine X, Wahlström C G, Cros B, Lundh O 2018 New J. Phys. 20 053011
Google Scholar
[20] Zhang X, Khudik V N, Shvets G 2015 Phys. Rev. Lett. 114 184801
Google Scholar
[21] Shaw J L, Lemos N, Marsh K A, Froula D H, Joshi C 2018 Plasma Phys. Contr. F. 60 044012
Google Scholar
[22] Fonseca R A, Silva L O, Tsung F S, Decyk V K, Lu W, Ren C, Mori W B, Deng S, Lee S, Katsouleas T 2002 International Conference on Computational Science Amsterdam, The Netherlands, April 21−24, 2002 p342
-
图 1 PIC模拟中
$t = 5965\omega _0^{ - 1}$ 时刻的(a)激光强度包络, (b)电子的电荷密度分布与(c)通道内的聚焦场${E_{\rm{s}}} = {E_{y{\rm{s}}}} - $ $c{B_{z{\rm{s}}}} $ , 模拟中, 等离子体密度为2 × 1019 cm–3, 激光脉宽为0.8 ps, a0 = 3Fig. 1. (a) The laser envelope; (b) electron density; (c) channel focusing force
${E_{\rm{s}}} = {E_{y{\rm{s}}}} - c{B_{z{\rm{s}}}}$ at$t = 5965\omega _0^{ - 1}$ into the simulation, in which the plasma density is 2 × 1019 cm–3 and the laser have a duration 0.8 ps with a0 = 3.
图 2
$t = 5965\omega _0^{ - 1}$ 时刻电子在相空间的分布 (a)电子在能量-vy相空间的分布, 白色虚线是电子横向速度振幅的理论值, 右侧的黑色实线代表着能量大于60 MeV的电子的vy的分布, 为了更好地展示, 其计数值做了归一化处理; (b)能量在60—70 MeV之间的电子在y-py相空间的分布Fig. 2. Electron phase space at
$t = 5965\omega _0^{ - 1}$ : (a) Energy -vy phase space, the white dashed lines denote the amplitude of vy from analytical solution,the black solid line denotes the vy distribution of electrons above 60 MeV, the counts are normalized to achieve a better illustration; (b) the y-py phase space of electrons within energy range from 60 MeV to 70 MeV.
图 3 在
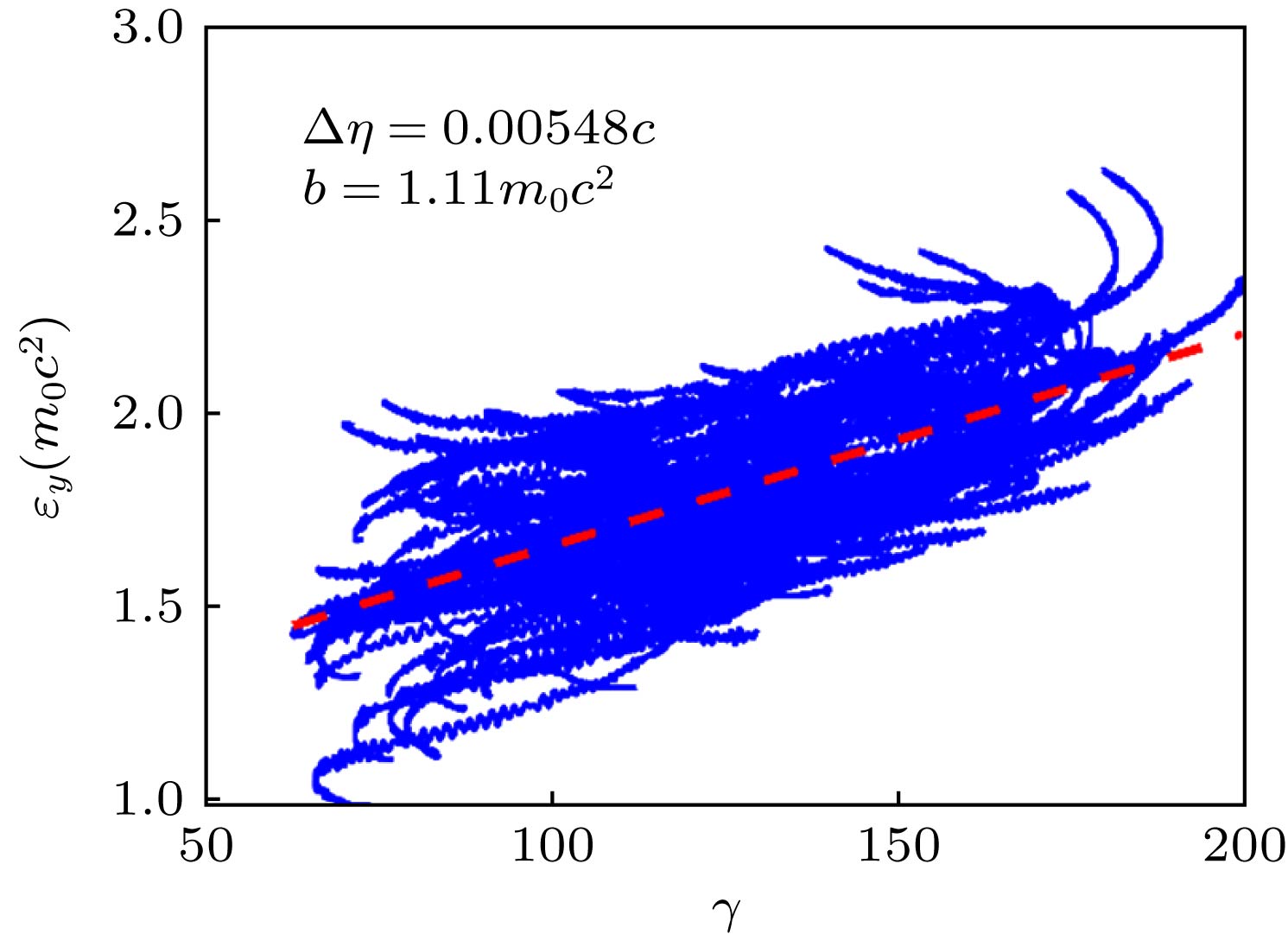
$t = 4965\omega _0^{ - 1}$ 到$t = 6965\omega _0^{ - 1}$ 这段时间内100个被追踪的电子的能量γ以及横向能量${\epsilon_y}$ 的变化, 图中红色实线是根据等式(17)拟合得到的结果Fig. 3. The transverse energy
${\epsilon_y}$ of 100 electrons as a function of γ from$t = 4965\omega _0^{ - 1}$ to$t = 6965\omega _0^{ - 1}$ . The red dashed line is the fitted result according to Eq. (17).
图 4 (a)电子速度振幅
${v_{\rm{m}}}$ 的三种不同展宽; (b)三种展宽下对应的vy的分布Fig. 4. (a) Three distributions of
${v_{\rm{m}}}$ ; (b) the corresponding distributions of vy. -
[1] Tajima T, Dawson J 1979 Phys. Rev. Lett. 43 267
Google Scholar
[2] Esarey E, Schroeder C B, Leemans W P 2009 Rev. Mod. Phys. 81 1229
Google Scholar
[3] Faure J, Glinec Y, Pukhov A, Kiselev S, Gordienko S, Lefebvre E, Rousseau J P, Burgy F, Malka V 2004 Nature 431 541
Google Scholar
[4] Geddes C, Toth C, van Tilborg J, Esarey E, Schroeder C, Bruhwiler D, Nieter C, Cary J, Leemans W 2004 Nature 431 538
Google Scholar
[5] Mangles S, Murphy C, Najmudin Z, Thomas A, Collier J, Dangor A, Divall E, Foster P, Gallacher J, Hooker C 2004 Nature 431 535
Google Scholar
[6] Lu W, Tzoufras M, Joshi C, Tsung F S, Mori W B, Vieira J, Fonseca R A, Silva L O 2007 Phys. Rev. ST Accel. Beams 10 061301
Google Scholar
[7] Gahn C, Tsakiris G, Pukhov A, Meyer-ter-Vehn J, Pretvyler G, Thirolf P, Habs D, Witte K 1999 Phys. Rev. Lett. 83 4772
Google Scholar
[8] Mangles S P D, Walton B R, Tzoufras M, Najmudin Z, Clarke R J, Dangor A E, Evans R G, Fritzler S, Gopal A, Hernandez-Gomez C, Mori W B, Rozmus W, Tatarakis M, Thomas A G R, Tsung F S, Wei M S, Krushelnick K 2005 Phys. Rev. Lett. 94 245001
Google Scholar
[9] Willingale L, Thomas A G R, Nilson P M, Chen H, Cobble J, Craxton R S, Maksimchuk A, Norreys P A, Sangster T C, Scott R H H, Stoeckl C, Zulick C, Krushelnick K 2013 New J. Phys. 15 025023
Google Scholar
[10] Albert F, Lemos N, Shaw J L, Pollock B B, Goyon C, Schumaker W, Saunders A M, Marsh K A, Pak A, Ralph J E, Martins J L, Amorim L D, Falcone R W, Glenzer S H, Moody J D, Joshi C 2017 Phys. Rev. Lett. 118 134801
Google Scholar
[11] Lemos N, Albert F, Shaw J L, Papp D, Polanek R, King P, Milder A, Marsh K A, Pak A, Pollock B 2018 Plasma Phys. Contr. F. 60
[12] Sarri G, Poder K, Cole J M, Schumaker W, Piazza A D, Reville B, Dzelzainis T, Doria D, Gizzi L A, Grittani G 2015 Nat. Commun. 6 6747
Google Scholar
[13] Ledingham K W D, Mckenna P, Singhal R P 2003 Science 300 1107
Google Scholar
[14] Qi W, Zhang X, Zhang B, He S, Zhang F, Cui B, Yu M, Dai Z, Peng X, Gu Y 2019 Phys. Plasmas 26 043103
Google Scholar
[15] Nilson P M, Mangles S P D, Willingale L, Kaluza M C, Thomas A G R, Tatarakis M, Clarke R J, Lancaster K L, Karsch S, Schreiber J, Najmudin Z, Dangor A E, Krushelnick K 2010 New J. Phys. 12 045014
Google Scholar
[16] Tsakiris G D, Gahn C, Tripathi V K 2000 Phys. Plasmas 7 3017
Google Scholar
[17] Pukhov A, Sheng Z M, Meyer-ter-Vehn J 1999 Phys. Plasmas 6 2847
Google Scholar
[18] Shaw J L, Lemos N, Amorim L D, Vafaei-Najafabadi N, Marsh K A, Tsung F S, Mori W B, Joshi C 2017 Phys. Rev. Lett. 118 064801
Google Scholar
[19] Gallardo González I, Ekerfelt H, Hansson M, Audet T L, Aurand B, Desforges F G, Dufrénoy S D, Persson A, Davoine X, Wahlström C G, Cros B, Lundh O 2018 New J. Phys. 20 053011
Google Scholar
[20] Zhang X, Khudik V N, Shvets G 2015 Phys. Rev. Lett. 114 184801
Google Scholar
[21] Shaw J L, Lemos N, Marsh K A, Froula D H, Joshi C 2018 Plasma Phys. Contr. F. 60 044012
Google Scholar
[22] Fonseca R A, Silva L O, Tsung F S, Decyk V K, Lu W, Ren C, Mori W B, Deng S, Lee S, Katsouleas T 2002 International Conference on Computational Science Amsterdam, The Netherlands, April 21−24, 2002 p342
下载:
计量
- 文章访问数: 7503
- PDF下载量: 102
- 被引次数: 0
