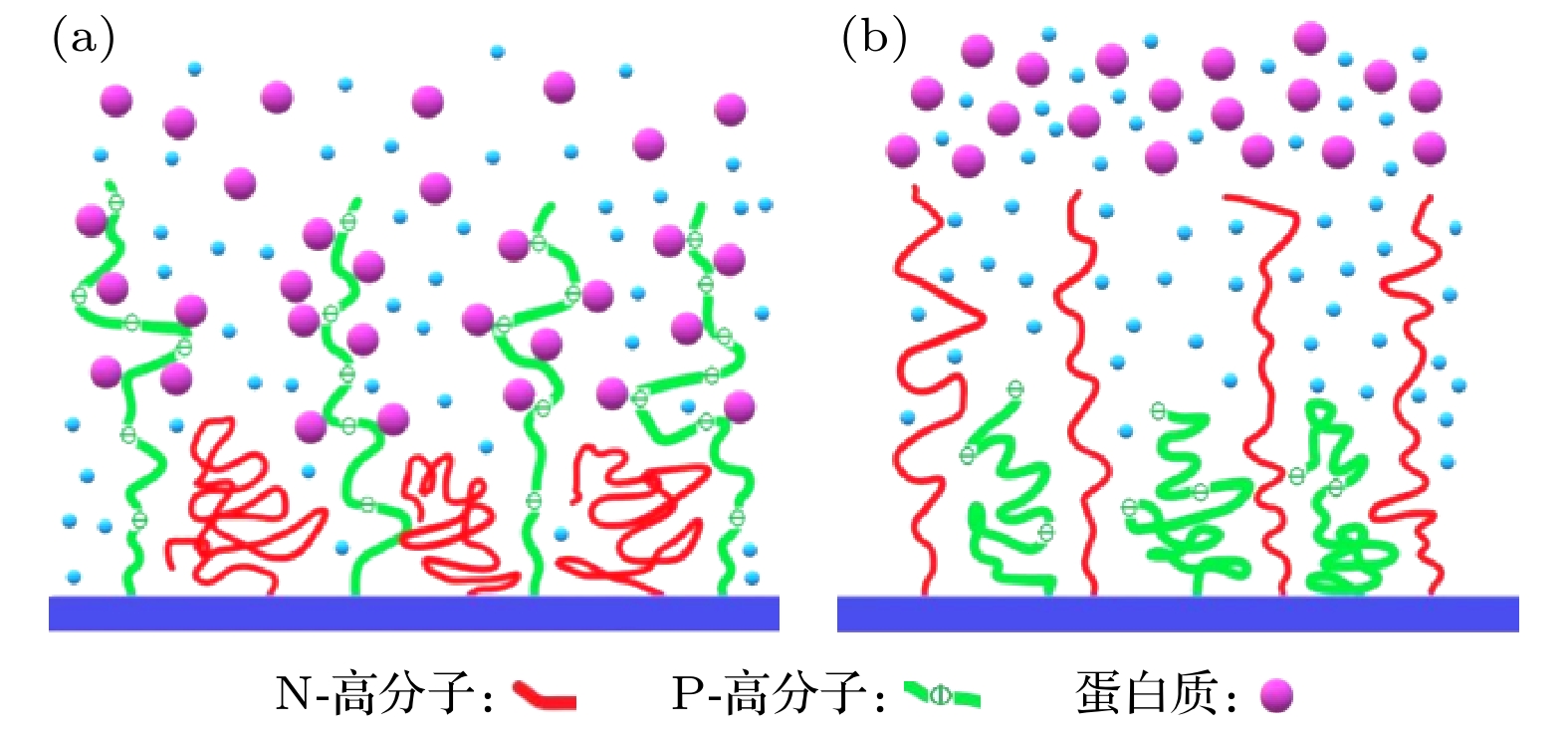
-
本文基于扩散动力学, 建立了一种新的理论模型研究高分子混合刷在蛋白质吸附/脱附过程中的动力学特性. 理论模型考虑高分子混合刷中一种高分子链 (P-高分子链)对蛋白质的吸附, 另一种高分子链 (N-高分子链)对蛋白质的脱附, 以及吸附/脱附的时滞性. 通过选取模型中各参数值, 获得了具有不同化学、物理性质的高分子混合刷对蛋白质的部分吸附/脱附、完全吸附/脱附, 以及周期性吸附/脱附的动力学特性. 研究发现, 由于外加交变电场的作用, 高分子混合刷对蛋白质吸附/脱附过程呈现出周期性循环的动力学特性, 并且平均吸附、脱附量增加. 本文理论结果符合实验观测. 可以预言, 外加交变电场可实现高分子混合刷对蛋白质吸附/脱附的多次循环, 为设计吸附/脱附蛋白质的高分子混合刷纳米材料提供必要的参考和新方案.Based on the diffusion dynamics, a new theoretical model is established to investigate the dynamic properties of a polymer mixed brush (PMB) in the protein adsorption/desorption process. The theoretical model considers the adsorption of proteins by one polymer chain (P-polymer chain) and the desorption of proteins by another polymer chain (N-polymer chain) in a PMB, as well as the time delay between adsorption and desorption. The dynamic properties of protein adsorption/desorption by a PMB depend on not only the chemical and physical properties of polymer chains, but also the microenvironment (density of protein in the solution and protein diffusivity) of the PMB. In order to describe the different chemical and physical properties of polymer chains and microenvironments in PMB, we take different model parameters, and obtain partial adsorption/desorption, complete adsorption/desorption and periodic adsorption/desorption of proteins by the PMB. By analyzing the process of protein adsorption/desorption in a PMB, we find that the microenvironment has an obvious influence on the adsorption and desorption of protein by the PMB. It is also shown that the adsorption of protein and the desorption of protein by the PMB have a stable and invariable periodic cycle when an alternating electric field is applied. The average adsorption capacity and the average desorption capacity increase in comparison with those when no electric field is applied. A stable alternating electric field enables the PMB to exhibit stable periodic dynamic characteristics in the dynamic process of protein adsorption and desorption. Our theoretical results are consistent with the experimental observations. Based on this, it is predicted that an external electric field can realize multiple cycles of protein adsorption and desorption by PMB, which provides necessary references and useful insights into controllable protein adsorption/desorption by the PMB in the practical applications.
-
Keywords:
- polymer mixed brush /
- protein /
- adsorption/desorption /
- dynamic properties
[1] Tan J S, Martic P A 1990 J. Colloid Interf. Sci. 136 415
Google Scholar
[2] Steadman B L, Thompson K C, Middaugh C R, Matsuno K, Vrona S, Lawson E Q, Lewis R V 1992 Biotechn. Bioengin. 40 8
Google Scholar
[3] Norde W, Gage D 2004 Langmuir 20 4162
Google Scholar
[4] Moerz S T, Huber P 2015 J. Phys. Chem. C 119 27072
Google Scholar
[5] Ladam G, Gergely C, Senger B, Decher G, Voegel J C, Schaaf P, Cuisinier F J 2000 Biomacromolecules 1 674
Google Scholar
[6] Wittemann A, Ballauff M 2006 Phys. Chem. Chem. Phys. 8 5269
Google Scholar
[7] Yang J, Hua Z, Wang T, Wu B, Liu G, Zhang G Z 2015 Langmuir 31 6078
Google Scholar
[8] Delcroix M F, Huet G L, Conard T, Demoustier-Champagne S, Prez F E D, Landoulsi J, Dupont-Gillain C C 2013 Biomacromolecules 14 215
Google Scholar
[9] Bratek-Skicki A, Cristaudo V, Savocco J, et al. 2019 Biomacromolecules 20 778
Google Scholar
[10] Pan C, Liu X R, Gong K, Mumtaz F, Wang Y M 2018 J. Mater. Chem. B 6 556
[11] Halperin A 1999 Langmuir 15 2525
Google Scholar
[12] Fang F, Satulovsky J, Szleifer I 2005 Biophys. J. 89 1516
Google Scholar
[13] Su X H, Lei Q L, Ren C L 2015 Chin. Phys. B 24 113601
Google Scholar
[14] Biesheuvel P M, Wittemann A 2005 J. Phys. Chem. B 109 4209
[15] Biesheuvel P M, Leermakers F, Stuart M 2006 Phys. Rev. E 73 011802
[16] Xu Y L, Chen X Q, Chen H Y, Xu S H, Liu H L, Hu Y 2012 Mol. Simulat. 38 274
Google Scholar
[17] Szleifer I, Carignano M A 2000 Macromol. Rapid Commun. 21 423
Google Scholar
[18] Fang F, Szleifer I 2001 Biophys. J. 80 2568
Google Scholar
[19] Fang F, Szleifer I 2002 Langmuir 18 5497
Google Scholar
[20] Weir M P, Heriot S Y, Martin S J, Parnell A J, Holt S A, Webster J R P, Jones R A L 2011 Langmuir 27 11000
Google Scholar
[21] Dunderdale G J, Fairclough J 2013 Langmuir 29 3628
Google Scholar
[22] Lee S J, Park K 1994 J. Vac. Sci. Technol. A 12 2949
Google Scholar
[23] Wittemann A, Ballauff M 2006 Physical Chemistry Chemical Physics 8 5269
[24] Koski J P, Frischknecht A L 2018 ACS Nano. 12 1664
Google Scholar
[25] Russo D, Plazanet M, Teixeira J, Moulin M, Härtlein M, Wurm F R, Steinbach T 2016 Biomacromolecules 17 141
Google Scholar
[26] Feng C, Liu Y, Ren C L 2018 Soft Matter 14 6521
Google Scholar
[27] Hui O, Xia Z, Jiang Z 2009 Nanotechnology 20 195703
Google Scholar
[28] Tong C H 2015 J. Chem. Phys. 143 79
[29] Ding H D, Duan C, Tong C H 2017 J. Chem. Phys. 146 034901
Google Scholar
[30] Baker S L, Murata H, Kaupbayeva B, Tasbolat A, Russell A J 2019 Biomacromolecules 20 2392
Google Scholar
[31] Boubeta F M, Soler-Illia G, Tagliazucchi M 2018 Langmuir 34 15727
Google Scholar
[32] Szleifer I 1997 Phys. A:Statist. Mech. Its Appl. 244 370
Google Scholar
[33] Bratek-Skicki A, Eloy P, Morga M, Dupont-Gillain C 2018 Langmuir 34 3037
Google Scholar
[34] Gong K, Pan C, He K, Zhu H K, Chen L J, Hou M X, Wang Y M 2019 J. Appl. Polym. Sci. 136 48135
Google Scholar
[35] 赵新军, 李九智, 石铭芸, 马超 2019 68 214701
Zhao X J, Li J Z, Shi M Y, M C 2019 Acta Phys. Sin. 68 214701
[36] Ren C L, Ma Y Q 2006 J. Am. Chem. Soc. 128 2733
[37] Mumtaz F, Chen C S, Zhu H K, Pan C, Wang Y M 2018 Appl. Surf. Sci. 439 148
Google Scholar
[38] Delcroix M F, Laurent S, Huet G L, Dupont-Gillain C C 2015 Acta Biomater. 11 68
Google Scholar
-
图 1 高分子混合刷吸附蛋白质和脱附蛋白质系统 (a)吸附; (b)脱附
Fig. 1. Schematic diagrams of adsorption and desorption of protein by a mixed polymer brush: (a) Adsorption; (b) desorption
图 2 高分子混合刷中吸附/脱附的蛋白质分子数密度随时间演化
Fig. 2. The time evolutions of number densities of adsorbed/desorbed proteins in a polymer mixed brush.
图 3 高分子混合刷中完全吸附/脱附蛋白质分子数密度随时间演化
Fig. 3. The time evolutions of number densities of fully adsorbed/desorbed proteins in a polymer mixed brush.
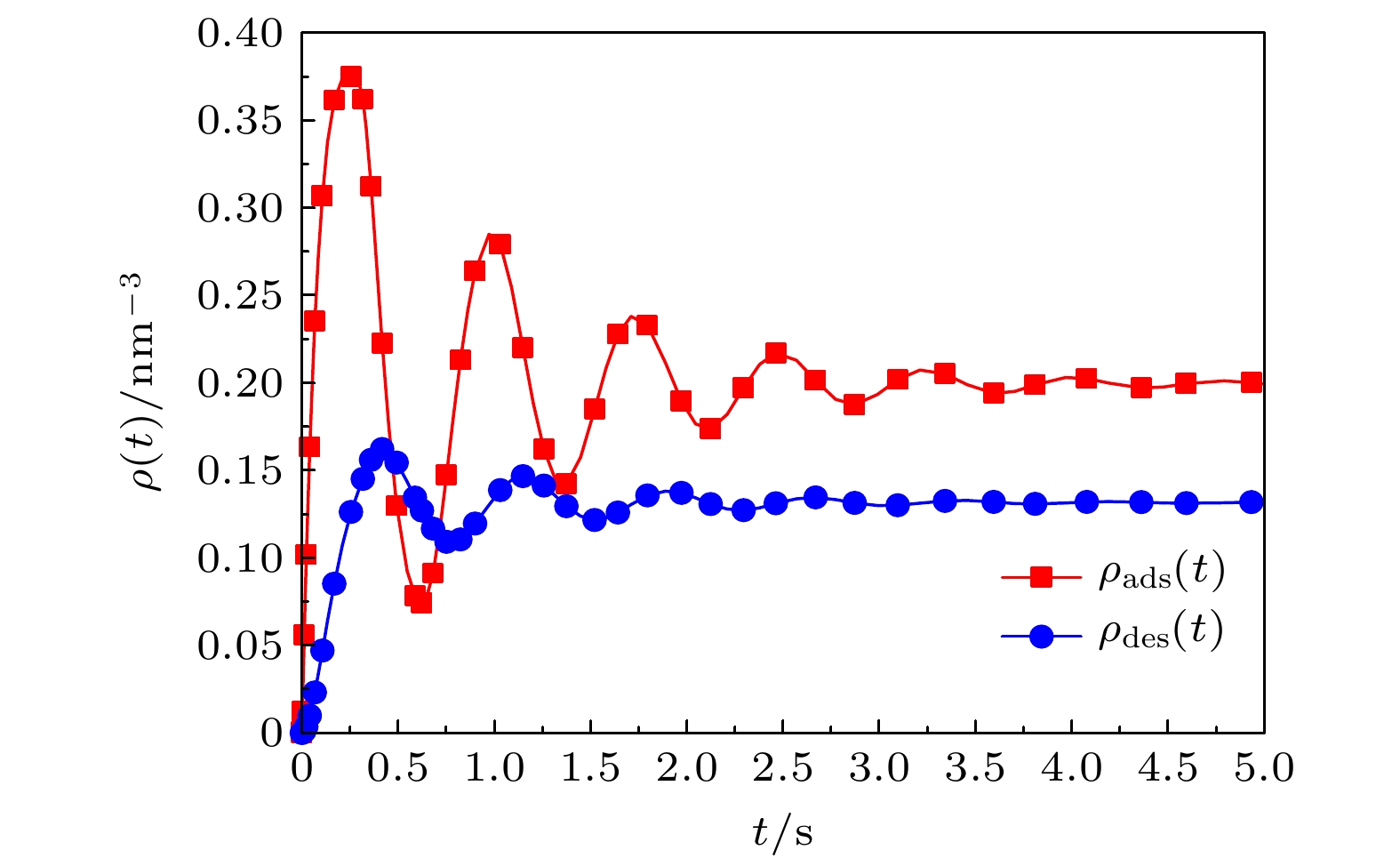
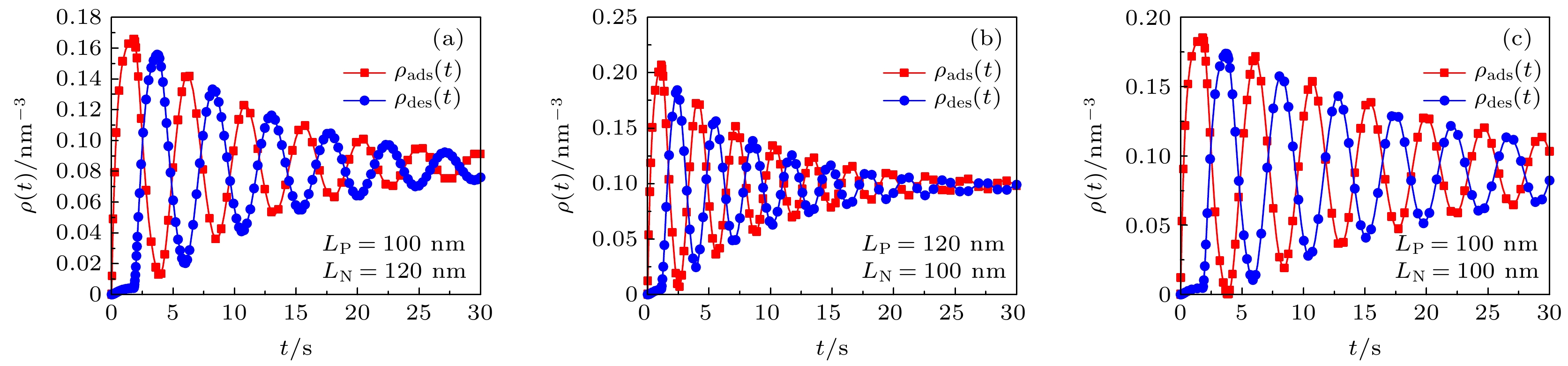
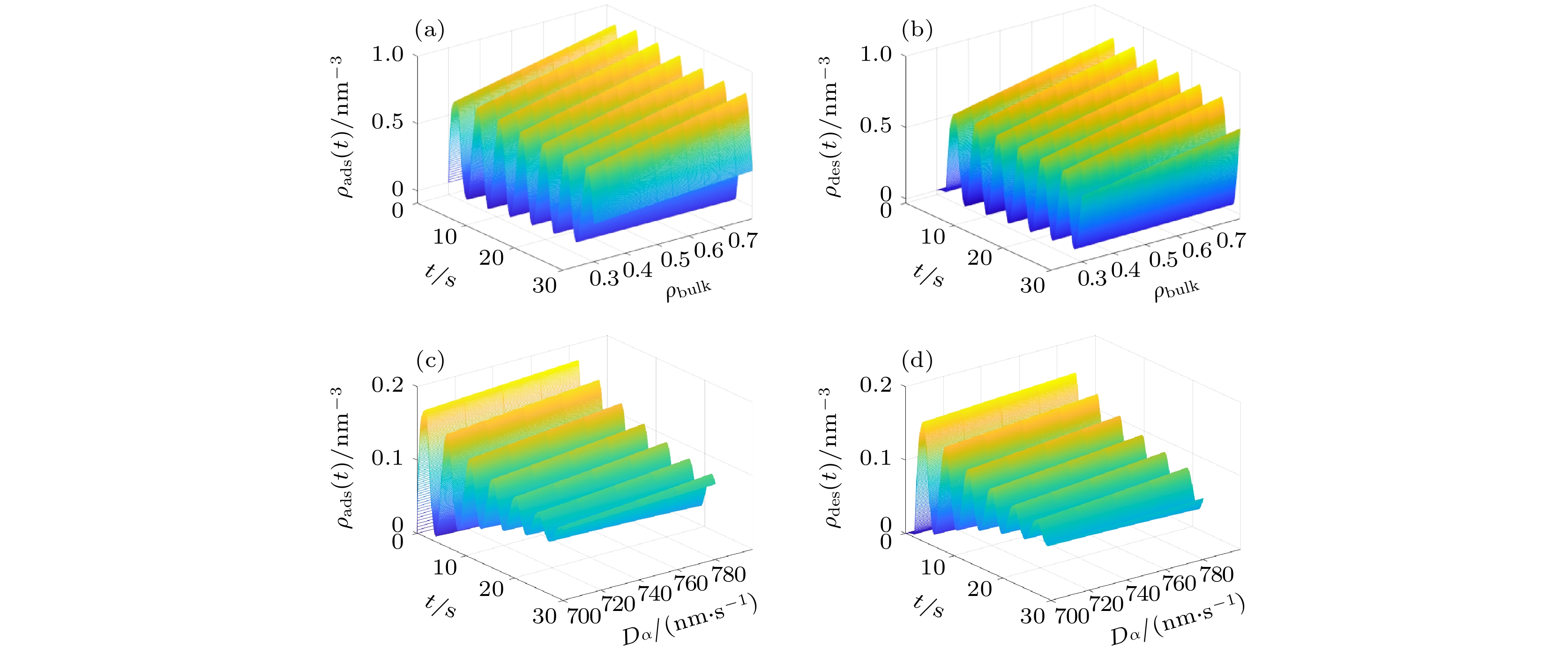
图 4 高分子混合刷中吸附/脱附的蛋白质分子数密度随时间周期性演化关系图. 在子图 (a) 中
$\tau = 1.8\, \, {\rm{s}}$ 、$\tau = 0.3\, \, {\rm{s}}$ ; 在子图 (b)−(e) 中$\tau $ 、$' $ 为变量Fig. 4. The number density of adsorbed/desorbed protein molecules in the polymer mixed brush evolves periodically with time. In subfigure (a),
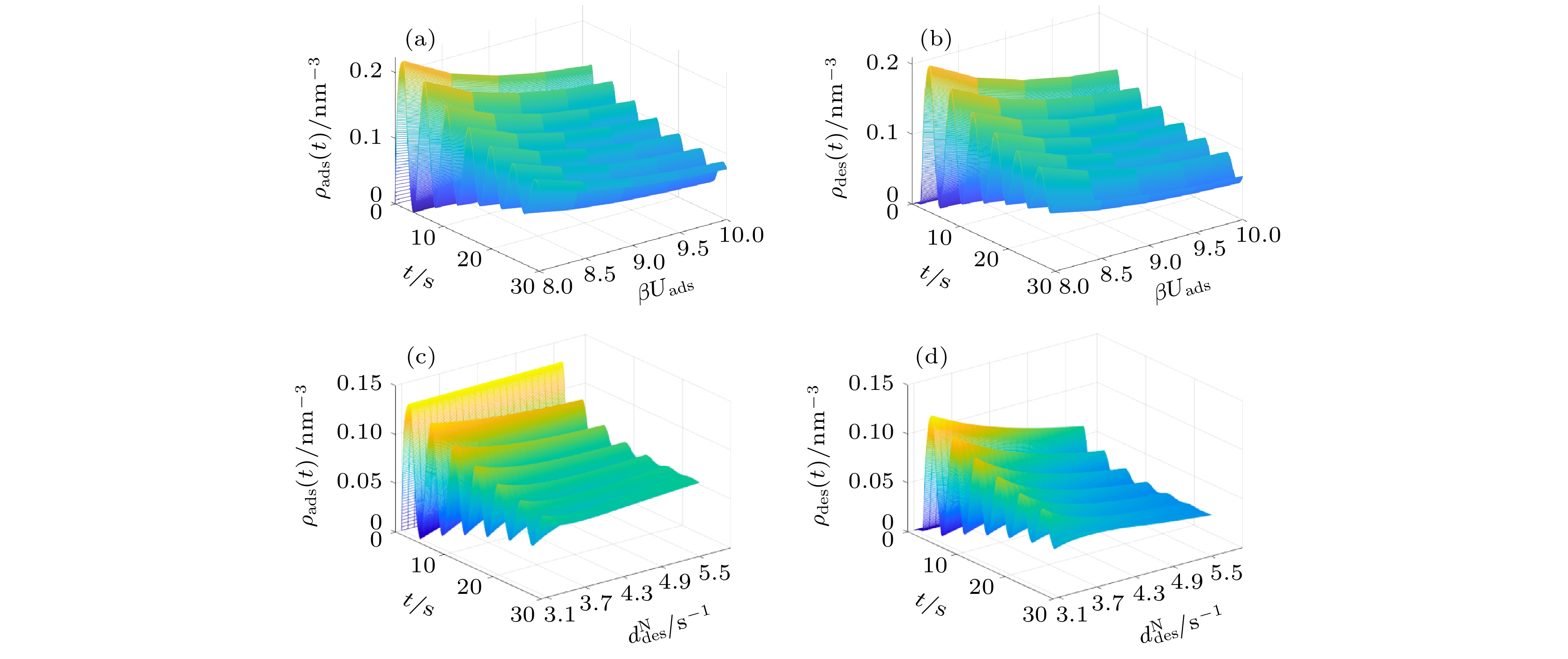
$\tau = 1.8\, \, {\rm{s}}$ 、$\tau = 0.3\, \, {\rm{s}}$ ; in subfigure (b)−(e),$\tau $ and$' $ are variable.
图 5 不同
$\beta {U_{{\rm{ads}}}}$ (a)−(b) 与不同$d_{{\rm{des}}}^{\rm{N}}$ (c)−(d) 条件下, 高分子混合刷中吸附/脱附的蛋白质分子数密度随时间演化的动力学Fig. 5. The dynamics of the number density of adsorbed/desorbed protein molecules by the polymer mixed brush with time evolution at different
$\beta {U_{{\rm{ads}}}}$ (a)−(b) and different$d_{{\rm{des}}}^{\rm{N}}$ (c)−(d).
图 6 在不同链长条件下, 高分子混合刷中吸附/脱附的蛋白质分子数密度随时间周期性演化
Fig. 6. The periodic evolutions of number densities of adsorbed/desorbed proteins in a polymer mixed brush at different chain lengths.
图 7 不同
${\rho _{{\rm{pro, bulk}}}}$ 、${D_\alpha }$ 条件下, 高分子混合刷中吸附/脱附的蛋白质分子数密度随时间演化关系(a)补充分图题说明; (b); (c); (d)Fig. 7. The time evolutions of number densities of adsorbed/desorbed proteins in a polymer mixed brush at different
${\rho _{{\rm{pro, bulk}}}}$ and${D_\alpha }$ : (a); (b); (c); (d).
图 8 在外加电场的条件下，高分子混合刷中吸附/脱附的蛋白质分子数密度随时间演化关系(a)补充分图题说明; (b); (c); (d)
Fig. 8. The time evolutions of number densities of adsorbed/desorbed proteins in a polymer mixed brush when an electric field is applied: (a); (b); (c); (d).
表 1 不同的部分参数所对应的高分子混合刷对蛋白质吸附/解吸附的状态特性
Table 1. The state characteristics of protein adsorption/desorption by polymer mixed brushes corresponding to some different parameters.
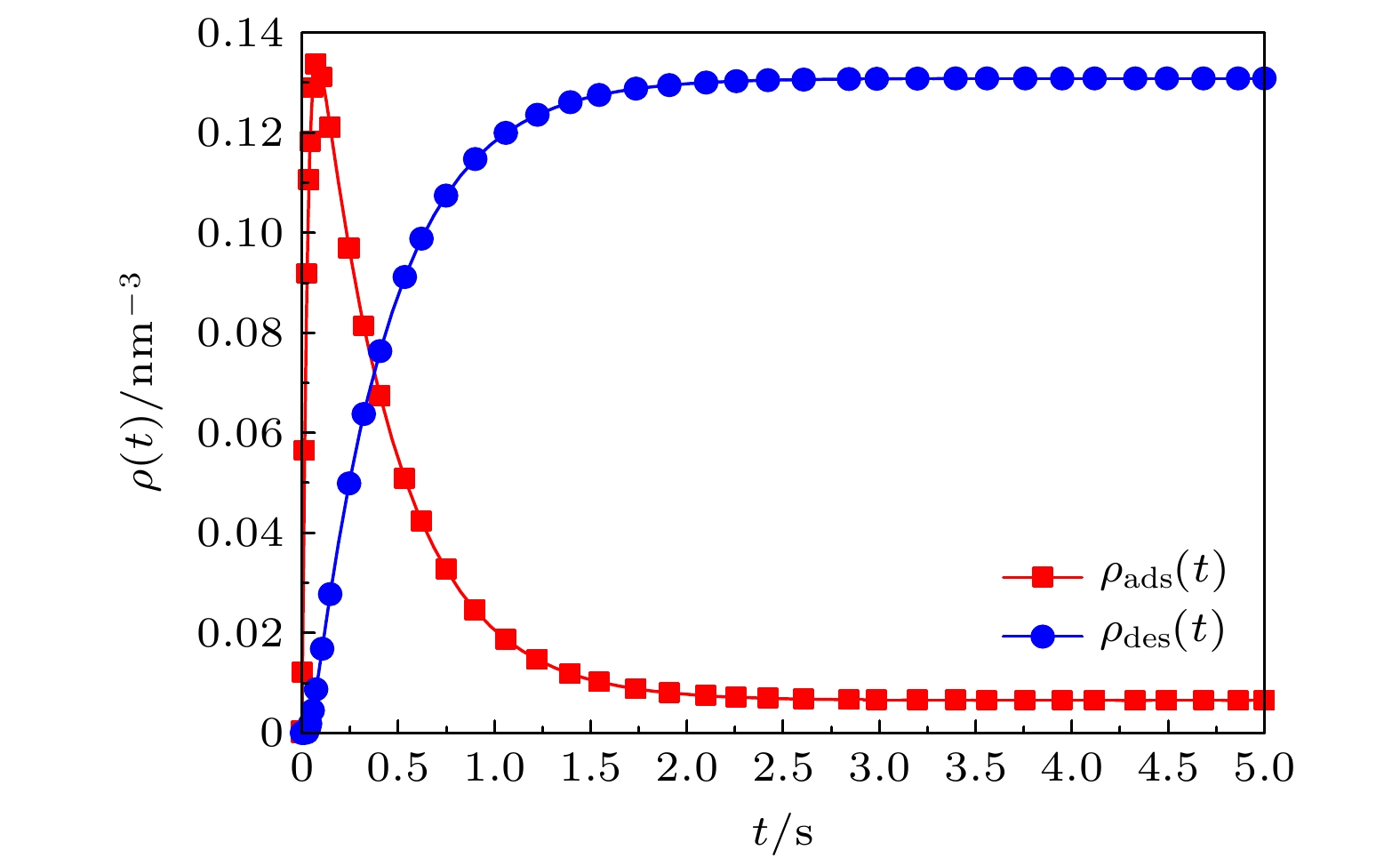
$ {\rho _{{{\rm{pro, bulk}}}}} $ $K_{ { {\rm{des} } } }'/{ { {\rm{s} } }^{ - 1} }$ $ d_{{{\rm{des}}}}^{{\rm{N}}}/{{{\rm{s}}}^{ - 1}} $ $ d_{{{\rm{ads}}}}^{{\rm{P}}}/{{{\rm{s}}}^{ - 1}} $ $ d_{{{\rm{des}}}}^{{\rm{P}}}/{{{\rm{s}}}^{ - 1}} $ $ \tau /{{\rm{s}}} $ $ \tau '/{{\rm{s}}} $ 吸附/脱附特性 $ 0.4 $ $ 0.96\, $ $ 6.0\, $ $ 2.0\, $ $ 3.0\, $ $ 0.3\, $ $ 0.3\, $ 部分吸附/脱附 $ 0.4 $ $ 2.0\, $ $ 0.1 $ $ 27.5\, $ $ 0.01\, $ $ 0.02\, $ $ 0.3\, $ 完全吸附/脱附 $ 0.7 $ $ 2.96\, $ $ 3.1\, $ $ 0.68 $ $ 0.08 $ $ 1.8\, $ $ 0.3\, $ 周期性吸附/脱附 
下载: 导出CSV
-
[1] Tan J S, Martic P A 1990 J. Colloid Interf. Sci. 136 415
Google Scholar
[2] Steadman B L, Thompson K C, Middaugh C R, Matsuno K, Vrona S, Lawson E Q, Lewis R V 1992 Biotechn. Bioengin. 40 8
Google Scholar
[3] Norde W, Gage D 2004 Langmuir 20 4162
Google Scholar
[4] Moerz S T, Huber P 2015 J. Phys. Chem. C 119 27072
Google Scholar
[5] Ladam G, Gergely C, Senger B, Decher G, Voegel J C, Schaaf P, Cuisinier F J 2000 Biomacromolecules 1 674
Google Scholar
[6] Wittemann A, Ballauff M 2006 Phys. Chem. Chem. Phys. 8 5269
Google Scholar
[7] Yang J, Hua Z, Wang T, Wu B, Liu G, Zhang G Z 2015 Langmuir 31 6078
Google Scholar
[8] Delcroix M F, Huet G L, Conard T, Demoustier-Champagne S, Prez F E D, Landoulsi J, Dupont-Gillain C C 2013 Biomacromolecules 14 215
Google Scholar
[9] Bratek-Skicki A, Cristaudo V, Savocco J, et al. 2019 Biomacromolecules 20 778
Google Scholar
[10] Pan C, Liu X R, Gong K, Mumtaz F, Wang Y M 2018 J. Mater. Chem. B 6 556
[11] Halperin A 1999 Langmuir 15 2525
Google Scholar
[12] Fang F, Satulovsky J, Szleifer I 2005 Biophys. J. 89 1516
Google Scholar
[13] Su X H, Lei Q L, Ren C L 2015 Chin. Phys. B 24 113601
Google Scholar
[14] Biesheuvel P M, Wittemann A 2005 J. Phys. Chem. B 109 4209
[15] Biesheuvel P M, Leermakers F, Stuart M 2006 Phys. Rev. E 73 011802
[16] Xu Y L, Chen X Q, Chen H Y, Xu S H, Liu H L, Hu Y 2012 Mol. Simulat. 38 274
Google Scholar
[17] Szleifer I, Carignano M A 2000 Macromol. Rapid Commun. 21 423
Google Scholar
[18] Fang F, Szleifer I 2001 Biophys. J. 80 2568
Google Scholar
[19] Fang F, Szleifer I 2002 Langmuir 18 5497
Google Scholar
[20] Weir M P, Heriot S Y, Martin S J, Parnell A J, Holt S A, Webster J R P, Jones R A L 2011 Langmuir 27 11000
Google Scholar
[21] Dunderdale G J, Fairclough J 2013 Langmuir 29 3628
Google Scholar
[22] Lee S J, Park K 1994 J. Vac. Sci. Technol. A 12 2949
Google Scholar
[23] Wittemann A, Ballauff M 2006 Physical Chemistry Chemical Physics 8 5269
[24] Koski J P, Frischknecht A L 2018 ACS Nano. 12 1664
Google Scholar
[25] Russo D, Plazanet M, Teixeira J, Moulin M, Härtlein M, Wurm F R, Steinbach T 2016 Biomacromolecules 17 141
Google Scholar
[26] Feng C, Liu Y, Ren C L 2018 Soft Matter 14 6521
Google Scholar
[27] Hui O, Xia Z, Jiang Z 2009 Nanotechnology 20 195703
Google Scholar
[28] Tong C H 2015 J. Chem. Phys. 143 79
[29] Ding H D, Duan C, Tong C H 2017 J. Chem. Phys. 146 034901
Google Scholar
[30] Baker S L, Murata H, Kaupbayeva B, Tasbolat A, Russell A J 2019 Biomacromolecules 20 2392
Google Scholar
[31] Boubeta F M, Soler-Illia G, Tagliazucchi M 2018 Langmuir 34 15727
Google Scholar
[32] Szleifer I 1997 Phys. A:Statist. Mech. Its Appl. 244 370
Google Scholar
[33] Bratek-Skicki A, Eloy P, Morga M, Dupont-Gillain C 2018 Langmuir 34 3037
Google Scholar
[34] Gong K, Pan C, He K, Zhu H K, Chen L J, Hou M X, Wang Y M 2019 J. Appl. Polym. Sci. 136 48135
Google Scholar
[35] 赵新军, 李九智, 石铭芸, 马超 2019 68 214701
Zhao X J, Li J Z, Shi M Y, M C 2019 Acta Phys. Sin. 68 214701
[36] Ren C L, Ma Y Q 2006 J. Am. Chem. Soc. 128 2733
[37] Mumtaz F, Chen C S, Zhu H K, Pan C, Wang Y M 2018 Appl. Surf. Sci. 439 148
Google Scholar
[38] Delcroix M F, Laurent S, Huet G L, Dupont-Gillain C C 2015 Acta Biomater. 11 68
Google Scholar
下载:
计量
- 文章访问数: 4725
- PDF下载量: 82
- 被引次数: 0
