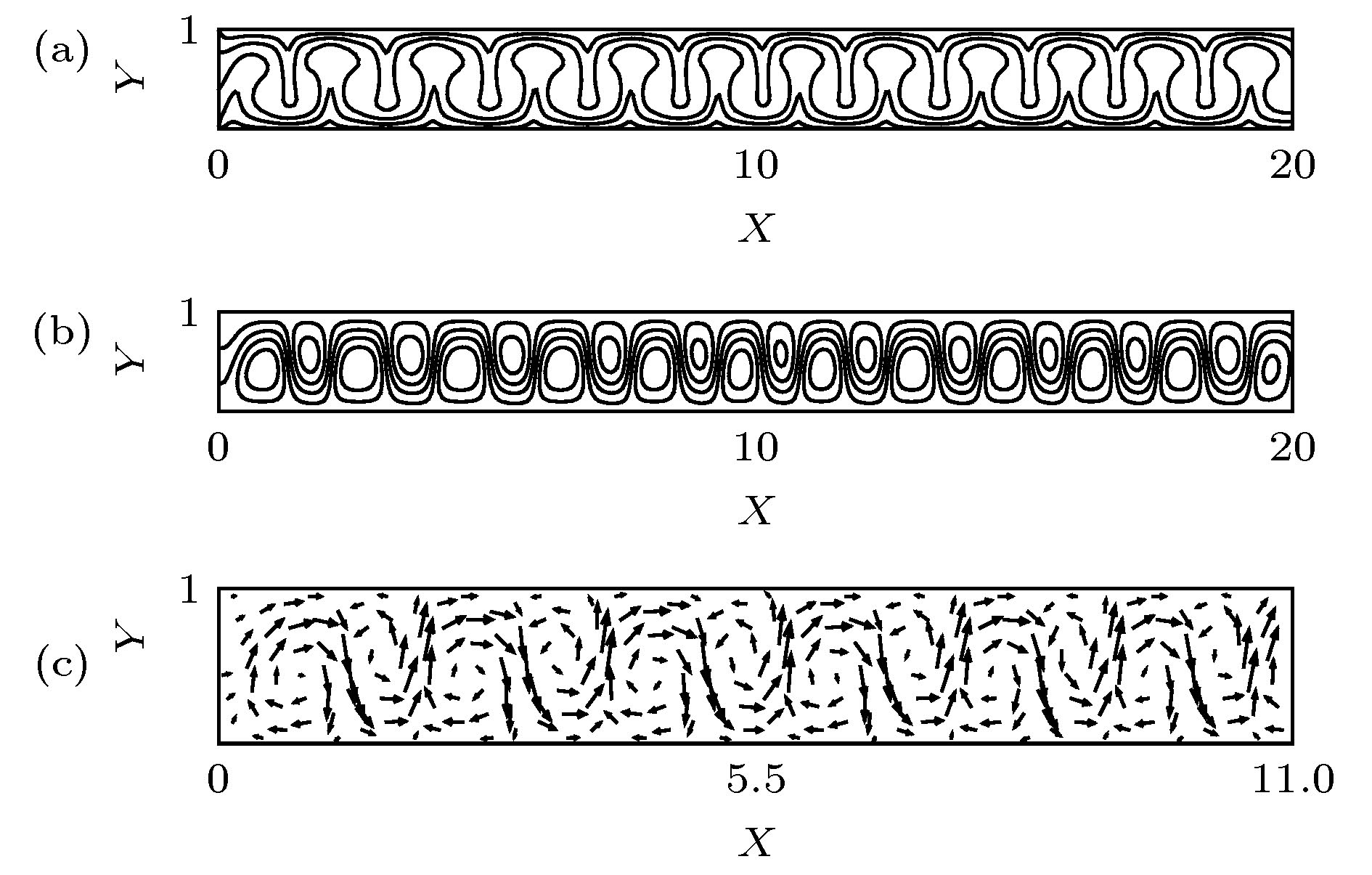
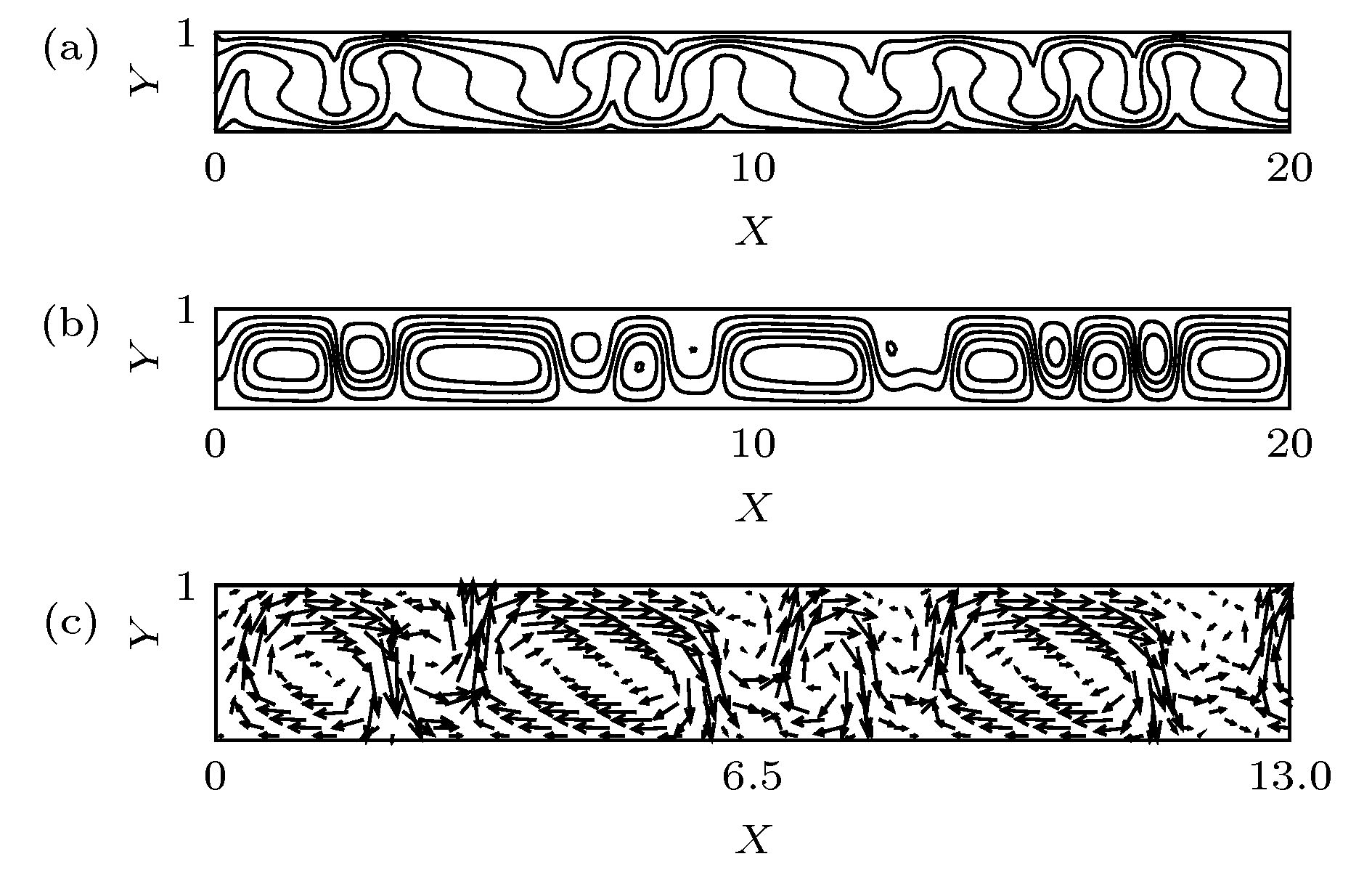
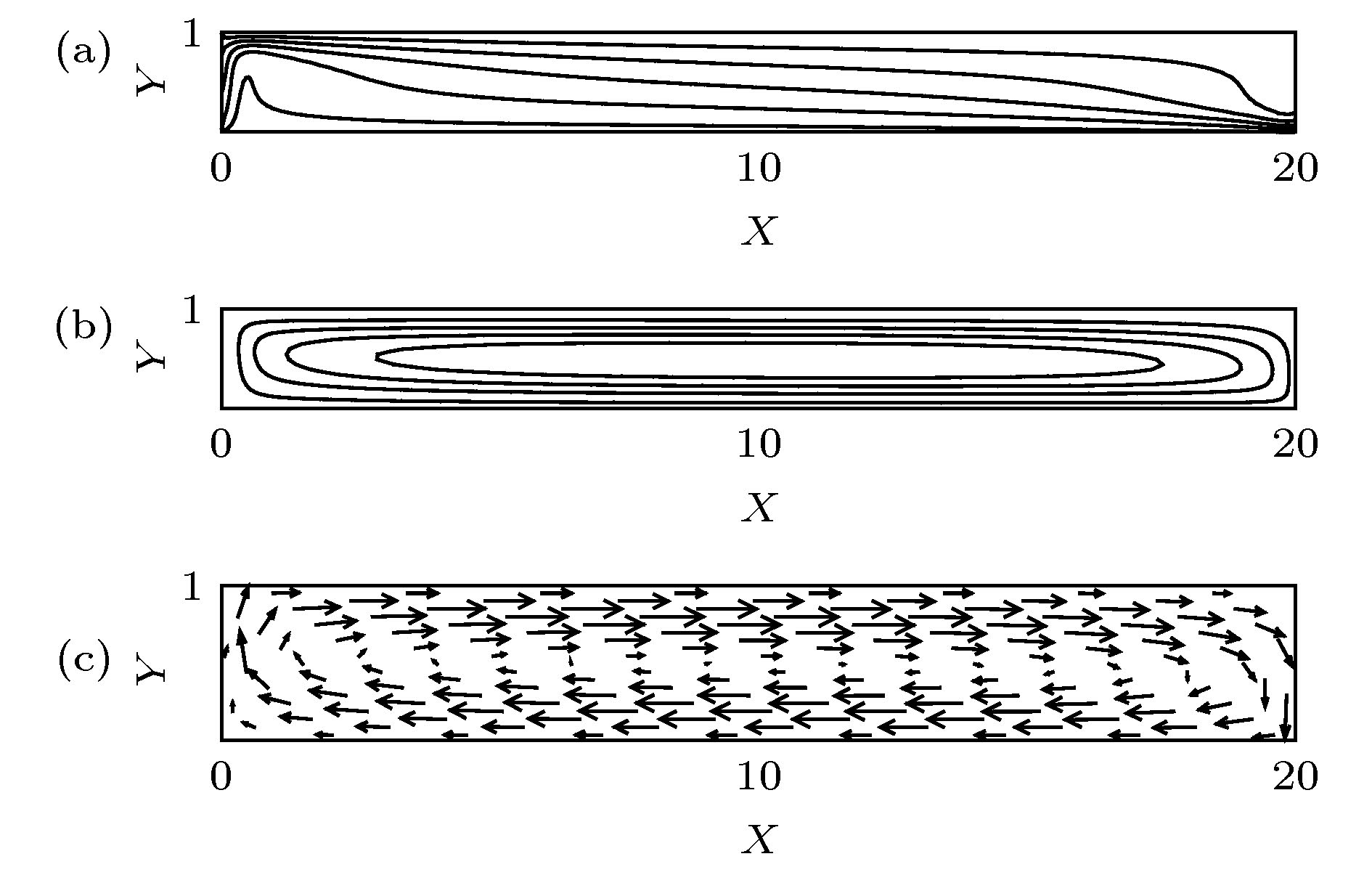
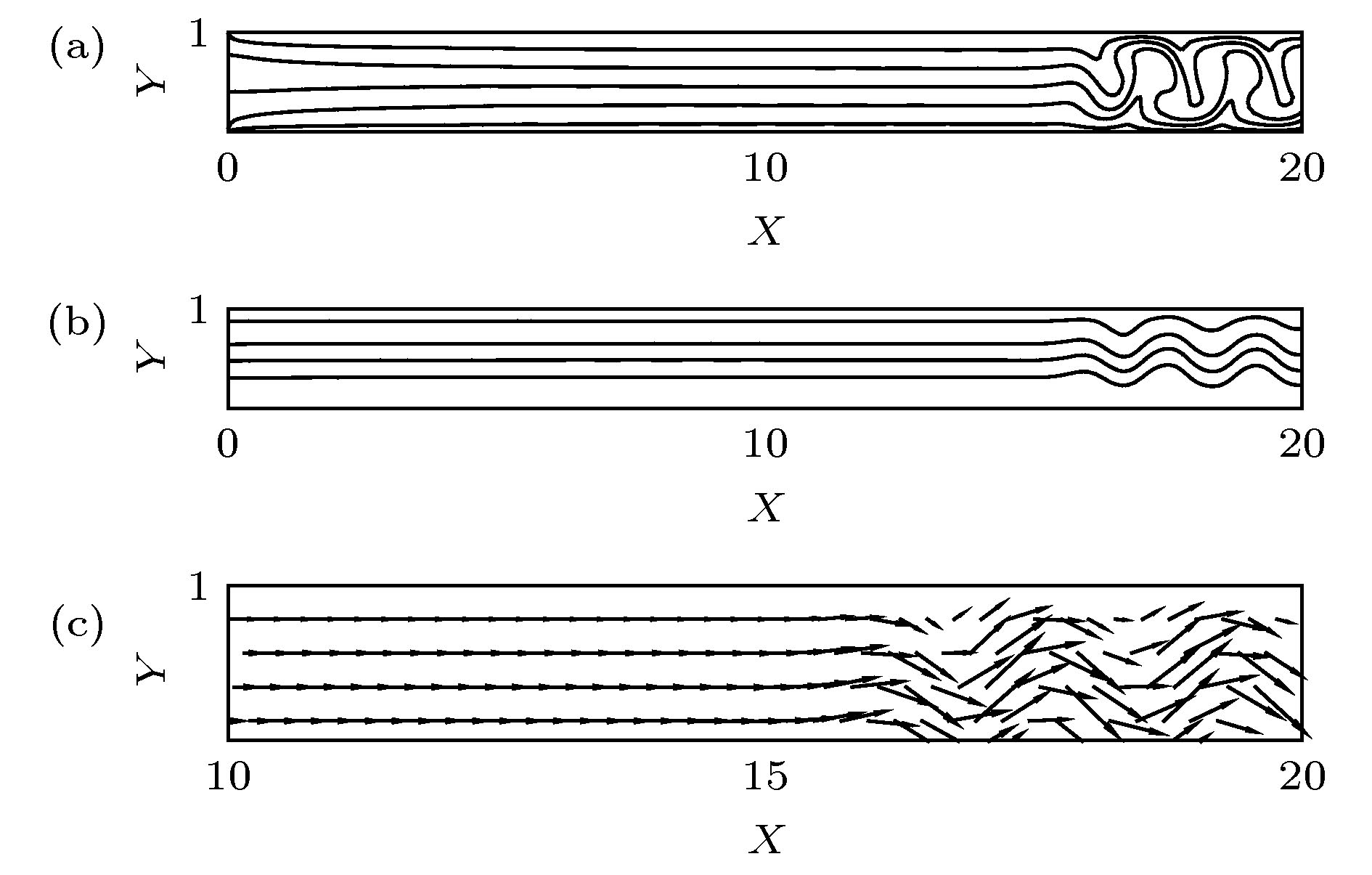
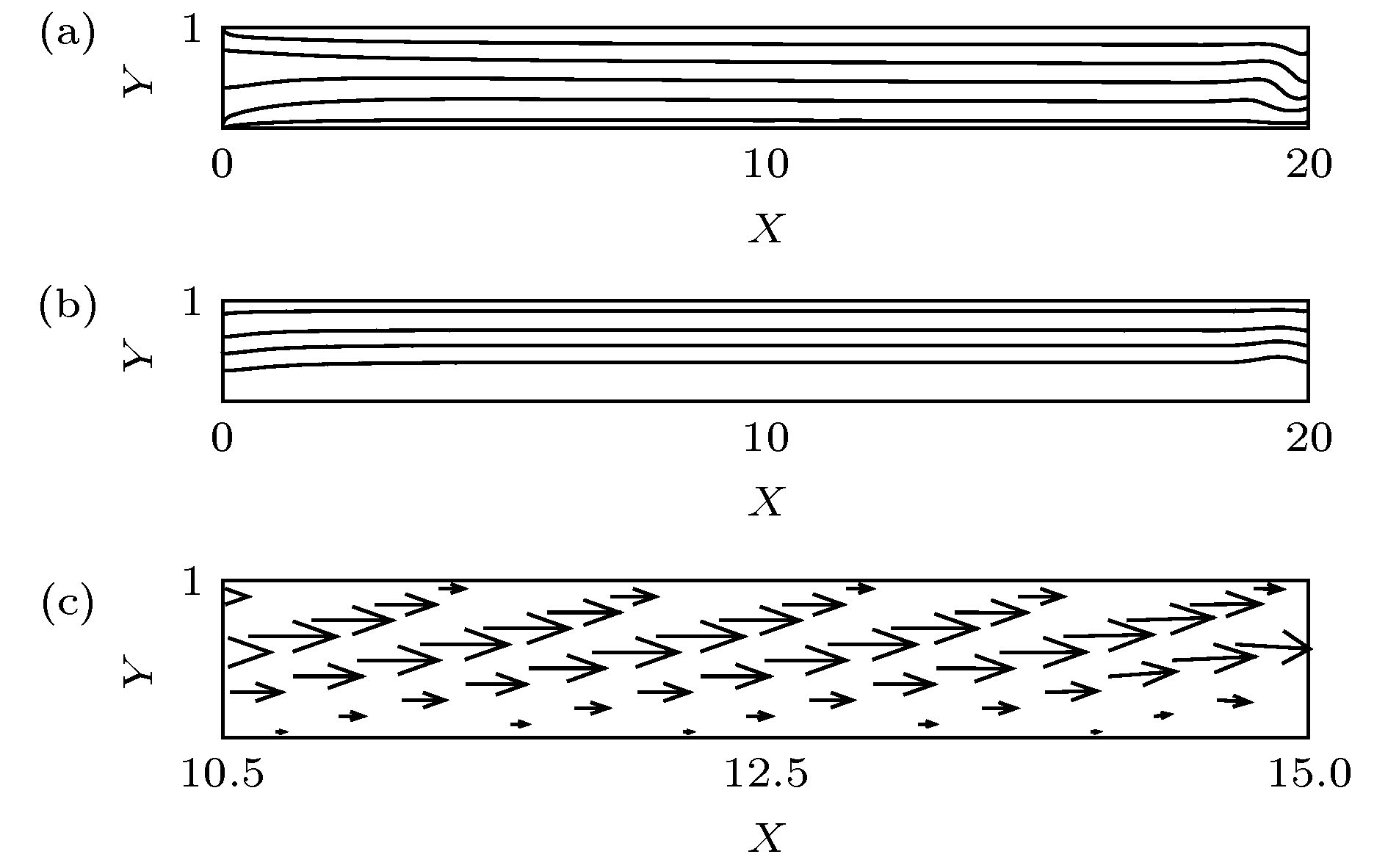
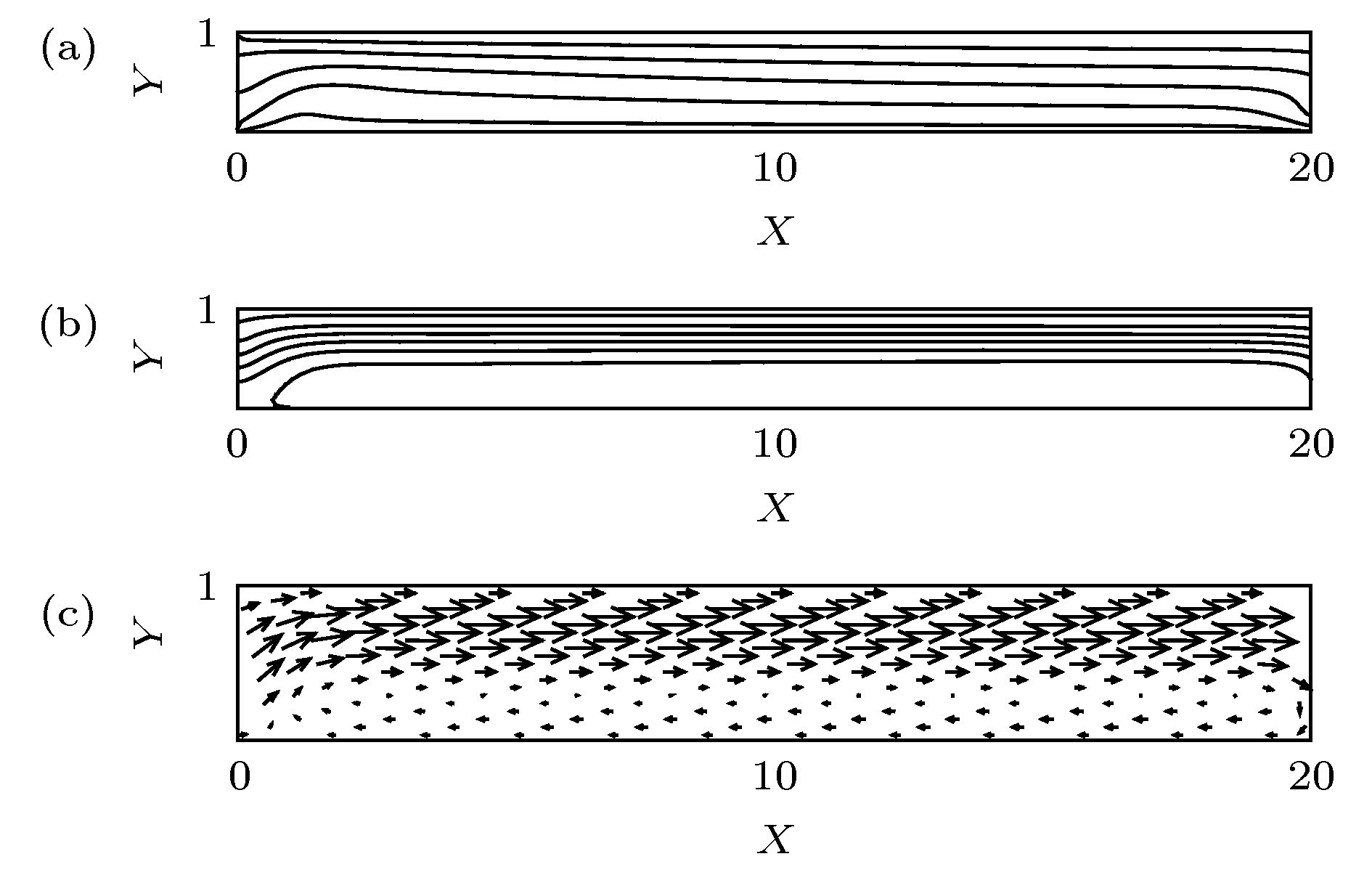
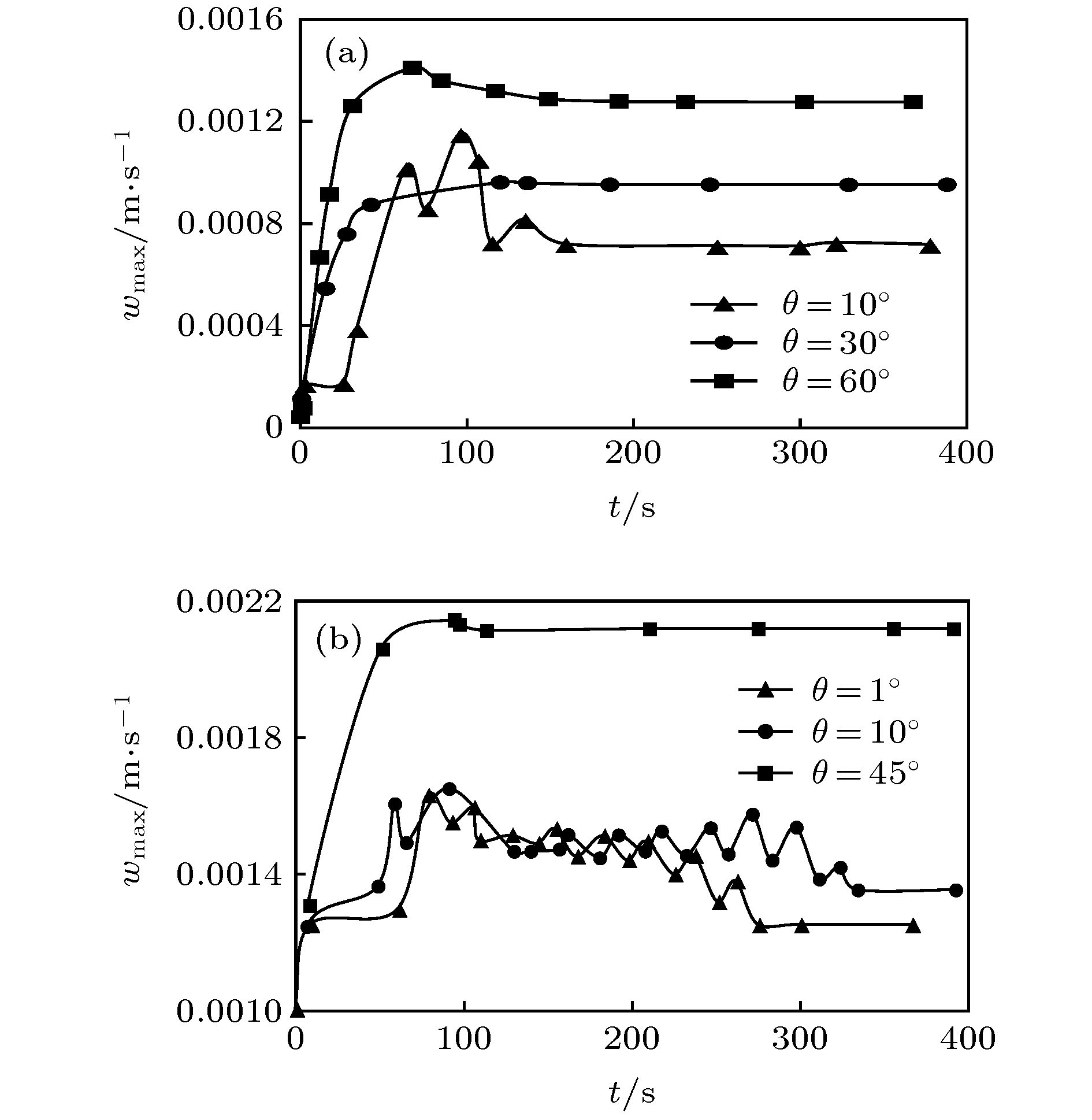
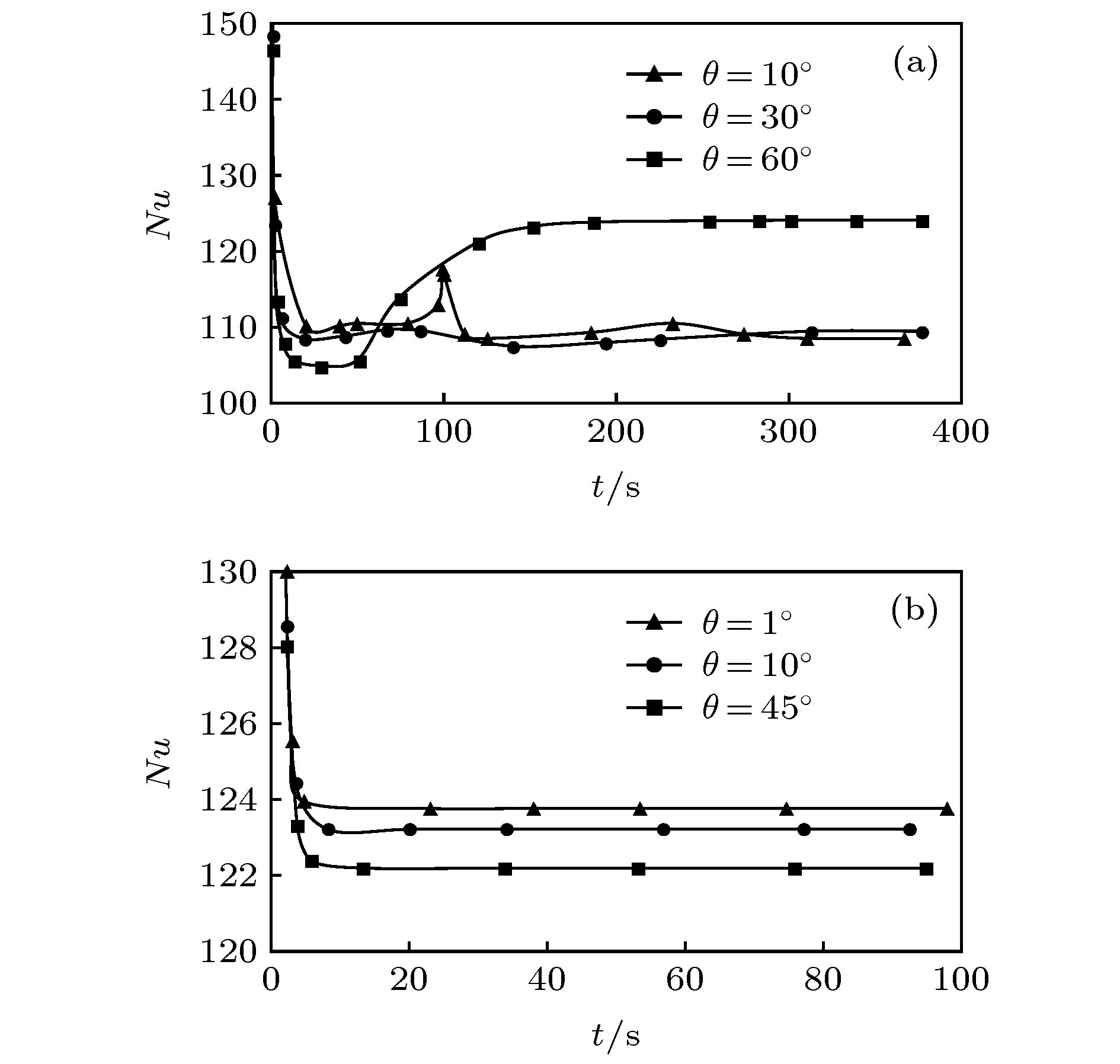
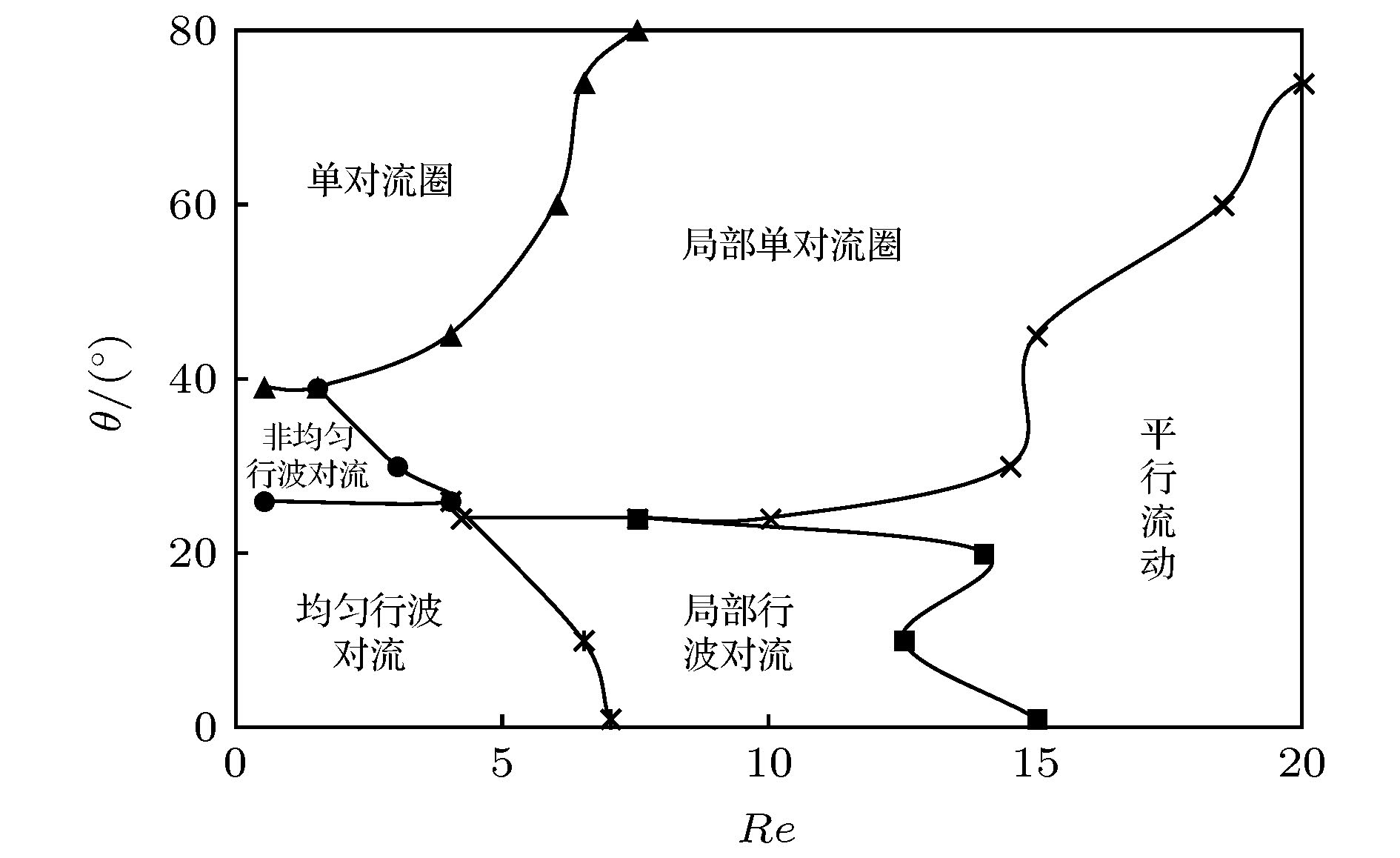
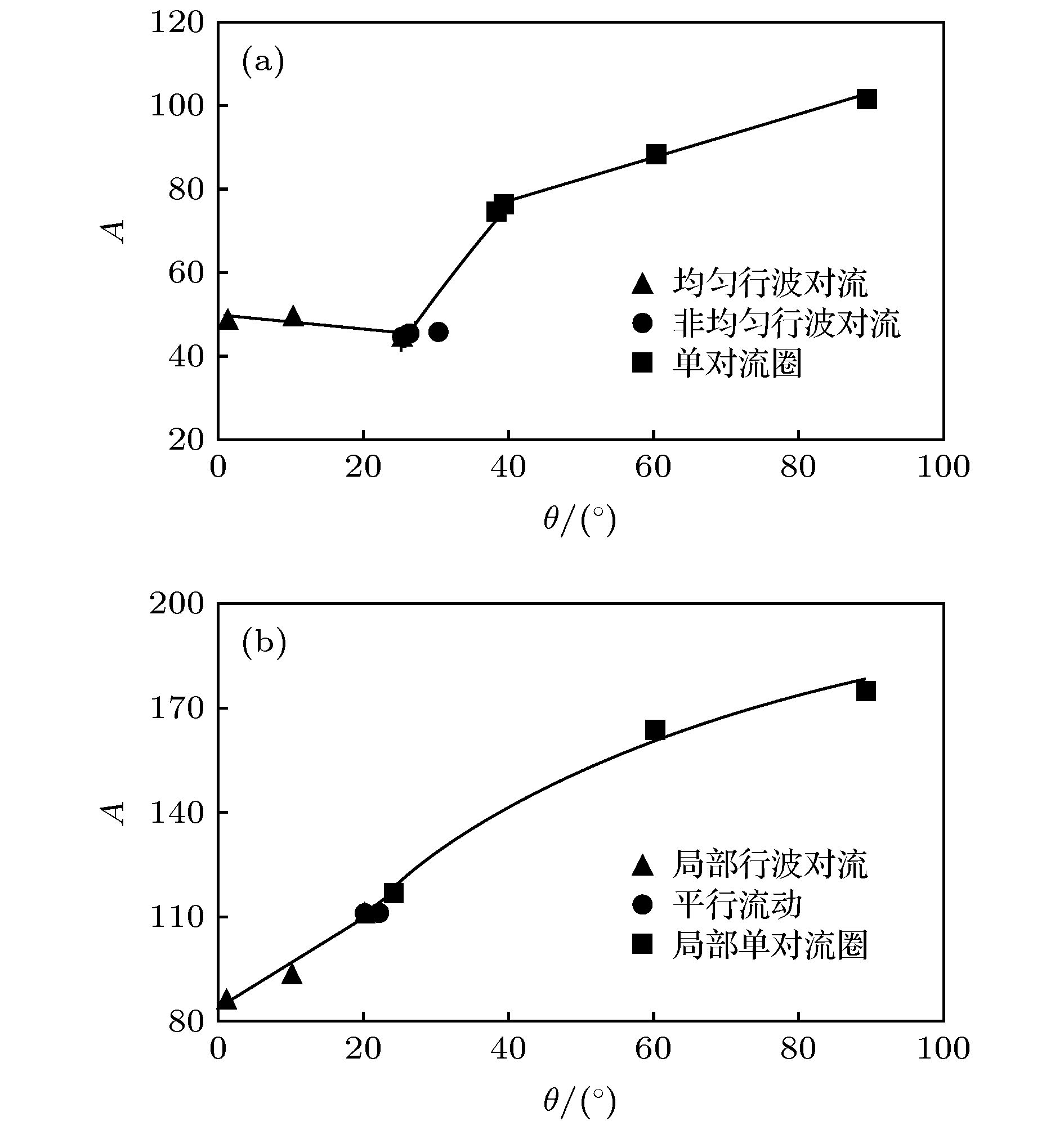
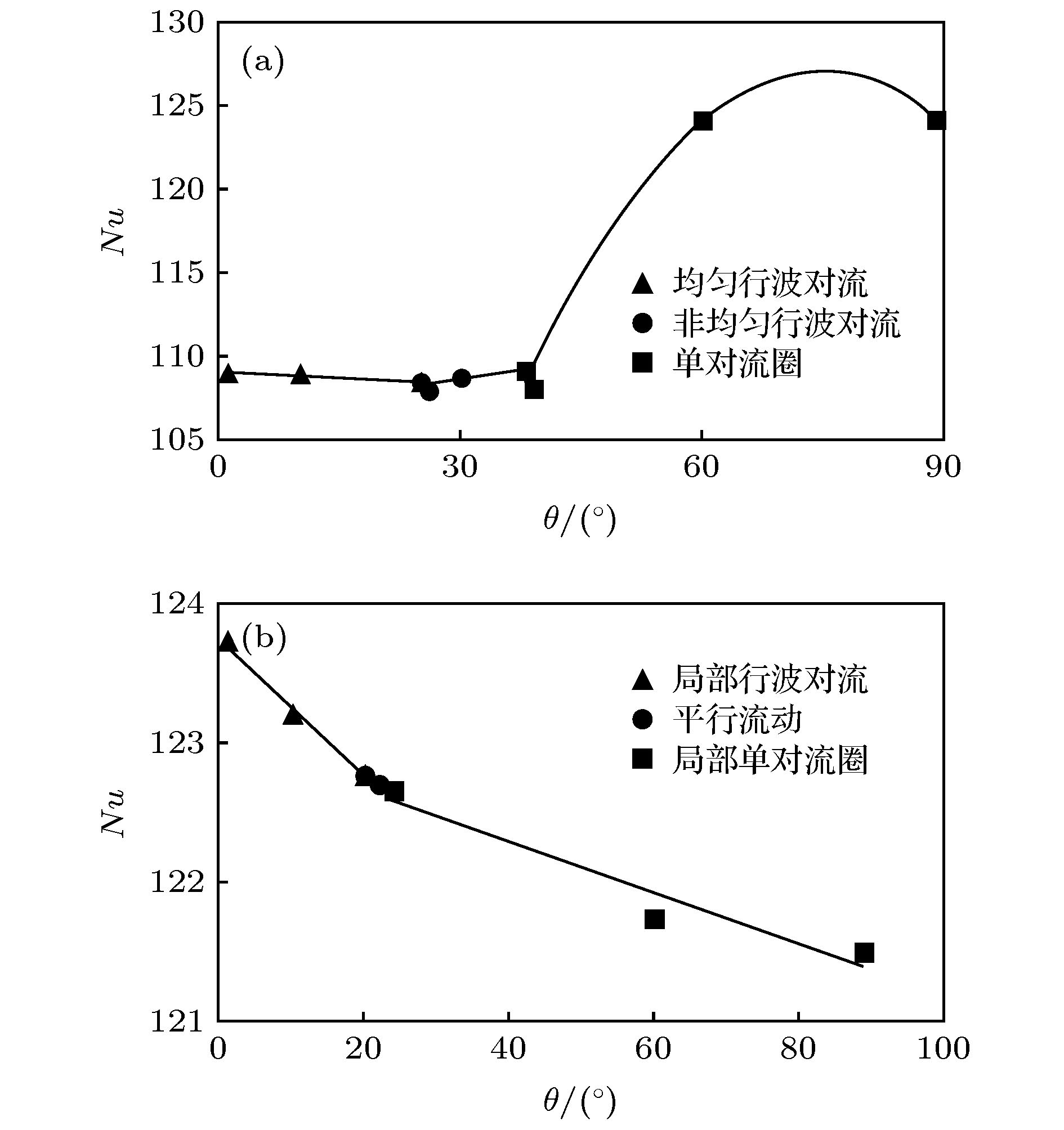
-
利用流体力学基本方程组的数值模拟, 探讨了具有通过流动的倾斜腔体中普朗特数Pr = 6.99的流体的对流分区与动力学特性. 结果表明, 对于相对瑞利数r = 9, 在通过流动雷诺数Re = 1.5时, 随着腔体倾斜角θ的增加, 系统出现均匀行波对流、非均匀行波对流以及单对流圈斑图; 在通过流动雷诺数Re = 12.5时, 随着腔体倾斜角θ的增加, 系统出现局部行波对流、平行流及局部单对流圈斑图; 进一步, 对通过流动雷诺数Re和腔体倾斜角θ的不同组合情况的数值模拟, 发现在通过流动雷诺数Re和腔体倾斜角θ构成的平面上, 具有通过流动的倾斜腔体中的对流可以分成前述六种斑图区域, 即均匀行波对流区、非均匀行波对流区、单对流圈区、局部行波对流区、平行流区及局部单对流圈区. 研究了不同对流区域对流最大垂直流速wmax和努塞尔数Nu随着时间的变化特性. 探讨了不同对流区域对流振幅A和努塞尔数Nu随着腔体倾斜角θ变化的动力学特性.Since Henri Bénard first carried out experiments on convection in the fluid layer heated from below at the beginning of last century, and Lord Rayleigh first analyzed small disturbance theoretically, Rayleigh-Bénard convection has received much attention from many researchers, and has become one of the models to study the spatiotemporal structure, flow stability and dynamic characteristics of convection. The methods of studying the Rayleigh-Bénard convection are divided into experimental research, theoretical analysis and numerical simulation. With the development of computer, the research of numerical simulation has made great progress. Because the Rayleigh-Bénard convection can be accurately described by continuity equation, momentum equation and energy equation of hydrodynamics. Therefore, the numerical simulation based on hydrodynamics equations has aroused a lot of research interest. Based on the classical Rayleigh-Bénard convection, the influence of horizontal flow on the Rayleigh-Bénard convection can be studied by applying horizontal flow to one end of the horizontal cavity. On the other hand, the influence of cavity inclination on Rayleigh-Bénard convection can be studied by considering the variation of inclined angles in the cavity. Some valuable convective properties have been obtained. In order to reveal some new convection structures or phenomena, the effects of cavity inclination and through-flow on Rayleigh-Bénard convection are considered at the same time in this paper.By using the numerical simulation of the basic equations of hydrodynamics, the convection partition and dynamic characteristics of the fluid with Prandtl number Pr = 6.99 in the inclined cavity with through-flows are discussed. The results show that for the reduced Rayleigh number r = 9, the system presents uniform traveling wave convection, non-uniform traveling wave convection and single roll convection pattern at the through-flow Reynolds number Re = 1.5 with the increase of the inclined angle θ in the cavity, that for the through-flow Reynolds number Re = 12.5, the system presents the localized traveling wave convection, parallel flow and localized single roll convection pattern with the increase of the inclined angle θ in the cavity, that furthermore, the numerical simulation of different values of through-flow Reynolds number Re and inclined angle θ in the cavity shows that on the plane composed of through flow Reynolds number Re and inclined angle θ in the cavity, the convection in the inclined cavity with through-flow can be divided into six kinds of pattern regions, namely, uniform traveling wave convection region, non-uniform traveling wave convection region, single roll convection region, localized traveling wave convection region, parallel flow region, and localized single roll convection region. The characteristics of the maximum vertical velocity wmax and Nusselt number Nu of convection varying with time in different convection regions are studied. The dynamic properties of convective amplitude A and Nusselt number Nu in different convective regions varying with inclined angle θ in the cavity are discussed.
-
Keywords:
- through flow /
- inclined cavity /
- convective pattern /
- partition /
- dynamic characteristics
[1] Cross M C, Hohenberg P C 1993 Rev. Mod. Phys. 65 851
[2] Bodenschatz E, Pesch W, Ahlers G 2000 Annu. Rev. Fluid Mech. 32 709
Google Scholar
[3] Watanabe T, Iima M, Nishiura Y 2012 J. Fluid Mech. 712 219
Google Scholar
[4] Mercader I, Batiste O, Alonso A,Knobloch E 2010 Fluid Dyn. Res. 42 025505
Google Scholar
[5] Mercader I, Batiste O, Alonso A, Knobloch E 2013 J. Fluid Mech. 722 240
Google Scholar
[6] 宁利中, 余荔, 袁喆, 周洋 2009 中国科学: 物理学 力学 天文学 39 746
Ning L Z, Yu L, Yuan Z, Zhou Y 2009 Sci. Sin.: Phys. Mech. Astron. 39 746
[7] 宁利中, 王娜, 袁喆, 李开继, 王卓运 2014 63 104401
Google Scholar
Ning L Z, Wang N, Yuan Z, Li K J, Wang Z Y 2014 Acta Phys. Sin. 63 104401
Google Scholar
[8] Barten W, Lucke M, Kamps M, Schmitz R 1995 Phys. Rev. E 51 5662
Google Scholar
[9] Jung D, Lucke M 2002 Phys. Rev. Lett. 89 054502
Google Scholar
[10] Taraut A V, Smorodin B L, Lucke M 2012 New J. Phys. 14 093055
Google Scholar
[11] Mercader I, Batiste O, Alonso A, Knobloch E 2011 J. Fluid Mech. 667 586
Google Scholar
[12] 宁利中, 王永起, 袁喆, 李开继, 胡彪 2016 科学通报 61 872
Google Scholar
Ning L Z, Wang Y Q, Yuan Z, Li K, Hu B 2016 Chin. Sci. Bull. 61 872
Google Scholar
[13] 宁利中, 齐昕, 周洋, 余荔 2009 58 2528
Google Scholar
Ning L Z, Qi X, Zhou Y, Yu L 2009 Acta Phys. Sin. 58 2528
Google Scholar
[14] Zhao B X, Tian Z F 2015 Phys. Fluids 27 074102
Google Scholar
[15] 宁利中, 刘爽, 宁碧波, 袁喆, 田伟利, 渠亚伟 2017 应用力学学报 34 1086
Google Scholar
Ning L Z, Liu S, Ning B B, Yuan Z, Tian W L, Qu Y W 2017 Chin. J. Appl. Mech. 34 1086
Google Scholar
[16] Ning L Z, Qi X, Yuan Z, Shi F 2008 J. Hydrodyn. 20 567
Google Scholar
[17] Jung C, Lucke M, Buchel P 1996 Phys. Rev. E 54 1510
Google Scholar
[18] 胡彪, 宁利中, 宁碧波, 田伟利 2017 科学通报 62 4278
Google Scholar
Hu B, Ning L Z, Ning B B, Tian W L 2017 Chin. Sci. Bull. 62 4278
Google Scholar
[19] 宁利中, 胡彪, 宁碧波, 田伟利 2016 65 214401
Google Scholar
Ning L Z, Hu B, Ning B B, Tian W L 2016 Acta Phys. Sin. 65 214401
Google Scholar
[20] Daniels K E, Bodenschatz E 2002 Phys. Rev. Lett. 88 034501
Google Scholar
[21] Daniels K E, Plappb B, Bodenschatz E 2000 Phys. Rev. Lett. 84 5320
Google Scholar
[22] Daniels K E, Brausch O, Pesch W, Bodenschatz E 2008 J. Fluid Mech. 597 261
Google Scholar
[23] Busse F H, Clever R M 1992 J. Eng. Math 26 1
Google Scholar
[24] 宁利中, 吴昊, 宁碧波, 田伟利, 宁景昊 2019 应用数学和力学 40 398
Google Scholar
Ning L Z, Wu H, Ning B B, Tian W L, Ning J H 2019 Appl. Math. Mech. 40 398
Google Scholar
[25] 宁利中, 张珂, 宁碧波, 吴昊, 田伟利 2020 应用力学学报 37 737
Google Scholar
Ning L Z, Zhang K, Ning B B, Wu H, Tian W L 2020 Chin. J. Appl. Mech. 37 737
Google Scholar
[26] Patankar S V 1982 Computation of Heat Transfer and Fluid Flow (Minneapolis: University of Minnesota) pp20−30
[27] 胡彪, 宁利中, 宁碧波, 田伟利, 吴昊, 宁景昊 2017 水动力学研究与进展 32 336
Google Scholar
Hu B, Ning L Z, Ning B B, Tian W L, Wu H, Ning J H 2017 Chin. J. Hydrodyn. 32 336
Google Scholar
-
图 2
${{Re}} = 1.5$ 且${{\theta }} = 10^\circ $ 时的均匀行波对流 (a) 温度; (b)流线; (c)速度矢量Fig. 2. Uniform traveling wave convection at
${{Re}} = 1.5$ and${{\theta }} = 10^\circ $ : (a) Temperature; (b) streamlines; (c) velocity vector
图 3
${{Re}} = 1.5$ 和${{\theta }} = 30^\circ $ 时的非均匀行波对流 (a) 温度; (b)流线; (c)速度矢量Fig. 3. Non-uniform traveling wave convection at
${{Re}} = 1.5$ and${{\theta }} = 30^\circ $ : (a) Temperature; (b) streamlines; (c) velocity vector
图 4
${{Re}} = 1.5$ 和${{\theta }} = 60^\circ $ 时的单对流圈 (a) 温度; (b)流线; (c)速度矢量Fig. 4. Single roll convection at
${{Re}} = 1.5$ and${{\theta }} = 60^\circ $ : (a) Temperature; (b) streamlines; (c) velocity vector.
图 5
${{Re}} = 12.5$ 和${{\theta }} = 1^\circ $ 时的局部行波对流 (a) 温度; (b)流线; (c)速度矢量Fig. 5. Localized traveling wave convection at
${{Re}} = 12.5$ and${{\theta }} = 1^\circ $ : (a) Temperature; (b) streamlines; (c) velocity vector.
图 6
${{Re}} = 12.5$ 和${{\theta }} = 10^\circ $ 时的平行流动 (a) 温度; (b)流线; (c)速度矢量Fig. 6. Parallel flows at
${{Re}} = 12.5$ and${{\theta }} = 10^\circ $ : (a) Temperature; (b) streamlines; (c) velocity vector.
图 7
$R{{e}} = 12.5$ 和${{\theta }} = 45^\circ $ 时的局部单对流圈 (a) 温度; (b)流线; (c)速度矢量Fig. 7. Localized single roll convection at
$R{{e}} = 12.5$ and${{\theta }} = 45^\circ $ : (a) Temperature; (b) streamlines; (c) velocity vector.
图 8 不同对流结构的最大垂直流速的时间演化 (a) Re = 1.5; (b) Re = 12.5
Fig. 8. Time evolution of maximum vertical velocity in different convection structures: (a) Re = 1.5; (b) Re = 12.5.
图 9 不同对流结构的努塞尔数的时间演化 (a) Re = 1.5; (b) Re = 12.5
Fig. 9. Time evolution of Nusselt number in different convection structures: (a) Re = 1.5; (b) Re = 12.5.
图 10 不同对流斑图在倾斜角度
$\theta $ -雷诺数${{Re}}$ 平面上的分区Fig. 10. Partition of different convective patterns in the plane
$\theta $ -${{Re}}$ .
图 11 不同对流结构时A随着
${{\theta }}$ 的变化 (a) Re = 1.5; (b) Re = 12.5Fig. 11. Variation of A in different convection structures with
${{\theta }}$ : (a) Re = 1.5; (b) Re = 12.5.
图 12 不同对流结构时
${{Nu}}$ 随着${{\theta }}$ 的变化 (a) Re = 1.5; (b) Re = 12.5Fig. 12. Variation of
${{Nu}}$ in different convection structures with${{\theta }}$ : (a) Re = 1.5; (b) Re = 12.5. -
[1] Cross M C, Hohenberg P C 1993 Rev. Mod. Phys. 65 851
[2] Bodenschatz E, Pesch W, Ahlers G 2000 Annu. Rev. Fluid Mech. 32 709
Google Scholar
[3] Watanabe T, Iima M, Nishiura Y 2012 J. Fluid Mech. 712 219
Google Scholar
[4] Mercader I, Batiste O, Alonso A,Knobloch E 2010 Fluid Dyn. Res. 42 025505
Google Scholar
[5] Mercader I, Batiste O, Alonso A, Knobloch E 2013 J. Fluid Mech. 722 240
Google Scholar
[6] 宁利中, 余荔, 袁喆, 周洋 2009 中国科学: 物理学 力学 天文学 39 746
Ning L Z, Yu L, Yuan Z, Zhou Y 2009 Sci. Sin.: Phys. Mech. Astron. 39 746
[7] 宁利中, 王娜, 袁喆, 李开继, 王卓运 2014 63 104401
Google Scholar
Ning L Z, Wang N, Yuan Z, Li K J, Wang Z Y 2014 Acta Phys. Sin. 63 104401
Google Scholar
[8] Barten W, Lucke M, Kamps M, Schmitz R 1995 Phys. Rev. E 51 5662
Google Scholar
[9] Jung D, Lucke M 2002 Phys. Rev. Lett. 89 054502
Google Scholar
[10] Taraut A V, Smorodin B L, Lucke M 2012 New J. Phys. 14 093055
Google Scholar
[11] Mercader I, Batiste O, Alonso A, Knobloch E 2011 J. Fluid Mech. 667 586
Google Scholar
[12] 宁利中, 王永起, 袁喆, 李开继, 胡彪 2016 科学通报 61 872
Google Scholar
Ning L Z, Wang Y Q, Yuan Z, Li K, Hu B 2016 Chin. Sci. Bull. 61 872
Google Scholar
[13] 宁利中, 齐昕, 周洋, 余荔 2009 58 2528
Google Scholar
Ning L Z, Qi X, Zhou Y, Yu L 2009 Acta Phys. Sin. 58 2528
Google Scholar
[14] Zhao B X, Tian Z F 2015 Phys. Fluids 27 074102
Google Scholar
[15] 宁利中, 刘爽, 宁碧波, 袁喆, 田伟利, 渠亚伟 2017 应用力学学报 34 1086
Google Scholar
Ning L Z, Liu S, Ning B B, Yuan Z, Tian W L, Qu Y W 2017 Chin. J. Appl. Mech. 34 1086
Google Scholar
[16] Ning L Z, Qi X, Yuan Z, Shi F 2008 J. Hydrodyn. 20 567
Google Scholar
[17] Jung C, Lucke M, Buchel P 1996 Phys. Rev. E 54 1510
Google Scholar
[18] 胡彪, 宁利中, 宁碧波, 田伟利 2017 科学通报 62 4278
Google Scholar
Hu B, Ning L Z, Ning B B, Tian W L 2017 Chin. Sci. Bull. 62 4278
Google Scholar
[19] 宁利中, 胡彪, 宁碧波, 田伟利 2016 65 214401
Google Scholar
Ning L Z, Hu B, Ning B B, Tian W L 2016 Acta Phys. Sin. 65 214401
Google Scholar
[20] Daniels K E, Bodenschatz E 2002 Phys. Rev. Lett. 88 034501
Google Scholar
[21] Daniels K E, Plappb B, Bodenschatz E 2000 Phys. Rev. Lett. 84 5320
Google Scholar
[22] Daniels K E, Brausch O, Pesch W, Bodenschatz E 2008 J. Fluid Mech. 597 261
Google Scholar
[23] Busse F H, Clever R M 1992 J. Eng. Math 26 1
Google Scholar
[24] 宁利中, 吴昊, 宁碧波, 田伟利, 宁景昊 2019 应用数学和力学 40 398
Google Scholar
Ning L Z, Wu H, Ning B B, Tian W L, Ning J H 2019 Appl. Math. Mech. 40 398
Google Scholar
[25] 宁利中, 张珂, 宁碧波, 吴昊, 田伟利 2020 应用力学学报 37 737
Google Scholar
Ning L Z, Zhang K, Ning B B, Wu H, Tian W L 2020 Chin. J. Appl. Mech. 37 737
Google Scholar
[26] Patankar S V 1982 Computation of Heat Transfer and Fluid Flow (Minneapolis: University of Minnesota) pp20−30
[27] 胡彪, 宁利中, 宁碧波, 田伟利, 吴昊, 宁景昊 2017 水动力学研究与进展 32 336
Google Scholar
Hu B, Ning L Z, Ning B B, Tian W L, Wu H, Ning J H 2017 Chin. J. Hydrodyn. 32 336
Google Scholar
下载:
计量
- 文章访问数: 6024
- PDF下载量: 68
- 被引次数: 0
