部分相干衍射成像综述

许文慧; 宁守琮; 张福才

doi:10.7498/aps.70.20211020

摘要

相干衍射成像是一种对光源相干性要求非常高的无透镜计算成像技术. 相干性包括时间相干性和空间相干性两方面, 在很多实际场合具有理想相干性的光源很难获得. 导致空间部分相干的因素主要有光源发光区域内各部分不同步的发光机制、检测器像素有限大小引起的非零宽度点扩散函数以及样品的不稳定性; 而时间部分相干则是由光源的能量扩散引起, 表现为扩展的发射光谱带宽. 空间和时间相干性退化的直接结果是衍射图样的清晰度和可见度的降低, 导致相干衍射成像中基于全相干模型构建的重构算法无法实现准确的物体波前重构. 解决方法包括改良实验装置来直接提高光束的相干性, 和通过优化相位恢复算法来补偿相干性退化的影响. 基于Wolf的相干模表示方法和Nugent等建立的部分相干衍射成像理论框架, 针对不同相干衍射成像技术中低相干性问题的各种解决办法相继被提出, 总体历经了从需要提前测出照明光的空间相干特征 (相干长度或者复相干因子) 或者时间相干特征(光谱分布) 到不需要任何已知光源相干特征的发展过程. 本文重点介绍相干衍射成像的部分相干性理论、以及部分空间和部分时间相干光衍射成像中重构算法的研究进展.

关键词:

Abstract

Coherent diffraction imaging (CDI), a type of lensless imaging method, relies on the use of light source with high-degree coherence to compute highly resolved complex-valued objects. The coherence of light source consists of temporal coherence and spatial coherence. In practice, it is difficult to obtain a fully coherent source. Spatial decoherence can be generated in the following three scenarios: no synchronization mechanism for the whole radiation source, a finite (non-zero) point spread function of the detector, and the sample variation within exposure time. Partial temporal coherence means that the beam is not quasi-monochromatic, behaving as the energy spread of the illumination. The consequence of reduced degree of temporal and/or spatial coherence in CDI is the decrease of visibility in the measured diffraction intensity. A fundamental assumption of CDI is the full temporal and spatial coherence, and even a relatively small deviation from full coherence can prevent the phase retrieval algorithm from converging accurately. It is necessary to break the barrier of limited coherence by improving the experimental setups directly or optimizing the phase retrieval algorithms to mitigate decoherence. Based on the Wolf’s model of coherence-mode of light and the framework of CDI using partially coherent light proposed by Nugent et al., various methods have been proposed to solve the problems induced by low coherence. Those methods generally experience a similar development process, that is, from the requirement for measuring the spatial (coherent length or complex coherent factor) or temporal (spectrum distribution) coherence properties to without the need for such priori knowledge. Here in this work, the principles of partial coherent CDI, and the major progress of CDI with partial spatial- and temporal-coherent light are reviewed.

Keywords:

作者及机构信息

1.
哈尔滨工业大学, 哈尔滨　150001

2.
南方科技大学电子与电气工程系, 深圳　518055

3.
新加坡国立大学材料科学与工程系, 新加坡　117575

通信作者: 张福才, zhangfc@sustech.edu.cn

基金项目: 国家自然科学基金(批准号: 11775105, 12074167)、深圳市孔雀计划团队项目(批准号: KQTD20170810110313773)和南方科技大学-麻省理工机械工程教育科研中心项目(批准号: 6941806)资助的课题.

Authors and contacts

1.
Harbin Institute of Technology, Harbin 150001, China

2.
Department of Electrical and Electronic Engineering, Southern University of Science and Technology, Shenzhen 518055, China

3.
Department of Materials Science and Engineering, National University of Singapore, Singapore 117575, Singapore

Corresponding author: Zhang Fu-Cai, zhangfc@sustech.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11775105, 12074167), the Shenzhen Science and Technology Program, China (Grant No. KQTD20170810110313773), and the Centers for Mechanical Engineering Research and Education at MIT and SUSTech (MechERE Centers at MIT and SUSTech) (Grant No. 6941806).

文章全文 : translate this paragraph

参考文献

[1]	Nelson J, Huang X, Steinbrener J, Shapiro D, Kirz J, Marchesini S, Neiman A M, Turner J J, Jacobsen C 2010 Proc. Natl Acad. Sci. USA 107 7235 Google Scholar
[2]	Shapiro D A, Yu Y S, Tyliszczak T, Cabana J, Celestre R, Chao W, Kaznatcheev K, Kilcoyne A L D, Maia F, Marchesini S, Meng Y S, Warwick T, Yang L L, Padmore H A 2014 Nat. Photonics 8 765 Google Scholar
[3]	Holler M, Guizar-Sicairos M, Tsai E H R, Dinapoli R, Müller E, Bunk O, Raabe J, Aeppli G 2017 Nature 543 402 Google Scholar
[4]	Holler M, Odstrčil M, Guizar-Sicairos M, Lebugle M, Müller E, Finizio S, Tinti G, David C, Zusman J, Unglaub W, Bunk O, Raabe J, Levi A F J, Aeppli G 2019 Nat. Electron. 2 464 Google Scholar
[5]	Seaberg M D, Zhang B, Gardner D F, Shanblatt E R, Murnane M M, Kapteyn H C, Adams D E 2014 Optica 1 39 Google Scholar
[6]	Sayre D 1952 Acta Cryst. 5 843 Google Scholar
[7]	Sayre D 1980 Imaging Processes and Coherence in Physics (Vol. 112) (Berlin, Heidelberg: Springer) pp229−235
[8]	Fratz M, Seyler T, Bertz A, Carl D 2021 Light-Adv. Manu. 2 15 Google Scholar
[9]	Bianco V, Memmolo P, Leo M, Montresor S, Distante C, Paturzo M, Picart P, Javidi B, Ferraro P 2018 Light-Adv. Manu. 7 347 Google Scholar
[10]	Nelson J W, Knefelkamp G R, Brolo A G, Lindquist N C 2018 Light-Adv. Manu. 7 496 Google Scholar
[11]	Miao J, Charalambous P, Kirz J, Sayre D 1999 Nature 400 342 Google Scholar
[12]	Williams G J, Quiney H M, Dhal B B, Tran C Q, Nugent K A, Peele A G, Paterson D, Jonge M D de 2006 Phys. Rev. Lett. 97 025506 Google Scholar
[13]	Abbey B, Nugent K A, Williams G J, Clark J N, Peele A G, Pfeifer M A, De Jonge M, McNulty I 2008 Nat. Phys. 4 394 Google Scholar
[14]	Hoppe W 1969 Acta Crystallogr. 25 495 Google Scholar
[15]	Rodenburg J M, Hurst A C, Cullis A G, Dobson B R, Pfeiffer F, Bunk O, David C, Jefimovs K, Johnson I 2007 Phys. Rev. Lett. 98 034801 Google Scholar
[16]	Guizar-Sicairos M, Fienup J R 2008 Opt. Express 16 7264 Google Scholar
[17]	Zheng G, Horstmeyer R, Yang C 2013 Nat. Photonics 7 739 Google Scholar
[18]	Zheng G 2014 IEEE Photon. J. 6 1 Google Scholar
[19]	Zhang F, Pedrini G, Osten W 2007 Phys. Rev. A 75 043805 Google Scholar
[20]	Zhang F, Rodenburg J M 2010 Phys. Rev. B 82 121104 Google Scholar
[21]	Zhang F, Chen B, Morrison G R, Vila-Comamala Joan, Guizar-Sicairos M, Robinson I K 2016 Nat. Commun. 7 13367 Google Scholar
[22]	He Z, Wang B, Bai J, Barbastathis G, Zhang F 2020 Ultramicroscopy 214 112990 Google Scholar
[23]	Wang B, Wang Q, Lyu W, Zhang F 2020 Ultramicroscopy 216 113034 Google Scholar
[24]	Roy S, Parks D, Seu K A, Su R, Turner J J, Chao W, Anderson E H, Cabrini S, Kevan S D 2011 Nat. Photonics 5 243 Google Scholar
[25]	Gardner D F, Zhang B, Seaberg M D, Martin L S, Adams D E, Salmassi F, Gullikson E, Kapteyn H, Murnane M 2012 Opt. Express 20 19050 Google Scholar
[26]	Robinson I K, Vartanyants I A, Williams G J, Pfeifer M A, Pitney J A 2001 Phys. Rev. Lett. 87 195505 Google Scholar
[27]	Pfeifer M A, Williams G J, Vartanyants I A, Harder R, Robinson I K 2006 Nature 442 63 Google Scholar
[28]	Dierolf M, Menzel A, Thibault P, Schneider P, Kewish C M, Wepf R, Bunk O, Pfeiffer F 2010 Nature 467 436 Google Scholar
[29]	Barty A, Sébastien B, Bogan M J, Hau-Riege S, Marchesini S, Sokolowski-Tinten K, Stojanovic N, Tobey R, Ehrke H, Cavalleri A, Düsterer S, Frank M, Bajt S, Woods B W, Seibert M M, Hajdu J, Treusch R, Chapman H N 2008 Nat. Photonics 2 415 Google Scholar
[30]	Rodenburg J M, Bates R H T 1992 Philosophical Transactions of the Royal Society of London. Series A: Physical and Engineering Sciences 339 521 Google Scholar
[31]	Gureyev T E, Nugent K A 1997 Opt. Commun. 133 339 Google Scholar
[32]	Gerchberg R W, Saxton W O 1971 Optik (Stuttgart) 34 275
[33]	Gerchberg R W, Saxton W O 1972 Optik 35 237
[34]	Fienup J R 1978 Opt. Lett. 3 27 Google Scholar
[35]	Fienup J R 1982 Appl. Opt. 21 2758 Google Scholar
[36]	杨国桢, 顾本源 1981 30 410 Google Scholar Yang G, Gu B 1981 Acta Phys. Sin. 30 410 Google Scholar
[37]	Luke D R 2005 Inverse Prob. 21 37 Google Scholar
[38]	Faulkner H M L, Rodenburg J M 2004 Phys. Rev. Lett. 93 023903 Google Scholar
[39]	Thibault P, Dierolf M, Bunk O, Menzel A, Pfeiffer F 2009 Ultramicroscopy 109 338 Google Scholar
[40]	Maiden A M, Rodenburg J M 2009 Ultramicroscopy 109 1256 Google Scholar
[41]	Barbastathis G, Ozcan A, Situ G 2019 Optica 6 921 Google Scholar
[42]	Li S, Deng M, Lee J, Sinha A, and Barbastathis G 2018 Optica 5 803 Google Scholar
[43]	Rivenson Y, Zhang Y, Gunaydin H, Da T, Ozcan A 2018 Light-Sci. Appl. 7 17141 Google Scholar
[44]	Wang F, Bian Y, Wang H, Lyu Meng, Pedrini G, Osten W, Barbastathis G, Situ G 2020 Light-Sci. Appl. 9 1 Google Scholar
[45]	Simon R, Sudarshan E C G, Mukunda N 1984 Phys. Rev. A 29 3273 Google Scholar
[46]	Friberg A T, Sudol R J 1982 Opt. Commun. 41 383 Google Scholar
[47]	Starikov A, Wolf E Wolf E 1982 J. Opt. Soc. Am. 72 923 Google Scholar
[48]	Bagini V, Frezza F, Santarsiero M, Schettini G, Spagnolo G S 1996 J. Mod. Opt. 43 1155 Google Scholar
[49]	Ponomarenko S A 2001 J. Opt. Soc. Am. A 18 150 Google Scholar
[50]	Gori F, Guattari G, Padovani C 1987 Opt. Commun. 64 311 Google Scholar
[51]	Gbur G, Visser T D 2010 Progress in Optics 55 285 Google Scholar
[52]	Wolf E 1982 J. Opt. Soc. Am. 72 343 Google Scholar
[53]	Smithies F 1970 Integral Equations (Cambridge: Cambridge U. Press) p128
[54]	Quiney H M 2010 J. Mod. Optic. 57 1109 Google Scholar
[55]	Nugent K A 2010 Adv. Phys. 59 1 Google Scholar
[56]	Sinha S K, Tolan M, Gibaud A 1998 Phys. Rev. B 57 2740 Google Scholar
[57]	Lin B, Schlossman M L, Meron M, Williams S M, Huang Z, Viccaro P J 1998 Phys. Rev. B 58 8025 Google Scholar
[58]	Vartanyants I A, Robinson I K 2001 J. Phys. Condens. Matter 13 10593 Google Scholar
[59]	Spence J C H, Weierstall U, Howells M 2004 Ultramicroscopy 101 149 Google Scholar
[60]	Nugent K A 1991 J. Opt. Soc. Am. A 8 1574 Google Scholar
[61]	Williams G J, Quiney H M, Peele A G, Nugent K A 2007 Phys. Rev. B 75 104102 Google Scholar
[62]	Lin J J A, Paterson D, Peele A G, McMahon P J, Chantler C T, Nugent K A, Lai B, Moldovan N, Cai Z, Mancini D C, McNulty I 2003 Phys. Rev. Lett. 90 074801 Google Scholar
[63]	Whitehead L W, Williams G J, Quiney H M, Dilanian R A, Flewett S, Nugent K A, Peele A G, Balaur E, McNulty I 2009 Phys. Rev. Lett. 103 243902 Google Scholar
[64]	Abbey B, Whitehead L W, Quiney H M, Vine D, Cadenazzi G A, Henderson C A, Nugent K A, Balaur E, Putkunz C T, Peele A G, Williams G J, McNulty I 2011 Nat. Photonics 5 420 Google Scholar
[65]	Whitehead L W, Williams G J, Quiney H M, Nugent K A, Peele A G, Paterson D, Jonge M D de, McNulty I 2008 Phys. Rev. B 77 104112 Google Scholar
[66]	Flewett S, Quiney H M, Tran C Q, Nugent K A 2009 Opt. Lett. 34 2198 Google Scholar
[67]	Paterson D, Allman B E, Mcmahon P J, Lin J, Moldovan N, Nugent K A, McNulty I, Chantler C T, Retsch C C, Irving T H K, Mancini D C 2001 Opt. Commun. 195 79 Google Scholar
[68]	Partanen H, Turunen J, Tervo J 2014 Opt. Lett. 39 1034 Google Scholar
[69]	Pfeiffer F, Bunk O, Schulzebriese C, Diaz A, Weitkamp T, David C, Veen J F van der, Vartanyants I, Robinson I K 2005 Phys. Rev. Lett. 94 164801 Google Scholar
[70]	Morrill D, Li D, Pacifici D 2016 Nat. Photonics 10 681 Google Scholar
[71]	Marathe S, Shi X, Wojcik M J, Kujala N G, Divan R, Mancini D C, Macrander A T, Assoufid L 2014 Opt. Express 22 14041 Google Scholar
[72]	Shi X, Marathe S, Wojcik M, Kujala N G, Macrander A T, Assoufid L 2014 Appl. Phys. Lett. 105 41116 Google Scholar
[73]	Tran C Q, Peele A G, Roberts A, Nugent K A 2005 Opt. Lett. 30 204 Google Scholar
[74]	Tran C Q, Williams G J, Roberts A, Flewett S, Peele A G, Paterson D, Jonge M D de, Nugent K A 2007 Phys. Rev. Lett. 98 224801 Google Scholar
[75]	Shao Y, Lu X, Konijnenberg S, Zhao C, Cai Y, Urbach H P 2018 Opt. Express 26 4479 Google Scholar
[76]	Clark J N, Peele A G 2011 Appl. Phys. Lett. 99 154103 Google Scholar
[77]	Clark J N, Huang X, Harder R, Robinson I K 2012 Nat. Commun. 3 993 Google Scholar
[78]	Tran G N, Van Riessen G A, Peele A G 2017 Opt. Express 25 10757 Google Scholar
[79]	Parks D H, Shi X, Kevan S D 2014 Phys. Rev. A 89 063824 Google Scholar
[80]	Hagemann J, Salditt T 2018 Opt. Express 26 242 Google Scholar
[81]	Burdet N, Shi X, Parks D, Clark J N, Huang X, Kevan S D, Robinson I K 2015 Opt. Express 23 5452 Google Scholar
[82]	Cadenazzi G, Chen B, Gureyev T, Quiney H M, Nugent K A, Abbey B 2018 Proceedings of the Nanophotonics Australasia 2017 Melbourne, Australia, December 11–13, 2017 p104565X
[83]	Thibault P, Menzel A 2013 Nature 494 68 Google Scholar
[84]	Cowley J M 1969 Appl. Phys. Lett. 15 58 Google Scholar
[85]	Martin A V, Quiney H M 2016 J. Phys. B 49 244001 Google Scholar
[86]	Clark J N, Huang X, Harder R J, Robinson I K 2014 Opt. Lett. 39 6066 Google Scholar
[87]	Huang X, Lauer K, Clark J N, Xu W 2015 Sci. Rep. 5 9074 Google Scholar
[88]	Pelz P M, Guizarsicairos M, Thibault P, Johnson I 2014 Appl. Phys. Lett. 105 251101 Google Scholar
[89]	Odstrcil M, Holler M, Guizar-sicairos M 2018 Opt. Express 26 12585 Google Scholar
[90]	Clark J N, Huang X, Harder R, Robinson I K 2014 Phys. Rev. Lett. 112 113901 Google Scholar
[91]	Stockmar M, Zanette I, Dierolf M, Enders B, Clare R, Pfeiffer F, Cloetens P, Bonnin A, Thibault P 2015 Phys. Rev. Appl. 3 014005 Google Scholar
[92]	Stockmar M, Hubert M, Dierolf M, Enders B, Clare R, Allner S, Fehringer A, Zanette I, Villanova J, Laurencin J, Cloetens P, Pfeiffer F, Thibault P 2015 Opt. Express 23 12720 Google Scholar
[93]	Helfenstein P, Rajeev R, Mochi I, Kleibert A, Vaz C A F, Ekinci Y 2018 Opt. Express 26 12242 Google Scholar
[94]	Cao S, Kok P, Li P, Maiden AM, Rodenburg J M 2016 Phys. Rev. A 94 63621 Google Scholar
[95]	Chen Z, Odstrcil M, Jiang Y, Han Y, Chiu M, Li L, Muller D A 2020 Nat. Commun. 11 2994 Google Scholar
[96]	Stachnik K, Mohacsi I, Vartiainen I, Stuebe N, Meyer J, Warmer M, David C, Meents A 2015 Appl. Phys. Lett. 107 11105 Google Scholar
[97]	Gardner D F, Divitt S, Watnik A T 2019 Appl. Opt. 58 3564 Google Scholar
[98]	Shen Q, Bazarov I, Thibault P 2004 J. Synchrotron Radiat. 11 432 Google Scholar
[99]	Wang Y, Yun W, Jacobsen C 2003 Nature 424 50 Google Scholar
[100]	Chen B, Dilanian R A, Teichmann S, Abbey B, Peele A G, Williams G J, Hannaford P, Dao L V, Quiney H M, Nugent K A 2009 Phys. Rev. A 79 23809 Google Scholar
[101]	Dilanian R A, Chen B, Williams G J, Quiney H M, Nugent K A, Teichmann S, Hannaford P, Dao L V, Peele A G 2009 J. Appl. Phys. 106 023110 Google Scholar
[102]	Dilanian R A, Chen B, Teichmann S, Dao L V, Quiney H M, Nugent K A 2008 Opt. Lett. 33 2341 Google Scholar
[103]	Walton A J 1986 Eur. J. Phys. 7 62 Google Scholar
[104]	Chapman H N, Barty A, Marchesini S, Noy A, Hau-Riege S P, Cui C, Howells M R, Rosen R A, He H, Spence J C H, Weierstall U, Beetz T, Jacobsen C, Shapiro D A 2006 J. Opt. Soc. Am. A 23 1179 Google Scholar
[105]	Huijts J, Fernandez S, Gauthier D, Kholodtsova M, Maghraoui A, Medjoubi K, Somogyi A, Boutu W, Merdji H 2020 Nat. Photonics 14 618 Google Scholar
[106]	Enders B, Dierolf M, Cloetens P, Stockmar M, Pfeiffer F, Thibault P 2014 Appl. Phys. Lett. 104 171104 Google Scholar
[107]	Odstrcil M, Baksh P, Kim H S, Boden S, Brocklesby W, Frey J 2015 X-ray Lasers and Coherent X-ray Sources: Development and Applications XI San Diego, United States, August 8–12, 2015 p958912
[108]	Pradier S R R, Riessen G van , Cadenazzi G A, Balaur E, Abbey B, Quiney H M 2016 XRM 2014: Proceedings of the 12th International Conference on X-Ray Microscopy Melbourne, Australia, October 26–31, 2016 p020048
[109]	Baksh P D, Odstrčil M, Kim H S, Boden S A, Frey J G, Brocklesby W S 2016 Opt. Lett. 41 1317 Google Scholar
[110]	Yao Y, Jiang Y, Klug J, Nashed Y, Roehrig C, Preissner C, Marin F, Wojcik M, Cossairt O, Cai Z, Vogt S, Lai B, Deng J 2021 J. Synchrotron Radiat. 28 309 Google Scholar
[111]	Parsons A D, Chapman R T, Baksh P, Mills B, Bajt S, Brocklesby W S, Frey J G 2013 J. Opt. 15 094009 Google Scholar
[112]	Marchesini S, He H, Chapman H N, Hau-Riege S P, Noy A, Howells M R, Weierstall U, Spence J 2003 Phys. Rev. B 68 140101 Google Scholar
[113]	Witte S, Tenner V T, Noom D W, Eikema K S 2014 Light-Sci. Appl. 3 e163 Google Scholar

施引文献

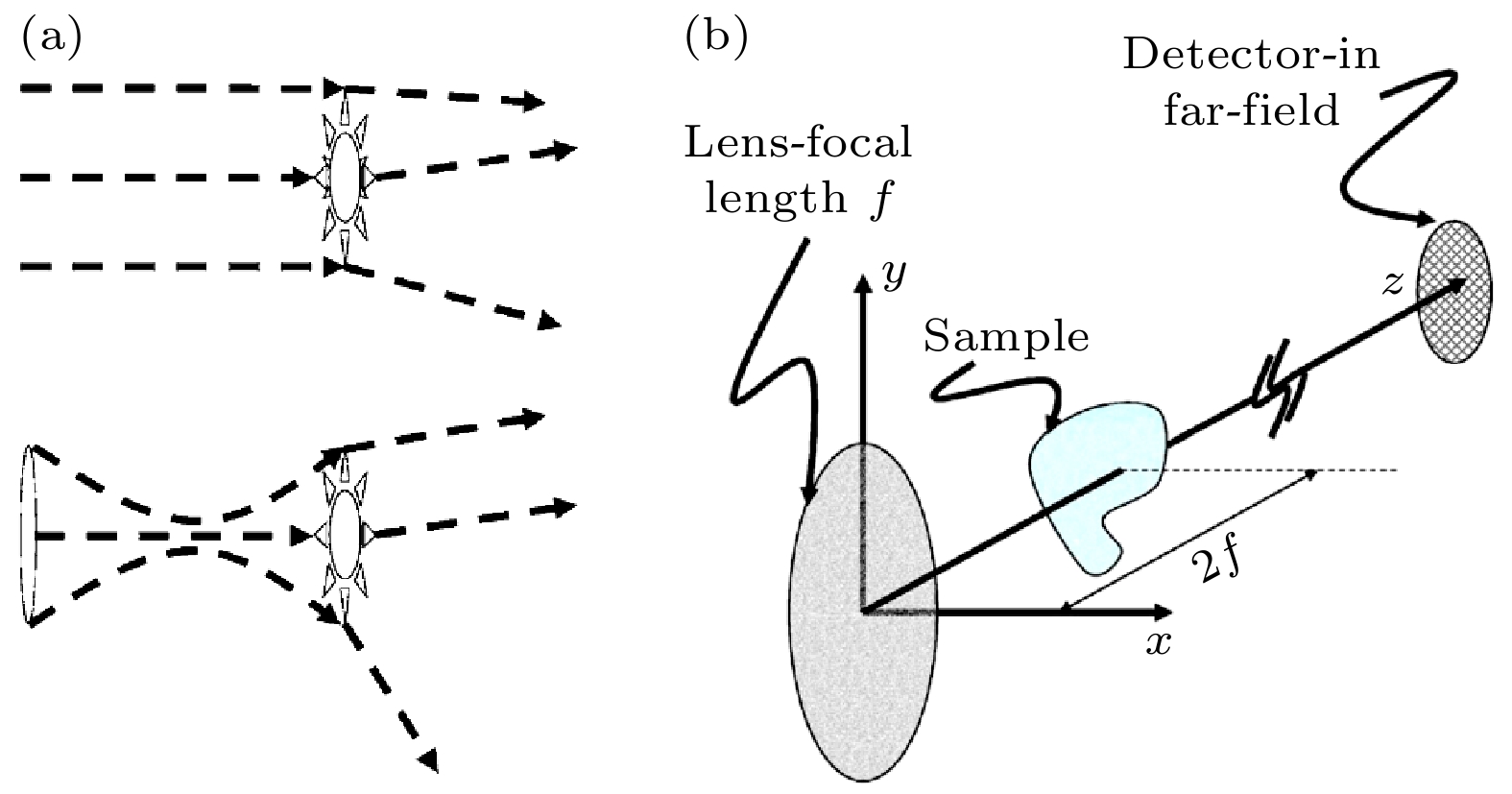
图 1 用于研究部分相干CDI的照明方式和成像系统^[61]　(a)平面波和球面波照明示意图, 透镜会引入额外的相位曲率, 假设透镜是理想的并且在物平面的相干长度是相同的; (b)实验系统模型示意图

Fig. 1. Schematics of the two illumination conditions and experimental system for investigating partially coherent CDI^[61]: (a) Illumination by planar and curved component waves, respectively. Assuming an ideal perfect lens, both have identical intensities and coherence lengths at the sample plane. However, the illumination with a lens has an additional phase curvature by the focal length of the lens; (b) the experimental system being modeled and the coordinate system used.

下载: 全尺寸图片幻灯片

图 2 低空间相干光照明时, 采用文献[63]多模算法(a)和单模算法(b)分别重构的物波强度信息; 在高空间相干光照明但已知相干长度信息不准确的情况下, 采用文献[63]多模算法(c)和单模算法(d)分别重构的物波强度信息^[63]

Fig. 2. Reconstruction of the magnitude of the wave leaving the sample. At the low-spatial coherent illumination, the reconstruction using the known coherence information (a) and assuming perfect spatial coherence (b). In the high-spatial coherent condition, reconstruction utilized the known coherence information (c) and full-spatial coherence assumption (d)^[63]

下载: 全尺寸图片幻灯片

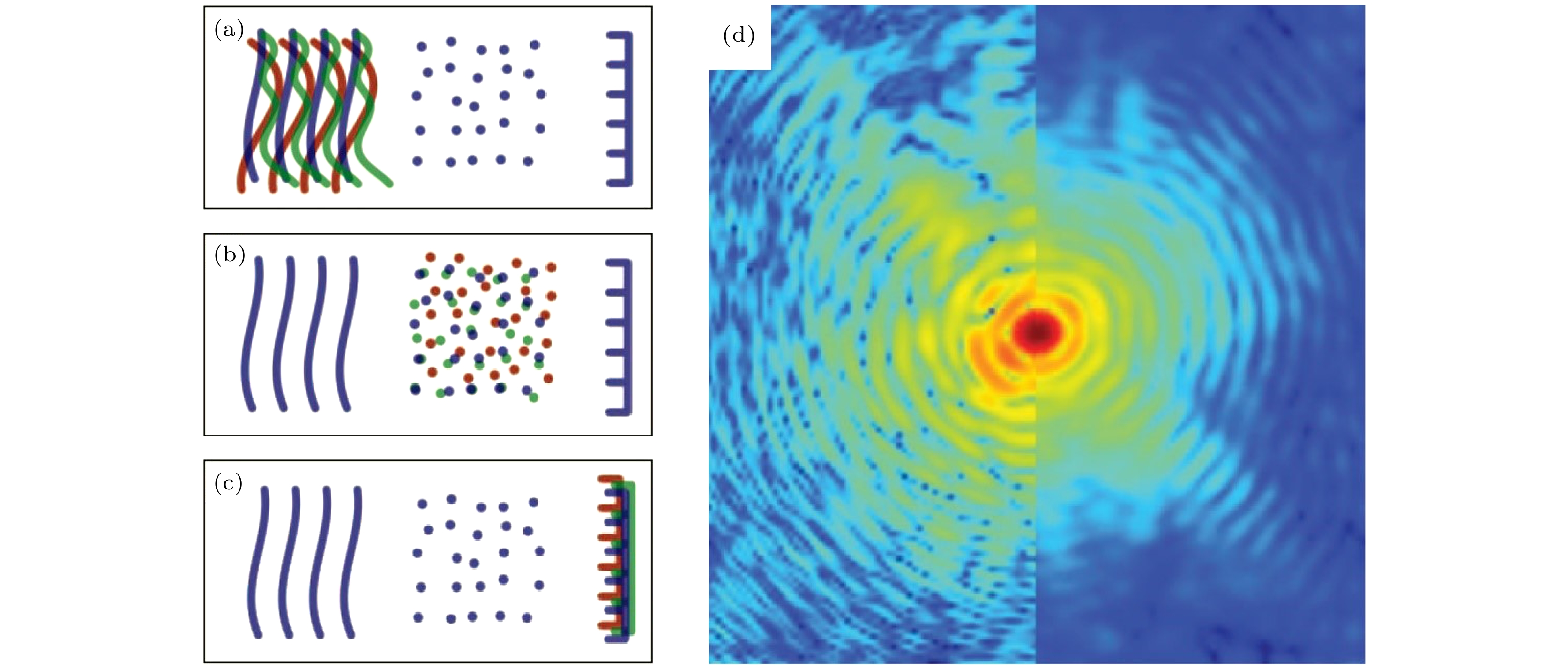
图 3 散射实验中的退相干现象^[83]　(a)由照明探针的横向相干性和有限的带宽引起的模态混合; (b)样品中的混合模态, 包括量子混合态和快速平稳随机过程, 如振动、开关或稳定流; (c)检测器的点扩散造成的模态混合; (d)对于远场衍射, 退相干会造成散射强度分布的可见度降低. 图(d)右半边是模拟样品振动给衍射图样带来的影响

Fig. 3. Decoherence in scattering experiments^[83]: (a) Mixed states within the probing radiation may include all sources of mixing that manifest themselves as transverse partial coherence or finite bandwidth; (b) mixed states in the object of interest may occur from quantum mixtures and fast stationary stochastic processes such as vibrations, switching or steady flows; (c) mixed states caused by the detector point spread; (d) the signature of decoherence in far-field diffraction is a decrease in visibility of the scattered intensity distribution. Here the right half of the simulated diffraction pattern shows the effect of sample vibration.

下载: 全尺寸图片幻灯片

图 4 伊辛模型成像模拟^[83]　(a) 在样本的布局中, 灰色方块代表每个自旋, 在照明光上产生±π/2的相移. 蓝色线条表示铁磁耦合, J = –1, 红色线条表示反铁磁耦合, J = +1; (b) 减去平均值后的4个主要物体模态. 相邻自旋正交化的结果, 在(b)中用蓝色和红色框勾勒出铁磁键(c)和反铁磁键(d), 相对模态的振幅与期望值非常吻合

Fig. 4. Imaging a simulated Ising model^[83]. (a) In the sample layout, grey squares mark individual spins, which incur a ±π/2 phase shift on the illumination. Blue lines represent ferromagnetic couplings, J = –1, red lines antiferromagnetic ones, J = +1. (b) The four dominant modes after subtraction of the mean. (c) and (d) The results of orthogonalization of neighbouring spins, outlined by blue and red frames in panel (b), for a ferromagnetic bond (c) and an antiferromagnetic bond (d). The relative mode amplitudes are in good agreement with expected values.

下载: 全尺寸图片幻灯片

图 5 (a)传统ptychography收集数据的模式, 即每移动距离r_j到1个位置静止后, 检测器才开始曝光进行数据的采集^[86]; (b) 样品以速度v进行连续运动时的数据采集模式, 每个r_j位置的衍射图样都是由在检测器曝光时间T内的$ \left| v \right|T $个位置的物波光子的叠加而得^[86]; (c) 样品以速度v进行连续运动时的数据采集模式可以被离散化, 即$ \left| v \right|T $可以离散化为n个小距离$ v\Delta t $^[86]; (d)—(f)样品相位的重构结果(左边1 mode是假设完全相干的情况, 右边5 modes是假设部分相干而将照明探针分解为5个模态的情况): (d)由原始采集数据直接重构的结果; (e)将相邻4个位置(总横跨距离是400 nm)采集的衍射图样叠加后重构的结果, 这里用相邻扫描位置对应衍射图的叠加来近似样品的连续运动^[86]; (f)将相邻7个位置(总横跨距离是700 nm)采集的衍射图样叠加后重构的结果^[86]

Fig. 5. (a) Conventional ptychography uses data collected with discrete translations r_j ^[86]; (b) for a continuously scanned sample with constant velocity v, the diffraction data will be made up of the positions that occupy a length $ \left| v \right|T $ around the scan positions r_j due to an integration time of T ^[86]; (c) the continuous scan can be discretized with steps separated by a small distance $ v\Delta t $^[86]; (d)−(f) reconstructed object phase (1 mode assuming full coherence, left and 5 modes assuming partial coherence, right): (d) Reconstruction for the original data^[86]; (e) reconstruction using new positions that consist of summing four adjacent positions (over 400 nm horizontally), approximating a continuously scanned sample^[86]; (f) reconstruction for a larger (seven positions, 700 nm) level of summing, which would be equivalent to an increased scanning speed^[86].

下载: 全尺寸图片幻灯片

图 6 (a)—(h)单层WS₂样品在不同电子剂量条件(58000和3300 e·Å^–2)下ptychography重构的结果; (i)—(p)单层WS₂样品在不同扫描步长(0.85和5.08 Å)下ptychography重构的结果; (a), (b)和(i), (j)分别分解为3个模态和2个模态重构的结果; (e), (f)和(m), (n)为不使用模态分解方法重构的结果; (c)和(d), (g)和(h), (k)和(l)以及(o)和(p)分别为对应于(a)和(b), (e)和(f), (i)和(j)以及(m)和(n)的衍射花样^[95]

Fig. 6. Ptychographic reconstructions of a monolayer WS₂ sample in different illumination dose (58000 and 3300 e·Å^–2, (a)−(h)) and different scan step size (0.85 and 5.08 Å, (i)−(p)) conditions^[95]: Mixed reconstructions from datasets using three ((a), (b)) and two ((i), (j)) probe modes, respectively; ((e), (f)) and ((m), (n)) single mode reconstructions; ((c), (d)), ((g), (h)), ((k), (l)) and ((o), (p)) corresponding diffractograms of ((a), (b)), ((e), (f)), ((i), (j)) and ((m), (n)).

下载: 全尺寸图片幻灯片

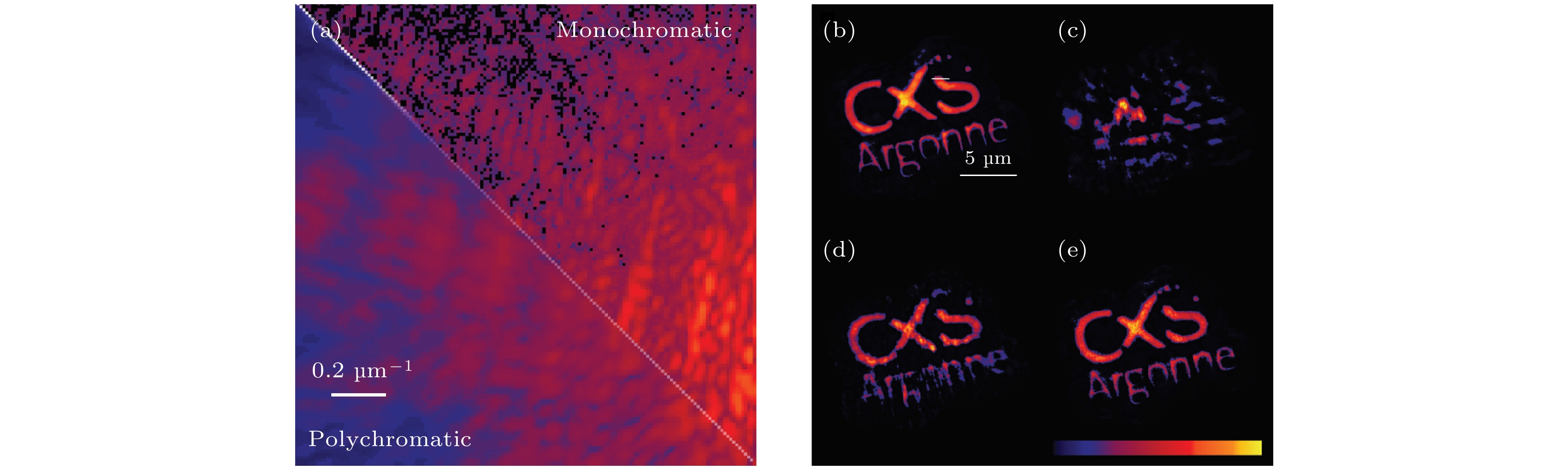
图 7 (a) 准单色光(右上)和宽带光(左下)照明所对应的部分衍射强度数据^[64]; (b)—(e) 重构的待测样品幅值信息(空间相干长度已知): (b) 准单色数据重构结果, 数据采集曝光时间为500 × 3 s, 重构时假设照明光完全相干^[64]; (c) 复色数据重构结果, 数据采集曝光时间为500 × 50 ms, 重构时假设照明光完全相干^[64]; (d) 复色数据重构结果, 重构时假设照明光完全相干, 但是采用从图(b)获得的物体精确尺寸作为初始支撑^[64]; (e) 复色数据重构结果, 采用和图(b)和(c)相同的重构过程, 但是重构算法为复色光衍射算法(polychromatic diffraction algorithm, PolyCDI)^[64]

Fig. 7. (a) Comparison of the quasi-monochromatic (upper right) and broadband (lower left) data^[64]. (b)−(e) Reconstructed amplitude of the sample (all reconstructions presented here use known spatial coherence information): (b) Reconstruction from quasi-chromatic data, collected with 500 × 5 s exposures, assuming full temporal coherence^[64]; (c) reconstruction from polychromatic data, collected with 500 × 50 ms exposures, assuming full temporal coherence^[64]; (d) reconstruction from polychromatic data assuming full temporal coherence but using the exact dimensions of the object (obtained from panel (b)) as the initial support^[64]; (e) reconstruction from polychromatic data using an identical procedure to panel (b) and (c) but using the polychromatic diffraction algorithm (PolyCDI)^[64].

下载: 全尺寸图片幻灯片

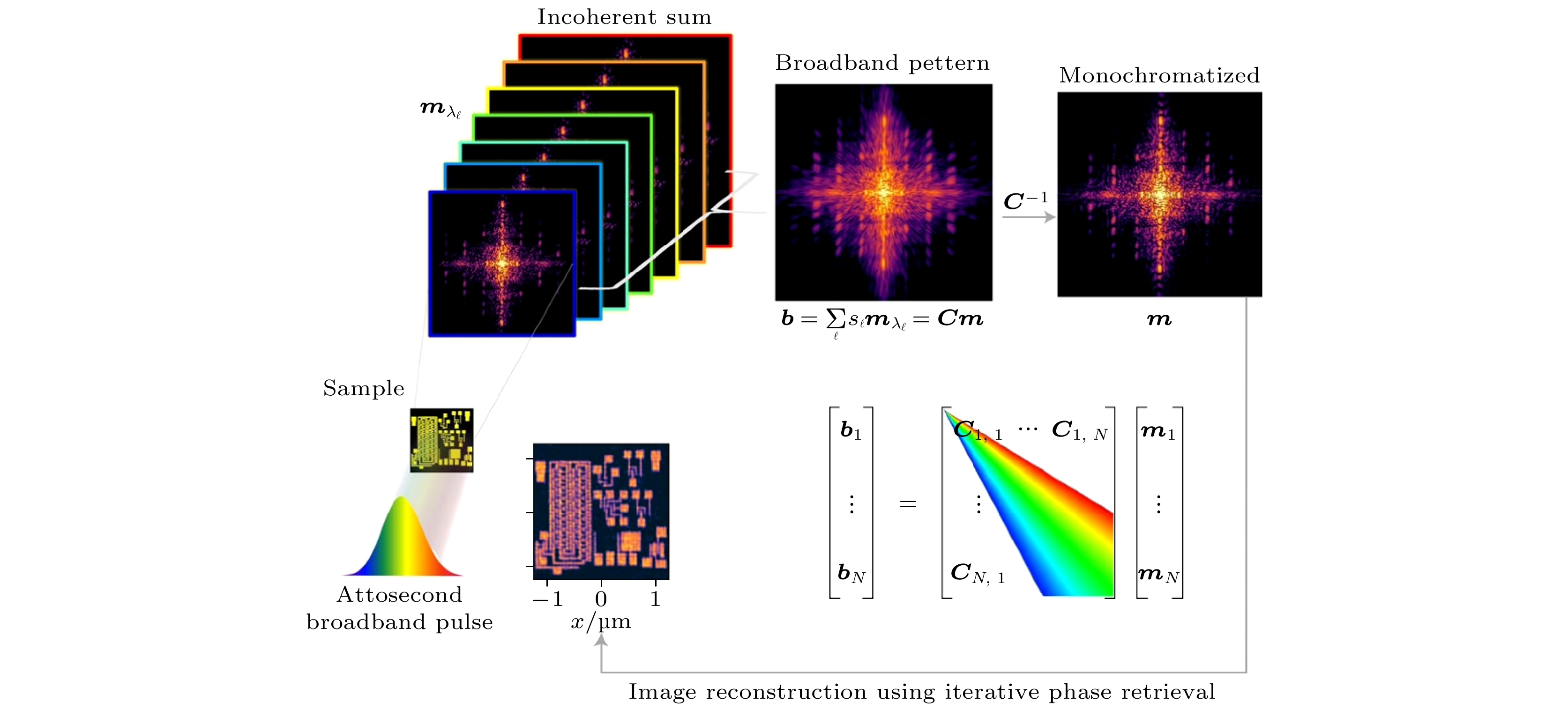
图 8 衍射图样数值单色化的原理图^[105]. 传统的CDI假设照明光源是单色的. 对于阿秒宽带光源, 衍射图样是所有波长所对应的单色衍射图样的加权叠加. 这些单色的衍射图样可以认为只有几何缩放的差别. 这种缩放是数值可逆的, 由矩阵C来表示该缩放矩阵. 确定了C之后, 就可以通过求解矩阵向量问题b = Cm从宽带光衍射图样b中提取出单色化的衍射图样m (图中右下部分所示为对应于一维衍射图样的简化情形). 然后就能直接将m代入到传统的相位恢复算法中重构出样品的复振幅信息. ℓ是复色光所包含的离散化光波的波长个数

Fig. 8. Principle of the numerical monochromatization^[105]. Conventional CDI assumes a monochromatic source. In the case of an attosecond broadband source, the diffraction pattern is the incoherent, spectrally weighted sum of the monochromatic diffraction patterns corresponding to all wavelengths presents in the sources. These monochromatic patterns are identical except for a geometric scaling. In the presented method this scaling is numerically inverted, and the scaling matrix is denoted by matrix C. The monochromatization method consists in the inversion of the matrix-vector problem b = Cm in order to retrieve the monochromatic diffraction pattern m from the broadband measurement b (The lower right part of the figure shows the simplified case for 1D diffraction pattern). Then m can be directly put into the conventional phase retrieval algorithm. ℓ is the index that corresponds to the spectral discretization.

下载: 全尺寸图片幻灯片

表 1 不同部分时间相干CDI方法的比较

Table 1. Comparison of different methods of partially temporal-coherent CDI.

方法	是否需要光谱信息	可适用的波的类型	最大带宽	实验结果
方法	是否需要光谱信息	可适用的波的类型	最大带宽	中心波长/nm	空间分辨率
Multiwavelength CDI^[100]	Yes	Discrete	Several harmonics	(35 ± 1)	(165 ± 5) nm
Two-step CDI^[101]	Yes	Discrete	Several harmonics	810	1 μm
PolyCDI^[64]	Yes	Continuous	11%	0.888	(150 ± 5) nm
Numerical monochromatization^[105]	Yes	Continuous	>10%	710	2.5 μm
Two-pulse imaging^[113]	No	Continuous	No limitation	47	6.7 μm

下载: 导出CSV

map

[1]	Nelson J, Huang X, Steinbrener J, Shapiro D, Kirz J, Marchesini S, Neiman A M, Turner J J, Jacobsen C 2010 Proc. Natl Acad. Sci. USA 107 7235 Google Scholar
[2]	Shapiro D A, Yu Y S, Tyliszczak T, Cabana J, Celestre R, Chao W, Kaznatcheev K, Kilcoyne A L D, Maia F, Marchesini S, Meng Y S, Warwick T, Yang L L, Padmore H A 2014 Nat. Photonics 8 765 Google Scholar
[3]	Holler M, Guizar-Sicairos M, Tsai E H R, Dinapoli R, Müller E, Bunk O, Raabe J, Aeppli G 2017 Nature 543 402 Google Scholar
[4]	Holler M, Odstrčil M, Guizar-Sicairos M, Lebugle M, Müller E, Finizio S, Tinti G, David C, Zusman J, Unglaub W, Bunk O, Raabe J, Levi A F J, Aeppli G 2019 Nat. Electron. 2 464 Google Scholar
[5]	Seaberg M D, Zhang B, Gardner D F, Shanblatt E R, Murnane M M, Kapteyn H C, Adams D E 2014 Optica 1 39 Google Scholar
[6]	Sayre D 1952 Acta Cryst. 5 843 Google Scholar
[7]	Sayre D 1980 Imaging Processes and Coherence in Physics (Vol. 112) (Berlin, Heidelberg: Springer) pp229−235
[8]	Fratz M, Seyler T, Bertz A, Carl D 2021 Light-Adv. Manu. 2 15 Google Scholar
[9]	Bianco V, Memmolo P, Leo M, Montresor S, Distante C, Paturzo M, Picart P, Javidi B, Ferraro P 2018 Light-Adv. Manu. 7 347 Google Scholar
[10]	Nelson J W, Knefelkamp G R, Brolo A G, Lindquist N C 2018 Light-Adv. Manu. 7 496 Google Scholar
[11]	Miao J, Charalambous P, Kirz J, Sayre D 1999 Nature 400 342 Google Scholar
[12]	Williams G J, Quiney H M, Dhal B B, Tran C Q, Nugent K A, Peele A G, Paterson D, Jonge M D de 2006 Phys. Rev. Lett. 97 025506 Google Scholar
[13]	Abbey B, Nugent K A, Williams G J, Clark J N, Peele A G, Pfeifer M A, De Jonge M, McNulty I 2008 Nat. Phys. 4 394 Google Scholar
[14]	Hoppe W 1969 Acta Crystallogr. 25 495 Google Scholar
[15]	Rodenburg J M, Hurst A C, Cullis A G, Dobson B R, Pfeiffer F, Bunk O, David C, Jefimovs K, Johnson I 2007 Phys. Rev. Lett. 98 034801 Google Scholar
[16]	Guizar-Sicairos M, Fienup J R 2008 Opt. Express 16 7264 Google Scholar
[17]	Zheng G, Horstmeyer R, Yang C 2013 Nat. Photonics 7 739 Google Scholar
[18]	Zheng G 2014 IEEE Photon. J. 6 1 Google Scholar
[19]	Zhang F, Pedrini G, Osten W 2007 Phys. Rev. A 75 043805 Google Scholar
[20]	Zhang F, Rodenburg J M 2010 Phys. Rev. B 82 121104 Google Scholar
[21]	Zhang F, Chen B, Morrison G R, Vila-Comamala Joan, Guizar-Sicairos M, Robinson I K 2016 Nat. Commun. 7 13367 Google Scholar
[22]	He Z, Wang B, Bai J, Barbastathis G, Zhang F 2020 Ultramicroscopy 214 112990 Google Scholar
[23]	Wang B, Wang Q, Lyu W, Zhang F 2020 Ultramicroscopy 216 113034 Google Scholar
[24]	Roy S, Parks D, Seu K A, Su R, Turner J J, Chao W, Anderson E H, Cabrini S, Kevan S D 2011 Nat. Photonics 5 243 Google Scholar
[25]	Gardner D F, Zhang B, Seaberg M D, Martin L S, Adams D E, Salmassi F, Gullikson E, Kapteyn H, Murnane M 2012 Opt. Express 20 19050 Google Scholar
[26]	Robinson I K, Vartanyants I A, Williams G J, Pfeifer M A, Pitney J A 2001 Phys. Rev. Lett. 87 195505 Google Scholar
[27]	Pfeifer M A, Williams G J, Vartanyants I A, Harder R, Robinson I K 2006 Nature 442 63 Google Scholar
[28]	Dierolf M, Menzel A, Thibault P, Schneider P, Kewish C M, Wepf R, Bunk O, Pfeiffer F 2010 Nature 467 436 Google Scholar
[29]	Barty A, Sébastien B, Bogan M J, Hau-Riege S, Marchesini S, Sokolowski-Tinten K, Stojanovic N, Tobey R, Ehrke H, Cavalleri A, Düsterer S, Frank M, Bajt S, Woods B W, Seibert M M, Hajdu J, Treusch R, Chapman H N 2008 Nat. Photonics 2 415 Google Scholar
[30]	Rodenburg J M, Bates R H T 1992 Philosophical Transactions of the Royal Society of London. Series A: Physical and Engineering Sciences 339 521 Google Scholar
[31]	Gureyev T E, Nugent K A 1997 Opt. Commun. 133 339 Google Scholar
[32]	Gerchberg R W, Saxton W O 1971 Optik (Stuttgart) 34 275
[33]	Gerchberg R W, Saxton W O 1972 Optik 35 237
[34]	Fienup J R 1978 Opt. Lett. 3 27 Google Scholar
[35]	Fienup J R 1982 Appl. Opt. 21 2758 Google Scholar
[36]	杨国桢, 顾本源 1981 30 410 Google Scholar Yang G, Gu B 1981 Acta Phys. Sin. 30 410 Google Scholar
[37]	Luke D R 2005 Inverse Prob. 21 37 Google Scholar
[38]	Faulkner H M L, Rodenburg J M 2004 Phys. Rev. Lett. 93 023903 Google Scholar
[39]	Thibault P, Dierolf M, Bunk O, Menzel A, Pfeiffer F 2009 Ultramicroscopy 109 338 Google Scholar
[40]	Maiden A M, Rodenburg J M 2009 Ultramicroscopy 109 1256 Google Scholar
[41]	Barbastathis G, Ozcan A, Situ G 2019 Optica 6 921 Google Scholar
[42]	Li S, Deng M, Lee J, Sinha A, and Barbastathis G 2018 Optica 5 803 Google Scholar
[43]	Rivenson Y, Zhang Y, Gunaydin H, Da T, Ozcan A 2018 Light-Sci. Appl. 7 17141 Google Scholar
[44]	Wang F, Bian Y, Wang H, Lyu Meng, Pedrini G, Osten W, Barbastathis G, Situ G 2020 Light-Sci. Appl. 9 1 Google Scholar
[45]	Simon R, Sudarshan E C G, Mukunda N 1984 Phys. Rev. A 29 3273 Google Scholar
[46]	Friberg A T, Sudol R J 1982 Opt. Commun. 41 383 Google Scholar
[47]	Starikov A, Wolf E Wolf E 1982 J. Opt. Soc. Am. 72 923 Google Scholar
[48]	Bagini V, Frezza F, Santarsiero M, Schettini G, Spagnolo G S 1996 J. Mod. Opt. 43 1155 Google Scholar
[49]	Ponomarenko S A 2001 J. Opt. Soc. Am. A 18 150 Google Scholar
[50]	Gori F, Guattari G, Padovani C 1987 Opt. Commun. 64 311 Google Scholar
[51]	Gbur G, Visser T D 2010 Progress in Optics 55 285 Google Scholar
[52]	Wolf E 1982 J. Opt. Soc. Am. 72 343 Google Scholar
[53]	Smithies F 1970 Integral Equations (Cambridge: Cambridge U. Press) p128
[54]	Quiney H M 2010 J. Mod. Optic. 57 1109 Google Scholar
[55]	Nugent K A 2010 Adv. Phys. 59 1 Google Scholar
[56]	Sinha S K, Tolan M, Gibaud A 1998 Phys. Rev. B 57 2740 Google Scholar
[57]	Lin B, Schlossman M L, Meron M, Williams S M, Huang Z, Viccaro P J 1998 Phys. Rev. B 58 8025 Google Scholar
[58]	Vartanyants I A, Robinson I K 2001 J. Phys. Condens. Matter 13 10593 Google Scholar
[59]	Spence J C H, Weierstall U, Howells M 2004 Ultramicroscopy 101 149 Google Scholar
[60]	Nugent K A 1991 J. Opt. Soc. Am. A 8 1574 Google Scholar
[61]	Williams G J, Quiney H M, Peele A G, Nugent K A 2007 Phys. Rev. B 75 104102 Google Scholar
[62]	Lin J J A, Paterson D, Peele A G, McMahon P J, Chantler C T, Nugent K A, Lai B, Moldovan N, Cai Z, Mancini D C, McNulty I 2003 Phys. Rev. Lett. 90 074801 Google Scholar
[63]	Whitehead L W, Williams G J, Quiney H M, Dilanian R A, Flewett S, Nugent K A, Peele A G, Balaur E, McNulty I 2009 Phys. Rev. Lett. 103 243902 Google Scholar
[64]	Abbey B, Whitehead L W, Quiney H M, Vine D, Cadenazzi G A, Henderson C A, Nugent K A, Balaur E, Putkunz C T, Peele A G, Williams G J, McNulty I 2011 Nat. Photonics 5 420 Google Scholar
[65]	Whitehead L W, Williams G J, Quiney H M, Nugent K A, Peele A G, Paterson D, Jonge M D de, McNulty I 2008 Phys. Rev. B 77 104112 Google Scholar
[66]	Flewett S, Quiney H M, Tran C Q, Nugent K A 2009 Opt. Lett. 34 2198 Google Scholar
[67]	Paterson D, Allman B E, Mcmahon P J, Lin J, Moldovan N, Nugent K A, McNulty I, Chantler C T, Retsch C C, Irving T H K, Mancini D C 2001 Opt. Commun. 195 79 Google Scholar
[68]	Partanen H, Turunen J, Tervo J 2014 Opt. Lett. 39 1034 Google Scholar
[69]	Pfeiffer F, Bunk O, Schulzebriese C, Diaz A, Weitkamp T, David C, Veen J F van der, Vartanyants I, Robinson I K 2005 Phys. Rev. Lett. 94 164801 Google Scholar
[70]	Morrill D, Li D, Pacifici D 2016 Nat. Photonics 10 681 Google Scholar
[71]	Marathe S, Shi X, Wojcik M J, Kujala N G, Divan R, Mancini D C, Macrander A T, Assoufid L 2014 Opt. Express 22 14041 Google Scholar
[72]	Shi X, Marathe S, Wojcik M, Kujala N G, Macrander A T, Assoufid L 2014 Appl. Phys. Lett. 105 41116 Google Scholar
[73]	Tran C Q, Peele A G, Roberts A, Nugent K A 2005 Opt. Lett. 30 204 Google Scholar
[74]	Tran C Q, Williams G J, Roberts A, Flewett S, Peele A G, Paterson D, Jonge M D de, Nugent K A 2007 Phys. Rev. Lett. 98 224801 Google Scholar
[75]	Shao Y, Lu X, Konijnenberg S, Zhao C, Cai Y, Urbach H P 2018 Opt. Express 26 4479 Google Scholar
[76]	Clark J N, Peele A G 2011 Appl. Phys. Lett. 99 154103 Google Scholar
[77]	Clark J N, Huang X, Harder R, Robinson I K 2012 Nat. Commun. 3 993 Google Scholar
[78]	Tran G N, Van Riessen G A, Peele A G 2017 Opt. Express 25 10757 Google Scholar
[79]	Parks D H, Shi X, Kevan S D 2014 Phys. Rev. A 89 063824 Google Scholar
[80]	Hagemann J, Salditt T 2018 Opt. Express 26 242 Google Scholar
[81]	Burdet N, Shi X, Parks D, Clark J N, Huang X, Kevan S D, Robinson I K 2015 Opt. Express 23 5452 Google Scholar
[82]	Cadenazzi G, Chen B, Gureyev T, Quiney H M, Nugent K A, Abbey B 2018 Proceedings of the Nanophotonics Australasia 2017 Melbourne, Australia, December 11–13, 2017 p104565X
[83]	Thibault P, Menzel A 2013 Nature 494 68 Google Scholar
[84]	Cowley J M 1969 Appl. Phys. Lett. 15 58 Google Scholar
[85]	Martin A V, Quiney H M 2016 J. Phys. B 49 244001 Google Scholar
[86]	Clark J N, Huang X, Harder R J, Robinson I K 2014 Opt. Lett. 39 6066 Google Scholar
[87]	Huang X, Lauer K, Clark J N, Xu W 2015 Sci. Rep. 5 9074 Google Scholar
[88]	Pelz P M, Guizarsicairos M, Thibault P, Johnson I 2014 Appl. Phys. Lett. 105 251101 Google Scholar
[89]	Odstrcil M, Holler M, Guizar-sicairos M 2018 Opt. Express 26 12585 Google Scholar
[90]	Clark J N, Huang X, Harder R, Robinson I K 2014 Phys. Rev. Lett. 112 113901 Google Scholar
[91]	Stockmar M, Zanette I, Dierolf M, Enders B, Clare R, Pfeiffer F, Cloetens P, Bonnin A, Thibault P 2015 Phys. Rev. Appl. 3 014005 Google Scholar
[92]	Stockmar M, Hubert M, Dierolf M, Enders B, Clare R, Allner S, Fehringer A, Zanette I, Villanova J, Laurencin J, Cloetens P, Pfeiffer F, Thibault P 2015 Opt. Express 23 12720 Google Scholar
[93]	Helfenstein P, Rajeev R, Mochi I, Kleibert A, Vaz C A F, Ekinci Y 2018 Opt. Express 26 12242 Google Scholar
[94]	Cao S, Kok P, Li P, Maiden AM, Rodenburg J M 2016 Phys. Rev. A 94 63621 Google Scholar
[95]	Chen Z, Odstrcil M, Jiang Y, Han Y, Chiu M, Li L, Muller D A 2020 Nat. Commun. 11 2994 Google Scholar
[96]	Stachnik K, Mohacsi I, Vartiainen I, Stuebe N, Meyer J, Warmer M, David C, Meents A 2015 Appl. Phys. Lett. 107 11105 Google Scholar
[97]	Gardner D F, Divitt S, Watnik A T 2019 Appl. Opt. 58 3564 Google Scholar
[98]	Shen Q, Bazarov I, Thibault P 2004 J. Synchrotron Radiat. 11 432 Google Scholar
[99]	Wang Y, Yun W, Jacobsen C 2003 Nature 424 50 Google Scholar
[100]	Chen B, Dilanian R A, Teichmann S, Abbey B, Peele A G, Williams G J, Hannaford P, Dao L V, Quiney H M, Nugent K A 2009 Phys. Rev. A 79 23809 Google Scholar
[101]	Dilanian R A, Chen B, Williams G J, Quiney H M, Nugent K A, Teichmann S, Hannaford P, Dao L V, Peele A G 2009 J. Appl. Phys. 106 023110 Google Scholar
[102]	Dilanian R A, Chen B, Teichmann S, Dao L V, Quiney H M, Nugent K A 2008 Opt. Lett. 33 2341 Google Scholar
[103]	Walton A J 1986 Eur. J. Phys. 7 62 Google Scholar
[104]	Chapman H N, Barty A, Marchesini S, Noy A, Hau-Riege S P, Cui C, Howells M R, Rosen R A, He H, Spence J C H, Weierstall U, Beetz T, Jacobsen C, Shapiro D A 2006 J. Opt. Soc. Am. A 23 1179 Google Scholar
[105]	Huijts J, Fernandez S, Gauthier D, Kholodtsova M, Maghraoui A, Medjoubi K, Somogyi A, Boutu W, Merdji H 2020 Nat. Photonics 14 618 Google Scholar
[106]	Enders B, Dierolf M, Cloetens P, Stockmar M, Pfeiffer F, Thibault P 2014 Appl. Phys. Lett. 104 171104 Google Scholar
[107]	Odstrcil M, Baksh P, Kim H S, Boden S, Brocklesby W, Frey J 2015 X-ray Lasers and Coherent X-ray Sources: Development and Applications XI San Diego, United States, August 8–12, 2015 p958912
[108]	Pradier S R R, Riessen G van , Cadenazzi G A, Balaur E, Abbey B, Quiney H M 2016 XRM 2014: Proceedings of the 12th International Conference on X-Ray Microscopy Melbourne, Australia, October 26–31, 2016 p020048
[109]	Baksh P D, Odstrčil M, Kim H S, Boden S A, Frey J G, Brocklesby W S 2016 Opt. Lett. 41 1317 Google Scholar
[110]	Yao Y, Jiang Y, Klug J, Nashed Y, Roehrig C, Preissner C, Marin F, Wojcik M, Cossairt O, Cai Z, Vogt S, Lai B, Deng J 2021 J. Synchrotron Radiat. 28 309 Google Scholar
[111]	Parsons A D, Chapman R T, Baksh P, Mills B, Bajt S, Brocklesby W S, Frey J G 2013 J. Opt. 15 094009 Google Scholar
[112]	Marchesini S, He H, Chapman H N, Hau-Riege S P, Noy A, Howells M R, Weierstall U, Spence J 2003 Phys. Rev. B 68 140101 Google Scholar
[113]	Witte S, Tenner V T, Noom D W, Eikema K S 2014 Light-Sci. Appl. 3 e163 Google Scholar

[1]	齐乃杰, 何小亮, 吴丽青, 刘诚, 朱健强. 探测器光电特性对叠层相干衍射成像的影响. , 2023, 72(15): 154202. doi: 10.7498/aps.72.20230603
[2]	李艳玲, 梅海平, 任益充, 张骏昕, 陶志炜, 艾则孜姑丽·阿不都克热木, 刘世韦. 湍流大气中随机粗糙表面激光回波空间相干性仿真. , 2022, 71(14): 140201. doi: 10.7498/aps.71.20212420
[3]	麻永俊, 李睿晅, 李逵, 张光银, 钮津, 麻云凤, 柯长军, 鲍捷, 陈英爽, 吕春, 李捷, 樊仲维, 张晓世. 基于高次谐波X射线光源的三维纳米相干衍射成像技术. , 2022, 71(16): 164205. doi: 10.7498/aps.71.20220976
[4]	葛银娟, 潘兴臣, 刘诚, 朱健强. 基于相干调制成像的光学检测技术. , 2020, 69(17): 174202. doi: 10.7498/aps.69.20200224
[5]	周光照, 胡哲, 杨树敏, 廖可梁, 周平, 刘科, 滑文强, 王玉柱, 边风刚, 王劼. 上海光源硬X射线相干衍射成像实验方法初探. , 2020, 69(3): 034102. doi: 10.7498/aps.69.20191586
[6]	李元杰, 何小亮, 孔艳, 王绶玙, 刘诚, 朱健强. 基于电子束剪切干涉的PIE成像技术研究. , 2017, 66(13): 134202. doi: 10.7498/aps.66.134202
[7]	陈顺意, 丁攀峰, 蒲继雄. 部分相干径向偏振光束传输中相干性研究. , 2015, 64(13): 134201. doi: 10.7498/aps.64.134201
[8]	余伟, 何小亮, 刘诚, 朱健强. 非相干照明条件下的ptychographic iterative engine成像技术. , 2015, 64(24): 244201. doi: 10.7498/aps.64.244201
[9]	何小亮, 刘诚, 王继成, 王跃科, 高淑梅, 朱健强. PIE成像中周期性重建误差的研究. , 2014, 63(3): 034208. doi: 10.7498/aps.63.034208
[10]	满天龙, 万玉红, 江竹青, 王大勇, 陶世荃. 孪生光束干涉法测量光源的空间相干性. , 2013, 62(21): 214203. doi: 10.7498/aps.62.214203
[11]	刘诚, 潘兴臣, 朱健强. 基于光栅分光法的相干衍射成像. , 2013, 62(18): 184204. doi: 10.7498/aps.62.184204
[12]	张东, 张磊, 史久林, 石锦卫, 弓文平, 刘大禾. 受激布里渊散射的线宽压缩及时间相干性. , 2012, 61(6): 064212. doi: 10.7498/aps.61.064212
[13]	王华, 闫帅, 闫芬, 蒋升, 毛成文, 梁东旭, 杨科, 李爱国, 余笑寒. 上海同步辐射装置波荡器光源空间相干性的研究. , 2012, 61(14): 144102. doi: 10.7498/aps.61.144102
[14]	江浩, 张新廷, 国承山. 基于菲涅耳衍射的无透镜相干衍射成像. , 2012, 61(24): 244203. doi: 10.7498/aps.61.244203
[15]	肖瑞, 侯静, 姜宗福. 激光器阵列的部分相干性对相干合成远场输出特性的影响. , 2008, 57(2): 853-859. doi: 10.7498/aps.57.853
[16]	王华, 王向朝, 曾爱军, 杨坤. 大气湍流对斜程传输准单色高斯-谢尔光束空间相干性的影响. , 2008, 57(1): 634-638. doi: 10.7498/aps.57.634
[17]	陈晓文, 汤明玥, 季小玲. 大气湍流对部分相干厄米-高斯光束空间相干性的影响. , 2008, 57(4): 2607-2613. doi: 10.7498/aps.57.2607
[18]	肖瑞, 周朴, 侯静, 姜宗福, 刘明. 激光器的部分相干性对光纤激光器阵列相干合成远场图样的影响. , 2007, 56(2): 819-823. doi: 10.7498/aps.56.819
[19]	倪光炯, 陈苏卿, 周谷声. 辐射的相干性和熵的增加. , 1982, 31(5): 585-603. doi: 10.7498/aps.31.585
[20]	王之江. 电磁辐射的相干性. , 1963, 19(5): 320-335. doi: 10.7498/aps.19.320

计量

文章访问数: 15339
PDF下载量: 994
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板