-
作为相干衍射成像技术的一种, 相干调制成像(coherent modulation imaging, CMI)是一种无透镜相位成像技术, 不同于多光斑相位恢复技术, 通过引入已知的强波前调制, CMI可以实现单次曝光下对入射波前的快速重建, 同时结构简单不需要参考光. 除了能够用于相位成像、解决脉冲光束的在线测量问题外, 本文将其用于精密光学元件(峰谷值(peak value, PV) ≤ 0.5λ, λ = 632.8 nm)的面型检测. 为验证其测量能力, 对10片口径80 mm、PV值介于0.1λ和0.5λ之间的石英窗口进行了重复测量, 相比于商业干涉仪的测量结果, CMI算法测量结果的峰谷比值的标准偏差是0.0305λ (λ = 632.8 nm), 均方根(root-mean-square, RMS)的标准偏差为0.0052λ, 对于PV和RMS的测量精度可达到0.1λ和0.01λ, 为研究其极限性能, 同时对PV = λ/20的平行平晶进行了对比测量, 分析了其噪声来源, 考虑到CMI测量算法仍有很大的改进空间, 其有望成为一种区别于干涉测量的新型高精度光学元件检测技术.As one of the coherent diffractive imaging (CDI) techniques, coherent modulation imaging (CMI) is a lensless phase imaging technology with diffraction limited resolution in theory. Unlike multiple measurement phase retrieval algorithms, the CMI can achieve fast convergence speed with single-shot measurement by introducing a pre-characterized random phase modulator. Besides, it has simple structure without reference wave based on iterative engine. Despite the fact that the matured phase imaging can be used to implement the on-line wave diagnostics of laser pulse, in this work we accurately measure the face-type of optical component with peak-to-valley value below 0.5λ (λ = 632.8 nm) by using the CMI for the first time. In order to verify its measurement capability, 10 quartz windows with a diameter of 80 mm and PV value between 0.1λ and 0.5λ are repeatedly measured. Compared with the results of commercial interferometer, the root mean square error (Root MSE) of the peak-to-valley (PV) ratio of the results of the CMI is 0.0305λ, and the Root MSE of the root mean square (RMS) is 0.00522λ. The measurement accuracy of PV ratio and RMS can reach 0.1λ and 0.01λ respectively. In addition, the parallel flat with PV ratio = λ/20 is measured and analyzed with CMI, and its noise level is also analyzed. Considering that the potential improvement of CMI is available in the future, the CMI is expected to become a new technique for optical metrology with high precision, which is different from interferometry.
-
Keywords:
- phase retrieval /
- iterative engine /
- optical metrology /
- coherent diffractive imaging
[1] Rodenburg J M 2008 Adv. Imaging Electron Phys. 150 87
Google Scholar
[2] Rodenburg J M, Hurst A C, Cullis A G, Dobson B R, Pfeiffer F, Bunk O, David C, Jefimovs K, Johnson I 2007 Phys. Rev. Lett. 98 034801
Google Scholar
[3] Shahmoradian S, Tsai E, Diaz A, Guizar-Sicairos M, Raabe J, Spycher L, Britschgi M, Ruf A, Stahlberg H, Holler M 2017 Sci. Rep. 7 1
Google Scholar
[4] Hoppe R, Reinhardt J, Hofmann G, Patommel J, Grunwaldt J D, Damsgaard C D, Wellenreuther G, Falkenberg G, Schroer C G 2013 Appl. Phys. Lett. 102 203104
Google Scholar
[5] Hüe F, Rodenburg J M, Maiden A M, Sweeney F, Midgley P A 2010 Phys. Rev. B. 82 121415
Google Scholar
[6] Shemilt L, Verbanis E, Schwenke J, Estandarte Ana K, Xiong G, Harder R, Parmar N, Yusuf M, Zhang F, Robinson Ian K 2015 Biophys. J. 108 706
Google Scholar
[7] Faulkner H M L, Rodenburg J M 2004 Phys. Rev. Lett. 93 023903
Google Scholar
[8] Pennycook T J, Martinez G T, Nellist P D, Meyer J C 2019 Ultramicroscopy. 196 131
Google Scholar
[9] Kahnt M, Becher J, Brückner D, Fam Y, Sheppard T, Weissenberger T, Wittwer F, Grunwaldt J D, Schwieger W, Schroer C G 2019 Optica 6 1282
Google Scholar
[10] Clark J N, Huang X, Harder R J, Robinson I K 2014 Opt. Lett. 39 6066
Google Scholar
[11] Odstrčil M, Holler M, Guizar-Sicairos M 2018 Opt. Express 26 12585
Google Scholar
[12] Zhang F, Rodenburg J M 2010 Phys. Rev. B 82 121104
Google Scholar
[13] Zhang F, Chen B, Morrison G R, Vila-Comamala J, Guizar-Sicairos M, Robinson I K 2016 Nat. Commun. 7 13367
Google Scholar
[14] Dong X, Pan X, Liu C, Zhu J 2019 High Power. Laser. Sci. 7 e48
Google Scholar
[15] Pan X, Veetil S, Liu C, Tao H, Jiang Y, Lin Q, Li X, Zhu J 2016 Laser Phys. Lett. 13 055001
Google Scholar
[16] Dong X, Pan X, Liu C, Zhu J 2018 Opt. Lett. 43 1762
Google Scholar
[17] He X, Tao H, Pan X, Liu C, Zhu J 2018 Opt. Express 26 6239
Google Scholar
[18] Haynam C, Wegner P, Auerbach J, Bowers M, Dixit S, Erbert G, Heestand G, Henesian M, Hermann M, Jancaitis K 2007 Appl. Opt. 46 3276
Google Scholar
[19] Tao H, Veetil S P, Cheng J, Pan X, Wang H, Liu C, Zhu J 2015 Appl. Opt. 54 1776
Google Scholar
[20] 柴立群, 于瀛洁, 石琦凯, 许乔, 温圣林, 侯晶 2010 中国激光 37 809
Google Scholar
Chai L Q, Yu Y J, Shi Q K, Xu Q, Wen S L, Hou J 2010 Chin. J. Las. 37 809
Google Scholar
-
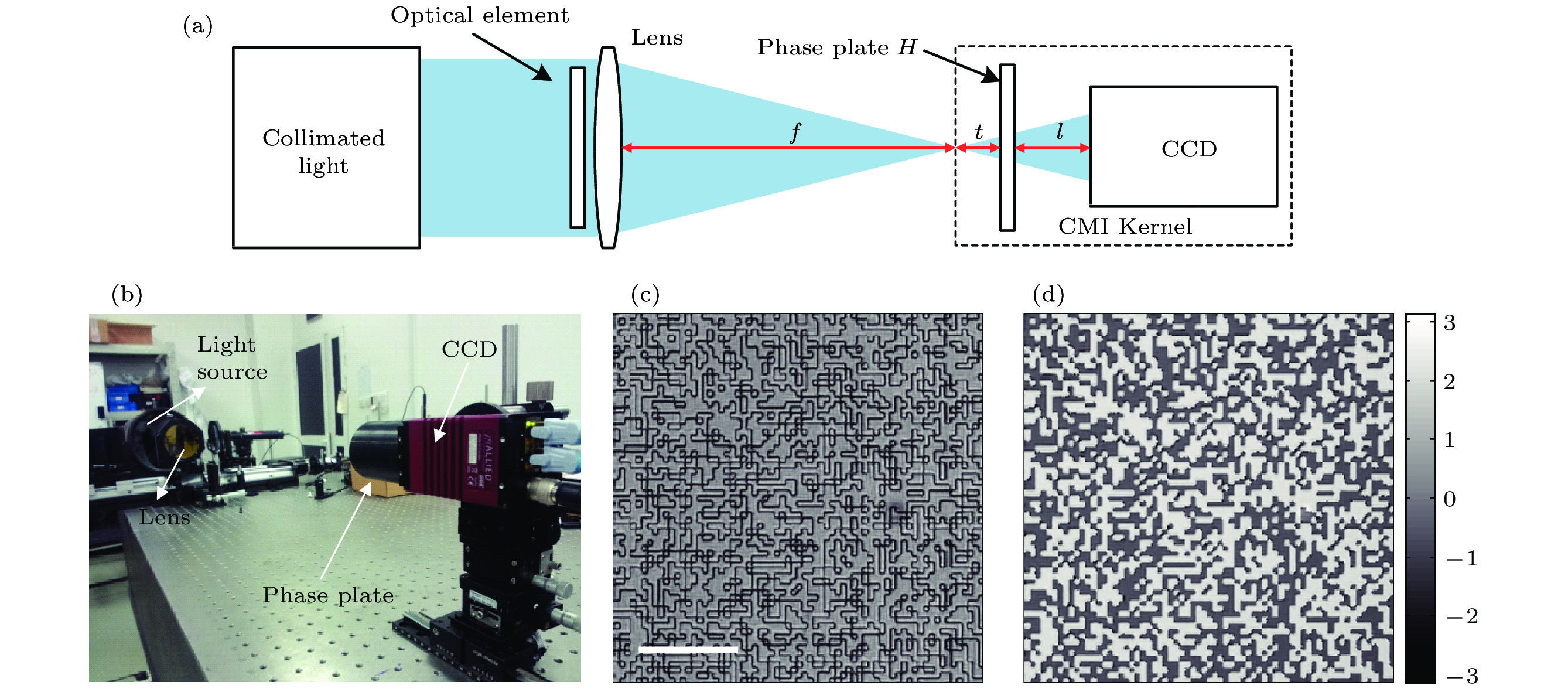
图 1 (a) CMI测量光学元件的基本光路; (b) 实验装置照片; (c), (d) 由ePIE算法标定的随机相位板振幅和相位分布, (c)中标尺长度为0.198 mm
Fig. 1. (a) Basic scheme for the measurement of optical components using CMI; (b) photo of the experimental setup; (c) amplitude and (d) phase of the center part of the random phase plate reconstructed by ePIE. The scale bar of (c) is 0.198 mm.
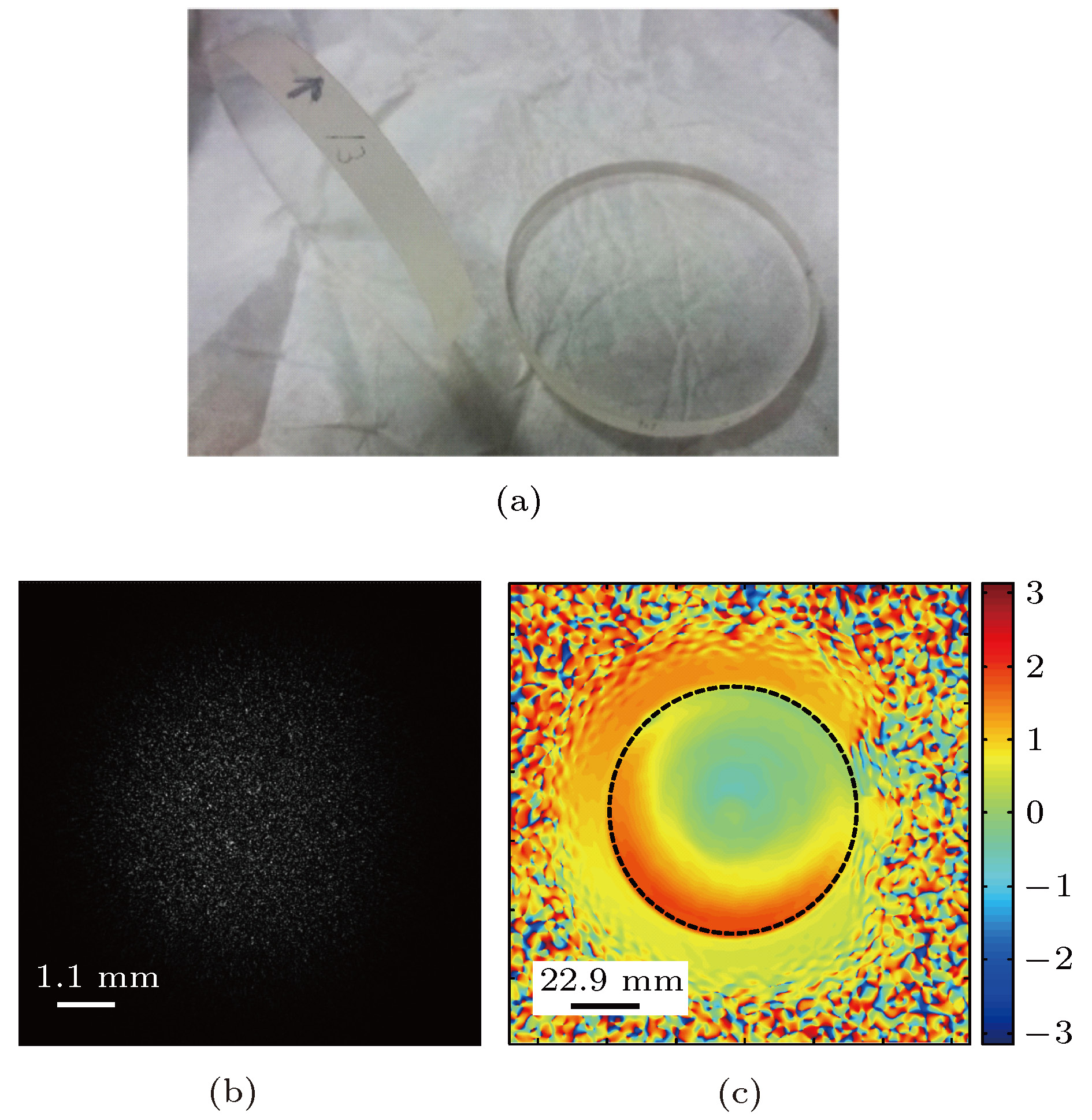
图 3 (a) 作为被测物的石英窗口; (b) CCD记录的衍射光斑; (c) 通过相位相减得到的石英窗口相位图, 其中由黑色虚线标记的区域的直径为79.1 mm
Fig. 3. (a) Photo of the plate glasses used in experiments; (b) diffraction pattern recorded by CCD; (c) phase map of plate glass obtained directly by phase subtraction. The section marked by the black dashed circle with a diameter of 79.1 mm is used for the analysis of PV and RMS. The constant phase slope is not removed for these calculations.
图 4 CMI和Zygo干涉仪的测量结果下, PV (a)和RMS (b)的最小二乘线性回归曲线
Fig. 4. Least-squares linear regressions of PV (a) and RMS (b) comparing the measurements from the CMI and Zygo interferometer.
图 5 分别由CMI和干涉仪测量的10个不同石英窗口的相位图
Fig. 5. Phase maps of ten different plate glasses measured by CMI and inteferometer.
图 6 (a) PV = λ/20的平行平晶照片; (b) 光学平面的相位图, 由Zygo干涉仪测得; (c)光学平面得相位图, 由CMI测得, λ = 632.8 nm
Fig. 6. (a) Photograph of an optical flat with PV = λ/20; phase maps of the optical flat, measured by the Zygo interferometer (b) and (c) by CMI. λ = 632.8 nm.
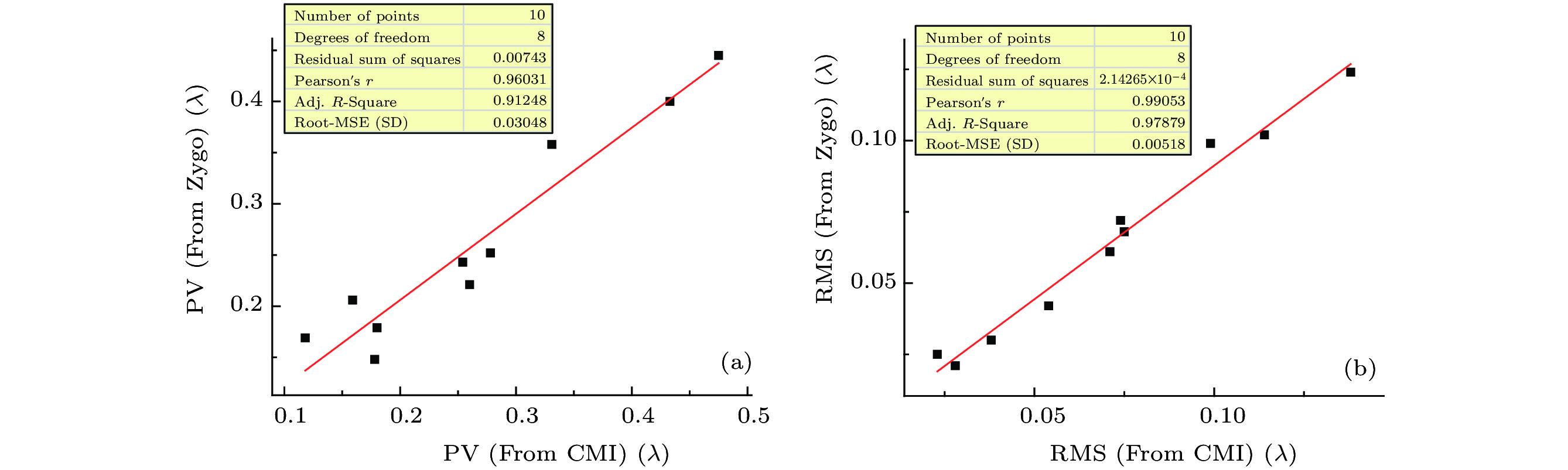
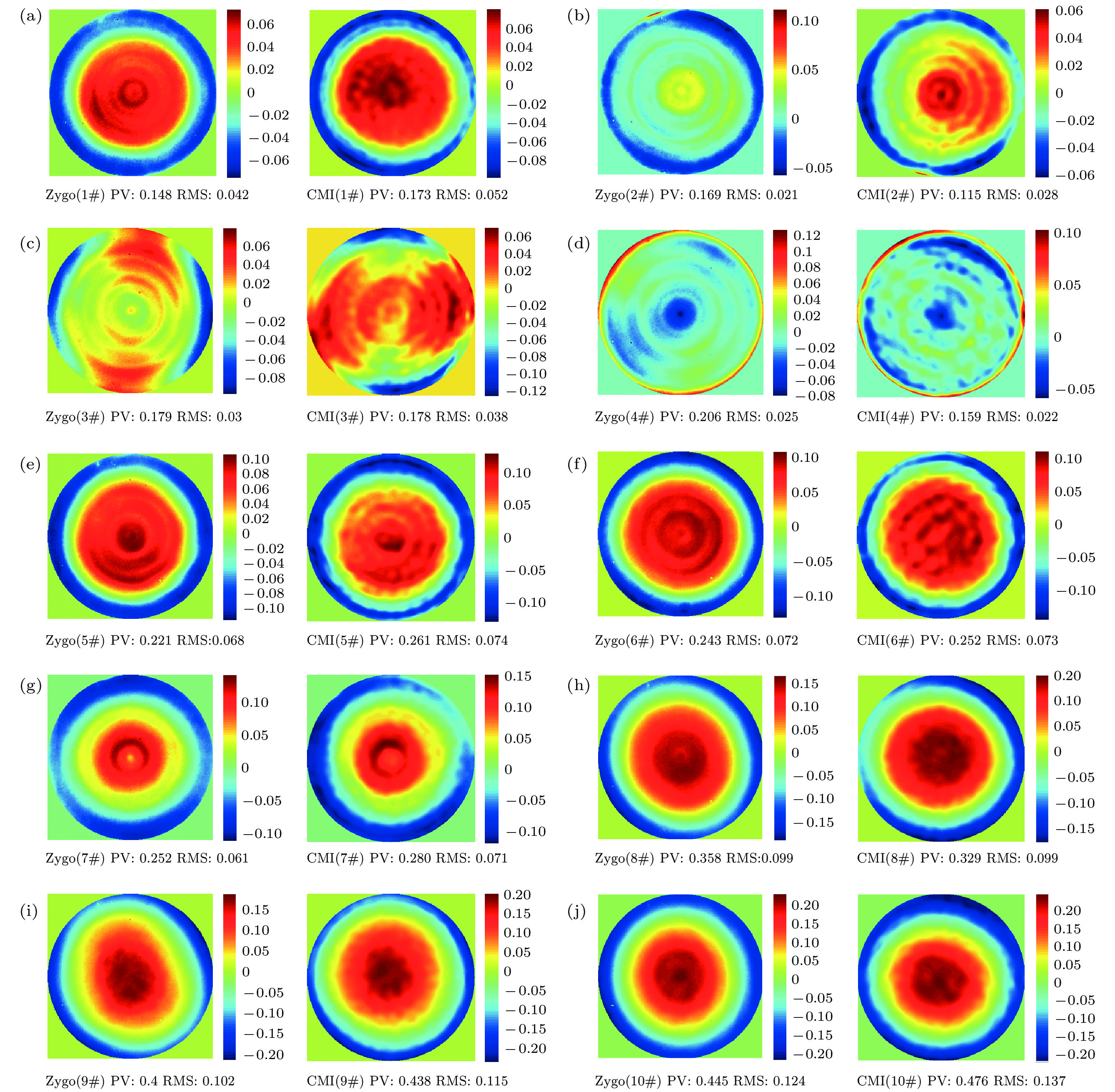
表 1 CMI和干涉仪的测量结果(λ)
Table 1. CMI and interferometer results (λ).
No. ${\overline {{\rm{PV}}} _{{\rm{CMI}}}}$ ${S_{{\rm{pv}}}}$ ${\rm{P}}{{\rm{V}}_{{\rm{Zygo}}}}$ ${\overline {{\rm{RMS}}} _{{\rm{CMI}}}}$ ${S_{{\rm{RMS}}}}$ ${\rm{RM}}{{\rm{S}}_{{\rm{Zygo}}}}$ 1 0.178 2.40 × 10–3 0.148 0.054 6.40 × 10–4 0.042 2 0.118 1.20 × 10–3 0.169 0.028 4.60 × 10–4 0.021 3 0.180 2.40 × 10–3 0.179 0.038 4.80 × 10–4 0.030 4 0.159 6.90 × 10–4 0.206 0.023 2.20 × 10–4 0.025 5 0.260 1.50 × 10–3 0.221 0.075 3.00 × 10–4 0.068 6 0.254 2.30 × 10–3 0.243 0.074 5.90 × 10–4 0.072 7 0.278 3.30 × 10–3 0.252 0.071 7.60 × 10–4 0.061 8 0.331 2.10 × 10–3 0.358 0.099 5.50 × 10–4 0.099 9 0.433 2.60 × 10–3 0.400 0.114 8.10 × 10–4 0.102 10 0.475 2.10 × 10–3 0.445 0.138 3.90 × 10–4 0.124 
下载: 导出CSV
-
[1] Rodenburg J M 2008 Adv. Imaging Electron Phys. 150 87
Google Scholar
[2] Rodenburg J M, Hurst A C, Cullis A G, Dobson B R, Pfeiffer F, Bunk O, David C, Jefimovs K, Johnson I 2007 Phys. Rev. Lett. 98 034801
Google Scholar
[3] Shahmoradian S, Tsai E, Diaz A, Guizar-Sicairos M, Raabe J, Spycher L, Britschgi M, Ruf A, Stahlberg H, Holler M 2017 Sci. Rep. 7 1
Google Scholar
[4] Hoppe R, Reinhardt J, Hofmann G, Patommel J, Grunwaldt J D, Damsgaard C D, Wellenreuther G, Falkenberg G, Schroer C G 2013 Appl. Phys. Lett. 102 203104
Google Scholar
[5] Hüe F, Rodenburg J M, Maiden A M, Sweeney F, Midgley P A 2010 Phys. Rev. B. 82 121415
Google Scholar
[6] Shemilt L, Verbanis E, Schwenke J, Estandarte Ana K, Xiong G, Harder R, Parmar N, Yusuf M, Zhang F, Robinson Ian K 2015 Biophys. J. 108 706
Google Scholar
[7] Faulkner H M L, Rodenburg J M 2004 Phys. Rev. Lett. 93 023903
Google Scholar
[8] Pennycook T J, Martinez G T, Nellist P D, Meyer J C 2019 Ultramicroscopy. 196 131
Google Scholar
[9] Kahnt M, Becher J, Brückner D, Fam Y, Sheppard T, Weissenberger T, Wittwer F, Grunwaldt J D, Schwieger W, Schroer C G 2019 Optica 6 1282
Google Scholar
[10] Clark J N, Huang X, Harder R J, Robinson I K 2014 Opt. Lett. 39 6066
Google Scholar
[11] Odstrčil M, Holler M, Guizar-Sicairos M 2018 Opt. Express 26 12585
Google Scholar
[12] Zhang F, Rodenburg J M 2010 Phys. Rev. B 82 121104
Google Scholar
[13] Zhang F, Chen B, Morrison G R, Vila-Comamala J, Guizar-Sicairos M, Robinson I K 2016 Nat. Commun. 7 13367
Google Scholar
[14] Dong X, Pan X, Liu C, Zhu J 2019 High Power. Laser. Sci. 7 e48
Google Scholar
[15] Pan X, Veetil S, Liu C, Tao H, Jiang Y, Lin Q, Li X, Zhu J 2016 Laser Phys. Lett. 13 055001
Google Scholar
[16] Dong X, Pan X, Liu C, Zhu J 2018 Opt. Lett. 43 1762
Google Scholar
[17] He X, Tao H, Pan X, Liu C, Zhu J 2018 Opt. Express 26 6239
Google Scholar
[18] Haynam C, Wegner P, Auerbach J, Bowers M, Dixit S, Erbert G, Heestand G, Henesian M, Hermann M, Jancaitis K 2007 Appl. Opt. 46 3276
Google Scholar
[19] Tao H, Veetil S P, Cheng J, Pan X, Wang H, Liu C, Zhu J 2015 Appl. Opt. 54 1776
Google Scholar
[20] 柴立群, 于瀛洁, 石琦凯, 许乔, 温圣林, 侯晶 2010 中国激光 37 809
Google Scholar
Chai L Q, Yu Y J, Shi Q K, Xu Q, Wen S L, Hou J 2010 Chin. J. Las. 37 809
Google Scholar
下载:
计量
- 文章访问数: 8521
- PDF下载量: 212
- 被引次数: 0
