-
为了让摩尔定律能够延续下去, 降低功耗是很多研究者关注的问题, 铁电负电容效应的发现为其提供了一种解决方案. 应变工程作为调控铁电薄膜物理性能的有效手段已经被广泛研究. 但是应变对铁电负电容调控的相关机理并不清楚. 本文通过Landau-Khalatnikov方程模拟了应变场和温度场对PbZr0.2Ti0.8O3铁电薄膜负电容的影响. 研究表明, 瞬态负电容的产生伴随着极化的翻转, 在一定温度下压应变有助于铁电负电容的稳定, 而在张应变下铁电极化翻转较快, 负电容效应持续时间较短. 但是, 增加的压应变会导致对应的矫顽电压增大, 需要更大的外电压才能使极化翻转, 从而产生负电容. 此外, 在恒定的应变下, 温度越低, 负电容效应越显著. 本工作对未来负电容微纳器件的设计具有一定的指导意义.In order to continue Moore’s Law, the reducing of power consumption is concerned by many researchers, and the discovery of ferronegative negative capacitance effect (NCE) provides a solution. Strain engineering has been widely studied as an effective means to regulate the physical properties of ferroelectric thin films. But the relevant mechanism of strain to ferroelectric negative capacitance regulation is not clear. Recently, the experimental results have shown that it is possible to stabilize the transient NCE in resistance-ferroelectric networks. In this work, we use the Landau-Khalatnikov theory to study the microscopic domain evolution and the influence of strain and temperature on NCE in a ferroelectric film. It is shown that compressive strain enhances NCE while NCE becomes weaker under a tensile strain. However, a larger compressive strain will give rise to a higher coercive voltage that hinders the NCE from forming. In addition, under a certain strain, the NCE becomes stronger at lower temperature. This work provides the theoretical basis for designing the negative capacitance devices and scaling towards nanoscale dimensions in future.
[1] Moore G 1965 Electronics 38 114
Google Scholar
[2] Waldrop M 2016 Nature 530 144
Google Scholar
[3] Tu L, Wang X, Wang J, Meng X, Chu J 2018 Adv. Electron. Mater. 4 1800231
Google Scholar
[4] Zhirnov V, Cavin R 2008 Nat. Nanotechnol. 3 77
Google Scholar
[5] Salahuddin S, Datta S 2008 Nano Lett. 8 405
Google Scholar
[6] Meindl J, Chen Q, Davis J 2001 Science 293 2044
Google Scholar
[7] Khan A, Chatterjee K, Wang B, Drapcho S, Long Y, Serrao C, Bakaul S, Ramesh R, Salahuddin S 2015 Nat. Mater. 14 182
Google Scholar
[8] Khan A, Hoffmann M, Chatterjee K, Lu Z, Xu R, Serrao C, Smith S, Martin L, Hu C, Ramesh R, Salahuddin S 2017 Appl. Phys. Lett. 111 253501
Google Scholar
[9] Hoffmann M, Pesic M, Chatterjee K, Khan A I, Salahuddin S, Slesazeck S, Schroeder U, Mikolajick T 2016 Adv. Funct. Mater. 26 8643
Google Scholar
[10] Hoffmann M, Khan A, Serrao C, Lu Z, Salahuddin S, Pesic M, Slesazeck S, Schroeder U, Mikolajick T 2018 J. Appl. Phys. 123 184101
Google Scholar
[11] Zhou J, Han G, Li Q, Peng Y, Lu X, Zhang C, Zhang J, Sun Q, Zhang D, Hao Y 2016 IEEE International Electron Devices Meeting San Francisco, CA, USA, December 3–7, 2016 p16651211
[12] Arimoto Y, Ishiwara H 2004 MRS Bull. 29 823
Google Scholar
[13] Tanaka K, Kubota T, Sakabe Y 2002 Sens. Actuators, A 96 179
Google Scholar
[14] Hoshyarmanesh H, Ghodsi M, Kim M, Cho H, Park H 2019 Sensors 19 2805
Google Scholar
[15] Rath M, Varadarajan E, Premkumar S, Shinde S, Natarajan V, Rao R 2019 Ferroelectrics 551 17
Google Scholar
[16] Janolin P 2009 J. Mater. Sci. 44 5025
Google Scholar
[17] Choi K, Biegalski M, Li Y, Sharan A, Schubert J, Uecker R, Peiche P, Chen Y, Pan X, Gopalan V, Chen L, Schlom D, Eom C 2004 Science 306 1005
Google Scholar
[18] Sharma A, Ban Z, Alpay S 2004 J. Appl. Phys. 95 3618
Google Scholar
[19] Pertsev N, Zembilgotov A, Tagantsev A K 1998 Phys. Rev. Lett. 80 1988
Google Scholar
[20] Pertsev N, Zembilgotov A, Tagantsev A 1999 Ferroelectrics 223 79
Google Scholar
[21] Ban Z, Alpay S 2002 J. Appl. Phys. 91 9288
Google Scholar
[22] Ban Z, Alpay S 2003 J. Appl. Phys. 93 504
Google Scholar
[23] Pertsev N, Kukhar V, Kohlstedt H, Waser R 2003 Phys. Rev. B 67 054107
Google Scholar
[24] Guo R, You L, Zhou Y, Lim Z, Zou X, Chen L, Ramesh R, Wang J 2013 Nat. Commun. 4 1990
Google Scholar
[25] Chang S, Avci U, Nikonov D, Manipatruni S, Young I 2018 Phys. Rev. Appl. 9 014010
Google Scholar
[26] Hoffmann M, Fengler F, Herzig M, Mittmann T, Max B, Schroeder U, Negrea R, Lucian P, Slesazeck S, Mikolajick T 2019 Nature 565 464
Google Scholar
[27] Lo V 2003 J. Appl. Phys. 94 3353
Google Scholar
[28] Zhang W, Bhattacharya K 2005 Acta Mater. 53 185
Google Scholar
[29] Rabe K, Ahn C, Triscone J 2007 Physics of Ferroelectrics (Berlin Heidelberg: Springer-Verlag) pp366–368
[30] Haun M, Zhuang Z, Furman E 1989 Ferroelectrics 99 45
Google Scholar
[31] Qiu Q, Alpay S, Nagarajan V 2010 J. Appl. Phys. 107 114105
[32] Liu C, Wang J 2021 Acta Mater. 206 116607
Google Scholar
[33] Pertsev N, Contreras J, Kukhar V, Hermanns B, Kohlstedt H, Waser R 2003 Appl. Phys. Lett. 83 3356
Google Scholar
-
图 1 铁电负电容瞬态响应模型及其等效电路图
Fig. 1. Transient response model of ferroelectric negative capacitance and its equivalent circuit diagram.
图 2 (a)在T = 300 K, Sm = –0.011, 外加脉冲
$ {V_{\text{S}}} = 14\;{\text{V}} $ 下$ {V_{\text{f}}} $ 与时间t的局部关系图; (b)—(f)不同时间段的铁电极化分布($ t = 0.545 $ ,$ 4.85 $ ,$ 11.0 $ ,$ 14.3 $ ,$16.5\;{\text{μ} }{\rm{ s}}$ )Fig. 2. (a) Local relationship diagram with time under applied pulse; (b)–(f) ferroelectric polarization distribution in different time periods (
$ t = 0.545 $ ,$ 4.85 $ ,$ 11.0 $ ,$ 14.3 $ ,$16.5\;{\text{μ} }{\rm{ s}}$ ).
图 3 恒定应变
$ {S_{\text{m}}} = 0.011 $ 以及不同温度下, (a), (c), (e)外加电压$ {V_{\text{S}}} = 14\;{\text{V}} $ 时铁电材料PbZr0.2Ti0.8O3的${V_{\text{f}}} \text{-} t$ 关系图、${i_{\rm R}} \text{-} t$ 关系图、${Q_{\text{f}}} \text{-} t$ 关系图; (b), (d), (f)外加电压$ {V_{\text{S}}} = 10\;{\text{V}} $ 时铁电材料PbZr0.2Ti0.8O3的${V_{\text{f}}} \text{-} t$ 关系图、${i_{\rm R}} \text{-} t$ 关系图、${Q_{\text{f}}} \text{-} t$ 关系图Fig. 3. Under constant strain
$ {S_{\text{m}}} = 0.011 $ and different temperatures, (a), (c), (e) the${V_{\text{f}}}\text{-} t$ relationship diagram,${i_{\rm R}} \text{-} t$ relationship diagram and${Q_{\text{f}}} \text{-} t$ relationship diagram of ferroelectric materials PbZr0.2Ti0.8O3 when the applied voltage$ {V_{\text{S}}} = 14\;{\text{V}} $ , respectively; (b), (d), (f) the${V_{\text{f}}} \text{-} t$ relationship diagram,${i_{\rm R}} \text{-} t$ relationship diagram and${Q_{\text{f}}} \text{-} t$ relationship diagram of ferroelectric materials PbZr0.2Ti0.8O3 when the applied voltage$ {V_{\text{S}}} = 10\;{\text{V}} $ , respectively.
图 4 恒定温度
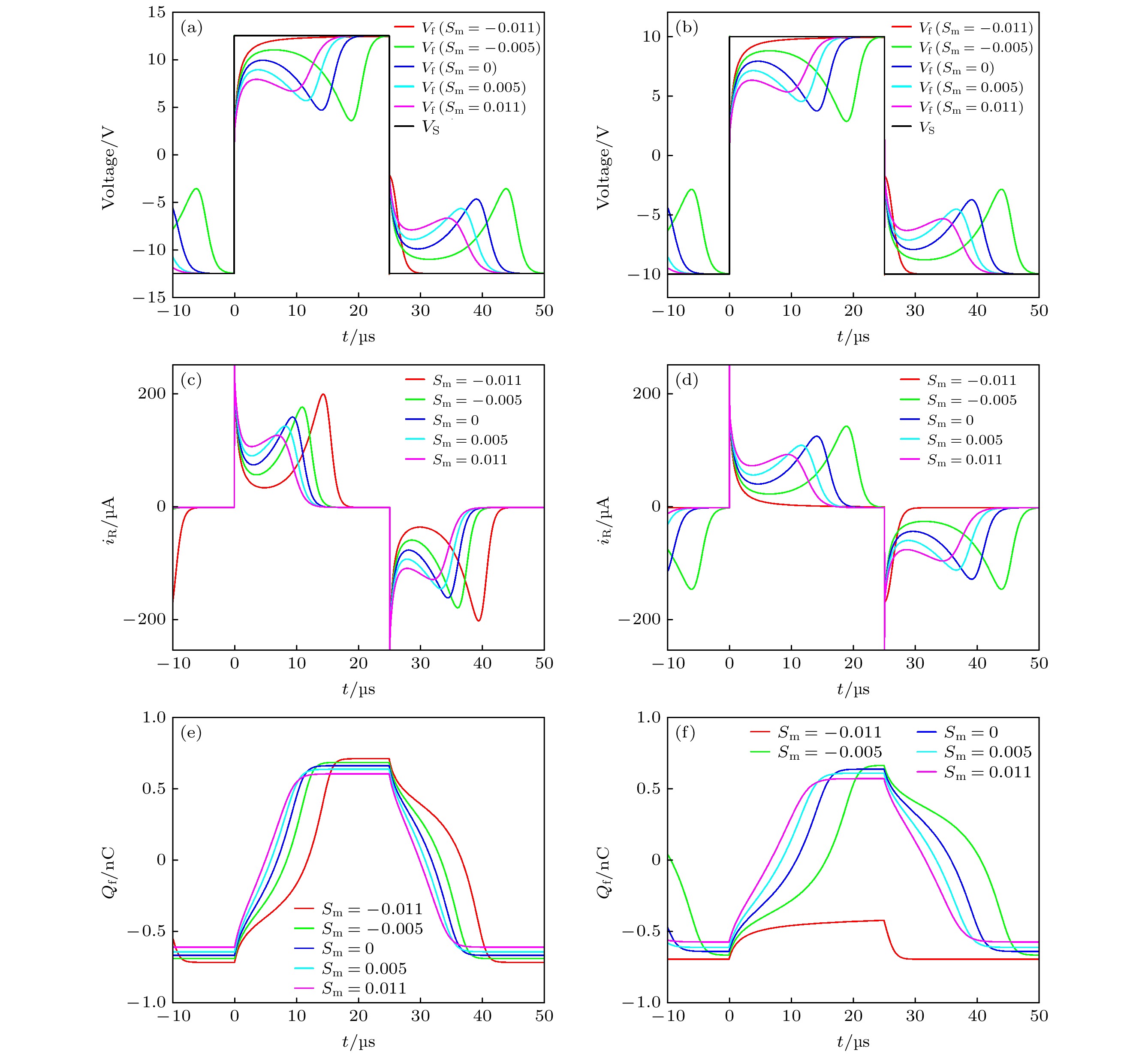
$ T = 300\;{\text{K}} $ 以及不同应变下, (a), (c), (e)外加电压$ {V_{\text{S}}} = 14\;{\text{V}} $ 时铁电材料PbZr0.2Ti0.8O3的${V_{\text{f}}} \text{-} t$ 关系图、${i_{\rm R}} \text{-} t$ 关系图、${Q_{\text{f}}} \text{-} t$ 关系图; (b), (d), (f)外加电压$ {V_{\text{S}}} = 10\;{\text{V}} $ 时铁电材料PbZr0.2Ti0.8O3的${V_{\text{f}}} \text{-} t$ 关系图、${i_{\rm R}} \text{-} t$ 关系图、${Q_{\text{f}}} \text{-} t$ 关系图Fig. 4. Under constant temperature
$ T = 300\;{\text{K}} $ and different strains, (a), (c), (e) the${V_{\text{f}}} \text{-} t$ relationship diagram,${i_{\rm R}} \text{-} t$ relationship diagram and${Q_{\text{f}}} \text{-} t$ relationship diagram of ferroelectric materials PbZr0.2Ti0.8O3 when the applied voltage$ {V_S} = 14\;{\text{V}} $ , respectively; (b), (d), (f) the${V_{\text{f}}} \text{-} t$ relationship diagram,${i_{\rm R}} \text{-} t$ relationship diagram and${Q_{\text{f}}} \text{-} t$ relationship diagram of ferroelectric materials PbZr0.2Ti0.8O3 when the applied voltage$ {V_{\text{S}}} = 10\;{\text{V}} $ , respectively.
图 5 自由能U与极化P的关系图 (a)恒定应变
$ {S_{\text{m}}} = 0.011 $ , 不同温度下$U \text{-} P$ 图; (b)恒温$ T = 300\;{\text{K}} $ , 不同应变下$U \text{-} P$ 图Fig. 5. Relationship between free energy U and polarization P: (a)
$U\text{-} P$ diagram with constant strain$ {S_{\text{m}}} = 0.011 $ at different temperatures; (b)$U \text{-} P$ diagram with constant temperature$ T = 300\;{\text{K}} $ at different strains.表 1 PbZr0.2Ti0.8O3材料的相关系数(温度T的单位为K)
Table 1. Correlation coefficient of PbZr0.2Ti0.8O3 material (The unit of temperature T is K).
Coefficients PbZr0.2Ti0.8O3 Units Reference a1 3.44(T – 729.5) 105 C–2·m2·N [29] a11 –3.050 107 C–4·m6·N [29] a111 2.475 108 C–6·m10·N [29] s11 8.2 10–12 m2/N [29] s12 –2.6 10–12 m2/N [29] Q12 –0.0245 m4/C2 [30] $ {t_{{\text{FE}}}} $ 60 nm [7] A 302 ${\text{μ}}{ {\text{m} }^2}$ [7] R 50 ${\rm{k } }\Omega$ [7] k $ 1.26 \times {10^{ - 7}} $ $ {{\text{m}}^3}/{\text{F}} $ ${\rho{'} }$ 70 ${\rm{k } }\Omega$ $ \Delta x $ $ 150 $ $ {\text{nm}} $ $ \Delta y $ $ 150 $ $ {\text{nm}} $ $ {N_x} $ 200 $ {N_y} $ 200 $ \Delta t $ $ 5 $ $ {\text{ns}} $ 
下载: 导出CSV
-
[1] Moore G 1965 Electronics 38 114
Google Scholar
[2] Waldrop M 2016 Nature 530 144
Google Scholar
[3] Tu L, Wang X, Wang J, Meng X, Chu J 2018 Adv. Electron. Mater. 4 1800231
Google Scholar
[4] Zhirnov V, Cavin R 2008 Nat. Nanotechnol. 3 77
Google Scholar
[5] Salahuddin S, Datta S 2008 Nano Lett. 8 405
Google Scholar
[6] Meindl J, Chen Q, Davis J 2001 Science 293 2044
Google Scholar
[7] Khan A, Chatterjee K, Wang B, Drapcho S, Long Y, Serrao C, Bakaul S, Ramesh R, Salahuddin S 2015 Nat. Mater. 14 182
Google Scholar
[8] Khan A, Hoffmann M, Chatterjee K, Lu Z, Xu R, Serrao C, Smith S, Martin L, Hu C, Ramesh R, Salahuddin S 2017 Appl. Phys. Lett. 111 253501
Google Scholar
[9] Hoffmann M, Pesic M, Chatterjee K, Khan A I, Salahuddin S, Slesazeck S, Schroeder U, Mikolajick T 2016 Adv. Funct. Mater. 26 8643
Google Scholar
[10] Hoffmann M, Khan A, Serrao C, Lu Z, Salahuddin S, Pesic M, Slesazeck S, Schroeder U, Mikolajick T 2018 J. Appl. Phys. 123 184101
Google Scholar
[11] Zhou J, Han G, Li Q, Peng Y, Lu X, Zhang C, Zhang J, Sun Q, Zhang D, Hao Y 2016 IEEE International Electron Devices Meeting San Francisco, CA, USA, December 3–7, 2016 p16651211
[12] Arimoto Y, Ishiwara H 2004 MRS Bull. 29 823
Google Scholar
[13] Tanaka K, Kubota T, Sakabe Y 2002 Sens. Actuators, A 96 179
Google Scholar
[14] Hoshyarmanesh H, Ghodsi M, Kim M, Cho H, Park H 2019 Sensors 19 2805
Google Scholar
[15] Rath M, Varadarajan E, Premkumar S, Shinde S, Natarajan V, Rao R 2019 Ferroelectrics 551 17
Google Scholar
[16] Janolin P 2009 J. Mater. Sci. 44 5025
Google Scholar
[17] Choi K, Biegalski M, Li Y, Sharan A, Schubert J, Uecker R, Peiche P, Chen Y, Pan X, Gopalan V, Chen L, Schlom D, Eom C 2004 Science 306 1005
Google Scholar
[18] Sharma A, Ban Z, Alpay S 2004 J. Appl. Phys. 95 3618
Google Scholar
[19] Pertsev N, Zembilgotov A, Tagantsev A K 1998 Phys. Rev. Lett. 80 1988
Google Scholar
[20] Pertsev N, Zembilgotov A, Tagantsev A 1999 Ferroelectrics 223 79
Google Scholar
[21] Ban Z, Alpay S 2002 J. Appl. Phys. 91 9288
Google Scholar
[22] Ban Z, Alpay S 2003 J. Appl. Phys. 93 504
Google Scholar
[23] Pertsev N, Kukhar V, Kohlstedt H, Waser R 2003 Phys. Rev. B 67 054107
Google Scholar
[24] Guo R, You L, Zhou Y, Lim Z, Zou X, Chen L, Ramesh R, Wang J 2013 Nat. Commun. 4 1990
Google Scholar
[25] Chang S, Avci U, Nikonov D, Manipatruni S, Young I 2018 Phys. Rev. Appl. 9 014010
Google Scholar
[26] Hoffmann M, Fengler F, Herzig M, Mittmann T, Max B, Schroeder U, Negrea R, Lucian P, Slesazeck S, Mikolajick T 2019 Nature 565 464
Google Scholar
[27] Lo V 2003 J. Appl. Phys. 94 3353
Google Scholar
[28] Zhang W, Bhattacharya K 2005 Acta Mater. 53 185
Google Scholar
[29] Rabe K, Ahn C, Triscone J 2007 Physics of Ferroelectrics (Berlin Heidelberg: Springer-Verlag) pp366–368
[30] Haun M, Zhuang Z, Furman E 1989 Ferroelectrics 99 45
Google Scholar
[31] Qiu Q, Alpay S, Nagarajan V 2010 J. Appl. Phys. 107 114105
[32] Liu C, Wang J 2021 Acta Mater. 206 116607
Google Scholar
[33] Pertsev N, Contreras J, Kukhar V, Hermanns B, Kohlstedt H, Waser R 2003 Appl. Phys. Lett. 83 3356
Google Scholar
下载:
计量
- 文章访问数: 4031
- PDF下载量: 79
- 被引次数: 0
