-
CdS/CdMnTe异质结是具有集成分立光谱结构的叠层电池的“核芯”元件, 是驱动第三代太阳能电池发展的核心引擎, 其界面相互作用对大幅度提高太阳能电池的转换效率至关重要. 本文采用基于密度泛函理论的第一性原理计算构建CdS (002), CdMnTe (111)表面模型及Mn原子占据不同位置的CdS/CdMnTe异质结界面结构模型, 分析CdS (002), CdMnTe (111)表面及异质结界面的电子性质和光学性质. 晶格结构分析表明, CdS/CdMnTe异质结的晶格失配度约为3.5%, 弛豫后原子位置与键长均在界面处发生一定程度的变化. 态密度分析发现异质结界面的费米能级附近不存在界面态, 并且界面处的Cd, S, Te原子之间的轨道杂化可增强界面的结合能力. 差分电荷密度分析显示, 界面处发生了电荷的重新分配, 电子由CdMnTe转移到CdS侧. 光学分析显示, CdS/CdMnTe异质结主要吸收紫外光, 吸收系数可达105 cm–1, 但不同Mn原子位置的异质结光学性质也稍有差别. 在200—250 nm范围, Mn原子位于中间层的异质结的吸收系数更大, 但在250—900 nm范围内, Mn原子位于界面层的异质结吸收峰更高. 本文合理构建了CdS/CdMnTe异质结模型, 计算分析了其界面光电性能, 可为提高叠层电池的光电转换效率提供一定的理论参考, 为实现多带隙异质结的实验研究提供一定的理论依据.
-
关键词:
- CdS/CdMnTe异质结 /
- 第一性原理计算 /
- 态密度 /
- 光学性质
CdS/CdMnTe heterojunction is the core of photoelectric conversion of CdMnTe film solar cells, whose interface properties have an important influence on the cell efficiency. In this study, the first-principles calculation method based on density functional theory is used to build the surface model for each of the CdS (002) and the CdMnTe (111) and the model of CdS/CdMnTe heterojunction with Mn atoms occupying different positions, and to analyze their electronic properties and optical properties. The results show that the lattice mismatch of the CdS/CdMnTe heterojunction is about 3.5%, the atomic positions and bond lengths of the interface change slightly after relaxation. The density of states shows that there is no interface state near the Fermi level in CdS/CdMnTe interface. Besides, the atoms at CdS/CdMnTe interface are hybridized, which can enhance the interface bonding. The differential charge density analyses indicate that the charge transfer mainly occurs at the interface, and electrons transfer from CdMnTe to CdS. The optical analysis shows that CdS/CdMnTe heterojunction mainly absorbs ultraviolet light, and the absorption coefficient can reach 105 cm–1. However, the optical properties of heterojunctions with different Mn atom positions are slightly different. In a range of 200–250 nm, the absorption coefficient of the heterojunction with Mn atom in the middle layer is larger, but in a range of 250–900 nm, the absorption peak of the heterojunction with Mn atom in the interface layer is higher. The results in this paper can provide some references for improving the photoelectric conversion efficiency of stacked solar cells through the reasonable construction of the heterojunction model and the analysis of the interface photoelectric performance, which is beneficial to the experimental research of multi-band gap heterojunction.-
Keywords:
- CdS/CdMnTe heterojunction /
- first-principles /
- density of states /
- optical properties
[1] 朱建国, 孙小松, 李卫 2007 电子与光电子材料 (北京: 国防工业出版社) 第125页
Zhu J G, Sun X S, Li W 2007 Electronic and Optoelectronic Materials (Beijing: Defense Industry Press) p125 (in chinese)
[2] Miles R W, Hynes K M, Forbes I 2005 Prog. Cryst. Growth Charact. Mater. 51 1
Google Scholar
[3] Mishima T, Taguchi M, Sakata H, Maruyama E 2011 Sol. Energy Mater. Sol. Cells 95 18
Google Scholar
[4] Jordan D, Nagle J P 1994 Prog. Photovoltaics 2 171
Google Scholar
[5] Cheng Y J, Yang S H, Hsu C S 2009 Chem. Rev. 109 5868
Google Scholar
[6] Mora-Seró I, Bisquert J 2010 J. Phys. Chem. Lett. 1 3046
Google Scholar
[7] Zhao J 2004 Sol. Energy Mater. Sol. Cells 82 53
Google Scholar
[8] Cojocaru-Miredin O, Choi P, Wuerz R, Raabe D 2011 Appl. Phys. Lett. 98 73
Google Scholar
[9] Yang L, Xuan Y, Tan J 2011 Opt. Express 19 A1165
Google Scholar
[10] Chopra K L, Paulson P D, Dutta V 2004 Prog. Photovoltaics 12 69
Google Scholar
[11] Zhang K, Guo H 2017 J. Mater. Sci. Mater. Electron. 28 17044
Google Scholar
[12] Wu X 2004 Sol. Energy 77 803
Google Scholar
[13] Chander S, De A K, Dhaka M S 2018 Sol. Energy 174 757
Google Scholar
[14] Chander S, Dhaka M S 2016 Phys. E 84 112
Google Scholar
[15] Lee S H, Gupta A, Wang S, Compaan A D, McCandless B E 2005 Sol. Energy Mater. Sol. Cells 86 551
Google Scholar
[16] Chander S, Dhaka M S 2019 Sol. Energy 183 544
Google Scholar
[17] Rohatgi A, Ringel S A, Welch J, Meeks E, Pollard K, Erbil A, Summers C J, Meyers P V 1988 Sol. Energy 24 185
[18] Luan L J, Gao L, Lv H H, Yu P F, Wang T, He Y, Zheng D 2020 Sci. Rep. 10 1
Google Scholar
[19] Wang S L, Lee S H, Gupta A 2004 MRS Proc. 836 L5.39
Google Scholar
[20] 侯泽荣, 万磊, 白治中, 王德亮 2010 中国科学技术大学学报 40 718
Google Scholar
Hou Z R, W L, Bai Z Z, Wang D L 2010 J. Univ. Sci. Tech. Chin. 40 718
Google Scholar
[21] Olusola O I, Madugu M L, Ojo A A, Dharmadasa I M 2020 J. Mater. Sci. Mater. Electron. 31 22151
Google Scholar
[22] Shafaay B A 2014 J. Chem., Biol. Phys. Sci. 4 1
[23] Gueddim A, Madjet M E, Zerroug S, Bouarissa N 2016 Opt. Quantum Electron. 48 551
Google Scholar
[24] Llchuk H, Zmiiovska E, Petrus R, Semkive I, Lopatynskyi I, Kashuba 2020 J. Nano-Electron. Phys. 12 01027
Google Scholar
[25] Cao A, Tan T T, Zhang H, Du Y, Sun Y, Zha G 2018 Phys. B 545 323
Google Scholar
[26] Merad A, Kanoun M, Merad G, Cibert J, Aourag H 2005 Mater. Chem. Phys. 92 333
Google Scholar
[27] Liu H X, Tang F L, Xue H T, Zhang Y, Cheng Y W, Feng Y D 2016 Chin. Phys. B 25 123101
Google Scholar
[28] Shenoy S, Tarafder K 2020 J. Phys. Condens. Matter 32 275501
Google Scholar
[29] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
Google Scholar
[30] Shi L B, Xu C Y, Yuan H K 2011 Phys. B 406 3187
Google Scholar
[31] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[32] Butler K T, Frost J M, Walsh A 2015 Mater. Horiz. 2 228
Google Scholar
[33] Wang J S, Tong S C, Tsai Y H, Tsai W J, Yang C S, Chang Y H, Shen J L 2015 J. Alloys Compd. 646 129
Google Scholar
[34] Kumar S G, Rao K S R K 2014 Energy Environ. Sci. 7 45
Google Scholar
[35] Cheng Y W, Tang F L, Xue H T, Liu H X, Gao B, Feng Y D 2016 Mater. Sci. Semicond. Process. 45 9
Google Scholar
[36] Momma K, Izumi F 2008 J. Appl. Crystallogr. 41 653
Google Scholar
[37] Guo Y, Xue Y, Geng C, Li C, Li X, Niu Y 2019 J. Phys. Chem. C 123 16075
Google Scholar
[38] Yin W J, Shi T, Yan Y 2015 J. Phys. Chem. C 119 5253
Google Scholar
[39] Scharber M C, Mühlbacher D, Koppe M, Denk P, Waldauf C, Heeger A J, Brabec C J 2006 Adv. Mater. 18 789
Google Scholar
[40] Sharma S, Devi N, Verma U P, RajaRam P 2011 Phys. B 406 4547
Google Scholar
[41] Dadsetani M, Pourghazi A 2006 Phys. Rev. B 73 195102
Google Scholar
[42] Gajdos M, Hummer K, Kresse G, Furthmueller J, Bechstedt F 2006 Phys. Rev. B 73 045112
Google Scholar
-
图 1 表面模型的建立 (a) CdS (002)表面模型; (b) CdMnTe (111)-A1表面模型; (c) CdMnTe (111)-B1表面模型
Fig. 1. Building of the surface models: (a) Model of the CdS (002) surface; (b) A1 surface model of CdMnTe (111); (c) B1 surface model of CdMnTe (111).
图 2 弛豫后的表面原子位置和层间距离的变化 (a) CdS (002)表面模型; (b) CdMnTe (111)-A1表面模型; (c) CdMnTe (111)-B1表面模型
Fig. 2. Variations of atomic positions and interlayer spacing after relaxation: (a) Model of the CdS (002) surface; (b) A1 surface model of CdMnTe (111); (c) B1 surface model of CdMnTe (111).
图 3 表面模型总态密度和第1层及第5层局域态密度 (a) CdS (002); (b) CdMnTe (111)-A1; (c) CdMnTe (111)-B1
Fig. 3. Total density of states and the local density of states of the first layer and the fifth layer: (a) CdS (002); (b) A1 of CdMnTe (111); (c) B1 of CdMnTe (111).
图 4 CdS/CdMnTe异质结模型 (a) Mn原子位于界面层的异质结模型(模型A2); (b) Mn原子位于中间层的异质结模型(模型B2)
Fig. 4. CdS/CdMnTe heterojunction models: (a) Mn atom being in the interface layer (model A2); (b) Mn atom in the internal layer (model B2).
图 5 模型A2和B2的总能量随界面间距的变化
Fig. 5. Variation of total energy dependent on the interface distance of the models A2 and B2, respectively.
图 6 弛豫前后界面及其附近原子键长的变化 (a)弛豫前的模型A2; (b)弛豫后的模型A2; (c)弛豫前的模型B2; (d)弛豫后的模型B2
Fig. 6. Bond lengths in/near of the interface before and after relaxation: (a) Before relaxation of A2; (b) after relaxation of A2; (c) before relaxation of B2; (d) after relaxation of B2.
图 7 CdS/CdMnTe异质结总态密度与局域态密度 (a)模型A2; (b)模型B2
Fig. 7. Total density of states and local density of states of the CdS/CdMnTe heterojunction: (a) Model A2; (b) model B2.
图 8 CdS/CdMnTe异质结界面处原子的分态密度 (a)模型A2; (b)模型B2
Fig. 8. Part density of states of different atoms in the CdS/CdMnTe interface: (a) Model A2; (b) model B2.
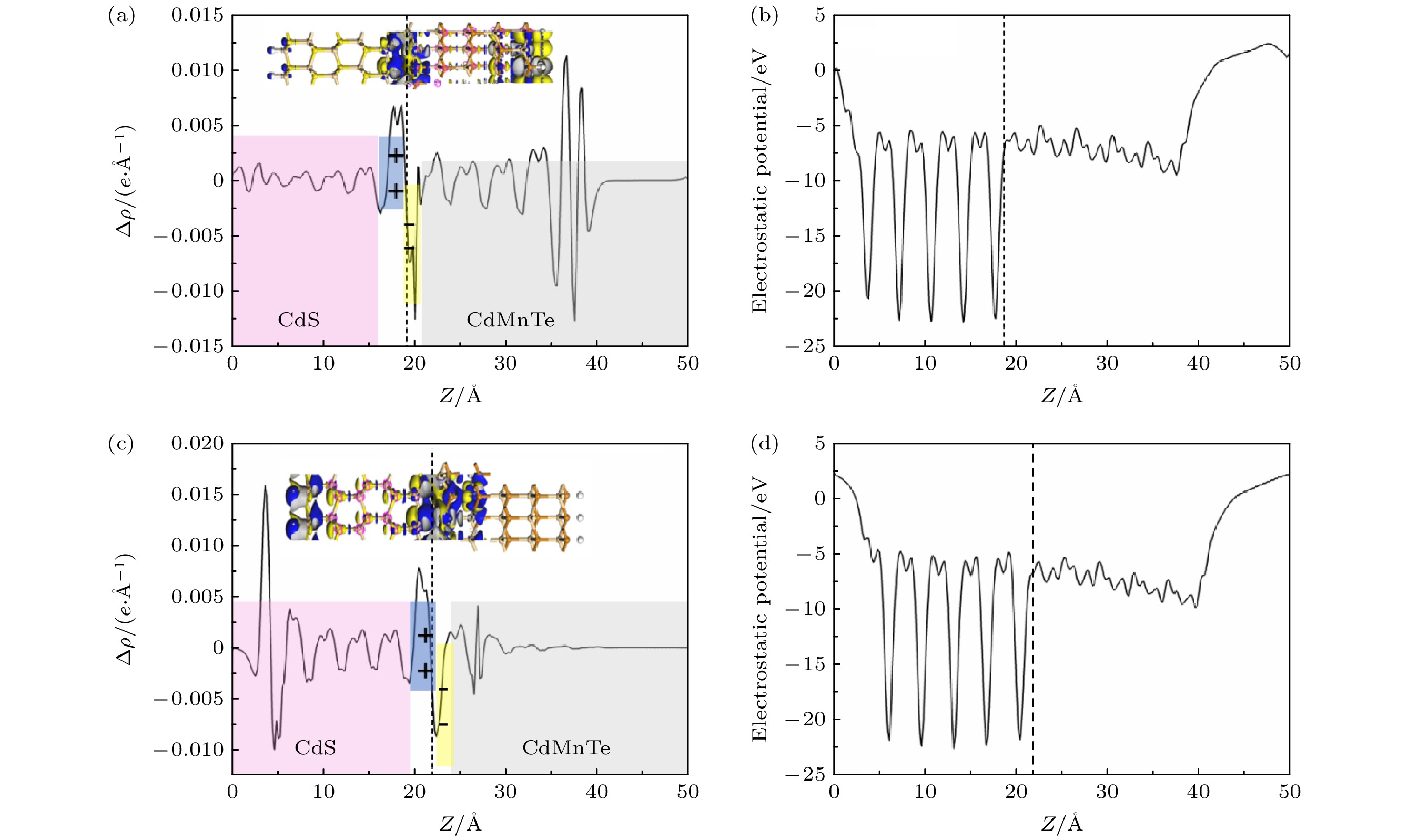
图 9 电荷重新分布图 (a), (c)异质结A2与B2的差分电荷示意图和相应平面差分电荷密度曲线, 黄色区域代表电荷消耗, 蓝色区域代表电荷积累, 等值面值为0.00103 e/Å3; (b), (d) A2与B2沿z轴方向的平均静电势
Fig. 9. Distribution diagram of charges: (a), (c) Charge density difference and the corresponding planar differential charge density curve of the A2 model and B2 model, respectively. The yellow region represents charge depletion, the bule region indicates charge accumulation, the isosurface value is 0.00103 e/Å3. (b), (d) the average electrotactic potential difference of the A2 model and B2 model, respectively, along the direction of z axis.
图 10 表面模型和异质结模型的吸收光谱 (a) CdS (002), CdMnTe (111)-B1表面和异质结B2模型; (b)异质结A2和B2模型
Fig. 10. Absorption spectra of surface models and heterojunction models: (a) Surface CdS (002), surfaces of CdMnTe (111)-B1, and B2 model of CdMnTe/CdS heterojunction model; (b) heterojunction A2 model and B2 model.
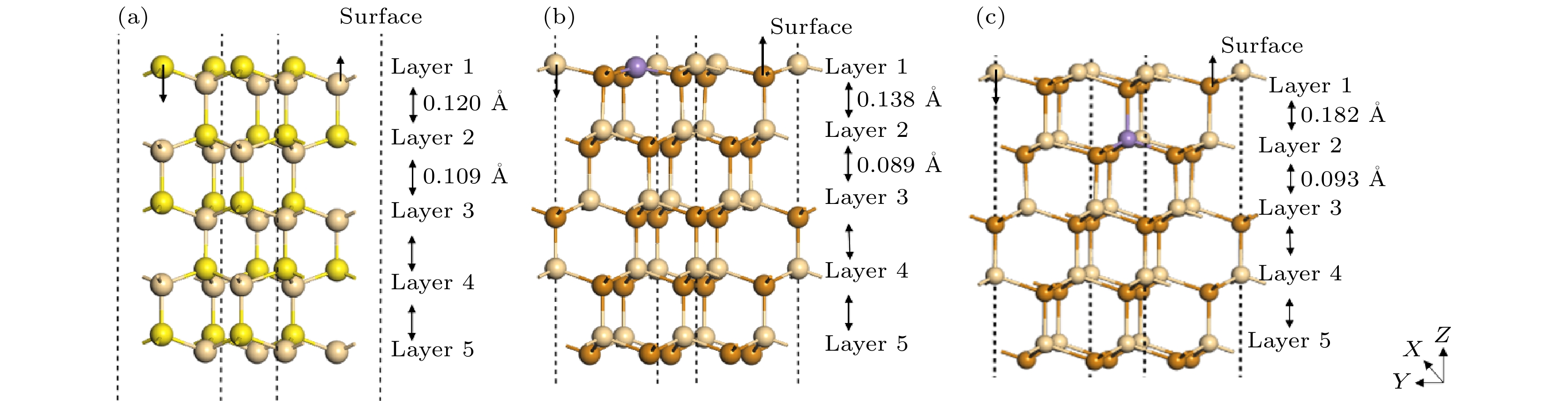
表 2 弛豫后CdMnTe (111)和CdS (002)表面层间距离的变化
Table 2. Variations of interlayer spacing of CdMnTe (111) and CdS (002) surfaces after relaxation.
Surface items d1-2/Å d2-3/Å d3-4/Å d4-5/Å CdMnTe-A1 dCd-Te 2.829 2.837 2.831 2.831 dMn-Te 2.605 ∆d 0.138 0.089 0.000 0.000 CdMnTe-B1 dCd-Te 2.791 2.841 2.831 2.831 dMn-Te 2.697 ∆d 0.182 0.093 0.000 0.000 CdS dCd-S 2.534 2.538 2.536 2.536 ∆d 0.120 0.109 0.000 0.000 
下载: 导出CSV
-
[1] 朱建国, 孙小松, 李卫 2007 电子与光电子材料 (北京: 国防工业出版社) 第125页
Zhu J G, Sun X S, Li W 2007 Electronic and Optoelectronic Materials (Beijing: Defense Industry Press) p125 (in chinese)
[2] Miles R W, Hynes K M, Forbes I 2005 Prog. Cryst. Growth Charact. Mater. 51 1
Google Scholar
[3] Mishima T, Taguchi M, Sakata H, Maruyama E 2011 Sol. Energy Mater. Sol. Cells 95 18
Google Scholar
[4] Jordan D, Nagle J P 1994 Prog. Photovoltaics 2 171
Google Scholar
[5] Cheng Y J, Yang S H, Hsu C S 2009 Chem. Rev. 109 5868
Google Scholar
[6] Mora-Seró I, Bisquert J 2010 J. Phys. Chem. Lett. 1 3046
Google Scholar
[7] Zhao J 2004 Sol. Energy Mater. Sol. Cells 82 53
Google Scholar
[8] Cojocaru-Miredin O, Choi P, Wuerz R, Raabe D 2011 Appl. Phys. Lett. 98 73
Google Scholar
[9] Yang L, Xuan Y, Tan J 2011 Opt. Express 19 A1165
Google Scholar
[10] Chopra K L, Paulson P D, Dutta V 2004 Prog. Photovoltaics 12 69
Google Scholar
[11] Zhang K, Guo H 2017 J. Mater. Sci. Mater. Electron. 28 17044
Google Scholar
[12] Wu X 2004 Sol. Energy 77 803
Google Scholar
[13] Chander S, De A K, Dhaka M S 2018 Sol. Energy 174 757
Google Scholar
[14] Chander S, Dhaka M S 2016 Phys. E 84 112
Google Scholar
[15] Lee S H, Gupta A, Wang S, Compaan A D, McCandless B E 2005 Sol. Energy Mater. Sol. Cells 86 551
Google Scholar
[16] Chander S, Dhaka M S 2019 Sol. Energy 183 544
Google Scholar
[17] Rohatgi A, Ringel S A, Welch J, Meeks E, Pollard K, Erbil A, Summers C J, Meyers P V 1988 Sol. Energy 24 185
[18] Luan L J, Gao L, Lv H H, Yu P F, Wang T, He Y, Zheng D 2020 Sci. Rep. 10 1
Google Scholar
[19] Wang S L, Lee S H, Gupta A 2004 MRS Proc. 836 L5.39
Google Scholar
[20] 侯泽荣, 万磊, 白治中, 王德亮 2010 中国科学技术大学学报 40 718
Google Scholar
Hou Z R, W L, Bai Z Z, Wang D L 2010 J. Univ. Sci. Tech. Chin. 40 718
Google Scholar
[21] Olusola O I, Madugu M L, Ojo A A, Dharmadasa I M 2020 J. Mater. Sci. Mater. Electron. 31 22151
Google Scholar
[22] Shafaay B A 2014 J. Chem., Biol. Phys. Sci. 4 1
[23] Gueddim A, Madjet M E, Zerroug S, Bouarissa N 2016 Opt. Quantum Electron. 48 551
Google Scholar
[24] Llchuk H, Zmiiovska E, Petrus R, Semkive I, Lopatynskyi I, Kashuba 2020 J. Nano-Electron. Phys. 12 01027
Google Scholar
[25] Cao A, Tan T T, Zhang H, Du Y, Sun Y, Zha G 2018 Phys. B 545 323
Google Scholar
[26] Merad A, Kanoun M, Merad G, Cibert J, Aourag H 2005 Mater. Chem. Phys. 92 333
Google Scholar
[27] Liu H X, Tang F L, Xue H T, Zhang Y, Cheng Y W, Feng Y D 2016 Chin. Phys. B 25 123101
Google Scholar
[28] Shenoy S, Tarafder K 2020 J. Phys. Condens. Matter 32 275501
Google Scholar
[29] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
Google Scholar
[30] Shi L B, Xu C Y, Yuan H K 2011 Phys. B 406 3187
Google Scholar
[31] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[32] Butler K T, Frost J M, Walsh A 2015 Mater. Horiz. 2 228
Google Scholar
[33] Wang J S, Tong S C, Tsai Y H, Tsai W J, Yang C S, Chang Y H, Shen J L 2015 J. Alloys Compd. 646 129
Google Scholar
[34] Kumar S G, Rao K S R K 2014 Energy Environ. Sci. 7 45
Google Scholar
[35] Cheng Y W, Tang F L, Xue H T, Liu H X, Gao B, Feng Y D 2016 Mater. Sci. Semicond. Process. 45 9
Google Scholar
[36] Momma K, Izumi F 2008 J. Appl. Crystallogr. 41 653
Google Scholar
[37] Guo Y, Xue Y, Geng C, Li C, Li X, Niu Y 2019 J. Phys. Chem. C 123 16075
Google Scholar
[38] Yin W J, Shi T, Yan Y 2015 J. Phys. Chem. C 119 5253
Google Scholar
[39] Scharber M C, Mühlbacher D, Koppe M, Denk P, Waldauf C, Heeger A J, Brabec C J 2006 Adv. Mater. 18 789
Google Scholar
[40] Sharma S, Devi N, Verma U P, RajaRam P 2011 Phys. B 406 4547
Google Scholar
[41] Dadsetani M, Pourghazi A 2006 Phys. Rev. B 73 195102
Google Scholar
[42] Gajdos M, Hummer K, Kresse G, Furthmueller J, Bechstedt F 2006 Phys. Rev. B 73 045112
Google Scholar
下载:
计量
- 文章访问数: 7153
- PDF下载量: 224
- 被引次数: 0
