-
基于SSH (Su-Schriffer-Heeger)哈密顿的非绝热分子动力学方法广泛应用于模拟有机共轭聚合物中光激发过程和极化子运动. 目前, 该方法中电子波函数的演化是在透热表象中进行的, 本文对该方法进行扩展, 让电子波函数的演化在绝热表象下进行, 给出了详细的公式推导过程. 分别利用新、旧方法模拟了一条共轭聚合物链中光激发动力学过程, 两种方法得到的数值计算结果相符. 新方法可以加深对非绝热分子动力学方法的理解, 提供激发态弛豫过程中不同分子轨道之间非绝热耦合强度等重要信息.
-
关键词:
- 非绝热分子动力学 /
- 绝热表象 /
- 共轭聚合物 /
- Su-Schriffer-Heeger模型
In this paper, we develop a nonadiabatic molecular dynamics method based on Su-Schriffer-Heeger (SSH) Hamiltonian, and this method is widely used to study the photoexcitation dynamics and polaron motion in conjugated polymers. However, in this method, the time-dependent Schrödinger equation has so far been solved in a diabatic representation, also known as site representation. In order to provide a deeper insight into the nonadiabatic molecular dynamics method, we solve the time-dependent Schrödinger equation in an adiabatic representation. The new method can directly provide the important information about the strength of nonadiabatic couplings between different molecular orbitals in the excited-state relaxation process, helping us to predict the electron and energy transfer within or between polymer chains. Solving the time-dependent Schrödinger equation in an adiabatic representation is much more complicated, it is mainly because we need to calculate the nonadiabatic couplings between different molecular orbitals. In this paper, the detailed formula derivation and actual calculation process of the nonadiabatic molecular dynamics method in an adiabatic representation are given. Using this new method, we simulate three photoexcitation processes in a conjugated polymer chain, HOMO→LUMO, HOMO–1→LUMO+1 and HOMO–2→LUMO+2. We analyze in detail the time evolutions of lattice configuration for these three photoexcitation processes, and compare these results with those obtained by diabatic representation (site representation) showing that the results obtained from these two representations are consistent with each other. -
Keywords:
- nonadiabatic molecular dynamics /
- adiabatic representation /
- conjugated polymer /
- Su-Schriffer-Heeger model
[1] Stafström S 2010 Chem. Soc. Rev. 39 2484
Google Scholar
[2] Wang L, Trivedi D, Prezhdo O V 2014 J. Chem. Theory Comput. 10 3598
Google Scholar
[3] 郑镇法, 蒋翔, 褚维斌, 张丽丽, 郭宏礼, 赵传寓, 王亚南, 王傲雷, 郑奇靖, 赵瑾 2021 70 177101
Google Scholar
Zheng Z F, Jiang X, Chu W B, Zhang L L, Guo H L, Zhao C Y, Wang Y N, Wang A L, Zheng Q J, Zhao J 2021 Acta Phys. Sin. 70 177101
Google Scholar
[4] Sun X 2016 Chin. Phys. Lett. 33 123601
Google Scholar
[5] Sun X 2018 Commun. Theor. Phys. 69 308
Google Scholar
[6] Sun X 2021 Chem. Phys. 543 111089
Google Scholar
[7] Sun X 2022 Comput. Theor. Chem. 1212 113698
Google Scholar
[8] Scheit S, Goswami S, Meyer H, Köppel H 2019 Comput. Theor. Chem. 1150 71
Google Scholar
[9] 兰峥岗, 邵久书 2012 化学进展 24 1106
Lan Z G, Shao J S 2012 Prog. Chem. 24 1106
[10] An Z, Wu C Q, Sun X 2004 Phys. Rev. Lett. 93 216407
Google Scholar
[11] Wu C Q, Qiu Y, An Z, Nasu K 2003 Phys. Rev. B 68 125416
Google Scholar
[12] Sun Z, Li Y, Xie S J, An Z, Liu D S 2009 Phys. Rev. B 79 201310(R
Google Scholar
[13] Sun Z, Stafström S 2014 Phys. Rev. B 90 115420
Google Scholar
[14] Li Y, Gao K, Sun Z, Yin S, Liu D S, Xie S J 2008 Phys. Rev. B 78 014304
Google Scholar
[15] Gao K, Liu X J, Liu D S, Xie S J 2007 Phys. Rev. B 75 205412
Google Scholar
[16] Johansson Å, Stafström S 2000 Phys. Rev. Lett. 86 3602
Google Scholar
[17] Lima M P, Silva G M 2006 Phys. Rev. B 74 224304
Google Scholar
[18] Miranda R P, Fisher A J, Stella L, Horsfield A P 2011 J. Chem. Phys. 134 244102
Google Scholar
[19] Su W P, Schrieffer J, Heeger A J 1980 Phys. Rev. B 22 2099
Google Scholar
[20] 孙鑫, 吴大诚 1987 高聚物中的孤子和极化子(成都: 四川教育出版社)
Sun X, Wu D C 1987 Solitons and Polarons in Polymers (Chengdu: Sichuan Education Press
[21] Su W P, Schrieffer J R 1980 Proc. Natl. Acad. Sci. USA 77 5626
Google Scholar
[22] Ryabinkin I G, Nagesh J, Izmaylov A F 2015 J. Phys. Chem. Lett. 6 4200
Google Scholar
[23] 孙震, 安忠, 李元, 刘文, 刘德胜, 解士杰 2009 58 4150
Google Scholar
Sun Z, An Z, Li Y, Liu W, Liu D S, Xie S J 2009 Acta Phys. Sin. 58 4150
Google Scholar
-
图 1 电子从价带激发到导带示意图 (a) HOMO→LUMO; (b) HOMO–1→LUMO+1; (c) HOMO–2→LUMO+2
Fig. 1. The diagram of electronic excitation from valence band to conduction band: (a) HOMO→LUMO; (b) HOMO–1→LUMO+1; (c) HOMO–2→LUMO+2.
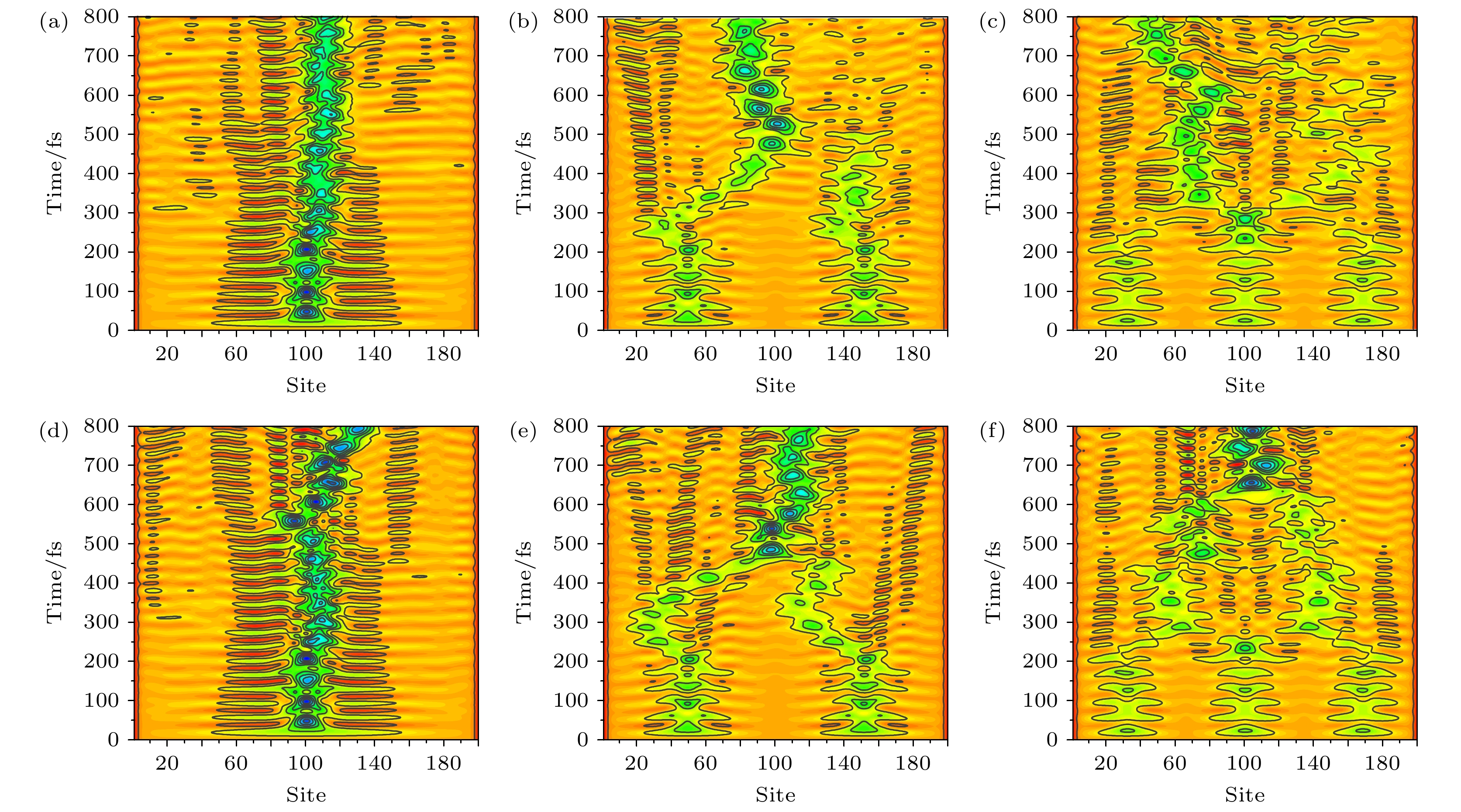
图 2 绝热表象(a)—(c)和透热表象(d)—(f)下晶格位形随时间的演化, 从左到右对应的光激发过程分别为HOMO→LUMO, HOMO–1→LUMO+1和HOMO–2→LUMO+2
Fig. 2. Lattice configuration evolution under adiabatic representation (a)–(c) and diabatic representation (d)–(f). From left to right, the photoexcitation dynamical processes are HOMO→LUMO, HOMO–1→LUMO+1 and HOMO–2→LUMO+2, respectively.
图 3 绝热表象下HOMO–1→LUMO+1光激发过程中导带中最低五条能级随时间的演化
Fig. 3. Time evolution of the lowest energy levels in conduction band under adiabatic representation, corresponding to the photoexcitation of HOMO–1→LUMO+1.
图 4 (a)—(c)分别对应LUMO, LUMO+1和LUMO+2的轨道波函数
Fig. 4. (a)–(c) Correspond to the wave functions of LUMO, LUMO+1 and LUMO+2, respectively.
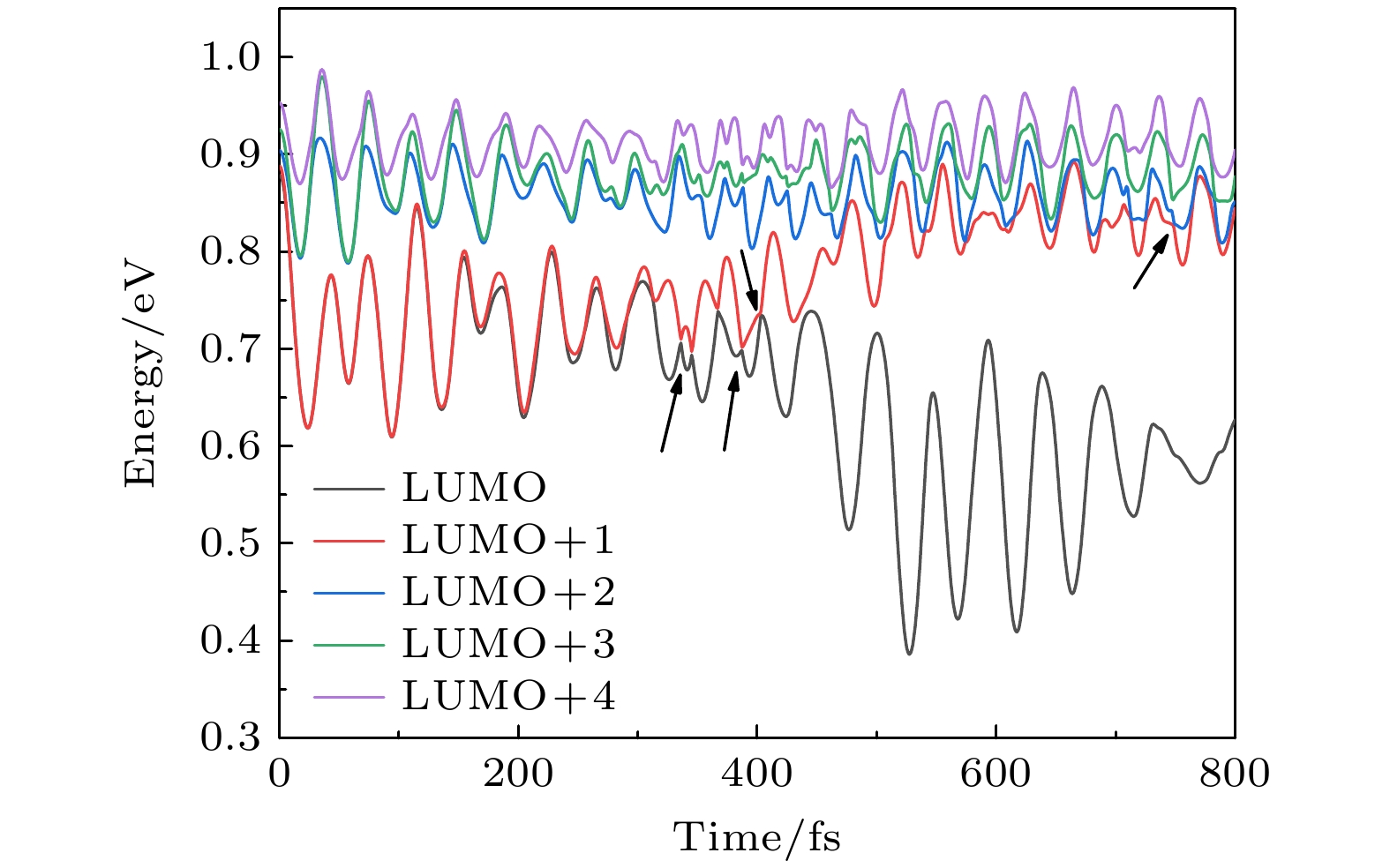
图 5 在光激发过程 (a) HOMO→LUMO, (b) HOMO-1→LUMO+1和(c) HOMO-2→LUMO+2中, 不同能级间的非绝热耦合强度随时间的演化, 其中黑线和红线分别代表数值和解析计算结果
Fig. 5. Time dependence of nonadiabatic coupling between different molecular orbitals in the photoexcitation processes: (a) HOMO→LUMO, (b) HOMO-1→LUMO+1 and (c) HOMO-2→LUMO+2, the black and red lines denote the numerical and analytic results, respectively.
-
[1] Stafström S 2010 Chem. Soc. Rev. 39 2484
Google Scholar
[2] Wang L, Trivedi D, Prezhdo O V 2014 J. Chem. Theory Comput. 10 3598
Google Scholar
[3] 郑镇法, 蒋翔, 褚维斌, 张丽丽, 郭宏礼, 赵传寓, 王亚南, 王傲雷, 郑奇靖, 赵瑾 2021 70 177101
Google Scholar
Zheng Z F, Jiang X, Chu W B, Zhang L L, Guo H L, Zhao C Y, Wang Y N, Wang A L, Zheng Q J, Zhao J 2021 Acta Phys. Sin. 70 177101
Google Scholar
[4] Sun X 2016 Chin. Phys. Lett. 33 123601
Google Scholar
[5] Sun X 2018 Commun. Theor. Phys. 69 308
Google Scholar
[6] Sun X 2021 Chem. Phys. 543 111089
Google Scholar
[7] Sun X 2022 Comput. Theor. Chem. 1212 113698
Google Scholar
[8] Scheit S, Goswami S, Meyer H, Köppel H 2019 Comput. Theor. Chem. 1150 71
Google Scholar
[9] 兰峥岗, 邵久书 2012 化学进展 24 1106
Lan Z G, Shao J S 2012 Prog. Chem. 24 1106
[10] An Z, Wu C Q, Sun X 2004 Phys. Rev. Lett. 93 216407
Google Scholar
[11] Wu C Q, Qiu Y, An Z, Nasu K 2003 Phys. Rev. B 68 125416
Google Scholar
[12] Sun Z, Li Y, Xie S J, An Z, Liu D S 2009 Phys. Rev. B 79 201310(R
Google Scholar
[13] Sun Z, Stafström S 2014 Phys. Rev. B 90 115420
Google Scholar
[14] Li Y, Gao K, Sun Z, Yin S, Liu D S, Xie S J 2008 Phys. Rev. B 78 014304
Google Scholar
[15] Gao K, Liu X J, Liu D S, Xie S J 2007 Phys. Rev. B 75 205412
Google Scholar
[16] Johansson Å, Stafström S 2000 Phys. Rev. Lett. 86 3602
Google Scholar
[17] Lima M P, Silva G M 2006 Phys. Rev. B 74 224304
Google Scholar
[18] Miranda R P, Fisher A J, Stella L, Horsfield A P 2011 J. Chem. Phys. 134 244102
Google Scholar
[19] Su W P, Schrieffer J, Heeger A J 1980 Phys. Rev. B 22 2099
Google Scholar
[20] 孙鑫, 吴大诚 1987 高聚物中的孤子和极化子(成都: 四川教育出版社)
Sun X, Wu D C 1987 Solitons and Polarons in Polymers (Chengdu: Sichuan Education Press
[21] Su W P, Schrieffer J R 1980 Proc. Natl. Acad. Sci. USA 77 5626
Google Scholar
[22] Ryabinkin I G, Nagesh J, Izmaylov A F 2015 J. Phys. Chem. Lett. 6 4200
Google Scholar
[23] 孙震, 安忠, 李元, 刘文, 刘德胜, 解士杰 2009 58 4150
Google Scholar
Sun Z, An Z, Li Y, Liu W, Liu D S, Xie S J 2009 Acta Phys. Sin. 58 4150
Google Scholar
下载:
计量
- 文章访问数: 1446
- PDF下载量: 60
- 被引次数: 0
