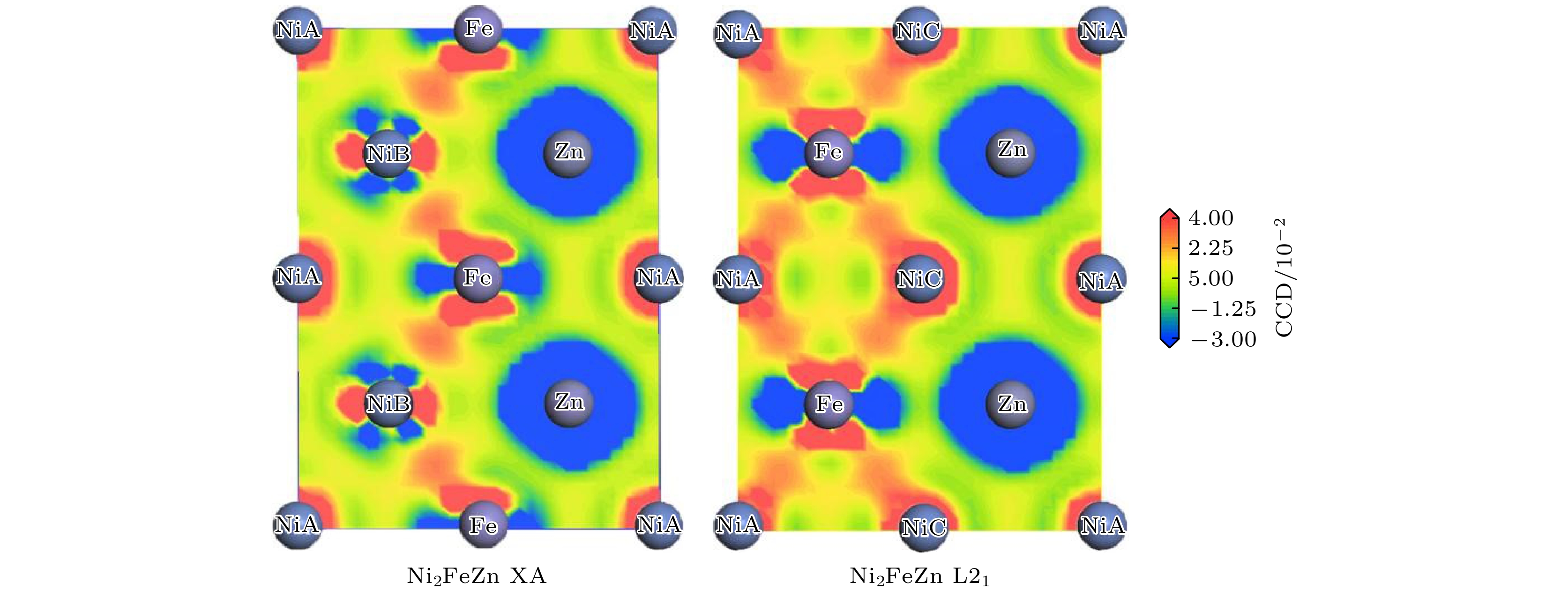
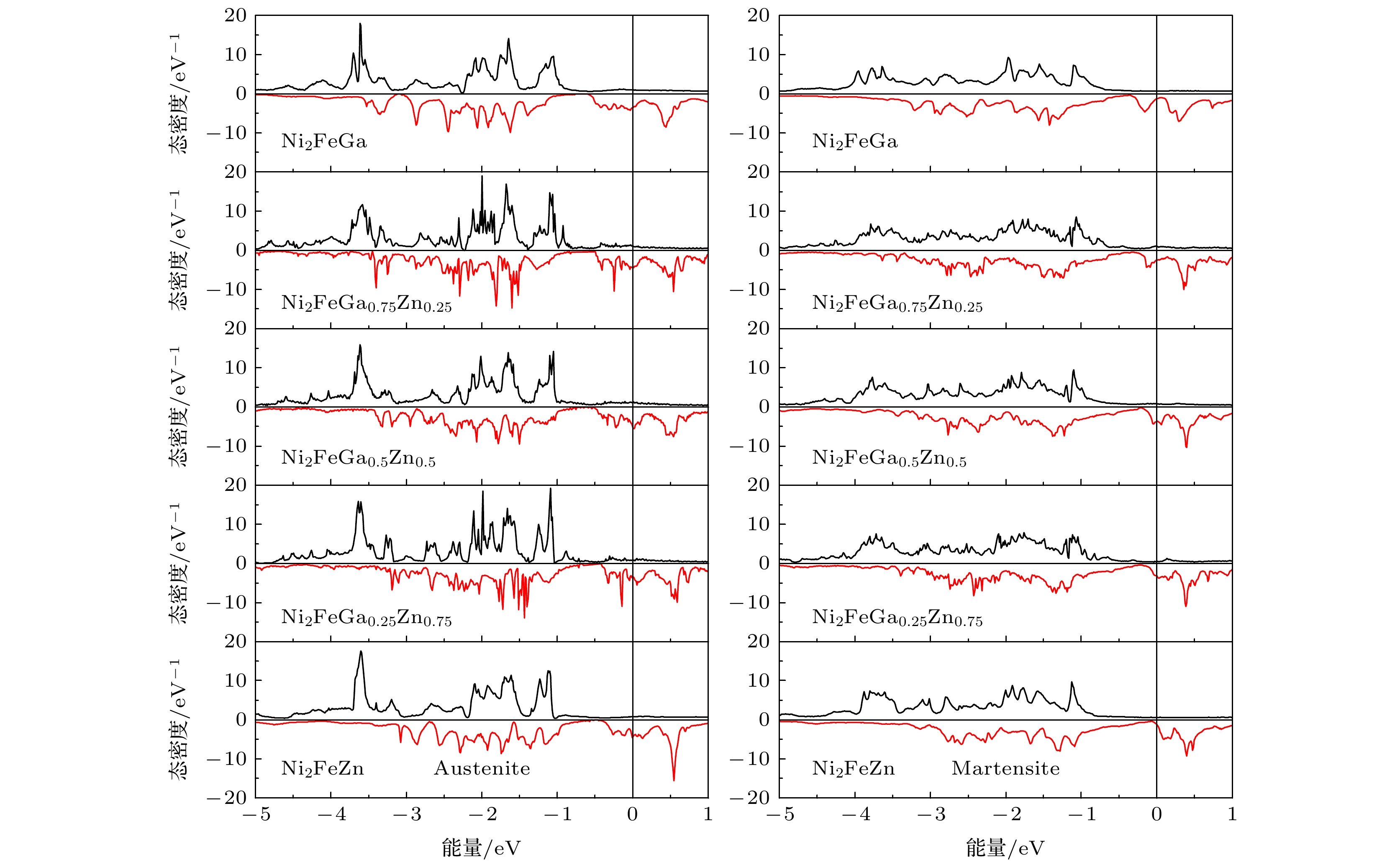
-
通过第一性原理计算研究了Zn掺杂对典型磁性形状记忆合金Ni2FeGa的电子结构、马氏体相变和磁性的影响. 在Ni2FeGa1–xZnx (x = 0, 0.25, 0.5, 0.75, 1)中, 取代Ga的Zn原子更倾向于占据Heusler合金晶格的D位. 计算表明Ni2FeGa1–xZnx合金马氏体和奥氏体相之间的能量差ΔEM随着Zn掺杂量的增加而不断增大, 这有助于增加Ni2FeGa1–xZnx马氏体相的稳定性并提高马氏体相变温度TM, 这一规律与材料态密度中的Jahn-Teller效应密切相关. 与此同时, Zn的掺杂没有改变这些合金的磁结构, Ni2FeGa1–xZnx合金中Ni, Fe原子磁矩始终为铁磁性耦合. 形成能Ef的计算表明, Zn掺杂会导致Ef略有增大, 但在整个研究的范围内形成能Ef始终保持为负值. 另外, Zn掺杂对Ni2FeGa的Heusler L21相有稳定作用, 有助于抑制面心结构L12相的产生.The magnetic shape memory alloys (MSMAs) have both martensitic transformation and ferromagnetism in the same material, thus external magnetic field can be used to induce/control the phase transformation or the reorientation of martensite variant. MSMAs have received considerable attention for their interesting properties and wide applications in different fields. For practical applications, the martensitic transformation temperature TM is an important factor and a high TM is preferable. Recently, Zn-doping has been found to be a possible way to elevate the value of TM of Ni-Mn based MSMA, but this effect on other kinds of MSMAs is not very clear yet. Heusler alloy Ni2FeGa is a typical MSMA with unique properties, however, its TM is relatively low. So it can be meaningful to find possible ways to increase its phase transition temperature. In this paper, the influences of Zn-doping on the electronic structure, martensitic transformation and magnetic properties of Heusler-type magnetic shape memory alloy Ni2FeGa are investigated by first-principle calculations. Total energy calculation and charge density difference indicate that Zn atom prefers to occupy the Ga (D) site when substituting for Ga in Ni2FeGa1–xZnx (x = 0, 0.25, 0.5, 0.75, 1). This main-group-element-like behavior is related to the closed 3d shell of Zn. Due to the similar atomic radii of Ga and Zn, Zn-doping does not lead the lattice constant to change greatly. The variation of the energy difference ΔEM between the martensite and austenite with Zn content increasing is calculated, and the result shows that ΔEM increases with Zn-doping increasing, and thus conducing to increasing the stability of the martensite phase and to evaluating the transformation temperature TM in Ni2FeGa1–xZnx. This trend can be explained by the Jahn-Teller effect observed in the DOS structure. The Zn-doping does not change the magnetic structure of Ni2FeGa. A ferromagnetic coupling between Fe spin moment and Ni spin moment can be observed within the whole range studied. The calculated total spin moment increases with Zn content increasing. The variation of formation energy Ef with Zn-doping is investigated. In Ni2FeGa1–xZnx a negative Ef is retained within the whole range studied, though it increases slightly with the doping of Zn. It is also found that the Zn-doping can increase the stability of L21 Heusler phase in Ni2FeGa1–xZnx and suppress the formation of the FCC L12 phase.
-
Keywords:
- Heusler alloys /
- magnetic shape memory alloys /
- electronic structure /
- martensitic transformation
[1] Dunand D C, Müllner P 2011 Adv. Mater. 23 216
Google Scholar
[2] Gottschall T, Skokov K P, Scheibel F, Acet M, Ghorbani Zavareh M, Skourski Y, Wosnitza J, Farle M, Gutfleisch O 2016 Phys. Rev. Appl. 5 024013
Google Scholar
[3] Ghosh S, Ghosh A, Mandal K 2018 J. Alloys Compd. 746 200
Google Scholar
[4] Ullakko K, Huang J K, Kanter C, Kokorin V V, O’Handley R C 1996 Appl. Phys. Lett. 69 1966
Google Scholar
[5] Liu Z H, Zhang M, Cui Y T, Zhou Y Q, Wang W H, Wu G H, Zhang X X 2003 Appl. Phys. Lett. 82 424
Google Scholar
[6] Karaca H E, Karaman I, Lagoudas D C, Maier H J, Chumlyakov Y I 2003 Scr. Mater. 49 831
Google Scholar
[7] Kainuma R, Imano Y, Ito W, Sutou Y, Morito H, Okamoto S, Kitakami O, Oikawa K, Fujita A, Kanomata T, Ishida K 2006 Nature 439 957
Google Scholar
[8] Omori T, Watanabe K, Umetsu R, Kainuma R, Ishida K 2009 Appl. Phys. Lett. 95 082508
Google Scholar
[9] Webster P J, Ziebeck K R A, Town S L, Peak M S 1984 Philos. Mag. B 49 295
Google Scholar
[10] Liu G D, Chen J L, Liu Z H, Dai X F, Wu G H, Zhang B, Zhang X X 2005 Appl. Phys. Lett. 87 262504
Google Scholar
[11] Han Z D, Wang D H, Zhang C L, Xuan H C, Zhang J R, Gu B X, Du Y W 2008 J. Appl. Phys. 104 053906
Google Scholar
[12] Algethami Obaidallah A, 李歌天, 柳祝红, 马星桥 2020 69 058102
Google Scholar
Algethami O A, Li T G, Liu Z H, Ma X Q 2020 Acta Phys. Sin. 69 058102
Google Scholar
[13] Zhang H H, Qian M F, Zhang X X, Wei L S, Cao F Y, Xing D W, Cui X P, Sun J F, Geng L 2016 J. Alloys Compd. 689 481
Google Scholar
[14] Luo H Z, Meng F B, Jiang Q X, Liu H Y, Liu E K, Wu G H, Wang Y X 2010 Scr. Mater. 63 569
Google Scholar
[15] Barton L S, Lazott R T, Marsten E R 2014 J. Appl. Phys. 115 17A908
Google Scholar
[16] Ni Z N, Guo X M, Li Q S, Liang Z Y, Luo H Z, Meng F B 2018 J. Magn. Magn. Mater. 464 65
Google Scholar
[17] Janovec J, Straka L, Sozinov A, Heczko O, Zelený M 2020 Mater. Res. Express 7 026101
[18] Ghotbi Varzaneh A, Kameli P, Abdolhosseini Sarsari I, Ghorbani Zavareh M, Salazar M C, Amiri T, Skourski Y, Luo J L, Etsell T H, Chernenko V A 2020 Phys. Rev. B 101 134403
Google Scholar
[19] Payne M C, Teter M P, Allan D C, Arias T A, Joannopoulos J D 1992 Rev. Mod. Phys. 64 1065
[20] Segall M D, Lindan P L D, Probert M J, Pickard C J, Hasnip P J, Clark S J, Payne M C 2002 J. Phys. Condens. Matter 14 2717
Google Scholar
[21] Vanderbilt D 1990 Phys. Rev. B 41 7892
Google Scholar
[22] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[23] Kandpal H C, Fecher G H, Felser C 2007 J. Phys. D: Appl. Phys. 40 1507
[24] Zhang R F, Veprek S, Argon A S 2008 Phys. Rev. B 77 172103
Google Scholar
[25] Gilleßen M, Dronskowski R 2010 J. Comput. Chem. 31 612
[26] Zhang Y J, Wang W H, Zhang H G, Liu E K, Ma R S, Wu G H 2013 Physica B 420 86
Google Scholar
[27] Cordero B, Gomez V, Platero-Prats A E, Reves M, Echeverría J, Cremades E, Barragan F, Alvarez S 2008 Dalton Trans. 21 2832
[28] 赵建涛, 赵昆, 王家佳, 余新泉, 于金, 吴三械 2012 61 213102
Google Scholar
Zhao J T, Zhao K, Wang J J, Yu X Q, Yu J, Wu S X 2012 Acta Phys. Sin. 61 213102
Google Scholar
[29] Wollmann L, Chadov S, Kübler J, Felser C 2011 Phys. Rev. B 92 064417
[30] Paul S, Ghosh S 2011 J. Appl. Phys. 110 063523
Google Scholar
[31] Luo H Z, Meng F B, Liu G D, Liu H Y, Jia P Z, Liu E K, Wang W H, Wu G H 2013 Intermetallics 38 139
Google Scholar
[32] Barman S R, Chakrabarti A, Singh S, Banik S, Bhardwaj S, Paulose P L, Chalke B A, Panda A K, Mitra A, Awasthi A M 2008 Phys. Rev. B 78 134406
Google Scholar
[33] Entel P, Dannenberg A, Siewert M, Herper H C, Gruner M E, Buchelnikov V D, Chernenko V A 2011 Mater. Sci. Forum 684 1
Google Scholar
[34] Winterlik J, Chadov S, Gupta A, Alijani V, Gasi T, Filsinger K, Balke B, Fecher G H, Jenkins C A, Casper F, Kubler J, Gao L, Parkin S S P, Felser C 2012 Adv. Mater. 24 6283
Google Scholar
[35] Faleev S V, Ferrante Y, Jeong J, Samant M G, Jones B, Parkin S S P 2017 Phys. Rev. Appl. 7 034022
Google Scholar
[36] Brown P J, Bargawi A Y, Crangle J, Neumann K U, Ziebeck K R A 1999 J. Phys. Condens. Matter 11 4715
Google Scholar
[37] Barman S R, Banik S, Shukla A K, Kamal C, Chakrabart A 2007 EPL 80 57002
Google Scholar
[38] Soykan C, Özdemir Kart S, Sevik C, Çağın T 2014 J. Alloys Compd. 611 225
Google Scholar
-
图 1 计算得到的Ni2FeGa1–xZnx (x = 0, 0.25, 0.5, 0.75, 1)合金总能量与晶格常数的关系曲线, 其中Zn(C)和Zn(D)分别表示Zn进入C和D晶位
Fig. 1. Calculated total energies of Ni2FeGa1–xZnx (x = 0, 0.25, 0.5, 0.75, 1) as functions of lattice constant. Here Zn (C) and Zn (D) indicate that Zn enters the C and D sites, respectively.
图 2 Ni2FeZn合金XA(左)和L21(右)结构在(110)面上的差分电荷密度
Fig. 2. The charge density difference on the (110) plane of Ni2FeZn alloy with XA (left) and L21 (right) structures.
图 3 Ni2FeGa1–xZnx中马氏体和奥氏体相能量差ΔEM随c/a比值的变化关系. 在图中, 零点对应于每种合金的立方奥氏体能量(c/a = 1)
Fig. 3. Variation of the energy difference ΔEM between the martensitic and austenitic phase with the c/a ratio in Ni2FeGa1–xZnx. Here the zero point corresponds to the cubic austenite (c/a = 1) of each alloy.
图 4 Ni2FeGa1–xZnx奥氏体和马氏体相总态密度的对比
Fig. 4. Comparison between the total DOS of austenitic and martensitic type Ni2FeGa1–xZnx.
图 5 Ni2FeGa, Ni2FeGa0.5Zn0.5和Ni2FeZn在L21和L12结构下的总能量与晶胞体积的函数关系. 图中ΔE表示L12和L21相之间的能量差
Fig. 5. The calculated total energies as functions of cell volume for Ni2FeGa, Ni2FeGa0.5Zn0.5 and Ni2FeZn with L21 and L12 structures. Here ΔE is the energy difference between the L12 and L21 phases.
图 6 L21和L12型Ni2FeGa1–xZnx (x = 0, 0.5, 1.0)的总态密度对比
Fig. 6. The total DOS of L21 and L12 type of Ni2FeGa1–xZnx (x = 0, 0.5, 1.0).
表 1 计算得到的Ni2FeGa1–xZnx(x = 0, 0.25, 0.5, 0.75, 1)合金立方奥氏体相的平衡晶格常数a, 形成能Ef和磁性参数
Table 1. The calculated equilibrium lattice constant a, formation energy Ef and magnetic properties of Ni2FeGa1–xZnx (x = 0, 0.25, 0.5, 0.75, 1) alloys in cubic austenitic state.
x 0.00 0.25 0.5 0.75 1.00 a/Å 5.76 5.76 5.75 5.74 5.74 Ef/(eV·f.u.–1) –0.75 –0.64 –0.54 –0.43 –0.34 Mt
(μB/f.u.)3.40 3.50 3.61 3.72 3.82 MNi/μB 0.16 0.20 0.25 0.30 0.35 MFe/μB 3.11 3.13 3.15 3.16 3.17 MGa/μB –0.03 –0.02 –0.01 0.00 — MZn/μB — –0.06 –0.06 –0.05 –0.04 
下载: 导出CSV
表 2 计算得到的Ni2FeGa1–xZnx (x = 0, 0.25, 0.5, 0.75, 1)合金在马氏体状态下的马氏体与奥氏体之间能量差ΔEM, c/a比值和磁性参数
Table 2. The calculated energy difference ΔEM between the martensite and austenite, c/a ratio and magnetic properties of Ni2FeGa1–xZnx (x = 0, 0.25, 0.5, 0.75, 1) alloys in tetragonal martensitic state.
x 0.00 0.25 0.5 0.75 1.00 ΔEM/(eV·f.u.–1) –0.110 –0.119 –0.128 –0.144 –0.151 c/a 1.36 1.36 1.34 1.33 1.32 Mt/(μB·f.u.–1) 3.38 3.48 3.63 3.73 3.85 MNi/μB 0.28 0.32 0.35 0.38 0.41 MFe/μB 2.92 3.00 3.02 3.06 3.11 MGa/μB –0.11 –0.10 –0.08 –0.07 — MZn/μB — –0.13 –0.11 –0.10 –0.09
下载: 导出CSV
-
[1] Dunand D C, Müllner P 2011 Adv. Mater. 23 216
Google Scholar
[2] Gottschall T, Skokov K P, Scheibel F, Acet M, Ghorbani Zavareh M, Skourski Y, Wosnitza J, Farle M, Gutfleisch O 2016 Phys. Rev. Appl. 5 024013
Google Scholar
[3] Ghosh S, Ghosh A, Mandal K 2018 J. Alloys Compd. 746 200
Google Scholar
[4] Ullakko K, Huang J K, Kanter C, Kokorin V V, O’Handley R C 1996 Appl. Phys. Lett. 69 1966
Google Scholar
[5] Liu Z H, Zhang M, Cui Y T, Zhou Y Q, Wang W H, Wu G H, Zhang X X 2003 Appl. Phys. Lett. 82 424
Google Scholar
[6] Karaca H E, Karaman I, Lagoudas D C, Maier H J, Chumlyakov Y I 2003 Scr. Mater. 49 831
Google Scholar
[7] Kainuma R, Imano Y, Ito W, Sutou Y, Morito H, Okamoto S, Kitakami O, Oikawa K, Fujita A, Kanomata T, Ishida K 2006 Nature 439 957
Google Scholar
[8] Omori T, Watanabe K, Umetsu R, Kainuma R, Ishida K 2009 Appl. Phys. Lett. 95 082508
Google Scholar
[9] Webster P J, Ziebeck K R A, Town S L, Peak M S 1984 Philos. Mag. B 49 295
Google Scholar
[10] Liu G D, Chen J L, Liu Z H, Dai X F, Wu G H, Zhang B, Zhang X X 2005 Appl. Phys. Lett. 87 262504
Google Scholar
[11] Han Z D, Wang D H, Zhang C L, Xuan H C, Zhang J R, Gu B X, Du Y W 2008 J. Appl. Phys. 104 053906
Google Scholar
[12] Algethami Obaidallah A, 李歌天, 柳祝红, 马星桥 2020 69 058102
Google Scholar
Algethami O A, Li T G, Liu Z H, Ma X Q 2020 Acta Phys. Sin. 69 058102
Google Scholar
[13] Zhang H H, Qian M F, Zhang X X, Wei L S, Cao F Y, Xing D W, Cui X P, Sun J F, Geng L 2016 J. Alloys Compd. 689 481
Google Scholar
[14] Luo H Z, Meng F B, Jiang Q X, Liu H Y, Liu E K, Wu G H, Wang Y X 2010 Scr. Mater. 63 569
Google Scholar
[15] Barton L S, Lazott R T, Marsten E R 2014 J. Appl. Phys. 115 17A908
Google Scholar
[16] Ni Z N, Guo X M, Li Q S, Liang Z Y, Luo H Z, Meng F B 2018 J. Magn. Magn. Mater. 464 65
Google Scholar
[17] Janovec J, Straka L, Sozinov A, Heczko O, Zelený M 2020 Mater. Res. Express 7 026101
[18] Ghotbi Varzaneh A, Kameli P, Abdolhosseini Sarsari I, Ghorbani Zavareh M, Salazar M C, Amiri T, Skourski Y, Luo J L, Etsell T H, Chernenko V A 2020 Phys. Rev. B 101 134403
Google Scholar
[19] Payne M C, Teter M P, Allan D C, Arias T A, Joannopoulos J D 1992 Rev. Mod. Phys. 64 1065
[20] Segall M D, Lindan P L D, Probert M J, Pickard C J, Hasnip P J, Clark S J, Payne M C 2002 J. Phys. Condens. Matter 14 2717
Google Scholar
[21] Vanderbilt D 1990 Phys. Rev. B 41 7892
Google Scholar
[22] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[23] Kandpal H C, Fecher G H, Felser C 2007 J. Phys. D: Appl. Phys. 40 1507
[24] Zhang R F, Veprek S, Argon A S 2008 Phys. Rev. B 77 172103
Google Scholar
[25] Gilleßen M, Dronskowski R 2010 J. Comput. Chem. 31 612
[26] Zhang Y J, Wang W H, Zhang H G, Liu E K, Ma R S, Wu G H 2013 Physica B 420 86
Google Scholar
[27] Cordero B, Gomez V, Platero-Prats A E, Reves M, Echeverría J, Cremades E, Barragan F, Alvarez S 2008 Dalton Trans. 21 2832
[28] 赵建涛, 赵昆, 王家佳, 余新泉, 于金, 吴三械 2012 61 213102
Google Scholar
Zhao J T, Zhao K, Wang J J, Yu X Q, Yu J, Wu S X 2012 Acta Phys. Sin. 61 213102
Google Scholar
[29] Wollmann L, Chadov S, Kübler J, Felser C 2011 Phys. Rev. B 92 064417
[30] Paul S, Ghosh S 2011 J. Appl. Phys. 110 063523
Google Scholar
[31] Luo H Z, Meng F B, Liu G D, Liu H Y, Jia P Z, Liu E K, Wang W H, Wu G H 2013 Intermetallics 38 139
Google Scholar
[32] Barman S R, Chakrabarti A, Singh S, Banik S, Bhardwaj S, Paulose P L, Chalke B A, Panda A K, Mitra A, Awasthi A M 2008 Phys. Rev. B 78 134406
Google Scholar
[33] Entel P, Dannenberg A, Siewert M, Herper H C, Gruner M E, Buchelnikov V D, Chernenko V A 2011 Mater. Sci. Forum 684 1
Google Scholar
[34] Winterlik J, Chadov S, Gupta A, Alijani V, Gasi T, Filsinger K, Balke B, Fecher G H, Jenkins C A, Casper F, Kubler J, Gao L, Parkin S S P, Felser C 2012 Adv. Mater. 24 6283
Google Scholar
[35] Faleev S V, Ferrante Y, Jeong J, Samant M G, Jones B, Parkin S S P 2017 Phys. Rev. Appl. 7 034022
Google Scholar
[36] Brown P J, Bargawi A Y, Crangle J, Neumann K U, Ziebeck K R A 1999 J. Phys. Condens. Matter 11 4715
Google Scholar
[37] Barman S R, Banik S, Shukla A K, Kamal C, Chakrabart A 2007 EPL 80 57002
Google Scholar
[38] Soykan C, Özdemir Kart S, Sevik C, Çağın T 2014 J. Alloys Compd. 611 225
Google Scholar
下载:
计量
- 文章访问数: 4427
- PDF下载量: 77
- 被引次数: 0
