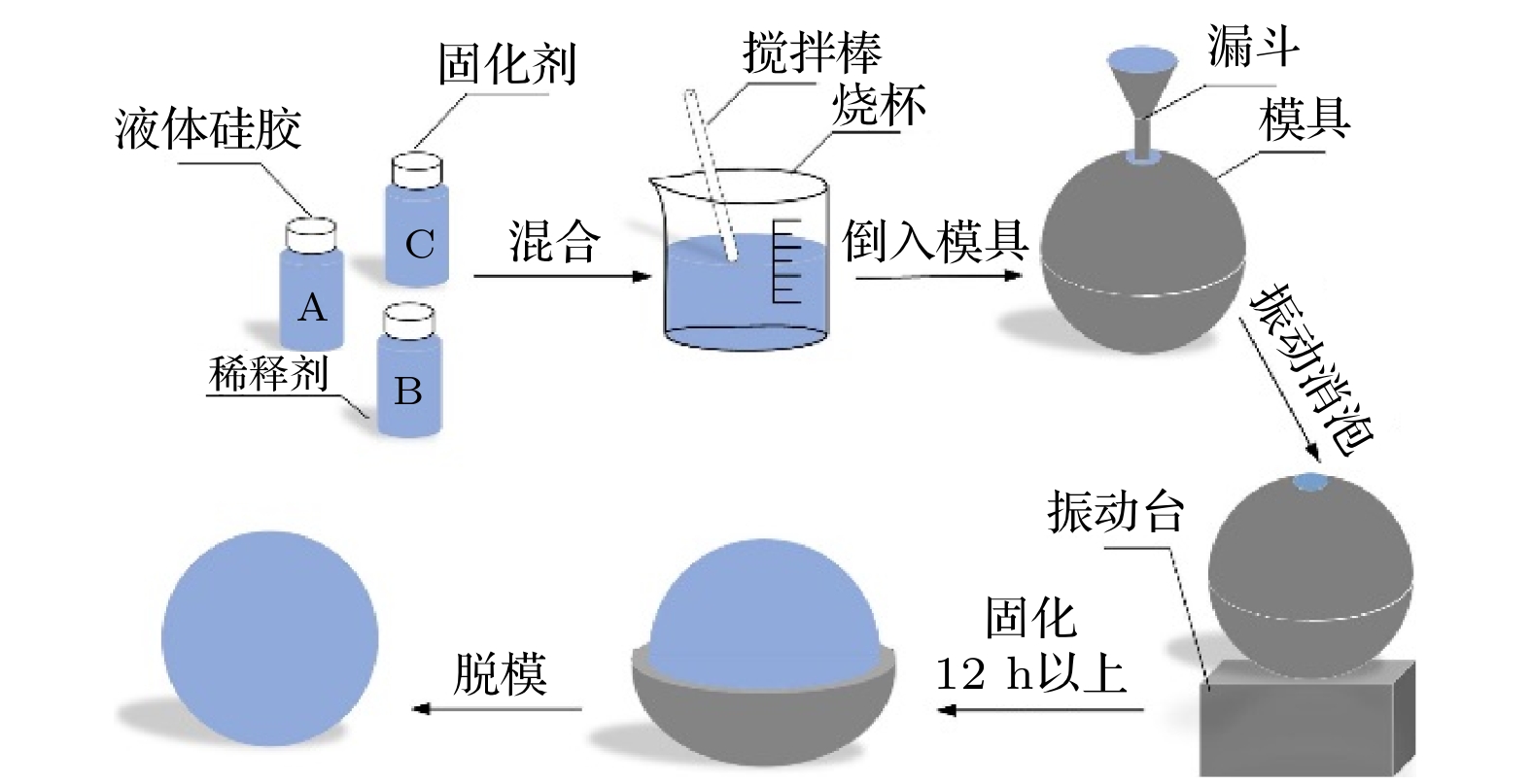
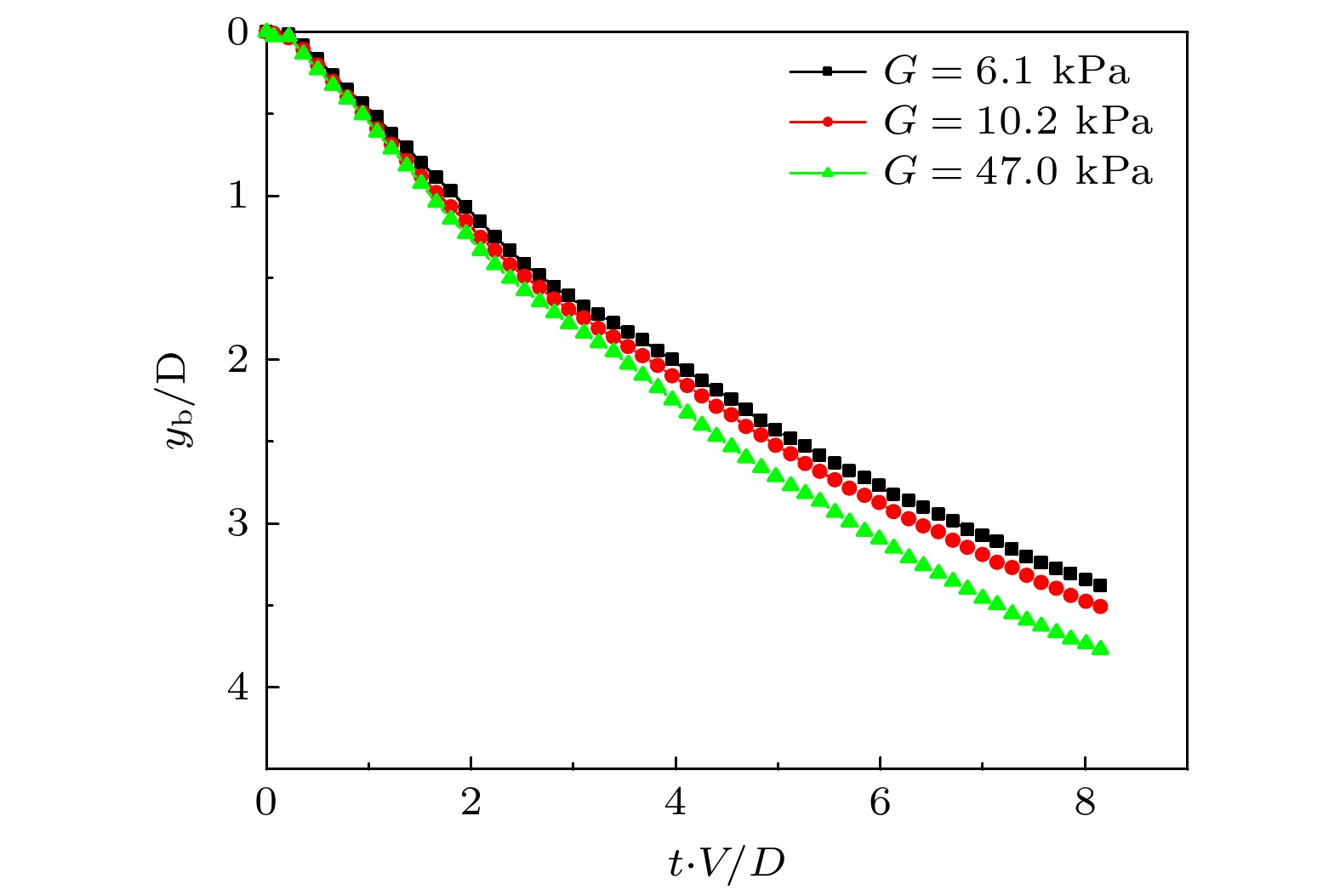
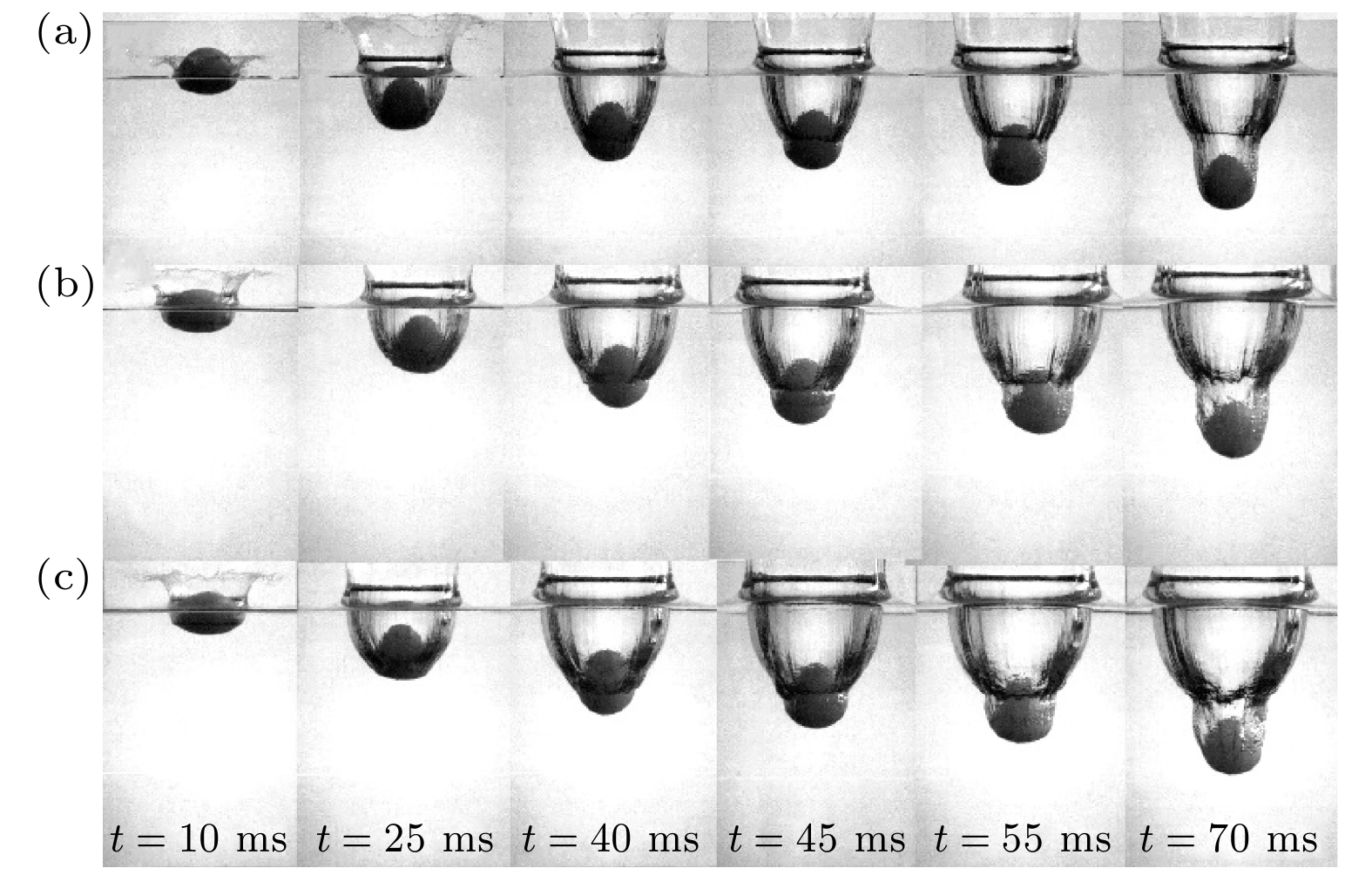
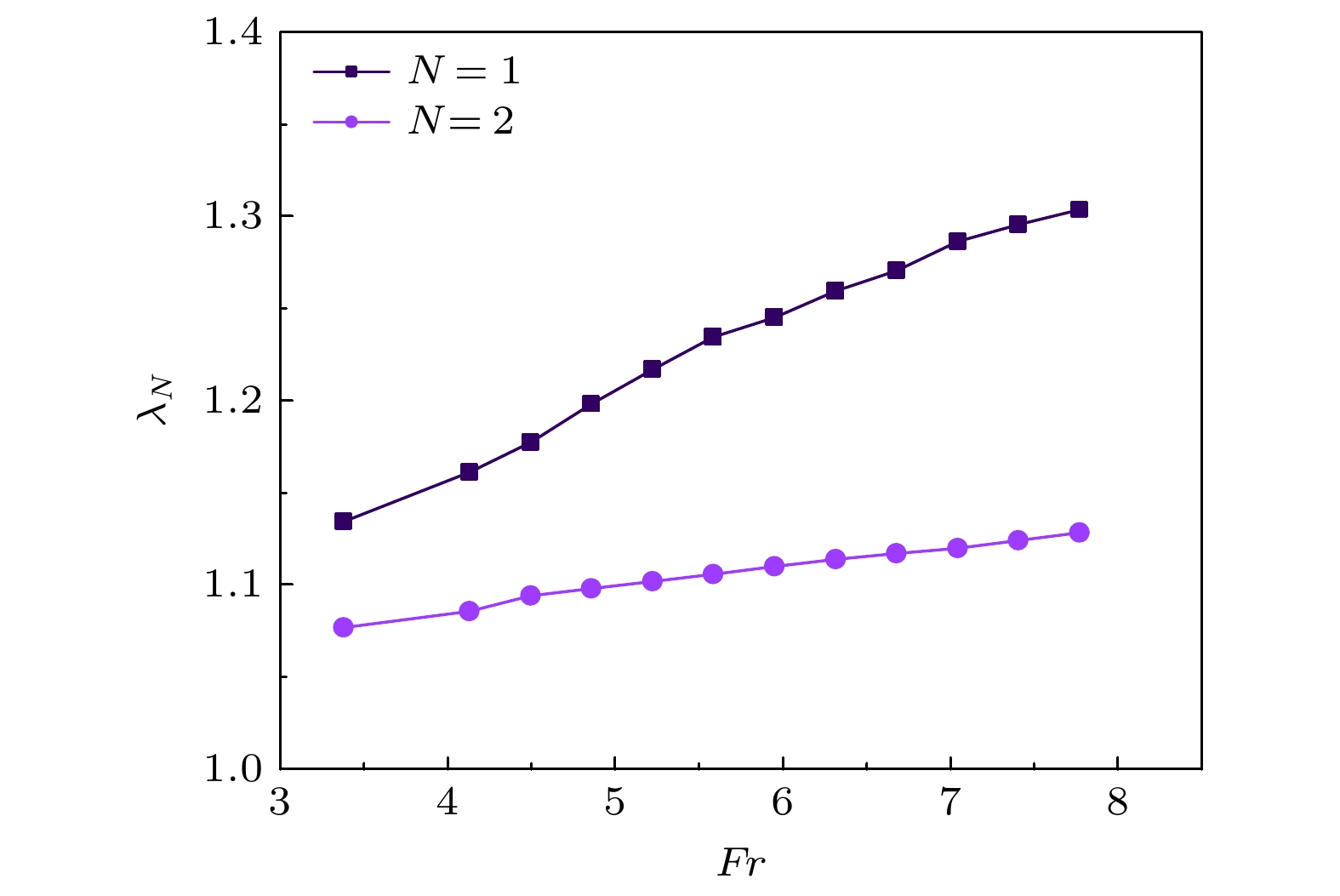
-
超弹性材料是工程实际中常用的材料, 具有很强的非线性力学性能. 将超弹性材料应用于入水问题是一个新的跨学科研究方向. 与传统的刚性球体入水现象不同, 超弹性球体入水后极易发生变形. 为了探究该大变形的入水流固耦合问题, 本文采用高速摄像方法, 对超弹性球体垂直入水问题开展实验研究. 基于实验结果, 对比分析了球体材料属性和入水冲击条件对入水空泡流动及球体变形行为的影响. 实验结果表明, 超弹性球体入水后产生嵌套空泡现象的条件是需要足够大的入水冲击条件和小的材料剪切模量. 嵌套空泡产生和保持的时间与球体的剪切模量和直径有关. 超弹性球体的入水位移及其形成空泡的长度随入水冲击速度和剪切模量的增大而增大, 却随球体直径的增大而减小. 入水冲击速度的增加只会加剧球体的变形程度, 而不影响嵌套空泡的产生时刻. 同时, 本文对球体的变形行为随弗劳德数和剪切模量与水动力之比的变化特性进行了描述与研究.Hyperelastic materials, which have strong nonlinear mechanical properties, are commonly used in the engineering field. The application of hyperelastic materials to the water entry problem is a new interdisciplinary research topic. Unlike the water entering into a traditional rigid sphere, the hyperelastic sphere is very easy to deform during water entry. In order to explore the fluid-structure coupling problem with large deformations during water entry, a high-speed camera is used to study the problem of vertical water entering into hyperelastic sphere in this paper. Based on the experimental results, the effects of the material properties and impacting conditions on the cavity flow and sphere deformation behaviors during water entry are compared and analyzed. The experimental results show that the formation of the nested cavity after impacting a free surface of the hyperelastic sphere needs large enough impact conditions and small material shear modulus. The time for the nested cavity to be formed and retained during water entry is related to the material shear modulus and sphere diameter. The sphere displacement and length of cavity formed by the hyperelastic sphere increase with the increase of the impact velocity and material shear modulus, but decrease with the increase of the diameter of the sphere. The increase of the impacting velocity can only aggravate the deformation behaviors of the hyperelastic sphere, but does not affect the formation moment of the nested cavity. In addition, the characteristics for the deformation behaviors of the hyperelastic sphere to vary with the Froude number and the dimensionless ratio of material shear modulus to impacting hydrodynamic pressure are described and studied.
-
Keywords:
- hyperelastic spheres /
- water entry /
- nested cavity /
- deformation
[1] Kubota Y, Mochizuki O 2015 WJM 5 129
Google Scholar
[2] Epps B P, Techet A H 2007 Exp. Fluids. 43 691
Google Scholar
[3] Sun T, Wang H, Zou L, Zong Z, Li H 2019 Ocean. Eng. 194 106597
Google Scholar
[4] Xia W, Cong W, Wei Y, Li C 2020 Appl. Ocean. Res. 103 102322
Google Scholar
[5] Xia W X, Wang C, Wei Y J, Li J C, Yang L 2020 Exp. Fluids. 61 57
Google Scholar
[6] Worthington A M, Cole R S 1897 Philos. Trans. R. Soc. London 189 137
Google Scholar
[7] Worthington A M 1881 P. Roy. Soc. A. Math Phy. 33 347
[8] Wood R W 1909 Science 29 464
Google Scholar
[9] Duclaux V, Caillé F, Duez C, Ybert C, Bocquet L, Clanet C 2007 J. Fluid Mech. 591 1
Google Scholar
[10] Seddon C M, Moatamedi M 2006 Int. J. Impact. Eng. 32 1045
Google Scholar
[11] May A 1952 J. Appl. Phys. 23 1362
Google Scholar
[12] Yang L, Wei Y, Wang C, Xia W, Li J 2020 J. Appl. Phys. 127 064901
Google Scholar
[13] Truscott T T, Epps B P, Techet A H 2012 J. Fluid Mech. 704 173
Google Scholar
[14] Aristoff J M, Truscott T T, Techet A H, Bush J W M 2010 Phys. Fluids 22 70
[15] Aristoff J M, Bush J W M 2009 J. Fluid Mech. 619 45
Google Scholar
[16] 何春涛, 王聪, 何乾坤, 仇洋 2012 61 134701
Google Scholar
He C T, Wang C, He Q K, Qiu Y 2012 Acta Phys. Sin. 61 134701
Google Scholar
[17] 施红辉, 周浩磊, 吴岩, 贾会霞, 张晓萍, 周素云, 章利特, 董若凌 2012 力学学报 44 49
Google Scholar
Shi H H, Zhou H L, Wu Y, Jia H X, Zhang X P, Zhou S Y, Zhang L T, Dong R L 2012 J. Mech. Phys. Solids. 44 49
Google Scholar
[18] 李佳川, 魏英杰, 王聪, 邓环宇 2016 65 204703
Google Scholar
Li J C, Wei Y J, Wang C, Deng H Y 2016 Acta Phys. Sin. 65 204703
Google Scholar
[19] 李佳川, 魏英杰, 王聪 2019 兵工学报 40 124
Google Scholar
Li J C, Wei Y J, Wang C 2019 Acta. Armamentarii. 40 124
Google Scholar
[20] 卢佳兴, 魏英杰, 王聪, 路丽睿, 许昊 2019 力学学报 51 150
Lu J X, Wei Y J, Wang C, Lu L R, Xu H 2019 J. Mech. Phys. Solids. 51 150
[21] Yun H, Lyu X, Wei Z 2020 Ocean. Eng. 201 107143
Google Scholar
[22] Yun H, Lyu X, Wei Z 2020 J. Visual. Japan. 23 49
Google Scholar
[23] Truscott T T, Epps B P, Belden J 2014 Annu. Rev. Fluid Mech. 46 355
Google Scholar
[24] Truscott T T, Techet A H 2006 Phys. Fluids 18 4173
[25] Speirs N B, Mansoor M M, Belden J, Truscott T T 2019 J. Fluid Mech. 862 R3
Google Scholar
[26] Russo S, Biscarini C, Facci A L, Falcucci G, Jannelli E 2017 J. Mar Sci Tech. Japan. 23 67
[27] Facci A L, Falcucci G, Agresta A, Biscarini C 2019 Water 11 1048
Google Scholar
[28] Russo S, Falcucci G 2018 ICNAAM. Greece 1987 25
[29] Panciroli R, Falcucci G, Erme G, Santis E D, Jannelli E 2015 Aip. Conference, AIP Publishing LLC, April 1, 1648 570011
[30] 孙士丽 2011 博士学位论文 (哈尔滨: 哈尔滨工程大学)
Sun S L 2011 Ph. D. Dissertation (Harbin: Harbin Engineering University) (in Chinese)
[31] Hurd R C, Belden J, Jandron M A, Fanning D T, Bower A F, Truscott T T 2017 J. Fluid Mech. 824 912
Google Scholar
-
图 5 不同剪切模量球体入水空泡形态对比 (a) G = 6.1 kPa; (b) G = 10.2 kPa; (c) G = 47.0 kPa
Fig. 5. Comparison of cavity shapes formed by hyperelastic spheres with different shear moduli: (a) G = 6.1 kPa; (b) G = 10.2 kPa; (c) G = 47.0 kPa.
图 7 不同冲击速度下球体入水空泡形态对比 (a)V = 1.1 m/s; (b) V = 2.5 m/s; (c) V = 3.3 m/s
Fig. 7. Comparison of cavity shapes formed by hyperelastic spheres with different impact velocities: (a)V = 1.1 m/s; (b) V = 2.5 m/s; (c) V = 3.3 m/s.
图 9 不同冲击速度下嵌套空泡形态对比 (a) V = 3.3 m/s; (b) V = 4.4 m/s; (c) V = 4.8 m/s
Fig. 9. Comparison of nested cavities with different impact velocities: (a) V = 3.3 m/s; (b) V = 4.4 m/s; (c) V = 4.8 m/s.
图 10 不同直径球体入水空泡形态对比 (a) D = 80 mm; (b) D = 61 mm; (c) D = 56 mm
Fig. 10. Comparison of cavity shapes formed by hyperelastic spheres with different diameters: (a) D = 80 mm; (b) D = 61 mm; (c) D = 56 mm.
图 12 超弹性球体入水变形量系数的时间历程
Fig. 12. Time history of sphere deformation coefficient during water entry.
图 13 超弹性球体(G = 10.2 kPa)第一、二变形周期内λN随Fr的变化
Fig. 13. Change of λN in the first and second deformation cycles (G = 10.2 kPa) with Fr
图 14 超弹性球体(D = 61 mm)第一、二变形周期内λN随η的变化
Fig. 14. Change of λN in the first and second deformation cycles (D = 61 mm) with η.
-
[1] Kubota Y, Mochizuki O 2015 WJM 5 129
Google Scholar
[2] Epps B P, Techet A H 2007 Exp. Fluids. 43 691
Google Scholar
[3] Sun T, Wang H, Zou L, Zong Z, Li H 2019 Ocean. Eng. 194 106597
Google Scholar
[4] Xia W, Cong W, Wei Y, Li C 2020 Appl. Ocean. Res. 103 102322
Google Scholar
[5] Xia W X, Wang C, Wei Y J, Li J C, Yang L 2020 Exp. Fluids. 61 57
Google Scholar
[6] Worthington A M, Cole R S 1897 Philos. Trans. R. Soc. London 189 137
Google Scholar
[7] Worthington A M 1881 P. Roy. Soc. A. Math Phy. 33 347
[8] Wood R W 1909 Science 29 464
Google Scholar
[9] Duclaux V, Caillé F, Duez C, Ybert C, Bocquet L, Clanet C 2007 J. Fluid Mech. 591 1
Google Scholar
[10] Seddon C M, Moatamedi M 2006 Int. J. Impact. Eng. 32 1045
Google Scholar
[11] May A 1952 J. Appl. Phys. 23 1362
Google Scholar
[12] Yang L, Wei Y, Wang C, Xia W, Li J 2020 J. Appl. Phys. 127 064901
Google Scholar
[13] Truscott T T, Epps B P, Techet A H 2012 J. Fluid Mech. 704 173
Google Scholar
[14] Aristoff J M, Truscott T T, Techet A H, Bush J W M 2010 Phys. Fluids 22 70
[15] Aristoff J M, Bush J W M 2009 J. Fluid Mech. 619 45
Google Scholar
[16] 何春涛, 王聪, 何乾坤, 仇洋 2012 61 134701
Google Scholar
He C T, Wang C, He Q K, Qiu Y 2012 Acta Phys. Sin. 61 134701
Google Scholar
[17] 施红辉, 周浩磊, 吴岩, 贾会霞, 张晓萍, 周素云, 章利特, 董若凌 2012 力学学报 44 49
Google Scholar
Shi H H, Zhou H L, Wu Y, Jia H X, Zhang X P, Zhou S Y, Zhang L T, Dong R L 2012 J. Mech. Phys. Solids. 44 49
Google Scholar
[18] 李佳川, 魏英杰, 王聪, 邓环宇 2016 65 204703
Google Scholar
Li J C, Wei Y J, Wang C, Deng H Y 2016 Acta Phys. Sin. 65 204703
Google Scholar
[19] 李佳川, 魏英杰, 王聪 2019 兵工学报 40 124
Google Scholar
Li J C, Wei Y J, Wang C 2019 Acta. Armamentarii. 40 124
Google Scholar
[20] 卢佳兴, 魏英杰, 王聪, 路丽睿, 许昊 2019 力学学报 51 150
Lu J X, Wei Y J, Wang C, Lu L R, Xu H 2019 J. Mech. Phys. Solids. 51 150
[21] Yun H, Lyu X, Wei Z 2020 Ocean. Eng. 201 107143
Google Scholar
[22] Yun H, Lyu X, Wei Z 2020 J. Visual. Japan. 23 49
Google Scholar
[23] Truscott T T, Epps B P, Belden J 2014 Annu. Rev. Fluid Mech. 46 355
Google Scholar
[24] Truscott T T, Techet A H 2006 Phys. Fluids 18 4173
[25] Speirs N B, Mansoor M M, Belden J, Truscott T T 2019 J. Fluid Mech. 862 R3
Google Scholar
[26] Russo S, Biscarini C, Facci A L, Falcucci G, Jannelli E 2017 J. Mar Sci Tech. Japan. 23 67
[27] Facci A L, Falcucci G, Agresta A, Biscarini C 2019 Water 11 1048
Google Scholar
[28] Russo S, Falcucci G 2018 ICNAAM. Greece 1987 25
[29] Panciroli R, Falcucci G, Erme G, Santis E D, Jannelli E 2015 Aip. Conference, AIP Publishing LLC, April 1, 1648 570011
[30] 孙士丽 2011 博士学位论文 (哈尔滨: 哈尔滨工程大学)
Sun S L 2011 Ph. D. Dissertation (Harbin: Harbin Engineering University) (in Chinese)
[31] Hurd R C, Belden J, Jandron M A, Fanning D T, Bower A F, Truscott T T 2017 J. Fluid Mech. 824 912
Google Scholar
下载:
计量
- 文章访问数: 6240
- PDF下载量: 119
- 被引次数: 0
