-
设计了一种非周期排布的低雷达散射截面超表面天线阵列. 该阵列由两种天线单元构成, 两种天线单元的上层贴片形状相同, 正交放置, 作为天线单元能以同种极化方式在相同频带下工作, 作为超表面单元相互之间能形成180° ± 37°的有效相位差. 阵列在x极化方向与y极化方向上分别利用相位对消与吸波原理减缩雷达散射截面. 同时, 根据编码超材料理论, 使用编程软件将两种单元进行非周期编码, 使阵列的反射场呈漫散射状分布, 有效降低了其峰值雷达散射截面. 仿真结果显示天线阵列的辐射性能良好. 与同等大小的金属板相比, 在x极化波垂直入射时, 设计天线阵列单站雷达散射截面(radar cross section, RCS)的6 dB减缩带宽为4.8—7.4 GHz, 相对带宽为42.6%; 在y极化波垂直入射时, 设计天线阵列单站RCS的6 dB减缩带宽为4.6—7.8 GHz, 相对带宽为51.6%. 同时, 设计天线阵较棋盘式天线阵散射能量分布更加均匀, 空间中RCS峰值明显降低. 实测结果与仿真结果符合较好.An aperiodic metasurface antenna array with low radar cross section (RCS) is designed. The upper patches of the two antenna elements have the same shape and are placed at an orthogonal position, which can effectively reduce the workload of simulating the reflection characteristics of the patch. As antenna elements, they have identical operational band and polarization mode, and as metasurfaces, they can form an effective phase difference of 180° ± 37°. The RCS of the array is reduced mainly by phase cancellation under the x polarization and by absorption under the y polarization. According to the coding metamaterial theory, the two elements can be coded aperiodically by using the programming software. Regarding element A and element B as “0” and “1”, respectively, the coding matrix can be solved by a genetic algorithm. Element A and element B are arranged according to positions “0” and “1” to obtain a proposed array. The scattering field of proposed array is diffusive, and the peak RCS is effectively reduced. In order to highlight the characteristics of the proposed array, the chessboard-type array is designed for comparison. The simulation results show that the radiation performance of proposed array is good. Comparing with the metal board of the same size, the 6 dB reduction bandwidth of the monostatic RCS is 4.8－7.4 GHz (relative bandwidth is 42.6%) under the x polarization and 4.6－7.8 GHz (relative bandwidth is 51.6%) under the y polarization. Comparing with the chessboard type array, the scattering energy distribution of the designed antenna array is very uniform and the peak RCS in space reduces obviously. When a 4.8 GHz electromagnetic wave is incident with different incident angles and polarization modes, the scattering field is diffusive. Compared with other similar arrays, the proposed array has advantages of simple design process and even scattering field. The experimental results are in good agreement with the simulation results. This work makes full use of the scattering characteristics of the antenna element itself to solve the problem that the array antenna possesses both good radiation characteristics and low scattering characteristics at the same time, and improves the design process of the antenna patch. This design method has certain universality and reference significance for designing the low RCS antenna array.
-
Keywords:
- low radar cross section /
- patch antenna array /
- diffusion
[1] 李文强, 曹祥玉, 高军, 赵一, 杨欢欢, 刘涛 2015 64 094102
Google Scholar
Li W Q, Cao X Y, Gao J, Zhao Y, Yang H H, Liu T 2015 Acta Phys. Sin. 64 094102
Google Scholar
[2] Son X T, Ikmo P 2014 IEEE Antennas Wirel. Propag. Lett. 13 587
Google Scholar
[3] Li G H, Zhai H Q, Li L, Liang C H, Yu R D, Liu S 2015 IEEE Trans. Antennas Propag. 63 525
Google Scholar
[4] Yoon J H, Yoon Y J, Lee W, So J 2012 Electron. Lett. 48 50
Google Scholar
[5] Deng T W, Li Z W, Chen Z N 2017 IEEE Trans. Antennas Propag. 65 5886
Google Scholar
[6] Saptarshi G, Kumar V S 2018 IEEE Trans. Electromagn. Compat. 60 166
Google Scholar
[7] Yan M B, Qu S B, Wang J F, Zhang J Q, Zhang A X, Xia S, Wang W J 2014 IEEE Antennas Wirel. Propag. Lett. 13 639
Google Scholar
[8] Bai Y, Zhao L, Ju D Q 2015 Opt. Express 23 8670
Google Scholar
[9] Agarwal M, Behera A K, Meshram M K 2016 Electron. Lett. 52 340
Google Scholar
[10] Ren J Y, Gong S X, Jiang W 2018 IEEE Antennas Wirel. Propag. Lett. 17 102
Google Scholar
[11] Liu X B, Zhang J S, Li W, Lu R, Zhu S T, Xu Z, Zhang A X 2017 IEEE Antennas Wirel. Propag. Lett. 16 1028
Google Scholar
[12] Zhang L B, Zhou P H, Lu H P, Zhang L 2016 Opt. Mater. 6 1393
Google Scholar
[13] 于惠存, 曹祥玉, 高军, 杨欢欢, 韩江枫, 朱学文, 李桐 2018 67 224101
Google Scholar
Yu H C, Cao X Y, Gao J, Yang H H, Han J F, Zhu X W, Li T 2018 Acta Phys. Sin. 67 224101
Google Scholar
[14] Zhang J M, Yan L, Li L P, Zhang T, Li H H, Wang Q M, Hao Y N, Lei M, Bi K 2017 J. Appl. Phys. 122 014501
Google Scholar
[15] Li Y F, Zhang J Q, Qu S B, Wang J F, Chen H Y, Xu Z, Zhang A X 2014 Appl. Phys. Lett. 104 221110
Google Scholar
[16] Wang X P, Wan L L, Chen T N, Song A L, Du X W 2016 AIP Adv. 6 065320
Google Scholar
[17] Sharma A, Gangwar D, Kanaujia B K, Dwari S 2018 AEU Int. J. Electron. Commun. 91 132
Google Scholar
[18] Liu X, Gao J, Cao X Y, Zhao Y, Li S J 2017 IEEE Antennas Wirel. Propag. Lett. 16 724
Google Scholar
[19] Su J X, Kong C Y, Li Z R, Yin H C, Yang Y Q 2017 Electron. Lett. 53 1088
Google Scholar
[20] Zheng Y J, Cao X Y, Gao J, Yang H H, Zhou Y L, Liu T 2017 Opt. Express 25 30001
Google Scholar
[21] 兰俊祥, 曹祥玉, 高军, 韩江枫, 刘涛, 丛丽丽, 王思铭 2019 68 034101
Google Scholar
Lan J X, Cao X Y, Gao J, Han J F, Liu T, Cong L L, Wang S M 2019 Acta Phys. Sin. 68 034101
Google Scholar
[22] Liu Y, Jia Y T, Zhang W B, Wang Y Z, Gong S X, Liao G S 2019 IEEE Trans. Antennas Propag. 67 6199
Google Scholar
-
图 1 天线单元结构示意图 (a) 单元A立体结构; (b) 单元B立体结构; (c) 单元A平面结构; (d) 单元B平面结构
Fig. 1. Three-dimensional geometry of (a) element A and (b) B; two-dimensional geometry of (c) element A and (d) B.
图 2 不同参数对两单元性能的影响 (a) l2对单元A反射相位的影响; (b) l2对单元A反射幅度的影响; (c) l2对两单元|S11|的影响; (d) l6对单元A反射相位的影响; (e) l6对单元A反射幅度的影响; (f) l6对两单元|S11|的影响
Fig. 2. Effects of l2 and l6: Effects of l2 on (a) reflection phase of element A, (b) reflection magnitude of element A, and (c) |S11| of element A and B; effects of l6 on (d) reflection phase of element A, (e) reflection magnitude of element A, and (f) |S11| of element A and B.
图 3 不同参数对单元B性能的影响 (a) lp2对反射相位的影响; (b) lp2对反射幅度的影响; (c) lp2对|S11|的影响; (d) ls对反射相位的影响; (e) ls对反射幅度的影响; (f) ls对|S11|的影响
Fig. 3. Effects of lp2 and ls on element B: Effects of lp2 on (a) reflection phase, (b) reflection magnitude, and (c) |S11|; effects of ls on (d) reflection phase, (e) reflection magnitude, and (f) |S11|.
图 4 两单元的辐射特性 (a) |S11|及增益曲线; (b) 单元A在5 GHz时的辐射方向图; (c) 单元B在5 GHz时的辐射方向图
Fig. 4. Radiation characteristics of two elements: (a) |S11| and gain; radiation pattern of (b) element A and (c) element B at 5 GHz.
图 5 两单元的反射特性 (a) 反射相位; (b) 反射相位差; (c) 反射幅度
Fig. 5. Reflection characteristics of two elements: (a) Reflection phase; (b) reflection phase difference; (c) reflection magnitude.
图 6 两单元表面电流分布 (a) 单元A在5.7 GHz时; (b)单元B在4.7 GHz时
Fig. 6. Surface current distributions of (a) element A at 5.7 GHz and (b) element B at 4.7 GHz.
图 7 天线阵列结构示意图 (a) 设计天线阵; (b) 棋盘式天线阵
Fig. 7. Geometry of (a) proposed array and (b) chessboard type array.
图 8 两天线阵列辐射特性 (a) 实际增益曲线; (b) 设计天线阵中心单元的|S11|曲线; (c) 设计天线阵在5 GHz时的辐射方向图; (d) 棋盘式天线阵在5 GHz时的辐射方向图
Fig. 8. Radiation characteristics of two arrays: (a) Realized gain; (b) |S11| of elements of proposed array; radiation pattern of (c) proposed array and (d) chessboard type array at 5 GHz.
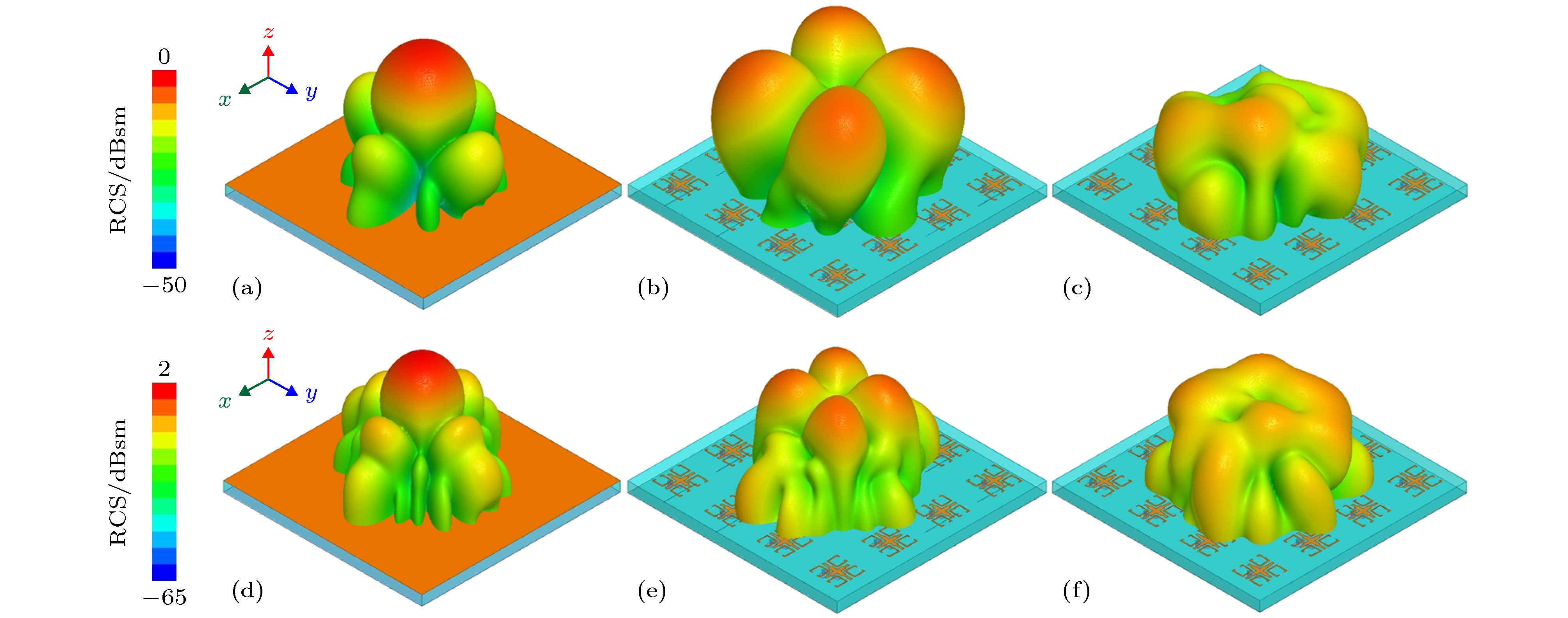
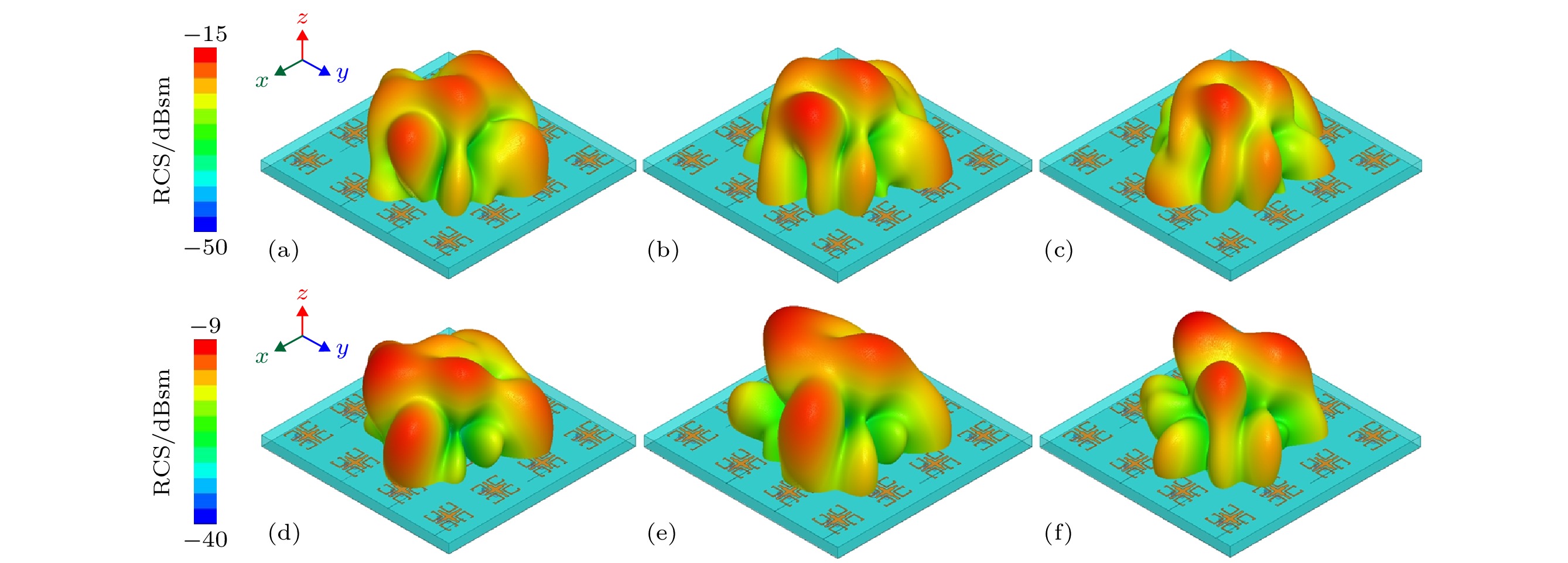
图 10 垂直入射时三维散射场分布 (a) 5 GHz时金属板散射场分布; (b) 5 GHz时棋盘式天线阵散射场分布; (c) 5 GHz时设计天线阵散射场分布; (d) 6.4 GHz时金属板散射场分布; (e) 6.4 GHz时棋盘式天线阵散射场分布; (f) 6.4 GHz时设计天线阵散射场分布
Fig. 10. Three-dimensional scattering field for normal incidence: (a) Metal board, (b) chessboard type array and (c) proposed array at 5 GHz; (d) metal board, (e) chessboard type array and (f) proposed array at 6.4 GHz.
图 11 斜入射时三维散射场分布 (a) TE极化波15°入射; (b) TE极化波30°入射; (c) TE极化波45°入射; (d) TM极化波15°入射; (e) TM极化波30°入射; (f) TM极化波45°入射
Fig. 11. Three-dimensional scattering field: (a) 15°, (b) 30°, (c) 45° under TE polarized plane wave; (d) 15°, (e) 30°, (f) 45° under TM polarized plane wave.
图 12 天线阵镜像双站RCS减缩曲线 (a) TM极化波; (b) TE极化波
Fig. 12. Mirror bistatic RCS reduction: (a) TM polarized plane wave; (b) TE polarized plane wave.
图 13 样品天线测试 (a) 天线阵样品; (b) 功分器; (c) 散射测试环境
Fig. 13. Testing proposed array: (a) Sample; (b) power dividers; (c) testing environment of scattering performance.
图 14 实测天线阵中心单元的|S11|曲线 (a) E1单元; (b) E2单元; (c) E3单元; (d) E4单元
Fig. 14. Measured |S11| of elements of proposed array: (a) E1; (b) E2; (c) E3; (d) E4.
图 15 实测天线阵方向图 (a) xoz面; (b) yoz面
Fig. 15. Measured radiation patterns of proposed array: (a) xoz plane; (b) yoz plane.
图 16 实测天线阵单站RCS减缩曲线 (a) x极化; (b) y极化
Fig. 16. Measured monostatic RCS reduction: (a) x-polarized; (b) y-polarized.
-
[1] 李文强, 曹祥玉, 高军, 赵一, 杨欢欢, 刘涛 2015 64 094102
Google Scholar
Li W Q, Cao X Y, Gao J, Zhao Y, Yang H H, Liu T 2015 Acta Phys. Sin. 64 094102
Google Scholar
[2] Son X T, Ikmo P 2014 IEEE Antennas Wirel. Propag. Lett. 13 587
Google Scholar
[3] Li G H, Zhai H Q, Li L, Liang C H, Yu R D, Liu S 2015 IEEE Trans. Antennas Propag. 63 525
Google Scholar
[4] Yoon J H, Yoon Y J, Lee W, So J 2012 Electron. Lett. 48 50
Google Scholar
[5] Deng T W, Li Z W, Chen Z N 2017 IEEE Trans. Antennas Propag. 65 5886
Google Scholar
[6] Saptarshi G, Kumar V S 2018 IEEE Trans. Electromagn. Compat. 60 166
Google Scholar
[7] Yan M B, Qu S B, Wang J F, Zhang J Q, Zhang A X, Xia S, Wang W J 2014 IEEE Antennas Wirel. Propag. Lett. 13 639
Google Scholar
[8] Bai Y, Zhao L, Ju D Q 2015 Opt. Express 23 8670
Google Scholar
[9] Agarwal M, Behera A K, Meshram M K 2016 Electron. Lett. 52 340
Google Scholar
[10] Ren J Y, Gong S X, Jiang W 2018 IEEE Antennas Wirel. Propag. Lett. 17 102
Google Scholar
[11] Liu X B, Zhang J S, Li W, Lu R, Zhu S T, Xu Z, Zhang A X 2017 IEEE Antennas Wirel. Propag. Lett. 16 1028
Google Scholar
[12] Zhang L B, Zhou P H, Lu H P, Zhang L 2016 Opt. Mater. 6 1393
Google Scholar
[13] 于惠存, 曹祥玉, 高军, 杨欢欢, 韩江枫, 朱学文, 李桐 2018 67 224101
Google Scholar
Yu H C, Cao X Y, Gao J, Yang H H, Han J F, Zhu X W, Li T 2018 Acta Phys. Sin. 67 224101
Google Scholar
[14] Zhang J M, Yan L, Li L P, Zhang T, Li H H, Wang Q M, Hao Y N, Lei M, Bi K 2017 J. Appl. Phys. 122 014501
Google Scholar
[15] Li Y F, Zhang J Q, Qu S B, Wang J F, Chen H Y, Xu Z, Zhang A X 2014 Appl. Phys. Lett. 104 221110
Google Scholar
[16] Wang X P, Wan L L, Chen T N, Song A L, Du X W 2016 AIP Adv. 6 065320
Google Scholar
[17] Sharma A, Gangwar D, Kanaujia B K, Dwari S 2018 AEU Int. J. Electron. Commun. 91 132
Google Scholar
[18] Liu X, Gao J, Cao X Y, Zhao Y, Li S J 2017 IEEE Antennas Wirel. Propag. Lett. 16 724
Google Scholar
[19] Su J X, Kong C Y, Li Z R, Yin H C, Yang Y Q 2017 Electron. Lett. 53 1088
Google Scholar
[20] Zheng Y J, Cao X Y, Gao J, Yang H H, Zhou Y L, Liu T 2017 Opt. Express 25 30001
Google Scholar
[21] 兰俊祥, 曹祥玉, 高军, 韩江枫, 刘涛, 丛丽丽, 王思铭 2019 68 034101
Google Scholar
Lan J X, Cao X Y, Gao J, Han J F, Liu T, Cong L L, Wang S M 2019 Acta Phys. Sin. 68 034101
Google Scholar
[22] Liu Y, Jia Y T, Zhang W B, Wang Y Z, Gong S X, Liao G S 2019 IEEE Trans. Antennas Propag. 67 6199
Google Scholar
下载:
计量
- 文章访问数: 7979
- PDF下载量: 216
- 被引次数: 0
