转角石墨烯体系的拓扑特性和轨道磁性

刘健鹏; 戴希

doi:10.7498/aps.69.20200506

摘要

本文介绍了转角双层石墨烯和多层石墨烯中的电子结构、拓扑性质以及轨道磁性. 在转角双层石墨烯中, 由于两层石墨烯之间的相对旋转会形成具有长周期的摩尔条纹. 由转角产生的摩尔势场会在摩尔超元胞中产生方向相反的赝磁场, 与两层的石墨烯中的狄拉克电子耦合, 从而产生赝朗道能级. 而魔角石墨烯中的每个谷和自旋自由度的两条平带就等价于两个具有相反陈数的零赝朗道能级. 这样的赝朗道能级表示可以很自然地解释一系列“魔角”的来源, 也对理解魔角双层石墨烯中观测到的关联绝缘态和量子反常霍尔效应具有重要意义. 本文进一步讨论了转角多层石墨烯, 并发现转角多层石墨烯体系中普遍存在具有非平庸拓扑性质的平带. 这些拓扑平带通常具有非零的谷陈数, 并且在一定近似下可以由一个普适的规律描述. 本文还讨论了转角石墨烯体系中的拓扑平带所具有的轨道磁性. 如果时间反演对称性自发破缺, 转角石墨烯体系会处于一个谷极化的基态. 这样的谷极化基态是一个在摩尔尺度上的轨道磁性态, 在摩尔超胞中具有纳米尺度的环状电流分布. 之前的理论提出在转角双层石墨烯体系中观测到的关联绝缘态的本质就是一种净磁矩为零的“摩尔轨道反铁磁态”. 当体系的$C_{2z}$对称性被氮化硼衬底破坏时, 转角石墨烯中的谷极化基态则变成了一种“摩尔轨道铁磁态”, 它不仅具有(量子)反常霍尔效应, 也具有新奇的磁光效应和非线性光学响应.

关键词:

Abstract

We review and discuss the electronic structures, topological properties and orbital magnetism in twisted bilayer (TBG) and multilayer graphene systems. Moiré pattern is formed in twisted bilayer graphene due to the mutual twist of the two graphene layers. The moiré potential induced by the twist can generate opposite pseudo magnetic fields in the Moiré supercell, which are coupled with the Dirac fermions and generate two sets of pseudo Landau levels with opposite Chern numbers $\pm1$. The two flat bands for each valley each spin of TBG are equivalent to the two zeroth pseudo Landau levels with opposite Chern numbers and opposite sublattice polarizations. Such a pseudo-Landau-level representation has significant implications on the quantum anomalous Hall states observed at integer fillings of the flat bands in TBG at the magic angle. The origin of the magic angle can also be naturally explained by using the pseudo-Landau-level picture. We further discuss twisted multilayer graphene systems, and show that topological flat bands generally exist in the twisted multilayer graphene systems. These topological flat bands have nonzero valley Chern numbers, which can be described by a succinct formula under certain approxmations. These topological flat bands in twisted bilayer and multilayer graphene systems are associated with orbital magnetism. A valley polarized state in the twist graphene system is an orbital magnetic state with nontrivial current-loop pattern in the moiré supercell. The experimentally observed correlated insulating states at $\pm 1/2$ fillings and at charge neutrality point of magic-angle TBG can be valley polarized states, which are associated with compensating current loops and induce staggered orbital magnetizations on the moiré length scale. If $C_{2z}$ symmetry is broken due to the alignment of hexagonal boron nitride substrate, then a valley-polarized ground state would be a moiré orbital ferromagnetic state, which exhibits not only (quantum) anomalous Hall effect, but also novel magneto-optical and nonlinear optical responses.

Keywords:

作者及机构信息

刘健鹏^1,2,
戴希²

1.
上海科技大学物质科学与技术学院, 上海　201210

2.
香港科技大学物理系, 香港

通信作者: 刘健鹏, liujp@shanghaitech.edu.cn ; 戴希, daix@ust.hk

基金项目: 香港研究资助局 (批准号: GRF16300918) 资助的课题

Authors and contacts

Liu Jian-Peng^1,2,
Dai Xi²

1.
School of Physical Science and Technology, Shanghai Tech University, Shanghai 201210, China

2.
Department of Physics, Hong Kong University of Science and Technology, Hong Kong, China

Corresponding author: Liu Jian-Peng, liujp@shanghaitech.edu.cn ; Dai Xi, daix@ust.hk

Funds: Project supported by the Hong Kong Research Grants Council Project, China (Grant No. GRF16300918

文章全文

参考文献

[1]	Lopes dos Santos J M B, Peres N M R, Castro Neto A H 2007 Phys. Rev. Lett. 99 256802 Google Scholar
[2]	Mele E J 2010 Phys. Rev. B 81 161405 Google Scholar
[3]	Trambly de Laissardiere G, Mayou D, Magaud L 2010 Nano Lett. 10 804 Google Scholar
[4]	Bistritzer R, MacDonald A H 2011 Proc. Natl. Acad. Sci. 108 12233 Google Scholar
[5]	Lopes dos Santos J M B, Peres N M R, Castro Neto A H 2012 Phys. Rev. B 86 155449 Google Scholar
[6]	San-Jose P, González J, Guinea F 2012 Phys. Rev. Lett. 108 216802 Google Scholar
[7]	Cao Y, Fatemi V, Demir A, et al. 2018 Nature 556 80 Google Scholar
[8]	Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E, Jarillo-Herrero P 2018 Nature 556 43 Google Scholar
[9]	Yankowitz M, Chen S, Polshyn H, Zhang Y, Watanabe K, Taniguchi T, Graf D, Young A F, Dean C R 2019 Science 363 1059 Google Scholar
[10]	Sharpe A L, Fox E J, Barnard A W, Finney J, Watanabe K, Taniguchi T, Kastner M A, Goldhaber-Gordon D 2019 Science 365 605 Google Scholar
[11]	Serlin M, Tschirhart C, Polshyn H, Zhang Y, Zhu J, Watanabe K, Taniguchi T, Balents L, Young A 2019 Science 367 900
[12]	Stepanov P, Das I, Lu X, Fahimniya A, Watanabe K, Taniguchi T, Koppens F H, Lischner J, Levitov L, Efetov D K 2019 arXiv preprint arXiv: 1911.09198
[13]	Po H C, Zou L, Vishwanath A, Senthil T 2018 Phys. Rev. X 8 031089
[14]	Koshino M, Yuan N F Q, Koretsune T, Ochi M, Kuroki K, Fu L 2018 Phys. Rev. X 8 031087
[15]	Kang J, Vafek O 2018 Phys. Rev. X 8 031088
[16]	Isobe H, Yuan N F Q, Fu L 2018 Phys. Rev. X 8 041041
[17]	Xu X Y, Law K T, Lee P A 2018 Phys. Rev. B 98 121406 Google Scholar
[18]	Huang T, Zhang L, Ma T 2019 Sci. Bull. 64 310 Google Scholar
[19]	Liu C C, Zhang L D, Chen W Q, Yang F 2018 Phys. Rev. Lett. 121 217001 Google Scholar
[20]	Rademaker L, Mellado P 2018 Phys. Rev. B 98 235158 Google Scholar
[21]	Venderbos J W F, Fernandes R M 2018 Phys. Rev. B 98 245103 Google Scholar
[22]	Kang J, Vafek O 2019 Phys. Rev. Lett. 122 246401 Google Scholar
[23]	Xie M, MacDonald A H 2020 Phys. Rev. Lett. 124 097601 Google Scholar
[24]	Jian C M, Xu C 2018 arXiv preprint arXiv: 1810.03610
[25]	Bultinck N, Chatterjee S, Zaletel M P 2020 Phys. Rev. Lett. 124 166601 Google Scholar
[26]	Zhang Y H, Mao D, Senthil T 2019 Phys. Rev. Res. 1 033126 Google Scholar
[27]	Liu S, Khalaf E, Lee J Y, Vishwanath A 2019 arXiv preprint arXiv: 1905.07409
[28]	Wu F, Das Sarma S 2020 Phys. Rev. Lett. 124 046403 Google Scholar
[29]	Chatterjee S, Bultinck N, Zaletel M P 2020 Phys. Rev. B 101 165141 Google Scholar
[30]	Alavirad Y, Sau J D 2019 arXiv preprint arXiv: 1907.13633
[31]	Cécile R, Dong Z H, Zhang Y H, Senthil T 2020 Phys. Rev. Lett. 124 187601 Google Scholar
[32]	Bultinck N, Khalaf E, Liu S, Chatterjee S, Vishwanath A, Zaletel M P 2019 arXiv preprent, arXiv: 1911.02045
[33]	Angeli M, Tosatti E, Fabrizio M 2019 Phys. Rev. X 9 041010
[34]	Zhang Y, Jiang K, Wang Z, Zhang F 2020 arXiv preprint arXiv: 2001.02476
[35]	Lu C, Zhang Y, Zhang Y, Zhang M, Liu C C, Gu Z C, Chen W Q, Yang F 2020 arXiv preprint arXiv: 2003.09513
[36]	Po H C, Zou L, Senthil T, Vishwanath A 2019 Phys. Rev. B 99 195455 Google Scholar
[37]	Song Z, Wang Z, Shi W, Li G, Fang C, Bernevig B A 2019 Phys. Rev. Lett. 123 036401 Google Scholar
[38]	Yuan N F Q, Fu L 2018 Phys. Rev. B 98 045103 Google Scholar
[39]	Zou L, Po H C, Vishwanath A, Senthil T 2018 Phys. Rev. B 98 085435 Google Scholar
[40]	Liu J, Dai X 2019 arXiv preprint arXiv: 1911.03760
[41]	Shen C, Chu Y, Wu Q, Li N, Wang S, Zhao Y, Tang J, Liu J, Tian J, Watanabe K, Taniguchi T, Yang R, Meng Z Y, Shi D, Yazyev O V, Zhang G 2020 Nat. Phys. 16 520 Google Scholar
[42]	Liu X, Hao Z, Khalaf E, Lee J Y, Watanabe K, Taniguchi T, Vishwanath A, Kim P 2019 arXiv preprint arXiv: 1903.08130
[43]	Cao Y, Rodan-Legrain D, Rubies-Bigorda O, Park J M, Watanabe K, Taniguchi T, Jarillo-Herrero P 2020 Nature 583 215 Google Scholar
[44]	Chen G, Sharpe A L, Fox E J, et al. 2020 Nature 579 56 Google Scholar
[45]	Chen G, Sharpe A L, Gallagher P, Rosen I T, Fox E J, Jiang L, Lyu B, Li H, Watanabe K, Taniguchi T, Jung J, Shi Z, GoldhaberGordon D, Zhang Y, Wang F 2019 Nature 572 215 Google Scholar
[46]	Chen G, Jiang L, Wu S, et al. 2019 Nat. Phys. 15 237 Google Scholar
[47]	Zhang Y H, Mao D, Cao Y, Jarillo-Herrero P, Senthil T 2019 Phys. Rev. B 99 075127 Google Scholar
[48]	Liu J, Ma Z, Gao J, Dai X 2019 Phys. Rev. X 9 031021
[49]	Lee J Y, Khalaf E, Liu S, Liu X, Hao Z, Kim P, Vishwanath A 2019 Nat. Commun. 10 5333 Google Scholar
[50]	Chebrolu N R, Chittari B L, Jung J 2019 Phys. Rev. B 99 235417 Google Scholar
[51]	Cea T, Walet N R, Guinea F 2019 Nano Lett. 19 8683 Google Scholar
[52]	Koshino M 2019 Phys. Rev. B 99 235406 Google Scholar
[53]	Ma Z, Li S, Zheng Y W, Xiao M M, Jiang H, Gao J H, Xie X 2019 arXiv preprint arXiv: 1905.00622
[54]	Haddadi F, Wu Q, Kruchkov A J, Yazyev O V 2020 Nano Lett. 20 2410 Google Scholar
[55]	Li S Y, Zhang Y, Ren Y N, Liu J, Dai X, He L 2019 arXiv preprint arXiv: 1912.13133
[56]	Liu J, Dai X 2020 npj Comput. Mater. 6 57 Google Scholar
[57]	de Gail R, Goerbig M O, Guinea F, Montambaux G, Castro Neto A H 2011 Phys. Rev. B 84 045436 Google Scholar
[58]	Uchida K, Furuya S, Iwata J I, Oshiyama A 2014 Phys. Rev. B 90 155451 Google Scholar
[59]	Liu J, Liu J, Dai X 2019 Phys. Rev. B 99 155415 Google Scholar
[60]	Jung J, Raoux A, Qiao Z, MacDonald A H 2014 Phys. Rev. B 89 205414 Google Scholar
[61]	Moon P, Koshino M 2014 Phys. Rev. B 90 155406 Google Scholar
[62]	Zhang Y H, Mao D, Senthil T 2019 arXiv preprint arXiv: 1901.08209
[63]	Ahn J, Park S, Yang B J 2019 Phys. Rev. X 9 021013
[64]	Yu R, Qi X L, Bernevig A, Fang Z, Dai X 2011 Phys. Rev. B 84 075119 Google Scholar
[65]	Soluyanov A A, Vanderbilt D 2011 Phys. Rev. B 83 235401 Google Scholar
[66]	Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802 Google Scholar
[67]	Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 226801 Google Scholar
[68]	Fu L, Kane C L 2007 Phys. Rev. B 76 045302 Google Scholar
[69]	Castro Neto A H, Guinea F, Peres N M R, Novoselov K S, Geim A K 2009 Rev. Mod. Phys. 81 109 Google Scholar
[70]	Zhang Y H, Senthil T 2019 Phys. Rev. B 99 205150 Google Scholar
[71]	Chittari B L, Chen G, Zhang Y, Wang F, Jung J 2019 Phys. Rev. Lett. 122 016401 Google Scholar
[72]	McCann E, Koshino M 2013 Rep. Prog. Phys. 76 056503 Google Scholar
[73]	Thonhauser T, Ceresoli D, Vanderbilt D, Resta R 2005 Phys. Rev. Lett. 95 137205 Google Scholar
[74]	Ceresoli D, Thonhauser T, Vanderbilt D, Resta R 2006 Phys. Rev. B 74 024408 Google Scholar
[75]	Shi J, Vignale G, Xiao D, Niu Q 2007 Phys. Rev. Lett. 99 197202 Google Scholar
[76]	Choi Y, Kemmer J, Peng Y, et al. 2019 Nat. Phys. 15 1174 Google Scholar
[77]	Jiang Y, Lai X, Watanabe K, Taniguchi T, Haule K, Mao J, Andrei E Y 2019 Nature 573 91 Google Scholar
[78]	Nagaosa N, Sinova J, Onoda S, MacDonald A, Ong N 2010 Rev. Mod. Phys. 82 1539 Google Scholar
[79]	Fukumura T, Toyosaki H, Ueno K, Nakano M, Yamasaki T, Kawasaki M 2007 Jpn. J. Appl. Phys. 46 L642 Google Scholar
[80]	Sarma S D, Pinczuk A 2008 Perspectives in Quantum Hall Effects: Novel Quantum Liquids in Low-dimensional Semiconductor Structures (Hoboken: John Wiley & Sons)
[81]	Wu F, Lovorn T, Tutuc E, Martin I, MacDonald A H 2019 Phys. Rev. Lett. 122 086402 Google Scholar
[82]	Wu F, Lovorn T, Tutuc E, MacDonald A H 2018 Phys. Rev. Lett. 121 026402 Google Scholar
[83]	Wang L, Shih E M, Ghiotto A, et al. 2019 arXiv preprint arXiv: 1910.12147
[84]	Regan E C, Wang D, Jin C, et al. 2020 Nature 579 359 Google Scholar
[85]	An L, Cai X, Huang M, Wu Z, Lin J, Ying Z, Ye Z, Feng X, Wang N 2019 arXiv preprint arXiv: 1907.03966
[86]	Zhang Y, Yuan N F, Fu L 2019 arXiv preprint arXiv: 1910.14061
[87]	Lian B, Liu Z, Zhang Y, Wang J 2020 Phys. Rev. Lett. 124 126402 Google Scholar
[88]	Hejazi K, Luo Z X, Balents L 2020 Proc. Natl. Acad. Sci. 117 10721 Google Scholar

施引文献

图 1 (a)转角双层石墨烯的摩尔条纹示意图, 插图展示两层石墨烯在不同区域层间距离的褶皱起伏; (b) 转角双层-双层石墨烯体系的示意图; (c)转角石墨烯体系的摩尔布里渊区示意图

Fig. 1. (a) Schematic illustration of the moiré pattern in twisted bilayer graphene, the inserted shows the wrinkles of the graphene for different layer distances; (b) schematic illustration of twisted double bilayer graphene system; (c) moiré Brillouin zone of twisted graphene systems.

下载: 全尺寸图片幻灯片

图 2 (a)转角双层石墨烯在魔角时的能带; (b)转角双层石墨烯中K谷两条平带的威尔逊圈 (以$2{\text{π}}$为单位)

Fig. 2. (a) Band structures of twisted bilayer graphene at the magic angle; (b)Wilson loops of the two flat bands from the K valley of twisted bilayer graphene (in $2{\text{π}}$).

下载: 全尺寸图片幻灯片

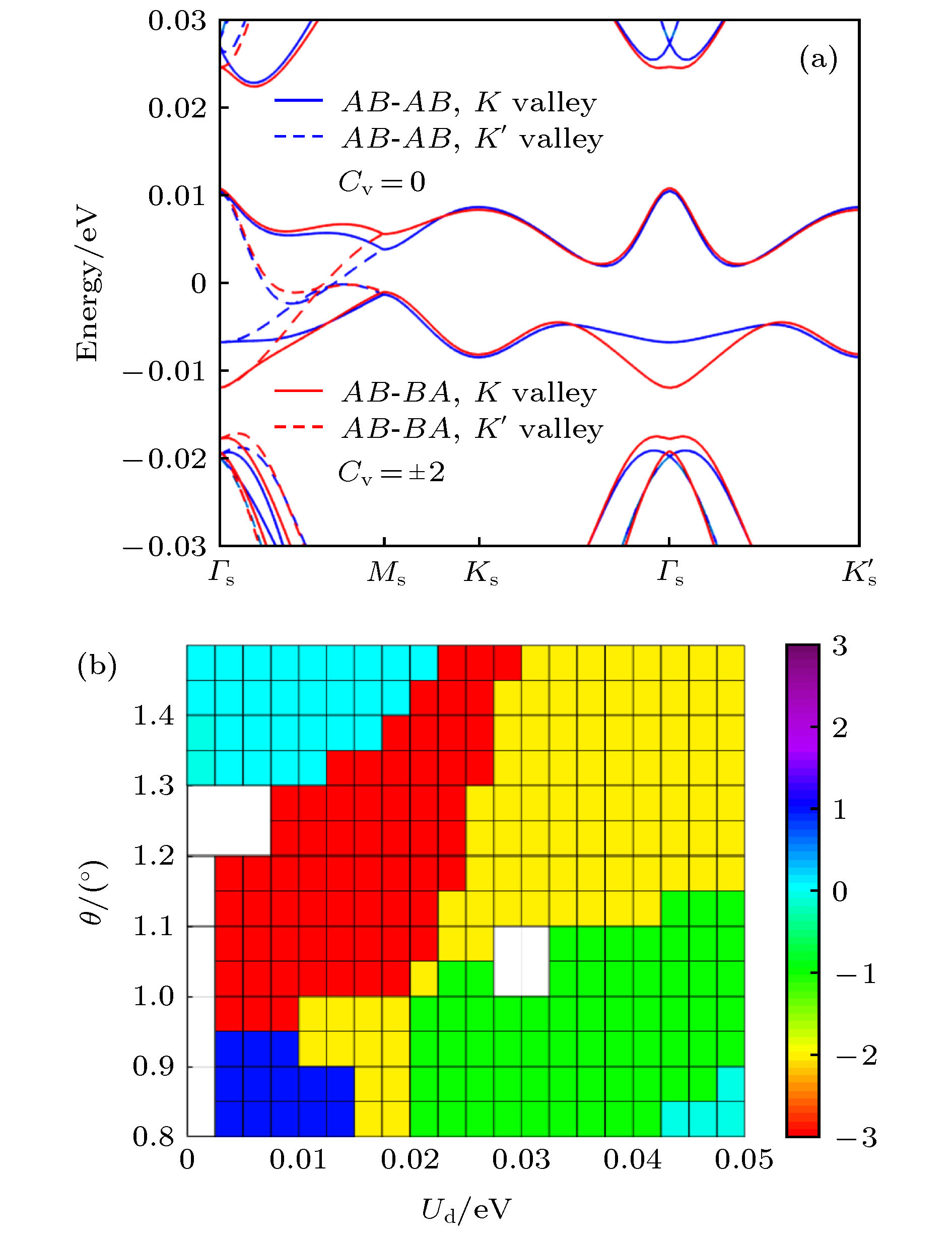
图 3 (a) 转角双层-双层石墨烯在$1.24 ^{\circ}$时的能带; (b) AB-AB堆垛的转角双层-双层石墨烯在$1.24 ^{\circ}$时K谷第一个导带陈数随转角$\theta$和垂直偏压$U_{\rm{d}}$的变化

Fig. 3. (a) Band structures of twisted double bilayer graphene at $\theta=1.24^{\circ}$; (b) the Chern number of the first conduction band for the K valley of AB-AB stacked twist-ed double bilayer graphene vs. the twist angle $\theta$ and vertical potential drop $U_{\rm{d}}$.

下载: 全尺寸图片幻灯片

图 4 魔角双层石墨烯平带对应的实空间电流密度分布　(a) K谷, $\varDelta_{\rm M}=0$; (b) $K'$谷, $\varDelta_{\rm M}=0$; (c) K谷, $\varDelta_{\rm M}=15\, {\rm{meV}}$; (d) $K'$谷, $\varDelta_{\rm M}=15\, {\rm{meV}}$, 图中黑色箭头代表电流方向, 颜色编码表示电流诱导的磁场强度, 单位为T

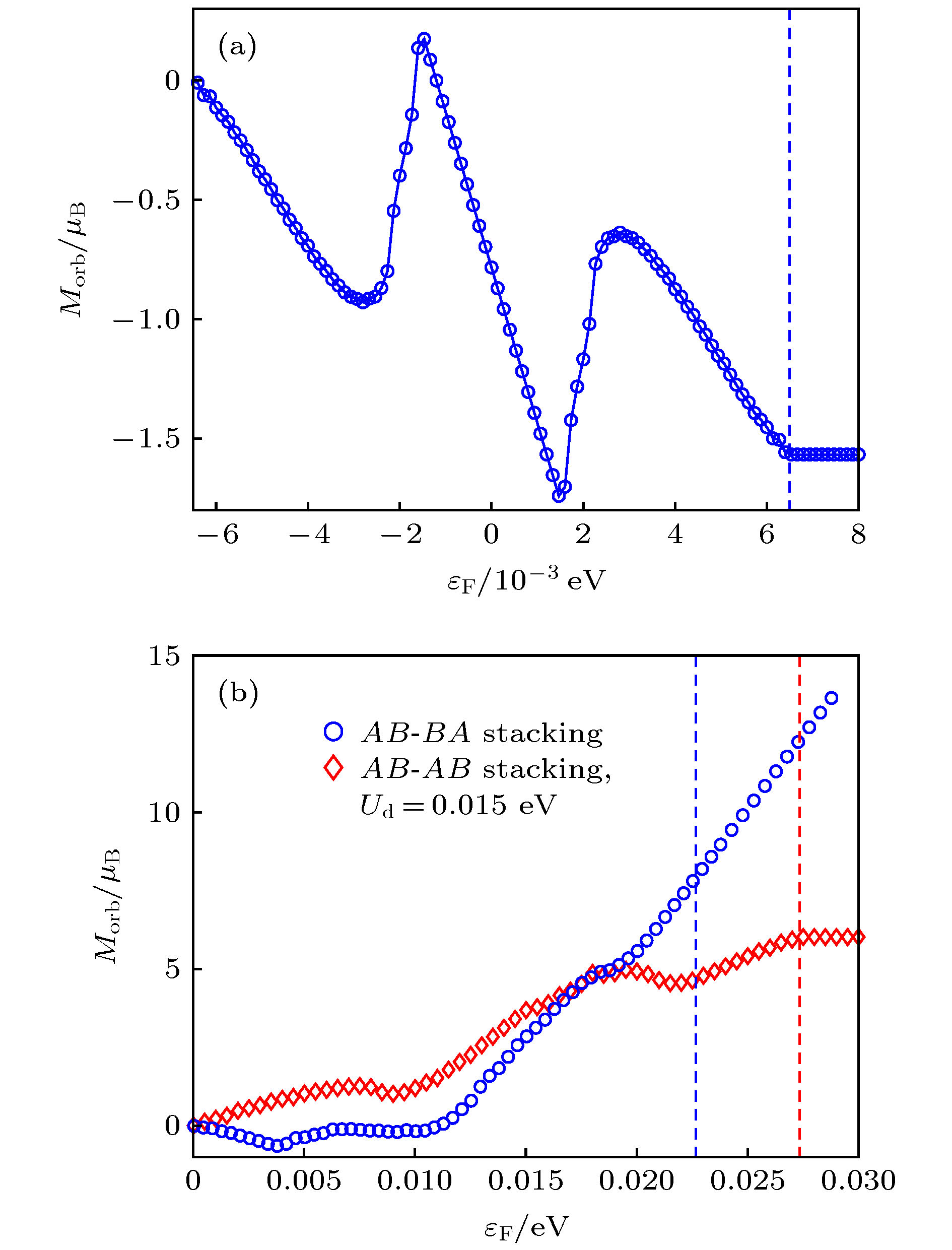
Fig. 4. Real-space current-density distribution contributed by the flat bands of magic-angle twisted bilayer graphene: (a) K valley, $\varDelta_{\rm M}=0$; (b) $K'$ valley, $\varDelta_{\rm M}=0$; (c) K valley, $\varDelta_{\rm M}=15\, {\rm{meV}}$; (d) $K'$ valley, $\varDelta_{\rm M}=15\, {\rm{meV}}$. The black arrows indicate the dire-ctions of the current density, and the color coding indicates the magnetic field induced by the current in unites of Tesla.

下载: 全尺寸图片幻灯片

图 5 (a)转角双层石墨烯在魔角时K谷平带贡献的轨道磁矩($M_ {\rm {orb}}$)随化学势 ($\varepsilon_{\rm{F}}$)的变化; (b)转角双层-双层石墨烯在$\theta=1.24^ {\circ}$时K谷平带贡献的轨道磁矩随化学势的变化

Fig. 5. (a) The orbital magnetization contributed by the flat bands of the K valley of twisted bilayer graphene at the magic angle; (b) the orbital magnetization contributed by the flat bands of K valley for twisted double bilayer graphene at $\theta=1.24^{\circ}$.

下载: 全尺寸图片幻灯片

表 1 由赝朗道能级图像推算出的魔角

Table 1. Magic angles derived from the pseudo Landau-level picture.

n 1 2 3 4 5

文献[4] 1.05° 0.50° 0.35° 0.24° 0.20°
(7)式 1.05° 0.52° 0.35° 0.26° 0.21°

下载: 导出CSV

map

[1]	Lopes dos Santos J M B, Peres N M R, Castro Neto A H 2007 Phys. Rev. Lett. 99 256802 Google Scholar
[2]	Mele E J 2010 Phys. Rev. B 81 161405 Google Scholar
[3]	Trambly de Laissardiere G, Mayou D, Magaud L 2010 Nano Lett. 10 804 Google Scholar
[4]	Bistritzer R, MacDonald A H 2011 Proc. Natl. Acad. Sci. 108 12233 Google Scholar
[5]	Lopes dos Santos J M B, Peres N M R, Castro Neto A H 2012 Phys. Rev. B 86 155449 Google Scholar
[6]	San-Jose P, González J, Guinea F 2012 Phys. Rev. Lett. 108 216802 Google Scholar
[7]	Cao Y, Fatemi V, Demir A, et al. 2018 Nature 556 80 Google Scholar
[8]	Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E, Jarillo-Herrero P 2018 Nature 556 43 Google Scholar
[9]	Yankowitz M, Chen S, Polshyn H, Zhang Y, Watanabe K, Taniguchi T, Graf D, Young A F, Dean C R 2019 Science 363 1059 Google Scholar
[10]	Sharpe A L, Fox E J, Barnard A W, Finney J, Watanabe K, Taniguchi T, Kastner M A, Goldhaber-Gordon D 2019 Science 365 605 Google Scholar
[11]	Serlin M, Tschirhart C, Polshyn H, Zhang Y, Zhu J, Watanabe K, Taniguchi T, Balents L, Young A 2019 Science 367 900
[12]	Stepanov P, Das I, Lu X, Fahimniya A, Watanabe K, Taniguchi T, Koppens F H, Lischner J, Levitov L, Efetov D K 2019 arXiv preprint arXiv: 1911.09198
[13]	Po H C, Zou L, Vishwanath A, Senthil T 2018 Phys. Rev. X 8 031089
[14]	Koshino M, Yuan N F Q, Koretsune T, Ochi M, Kuroki K, Fu L 2018 Phys. Rev. X 8 031087
[15]	Kang J, Vafek O 2018 Phys. Rev. X 8 031088
[16]	Isobe H, Yuan N F Q, Fu L 2018 Phys. Rev. X 8 041041
[17]	Xu X Y, Law K T, Lee P A 2018 Phys. Rev. B 98 121406 Google Scholar
[18]	Huang T, Zhang L, Ma T 2019 Sci. Bull. 64 310 Google Scholar
[19]	Liu C C, Zhang L D, Chen W Q, Yang F 2018 Phys. Rev. Lett. 121 217001 Google Scholar
[20]	Rademaker L, Mellado P 2018 Phys. Rev. B 98 235158 Google Scholar
[21]	Venderbos J W F, Fernandes R M 2018 Phys. Rev. B 98 245103 Google Scholar
[22]	Kang J, Vafek O 2019 Phys. Rev. Lett. 122 246401 Google Scholar
[23]	Xie M, MacDonald A H 2020 Phys. Rev. Lett. 124 097601 Google Scholar
[24]	Jian C M, Xu C 2018 arXiv preprint arXiv: 1810.03610
[25]	Bultinck N, Chatterjee S, Zaletel M P 2020 Phys. Rev. Lett. 124 166601 Google Scholar
[26]	Zhang Y H, Mao D, Senthil T 2019 Phys. Rev. Res. 1 033126 Google Scholar
[27]	Liu S, Khalaf E, Lee J Y, Vishwanath A 2019 arXiv preprint arXiv: 1905.07409
[28]	Wu F, Das Sarma S 2020 Phys. Rev. Lett. 124 046403 Google Scholar
[29]	Chatterjee S, Bultinck N, Zaletel M P 2020 Phys. Rev. B 101 165141 Google Scholar
[30]	Alavirad Y, Sau J D 2019 arXiv preprint arXiv: 1907.13633
[31]	Cécile R, Dong Z H, Zhang Y H, Senthil T 2020 Phys. Rev. Lett. 124 187601 Google Scholar
[32]	Bultinck N, Khalaf E, Liu S, Chatterjee S, Vishwanath A, Zaletel M P 2019 arXiv preprent, arXiv: 1911.02045
[33]	Angeli M, Tosatti E, Fabrizio M 2019 Phys. Rev. X 9 041010
[34]	Zhang Y, Jiang K, Wang Z, Zhang F 2020 arXiv preprint arXiv: 2001.02476
[35]	Lu C, Zhang Y, Zhang Y, Zhang M, Liu C C, Gu Z C, Chen W Q, Yang F 2020 arXiv preprint arXiv: 2003.09513
[36]	Po H C, Zou L, Senthil T, Vishwanath A 2019 Phys. Rev. B 99 195455 Google Scholar
[37]	Song Z, Wang Z, Shi W, Li G, Fang C, Bernevig B A 2019 Phys. Rev. Lett. 123 036401 Google Scholar
[38]	Yuan N F Q, Fu L 2018 Phys. Rev. B 98 045103 Google Scholar
[39]	Zou L, Po H C, Vishwanath A, Senthil T 2018 Phys. Rev. B 98 085435 Google Scholar
[40]	Liu J, Dai X 2019 arXiv preprint arXiv: 1911.03760
[41]	Shen C, Chu Y, Wu Q, Li N, Wang S, Zhao Y, Tang J, Liu J, Tian J, Watanabe K, Taniguchi T, Yang R, Meng Z Y, Shi D, Yazyev O V, Zhang G 2020 Nat. Phys. 16 520 Google Scholar
[42]	Liu X, Hao Z, Khalaf E, Lee J Y, Watanabe K, Taniguchi T, Vishwanath A, Kim P 2019 arXiv preprint arXiv: 1903.08130
[43]	Cao Y, Rodan-Legrain D, Rubies-Bigorda O, Park J M, Watanabe K, Taniguchi T, Jarillo-Herrero P 2020 Nature 583 215 Google Scholar
[44]	Chen G, Sharpe A L, Fox E J, et al. 2020 Nature 579 56 Google Scholar
[45]	Chen G, Sharpe A L, Gallagher P, Rosen I T, Fox E J, Jiang L, Lyu B, Li H, Watanabe K, Taniguchi T, Jung J, Shi Z, GoldhaberGordon D, Zhang Y, Wang F 2019 Nature 572 215 Google Scholar
[46]	Chen G, Jiang L, Wu S, et al. 2019 Nat. Phys. 15 237 Google Scholar
[47]	Zhang Y H, Mao D, Cao Y, Jarillo-Herrero P, Senthil T 2019 Phys. Rev. B 99 075127 Google Scholar
[48]	Liu J, Ma Z, Gao J, Dai X 2019 Phys. Rev. X 9 031021
[49]	Lee J Y, Khalaf E, Liu S, Liu X, Hao Z, Kim P, Vishwanath A 2019 Nat. Commun. 10 5333 Google Scholar
[50]	Chebrolu N R, Chittari B L, Jung J 2019 Phys. Rev. B 99 235417 Google Scholar
[51]	Cea T, Walet N R, Guinea F 2019 Nano Lett. 19 8683 Google Scholar
[52]	Koshino M 2019 Phys. Rev. B 99 235406 Google Scholar
[53]	Ma Z, Li S, Zheng Y W, Xiao M M, Jiang H, Gao J H, Xie X 2019 arXiv preprint arXiv: 1905.00622
[54]	Haddadi F, Wu Q, Kruchkov A J, Yazyev O V 2020 Nano Lett. 20 2410 Google Scholar
[55]	Li S Y, Zhang Y, Ren Y N, Liu J, Dai X, He L 2019 arXiv preprint arXiv: 1912.13133
[56]	Liu J, Dai X 2020 npj Comput. Mater. 6 57 Google Scholar
[57]	de Gail R, Goerbig M O, Guinea F, Montambaux G, Castro Neto A H 2011 Phys. Rev. B 84 045436 Google Scholar
[58]	Uchida K, Furuya S, Iwata J I, Oshiyama A 2014 Phys. Rev. B 90 155451 Google Scholar
[59]	Liu J, Liu J, Dai X 2019 Phys. Rev. B 99 155415 Google Scholar
[60]	Jung J, Raoux A, Qiao Z, MacDonald A H 2014 Phys. Rev. B 89 205414 Google Scholar
[61]	Moon P, Koshino M 2014 Phys. Rev. B 90 155406 Google Scholar
[62]	Zhang Y H, Mao D, Senthil T 2019 arXiv preprint arXiv: 1901.08209
[63]	Ahn J, Park S, Yang B J 2019 Phys. Rev. X 9 021013
[64]	Yu R, Qi X L, Bernevig A, Fang Z, Dai X 2011 Phys. Rev. B 84 075119 Google Scholar
[65]	Soluyanov A A, Vanderbilt D 2011 Phys. Rev. B 83 235401 Google Scholar
[66]	Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802 Google Scholar
[67]	Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 226801 Google Scholar
[68]	Fu L, Kane C L 2007 Phys. Rev. B 76 045302 Google Scholar
[69]	Castro Neto A H, Guinea F, Peres N M R, Novoselov K S, Geim A K 2009 Rev. Mod. Phys. 81 109 Google Scholar
[70]	Zhang Y H, Senthil T 2019 Phys. Rev. B 99 205150 Google Scholar
[71]	Chittari B L, Chen G, Zhang Y, Wang F, Jung J 2019 Phys. Rev. Lett. 122 016401 Google Scholar
[72]	McCann E, Koshino M 2013 Rep. Prog. Phys. 76 056503 Google Scholar
[73]	Thonhauser T, Ceresoli D, Vanderbilt D, Resta R 2005 Phys. Rev. Lett. 95 137205 Google Scholar
[74]	Ceresoli D, Thonhauser T, Vanderbilt D, Resta R 2006 Phys. Rev. B 74 024408 Google Scholar
[75]	Shi J, Vignale G, Xiao D, Niu Q 2007 Phys. Rev. Lett. 99 197202 Google Scholar
[76]	Choi Y, Kemmer J, Peng Y, et al. 2019 Nat. Phys. 15 1174 Google Scholar
[77]	Jiang Y, Lai X, Watanabe K, Taniguchi T, Haule K, Mao J, Andrei E Y 2019 Nature 573 91 Google Scholar
[78]	Nagaosa N, Sinova J, Onoda S, MacDonald A, Ong N 2010 Rev. Mod. Phys. 82 1539 Google Scholar
[79]	Fukumura T, Toyosaki H, Ueno K, Nakano M, Yamasaki T, Kawasaki M 2007 Jpn. J. Appl. Phys. 46 L642 Google Scholar
[80]	Sarma S D, Pinczuk A 2008 Perspectives in Quantum Hall Effects: Novel Quantum Liquids in Low-dimensional Semiconductor Structures (Hoboken: John Wiley & Sons)
[81]	Wu F, Lovorn T, Tutuc E, Martin I, MacDonald A H 2019 Phys. Rev. Lett. 122 086402 Google Scholar
[82]	Wu F, Lovorn T, Tutuc E, MacDonald A H 2018 Phys. Rev. Lett. 121 026402 Google Scholar
[83]	Wang L, Shih E M, Ghiotto A, et al. 2019 arXiv preprint arXiv: 1910.12147
[84]	Regan E C, Wang D, Jin C, et al. 2020 Nature 579 359 Google Scholar
[85]	An L, Cai X, Huang M, Wu Z, Lin J, Ying Z, Ye Z, Feng X, Wang N 2019 arXiv preprint arXiv: 1907.03966
[86]	Zhang Y, Yuan N F, Fu L 2019 arXiv preprint arXiv: 1910.14061
[87]	Lian B, Liu Z, Zhang Y, Wang J 2020 Phys. Rev. Lett. 124 126402 Google Scholar
[88]	Hejazi K, Luo Z X, Balents L 2020 Proc. Natl. Acad. Sci. 117 10721 Google Scholar

[1]	王玉, 梁钰林, 邢燕霞. 石墨烯中的拓扑安德森绝缘体相. , 2025, 74(4): 047301. doi: 10.7498/aps.74.20241031
[2]	王欢, 何春娟, 徐升, 王义炎, 曾祥雨, 林浚发, 王小艳, 巩静, 马小平, 韩坤, 王乙婷, 夏天龙. 拓扑半金属及磁性拓扑材料的单晶生长. , 2023, 72(3): 038103. doi: 10.7498/aps.72.20221574
[3]	刘义俊, 陈以威, 朱雨剑, 黄焱, 安冬冬, 李庆鑫, 甘祺康, 朱旺, 宋珺威, 王开元, 魏凌楠, 宗其军, 刘硕涵, 李世伟, 刘芝, 张琪, 徐瑛海, 曹新宇, 杨奥, 王浩林, 杨冰, Andy Shen, 于葛亮, 王雷. 转角双层-双层石墨烯中同位旋极化的C = 4陈绝缘态. , 2023, 72(14): 147303. doi: 10.7498/aps.72.20230497
[4]	白占斌, 王锐, 周亚洲, 吴天如, 葛建雷, 李晶, 秦宇远, 费付聪, 曹路, 王学锋, 王欣然, 张帅, 孙力玲, 宋友, 宋凤麒. 石墨烯中选择性增强Kane-Mele型自旋-轨道相互作用. , 2022, 71(6): 067202. doi: 10.7498/aps.71.20211815
[5]	郑玉强, 王世勇. 低维石墨烯体系中的离域磁性. , 2022, 71(18): 188101. doi: 10.7498/aps.71.20220895
[6]	白占斌, 王锐, 周亚洲, Tianru Wu（吴天如）, 葛建雷, 李晶, 秦宇远, 费付聪, 曹路, 王学锋, 王欣然, 张帅, 孙力玲, 宋友, 宋凤麒. 石墨烯中选择性增强Kane-Mele型自旋轨道相互作用. , 2021, (): . doi: 10.7498/aps.70.20211815
[7]	蔡潇潇, 罗国语, 李志强, 贺言. 转角双层石墨烯在应变下的光电导率. , 2021, 70(18): 187301. doi: 10.7498/aps.70.20210110
[8]	刘雨亭, 贺文宇, 刘军伟, 邵启明. 二维材料中贝里曲率诱导的磁性响应. , 2021, 70(12): 127303. doi: 10.7498/aps.70.20202132
[9]	徐贤达, 赵磊, 孙伟峰. 石墨烯纳米网电导特性的能带机理：第一原理计算. , 2020, 69(4): 047101. doi: 10.7498/aps.69.20190657
[10]	郗翔, 叶康平, 伍瑞新. 偏置磁场方向对磁性光子晶体能带结构的影响及其在构建拓扑边界态中的作用. , 2020, 69(15): 154102. doi: 10.7498/aps.69.20200198
[11]	吕新宇, 李志强. 石墨烯莫尔超晶格体系的拓扑性质及光学研究进展. , 2019, 68(22): 220303. doi: 10.7498/aps.68.20191317
[12]	张华林, 孙琳, 王鼎. 含单排线缺陷锯齿型石墨烯纳米带的电磁性质. , 2016, 65(1): 016101. doi: 10.7498/aps.65.016101
[13]	陈东海, 杨谋, 段后建, 王瑞强. 自旋轨道耦合作用下石墨烯pn结的电子输运性质. , 2015, 64(9): 097201. doi: 10.7498/aps.64.097201
[14]	徐雷, 戴振宏, 隋鹏飞, 王伟田, 孙玉明. 双空位掺杂氟化石墨烯的电子性质和磁性. , 2014, 63(18): 186101. doi: 10.7498/aps.63.186101
[15]	高潭华. 外来原子替代碳的氟化石墨烯的磁性和电子性质. , 2014, 63(4): 046102. doi: 10.7498/aps.63.046102
[16]	金峰, 张振华, 王成志, 邓小清, 范志强. 石墨烯纳米带能带结构及透射特性的扭曲效应. , 2013, 62(3): 036103. doi: 10.7498/aps.62.036103
[17]	林琦, 陈余行, 吴建宝, 孔宗敏. N掺杂对zigzag型石墨烯纳米带的能带结构和输运性质的影响. , 2011, 60(9): 097103. doi: 10.7498/aps.60.097103
[18]	高双红, 任兆玉, 郭平, 郑继明, 杜恭贺, 万丽娟, 郑琳琳. 石墨烯量子点的磁性及激发态性质. , 2011, 60(4): 047105. doi: 10.7498/aps.60.047105
[19]	王雪梅, 刘红. 锯齿型石墨烯纳米带的能带研究. , 2011, 60(4): 047102. doi: 10.7498/aps.60.047102
[20]	潘洪哲, 徐明, 陈丽, 孙媛媛, 王永龙. 单层正三角锯齿型石墨烯量子点的电子结构和磁性. , 2010, 59(9): 6443-6449. doi: 10.7498/aps.59.6443

计量

文章访问数: 17858
PDF下载量: 1464
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

转角石墨烯体系的拓扑特性和轨道磁性