磁电势垒结构中光场辅助电子自旋输运特性

李春雷; 徐燕; 郑军; 王小明; 袁瑞旸; 郭永

doi:10.7498/aps.69.20200237

摘要

基于Floquet理论和传输矩阵方法, 理论研究了光场对电子隧穿两类磁电垒结构的自旋极化输运特性的影响, 计算结果表明光场对两类磁电垒结构中电子的输运有显著影响: 首先, 原来不存在自旋过滤特性的结构应用光场后会产生低能区域明显的自旋过滤效应; 其次, 原来存在自旋过滤特性的结构应用光场后自旋过滤明显增强, 增幅超过一个数量级. 这些为新的自旋极化源的产生和自旋过滤现象的深入研究有一定的指导性意义.

关键词:

自旋过滤 /
自旋极化 /
磁电垒 /
光场

Abstract

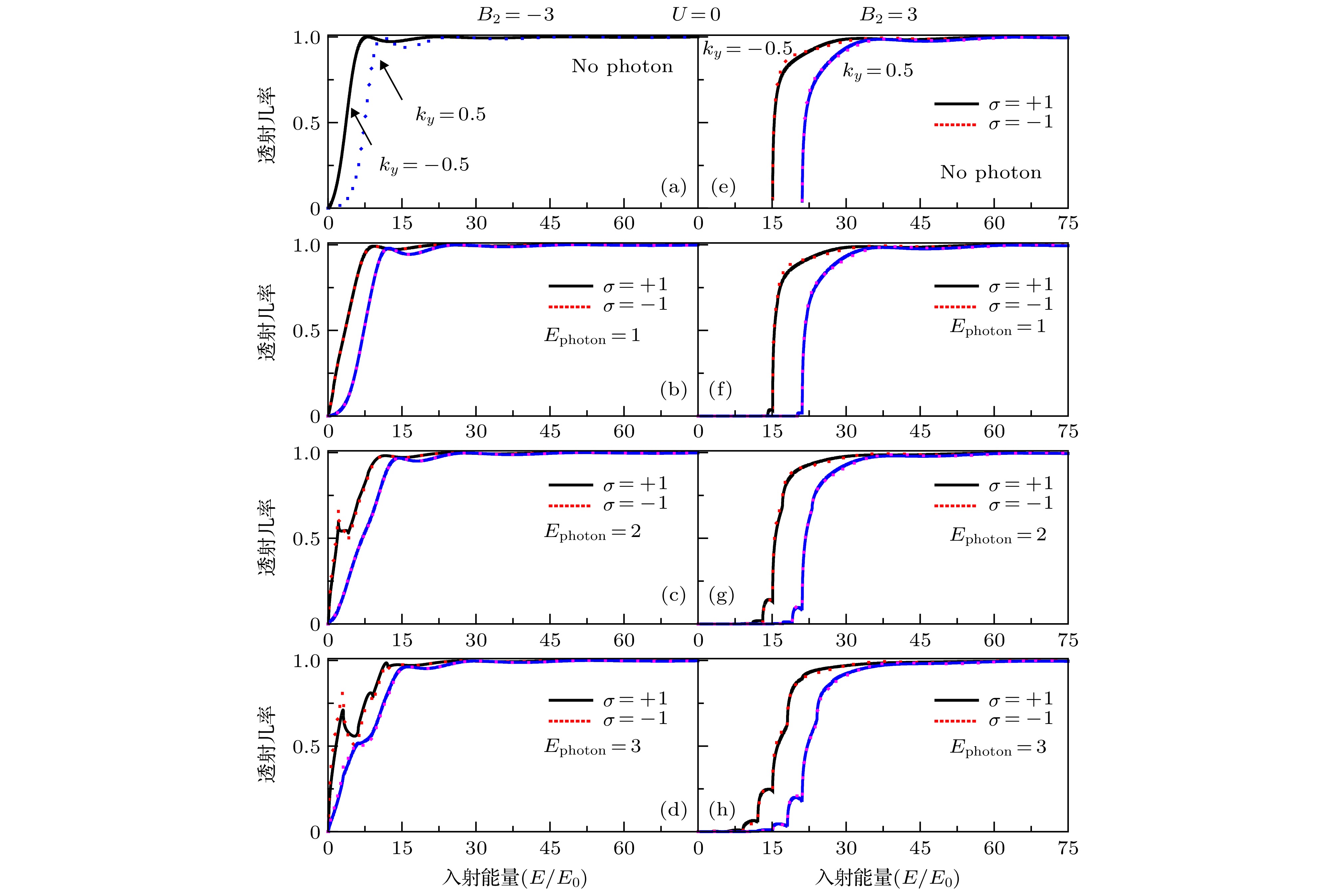
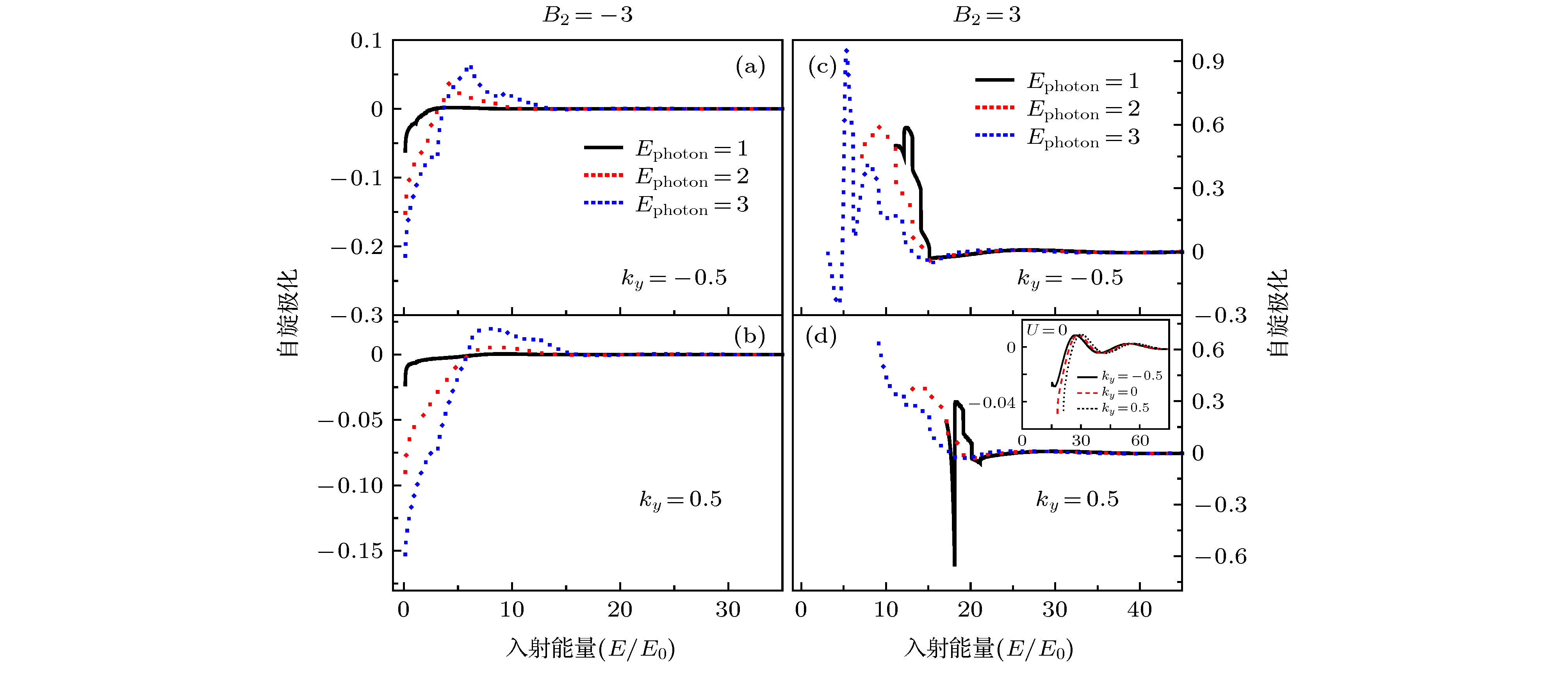
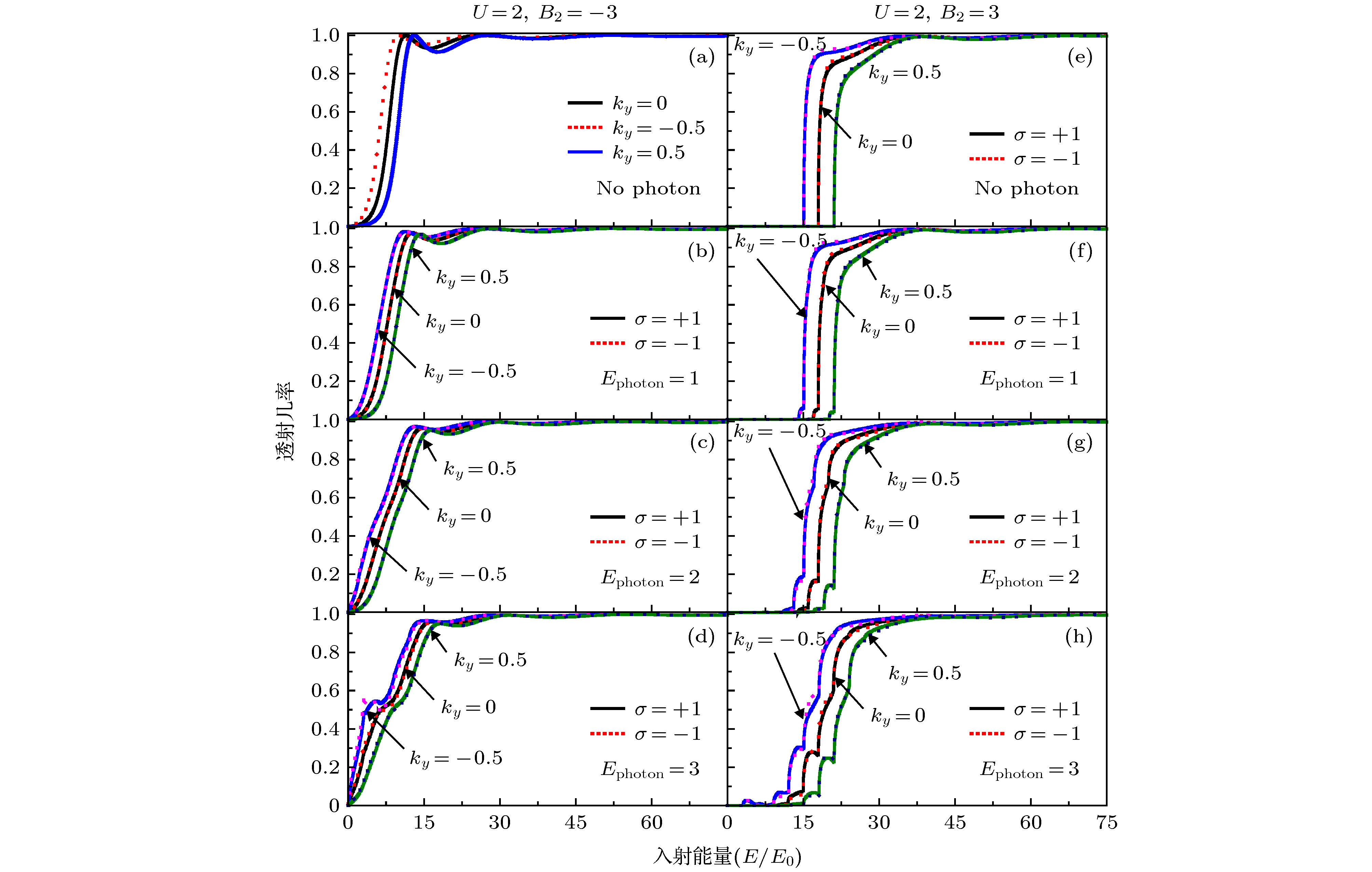
Based on the Floquet theory and transfer-matrix method, We investigated the influence of light-field on the spin-polarized transport properties for electrons tunneling through two kinds of magnetic-electric barrier structures (the $\delta$-doped magnetic-barrier can be realized in experiments by depositing two ferromagnetic stripes on top and bottom of a semiconductor heterostructure and the light-field can be realized by placing a hemispherical silicon lens on the back surface of the semiconductor substrate). Transport properties result from the interaction of electrons with the light-field by means of photon absorption and emission. It is found that the light-field can greatly affect the transmission probabilities as well as the corresponding polarizations. The distance between the adjacent peaks and the number of the transport peaks can be controlled by adjusting the frequency and the amplitude of the light-field, respectively. It is shown that a significant spin-polarization effect can be induced by such light-field in the kind of antisymmetric magnetic barrier structure ($B_{1}=-B_{2}$) and the light-field can greatly change the spin-polarization effect in the kind of symmetric magnetic barrier structure ($B_{1}=B_{2}$). When the frequency of the light-field increases, the spin-polarization shifts toward the low-energy end and gradually increases. These remarkable properties of spin polarization may be beneficial for the devising tunable spin filtering devices.

Keywords:

作者及机构信息

1.
首都师范大学初等教育学院, 北京　100048

2.
渤海大学数理学院, 锦州　121013

3.
中国地质大学附属中学, 北京　100083

4.
首都师范大学物理系, 北京　100048

5.
清华大学物理系, 低维量子物理国家重点实验室, 北京　100084

6.
量子物质科学协同创新中心, 北京　100084

通信作者: 李春雷, licl@cnu.edu.cn

基金项目: 国家级-国家自然科学基金(11574173)

Authors and contacts

1.
College of Elementary Education, Capital Normal University, Beijing 100048, China

2.
College of Mathematics and Physics, Bohai University, Jinzhou 121013, China

3.
Middle School Affiliated to China University of Geosciences, Beijing 100083, China

4.
Department of Physics, Capital Normal University, Beijing 100048, China

5.
State Key Laboratory of Low-Dimensional Quantum Physics, Department of Physics, Tsinghua University, Beijing 100084, China

6.
Collaborative Innovation Center of Quantum Matter, Beijing 100084, China

Corresponding author: Li Chun-Lei, licl@cnu.edu.cn

文章全文 : translate this paragraph

参考文献

[1]	Dubrovin B A, Novikov S P 1980 Sov. Phys. JETP 3 511
[2]	Vil'ms P P, Entin M V 1988 Sov. Phys. Semicond. 22 1209
[3]	Yoshioka D, Iye Y 1987 J. Phys. Soc. Jpn. 56 448 Google Scholar
[4]	Peeters F M, Matulis A, Ibrahim I S 1996 Physica B: Condensed Matter 227 131 Google Scholar
[5]	Ibrahim I S, Peeters F M 1995 Phys. Rev. B 52 17321 Google Scholar
[6]	Guo Y, Gu B L, Duan W H, Zhang Y 1997 Phys. Rev. B 55 9314 Google Scholar
[7]	Guo Y, Gu B L, Li Z Q, Yu J Z, Kawazoe Y 1998 J. Appl. Phys. 83 4545 Google Scholar
[8]	Guo Y, Gu B L, Li Z Q, Zhu J L, Kawazoe Y 1998 J. Phys. Condens. Matter 10 1549 Google Scholar
[9]	Guo Y, Wang H, Gu B L, Kawazoe Y 2000 Phys. Rev. B 61 1728 Google Scholar
[10]	Guo Y, Gu B L, Zeng Z, Yu J Z, Kawazoe Y 2000 Phys. Rev. B 62 2635 Google Scholar
[11]	Guo Y, Zhai F, Gu B L, Kawazoe Y 2002 Phys. Rev. B 66 045312 Google Scholar
[12]	Papp G, Peeters F M 2001 Appl. Phys. Lett. 78 2184 Google Scholar
[13]	Xu H Z, Okada Y 2001 Appl. Phys. Lett. 79 3119 Google Scholar
[14]	Jiang Y, Jalil M B A, Low T S 2002 Appl. Phys. Lett. 80 1673 Google Scholar
[15]	秦建华, 郭永, 陈信义, 顾秉林 2003 52 2569 Google Scholar Qin J H, Guo Y, Chen X Y, Gu B L 2003 Acta Phys. Sin. 52 2569 Google Scholar
[16]	Lu M W, Wang Z Y, Liang Y L, An Y B, Li Q L 2013 Appl. Phys. Lett. 102 022410 Google Scholar
[17]	Lu M W, Wang Z Y, Liang Y L, An Y B, Li Q L 2013 Euro. Phys. Lett. 101 47001 Google Scholar
[18]	Lu M W, Wang Z Y, Cao X L, Li S 2013 Solid State Commun. 165 45 Google Scholar
[19]	Li S, Lu M W, Jiang Y Q, Chen S Y 2014 AIP Adv. 4 097112 Google Scholar
[20]	Lu M W, Cao X L, Huang X H, Jiang Y Q, Li S 2014 J. Appl. Phys. 115 174305 Google Scholar
[21]	Li C L, Xu Y 2010 Chin. Phys. B 19 057202 Google Scholar
[22]	张存喜, 王瑞, 孔令民 2010 59 4980 Google Scholar Zhang C X, Wang R, Kong L M 2010 Acta Phys. Sin. 59 4980 Google Scholar
[23]	Zhang C X, Wang R, Nie Y H, Liang J Q 2008 Chin. Phys. B 17 2662 Google Scholar
[24]	Li C L, Ruan R Y, Guo Y 2016 J. Appl. Phys. 119 014306 Google Scholar
[25]	Dayem A H, Martin R J 1962 Phys. Rev. Lett. 8 246 Google Scholar
[26]	Tien P K, Gordon J P 1963 Phys. Rev. 129 647 Google Scholar
[27]	Prez delValle C, Lefebvre R, Atabek O 1999 Phys. Rev. A 59 3701 Google Scholar
[28]	Runge E, Ehrenreich H 1992 Phys. Rev. B 45 9145 Google Scholar
[29]	Sun Q F, Wang J, Lin T H 2000 Phys. Rev. B 61 12643 Google Scholar
[30]	Bruder C, Schoeller H 1994 Phys. Rev. Lett. 72 1076 Google Scholar
[31]	Shibata K, Umeno A, Cha K M, Hirakawa K 2012 Phys. Rev. Lett. 109 077401 Google Scholar
[32]	Schoelkopf R J, Kozhevnikov A A, Prober D E 1998 Phys. Rev. Lett. 80 2437 Google Scholar
[33]	Burmeister G, Maschke K 1998 Phys. Rev. B 57 13050 Google Scholar
[34]	Li W J, Reichl L E 1999 Phys. Rev. B 60 15732 Google Scholar
[35]	曾谨言 2000 量子力学 (卷I) (北京: 科学出版社) 第117页 Zeng J Y 2000 Quantum Mechanics (Vol. 1) (Beijing: Science Press) p117 (in Chinese)

施引文献

图 1 光场$ V_{1}\cos(\omega t) $调制下两类磁电垒结构　(a)反向等强度$ {\text{δ}} $型磁电垒结构; (b)同向等强度$ {\text{δ}} $型磁电垒结构

Fig. 1. The model field-driven magnetic-electric barrier structures: (a) $ B_{1} = -B_{2} $; (b) $ B_{1} = B_{2} $

下载: 全尺寸图片幻灯片

图 2 电子隧穿磁垒结构透射几率谱　(a)−(d)反向等强度$ {\text{δ}} $型磁垒结构; (e)−(h)同向等强度$ {\text{δ}} $型磁垒结构

Fig. 2. Transmission probabilities as the function of the incident energy: (a)−(d)$ B_{1} = -B_{2} = 3 $; (e)−(h)$ B_{1} = B_{2} = 3 $

下载: 全尺寸图片幻灯片

图 3 自旋极化度随入射能量的变化　(a)−(b) $ B_{1} = -B_{2} $; (c)−(d) $ B_{1} = B_{2} $

Fig. 3. Spin polarization as the function of the incident energy: (a)−(b) $ B_{1} = -B_{2} $; (c)−(d) $ B_{1} = B_{2} $

下载: 全尺寸图片幻灯片

图 4 电子隧穿磁电垒结构透射几率谱　(a)−(d) $ B_{1} = -B_{2} $; (e)−(h) $ B_{1} = B_{2} $

Fig. 4. Transmission probabilities as the function of the incident energy: (a)−(d) $ B_{1} = -B_{2} $; (e)−(h) $ B_{1} = B_{2} $

下载: 全尺寸图片幻灯片

图 5 自旋极化度随入射能量的变化关系　(a)−(c) $ B_{1} = -B_{2} $; (d)−(f) $ B_{1} = B_{2} $

Fig. 5. Spin polarization as the function of the incident energy: (a)−(c) $ B_{1} = -B_{2} $; (d)−(f) $ B_{1} = B_{2} $

下载: 全尺寸图片幻灯片

map

[1]	Dubrovin B A, Novikov S P 1980 Sov. Phys. JETP 3 511
[2]	Vil'ms P P, Entin M V 1988 Sov. Phys. Semicond. 22 1209
[3]	Yoshioka D, Iye Y 1987 J. Phys. Soc. Jpn. 56 448 Google Scholar
[4]	Peeters F M, Matulis A, Ibrahim I S 1996 Physica B: Condensed Matter 227 131 Google Scholar
[5]	Ibrahim I S, Peeters F M 1995 Phys. Rev. B 52 17321 Google Scholar
[6]	Guo Y, Gu B L, Duan W H, Zhang Y 1997 Phys. Rev. B 55 9314 Google Scholar
[7]	Guo Y, Gu B L, Li Z Q, Yu J Z, Kawazoe Y 1998 J. Appl. Phys. 83 4545 Google Scholar
[8]	Guo Y, Gu B L, Li Z Q, Zhu J L, Kawazoe Y 1998 J. Phys. Condens. Matter 10 1549 Google Scholar
[9]	Guo Y, Wang H, Gu B L, Kawazoe Y 2000 Phys. Rev. B 61 1728 Google Scholar
[10]	Guo Y, Gu B L, Zeng Z, Yu J Z, Kawazoe Y 2000 Phys. Rev. B 62 2635 Google Scholar
[11]	Guo Y, Zhai F, Gu B L, Kawazoe Y 2002 Phys. Rev. B 66 045312 Google Scholar
[12]	Papp G, Peeters F M 2001 Appl. Phys. Lett. 78 2184 Google Scholar
[13]	Xu H Z, Okada Y 2001 Appl. Phys. Lett. 79 3119 Google Scholar
[14]	Jiang Y, Jalil M B A, Low T S 2002 Appl. Phys. Lett. 80 1673 Google Scholar
[15]	秦建华, 郭永, 陈信义, 顾秉林 2003 52 2569 Google Scholar Qin J H, Guo Y, Chen X Y, Gu B L 2003 Acta Phys. Sin. 52 2569 Google Scholar
[16]	Lu M W, Wang Z Y, Liang Y L, An Y B, Li Q L 2013 Appl. Phys. Lett. 102 022410 Google Scholar
[17]	Lu M W, Wang Z Y, Liang Y L, An Y B, Li Q L 2013 Euro. Phys. Lett. 101 47001 Google Scholar
[18]	Lu M W, Wang Z Y, Cao X L, Li S 2013 Solid State Commun. 165 45 Google Scholar
[19]	Li S, Lu M W, Jiang Y Q, Chen S Y 2014 AIP Adv. 4 097112 Google Scholar
[20]	Lu M W, Cao X L, Huang X H, Jiang Y Q, Li S 2014 J. Appl. Phys. 115 174305 Google Scholar
[21]	Li C L, Xu Y 2010 Chin. Phys. B 19 057202 Google Scholar
[22]	张存喜, 王瑞, 孔令民 2010 59 4980 Google Scholar Zhang C X, Wang R, Kong L M 2010 Acta Phys. Sin. 59 4980 Google Scholar
[23]	Zhang C X, Wang R, Nie Y H, Liang J Q 2008 Chin. Phys. B 17 2662 Google Scholar
[24]	Li C L, Ruan R Y, Guo Y 2016 J. Appl. Phys. 119 014306 Google Scholar
[25]	Dayem A H, Martin R J 1962 Phys. Rev. Lett. 8 246 Google Scholar
[26]	Tien P K, Gordon J P 1963 Phys. Rev. 129 647 Google Scholar
[27]	Prez delValle C, Lefebvre R, Atabek O 1999 Phys. Rev. A 59 3701 Google Scholar
[28]	Runge E, Ehrenreich H 1992 Phys. Rev. B 45 9145 Google Scholar
[29]	Sun Q F, Wang J, Lin T H 2000 Phys. Rev. B 61 12643 Google Scholar
[30]	Bruder C, Schoeller H 1994 Phys. Rev. Lett. 72 1076 Google Scholar
[31]	Shibata K, Umeno A, Cha K M, Hirakawa K 2012 Phys. Rev. Lett. 109 077401 Google Scholar
[32]	Schoelkopf R J, Kozhevnikov A A, Prober D E 1998 Phys. Rev. Lett. 80 2437 Google Scholar
[33]	Burmeister G, Maschke K 1998 Phys. Rev. B 57 13050 Google Scholar
[34]	Li W J, Reichl L E 1999 Phys. Rev. B 60 15732 Google Scholar
[35]	曾谨言 2000 量子力学 (卷I) (北京: 科学出版社) 第117页 Zeng J Y 2000 Quantum Mechanics (Vol. 1) (Beijing: Science Press) p117 (in Chinese)

计量

文章访问数: 6471
PDF下载量: 94
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

磁电势垒结构中光场辅助电子自旋输运特性