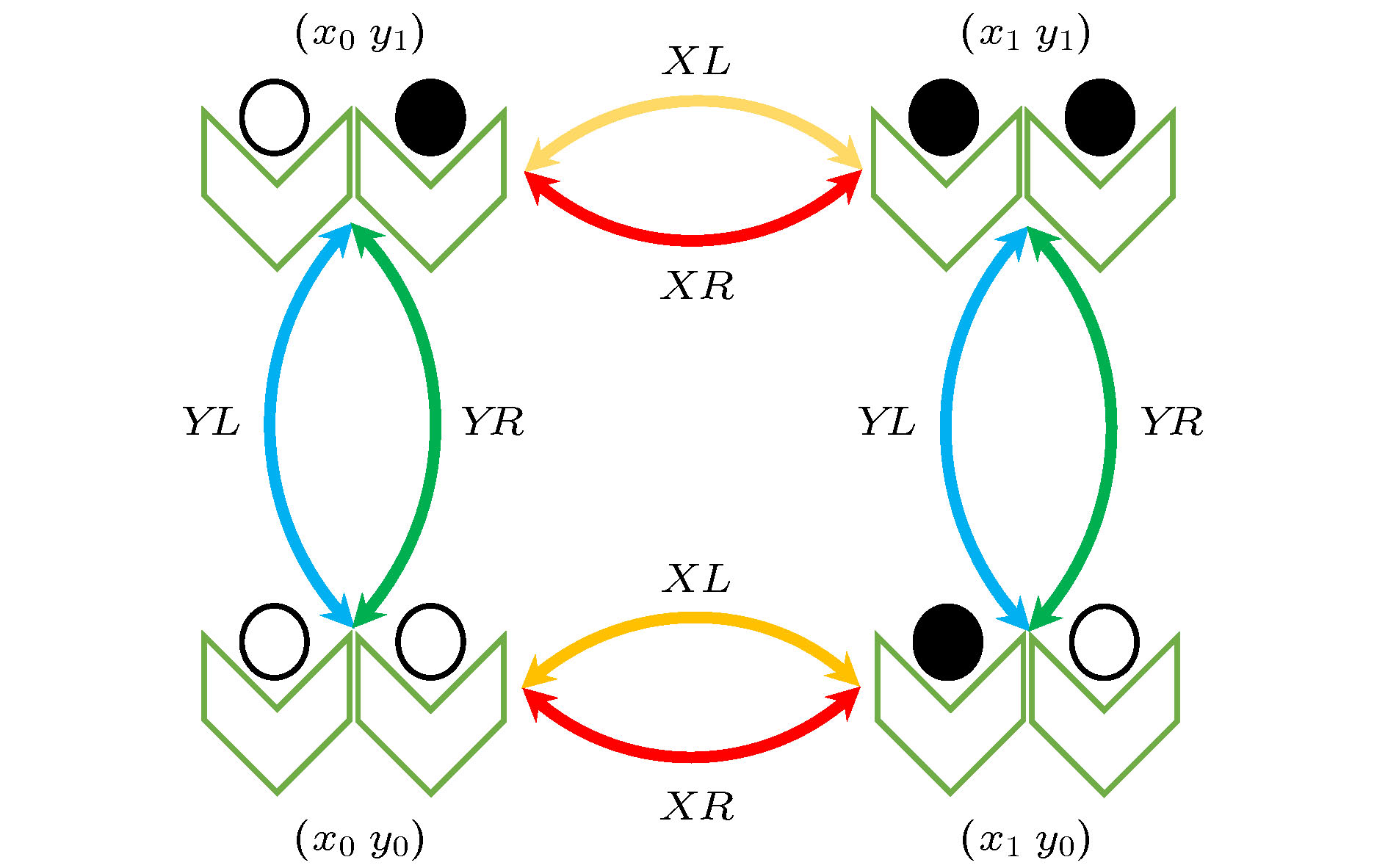
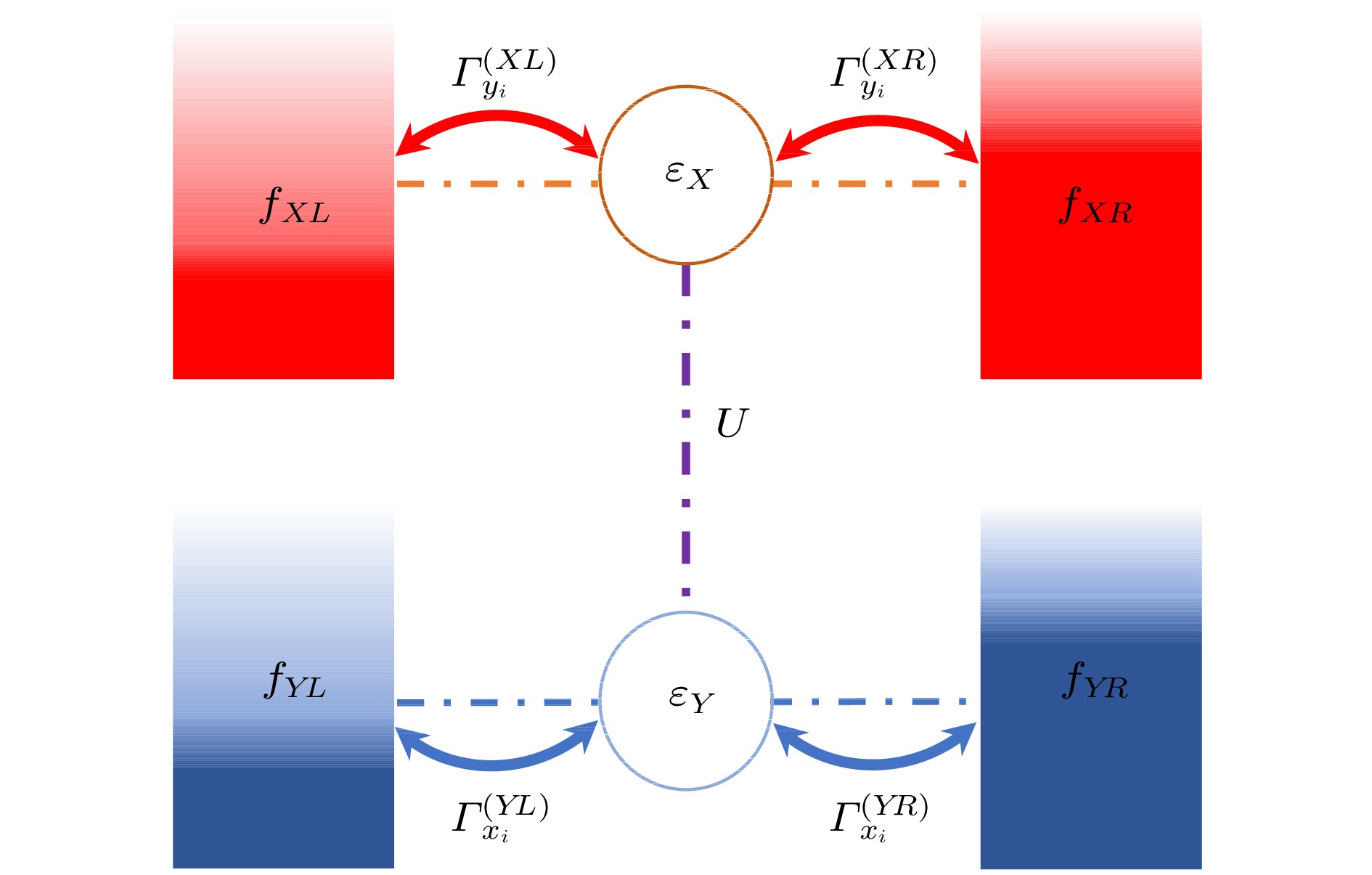
-
In thermodynamics of irreversible processes, the entropy production rate (EPR) is usually generated by the rate of the entropy change of the system due to its internal transitions and the entropy flows due to the interactions between the system and the environment. For the bipartite system, in addition to the factors mentioned above, the energy and information exchanges between the two subsystems will generate an additional entropy production in the EPR of a subsystem. To reveal the essence and role of the information flow, we build an open dissipative quantum system coupled to multiple electronic reservoirs with the same temperature and different chemical potentials. Based on the thermal and electron transport properties of a double quantum-dot system with Coulomb coupling, the EPR of each quantum dot and the information flow between subsystems are studied. Starting from the quantum master equation under the Born, Markov, and rotating-wave (or secular) approximations, we derive the EPRs of the total system and subsystems at the steady state. For purposes of relating the thermodynamic properties to the fundamental fluxes and affinities, a graph representation of the dynamics of the four-state model is introduced. Selecting a directed graph and a complete set of basic cycles by using Schnakenberg’s network theory, we show how the EPRs of the total system and the subsystems relate to global and local cycle fluxes. It is found that the energy and information exchanges between the quantum dots depend on the global cycle flux. The EPRs induced by the electron flows due to the chemical potential difference as well as the energy and information exchanges between the subsystems are the key elements of thermodynamic irreversibilities. The EPRs caused by the information exchange guarantee the continuous electron transports. The EPRs and the coarse-grained EPRs of the subsystems varying with the Coulomb coupling strength are obtained numerically. The results demonstrate that the information flows in the process of internal exchange become important to fully understand the operation mechanism of the bipartite system. Without violating the second law of thermodynamics, the information can be regarded as a driving force to move electrons from low to high chemical potential.
-
Keywords:
- principle of entropy increase /
- double quantum-dot system /
- energy flow /
- information flow
[1] 吴联仁, 李瑾颉, 齐佳音 2019 68 078901
Google Scholar
Wu L R, Li J J, Qi J J 2019 Acta Phys. Sin. 68 078901
Google Scholar
[2] 陈俊, 於亚飞, 张智明 2015 64 160305
Google Scholar
Chen J, Yu Y F, Zhang Z M 2015 Acta Phys. Sin. 64 160305
Google Scholar
[3] 孙昌璞, 全海涛 2013 物理 42 756
Sun C P, Quan H T 2013 Physics 42 756
[4] Quan H T, Wang Y D, Liu Y, Sun C P, Nori F 2006 Phys. Rev. Lett. 97 180402
Google Scholar
[5] Cottet N, Jezouin S, Bretheau L, Campagne-lbarcq P, Ficheux Q, Aufers J, Auffèves A, Azouit R, Rouchon P, Huard B 2017 Proc. Natl. Acad. Sci. U.S.A. 114 7561
Google Scholar
[6] Park J, Kim K, Sagawa T, Kim S 2013 Phys. Rev. Lett. 111 230402
Google Scholar
[7] Paneru G, Lee D, Tlusty T, Pak H 2018 Phys. Rev. Lett. 120 020601
Google Scholar
[8] Dong H, Xu D Z, Cai C Y, Sun C P 2011 Phys. Rev. E 83 061108
Google Scholar
[9] Cai C Y, Dong H, Sun C P 2012 Phys. Rev. E 85 031114
Google Scholar
[10] Toyabe S, Sagawa T, Ueda M, Muneyuki E, Sano M 2010 Nat. Phys. 6 988
Google Scholar
[11] Lebedev A V, Lesovik G B, Vinokur V M, Blatter G 2018 Phys. Rev. B 98 214502
Google Scholar
[12] Naghiloo M, Alonso J J, Romito A, Lutz E, Murch K W 2018 Phys. Rev. Lett. 121 030604
Google Scholar
[13] Schaller G, Cerrillo J, Engelhardt G, Strasberg P 2018 Phys. Rev. B 97 195104
Google Scholar
[14] Jacobs K 2009 Phys. Rev. A 80 012322
Google Scholar
[15] Granger L, Kantz H 2011 Phys. Rev. E 84 061110
Google Scholar
[16] Sagawa T, Ueda M 2008 Phys. Rev. Lett. 100 080403
Google Scholar
[17] Koch-Janusz M, Ringel Z 2018 Nat. Phys. 14 578
Google Scholar
[18] Mehta P, Lang A H, Schwab D J 2016 J. Stat. Phys. 162 1153
Google Scholar
[19] Ito S, Sagawa T 2015 Nat. Commun. 6 7498
Google Scholar
[20] Barato A C, Hartich D, Seifert U 2014 New J. Phys. 16 103024
Google Scholar
[21] Mehta P, Schwab D J 2012 Proc. Natl. Acad. Sci. U.S.A. 109 17978
Google Scholar
[22] 李唯, 符婧, 杨贇贇, 何济洲 2019 68 220501
Google Scholar
Li W, Fu J, Yang Y Y, He J Z 2019 Acta Phys. Sin. 68 220501
Google Scholar
[23] 何弦, 何济洲, 肖宇玲 2012 61 150302
Google Scholar
He X, He J Z, Xiao Y L 2012 Acta Phys. Sin. 61 150302
Google Scholar
[24] Horowitz J M, Esposito M 2014 Phys. Rev. X 4 031015
[25] Barato A C, Hartich D, Seifert U 2014 New Journal of Physics 16 103024
[26] Yamamoto S, Ito S, Shiraishi N, Sagawa T 2016 Phys. Rev. E 94 052121
[27] Ptaszyński K, Esposito M 2019 Phys. Rev. Lett. 122 150603
Google Scholar
[28] Strasberg P, Schaller G, Brandes T, Esposito M 2017 Phys. Rev. X 7 021003
[29] Schnakenberg J 1976 Rev. Mod. Phys. 48 571
Google Scholar
[30] Breuer H P, Petruccione F 2001 The Theory of Open Quantum Systems (Oxford: Oxford University Press) pp110–149
[31] Schaller G 2014 Open Quantum Systems Far from Equilibrium (New York: Springer) pp73–74
[32] Spohn H 1978 J. Math. Phys. 19 1227
Google Scholar
[33] Esposito M, Harbola U, Mukamel S 2009 Rev. Mod. Phys. 81 1665
Google Scholar
[34] Thulasiraman K, Swamy M N S 1997 Graphs: Theory and Algorithms (New York: John Wiley & Sons) pp1–26
[35] Sagawa T, Ueda M 2013 New J. Phys. 15 125012
Google Scholar
[36] Bauer M, Abreu D, Seifert U 2012 J. Phys. A: Math. Theor. 45 162001
Google Scholar
[37] Ito S, Sagawa T 2013 Phys. Rev. Lett. 111 180603
Google Scholar
-
图 1 库仑耦合双量子点非平衡系统
Fig. 1. The nonequilibrium double quantum-dot system with Coulomb coupling.
图 2 库仑耦合双量子点系统的状态点和跃迁模式
Fig. 2. The states and transition modes of the double quantum-dot system with Coulomb coupling.
图 3 四态模型的有向图及其基本循环
Fig. 3. The directed graph of the four-state model and its cycle basis.
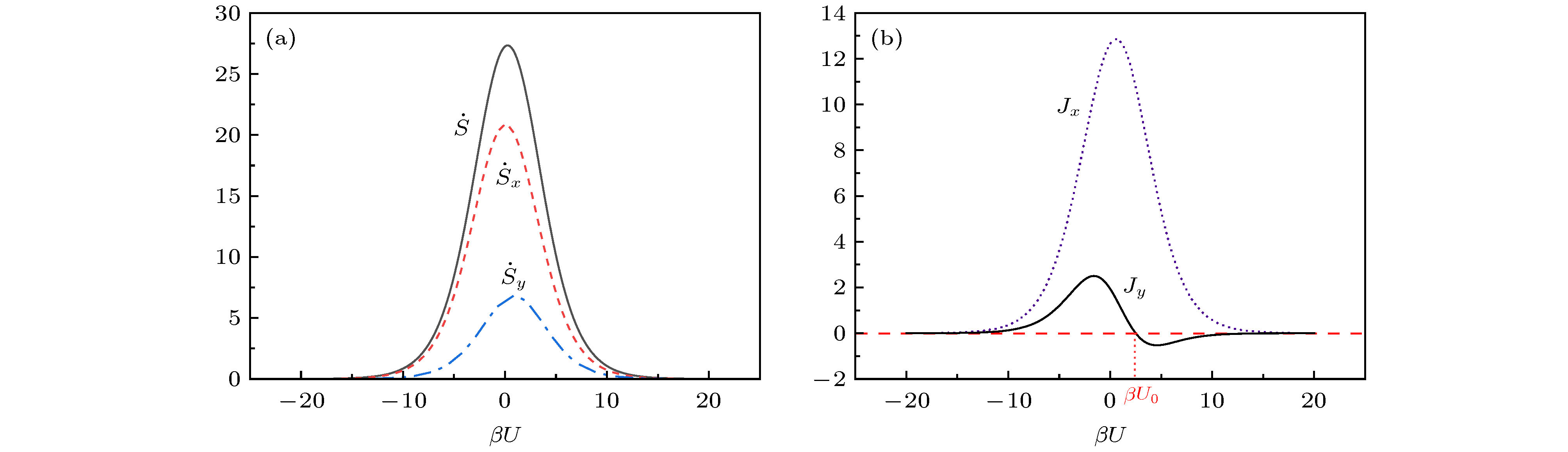
图 4 (a)熵产生率
${\dot S_{\rm{T}}}$ ,${\dot S_X}$ 和${\dot S_Y}$ 及(b)电子流${J_X}$ 和${J_Y}$ 随库仑耦合强度的变化曲线. 其中$\beta \Delta {\mu _X} = 2$ ,$\beta \Delta {\mu _Y} = 1$ ,$ \delta =\varDelta =1 $ ,${\varepsilon _X} = \dfrac{{\left( {{\mu _{XR}} + {\mu _{XL}}} \right)}}{2} - \dfrac{U}{2}$ ,${\varepsilon _Y} = \dfrac{{\left( {{\mu _{YR}} + {\mu _{YL}}} \right)}}{2} - \dfrac{U}{2}$ Fig. 4. (a) The entropy production rates
${\dot S_{\rm{T}}}$ ,${\dot S_X}$ , and${\dot S_Y}$ , and (b) the curves of the electron flows${J_X}$ and${J_Y}$ varying with the Coulomb coupling strength, where$\beta \Delta {\mu _X} = 2$ ,$\beta \Delta {\mu _Y} = 1$ ,$\delta \!=\!\varDelta \!=\!1$ ,${\varepsilon _X} \!=\! \dfrac{{\left( {{\mu _{XR}} + {\mu _{XL}}} \right)}}{2} \!-\! \dfrac{U}{2}$ , and${\varepsilon _Y} \!=\! \dfrac{{\left( {{\mu _{YR}} + {\mu _{YL}}} \right)}}{2} - \dfrac U2$ 
图 5 部分熵产生率
${\dot S_{{\mu _i}}}$ ,${\dot S_{{U_i}}}$ 和${\dot I_i}\left( {i = X, Y} \right)$ 随库仑耦合强度的变化曲线.Fig. 5. The curves of the partial entropy production rates
${\dot S_{{\mu _i}}}$ ,${\dot S_{{U_i}}}$ , and${\dot I_i}\left( {i = X, Y} \right)$ varying with the Coulomb coupling strength.
图 6 粗粒化熵产生率
${\sigma _i}\left( {i = X, Y} \right)$ 随库仑耦合强度变化曲线Fig. 6. The curves of the coarse-grained entropy production rates
${\sigma _i}\left( {i = X, Y} \right)$ varying with the Coulomb coupling strength. -
[1] 吴联仁, 李瑾颉, 齐佳音 2019 68 078901
Google Scholar
Wu L R, Li J J, Qi J J 2019 Acta Phys. Sin. 68 078901
Google Scholar
[2] 陈俊, 於亚飞, 张智明 2015 64 160305
Google Scholar
Chen J, Yu Y F, Zhang Z M 2015 Acta Phys. Sin. 64 160305
Google Scholar
[3] 孙昌璞, 全海涛 2013 物理 42 756
Sun C P, Quan H T 2013 Physics 42 756
[4] Quan H T, Wang Y D, Liu Y, Sun C P, Nori F 2006 Phys. Rev. Lett. 97 180402
Google Scholar
[5] Cottet N, Jezouin S, Bretheau L, Campagne-lbarcq P, Ficheux Q, Aufers J, Auffèves A, Azouit R, Rouchon P, Huard B 2017 Proc. Natl. Acad. Sci. U.S.A. 114 7561
Google Scholar
[6] Park J, Kim K, Sagawa T, Kim S 2013 Phys. Rev. Lett. 111 230402
Google Scholar
[7] Paneru G, Lee D, Tlusty T, Pak H 2018 Phys. Rev. Lett. 120 020601
Google Scholar
[8] Dong H, Xu D Z, Cai C Y, Sun C P 2011 Phys. Rev. E 83 061108
Google Scholar
[9] Cai C Y, Dong H, Sun C P 2012 Phys. Rev. E 85 031114
Google Scholar
[10] Toyabe S, Sagawa T, Ueda M, Muneyuki E, Sano M 2010 Nat. Phys. 6 988
Google Scholar
[11] Lebedev A V, Lesovik G B, Vinokur V M, Blatter G 2018 Phys. Rev. B 98 214502
Google Scholar
[12] Naghiloo M, Alonso J J, Romito A, Lutz E, Murch K W 2018 Phys. Rev. Lett. 121 030604
Google Scholar
[13] Schaller G, Cerrillo J, Engelhardt G, Strasberg P 2018 Phys. Rev. B 97 195104
Google Scholar
[14] Jacobs K 2009 Phys. Rev. A 80 012322
Google Scholar
[15] Granger L, Kantz H 2011 Phys. Rev. E 84 061110
Google Scholar
[16] Sagawa T, Ueda M 2008 Phys. Rev. Lett. 100 080403
Google Scholar
[17] Koch-Janusz M, Ringel Z 2018 Nat. Phys. 14 578
Google Scholar
[18] Mehta P, Lang A H, Schwab D J 2016 J. Stat. Phys. 162 1153
Google Scholar
[19] Ito S, Sagawa T 2015 Nat. Commun. 6 7498
Google Scholar
[20] Barato A C, Hartich D, Seifert U 2014 New J. Phys. 16 103024
Google Scholar
[21] Mehta P, Schwab D J 2012 Proc. Natl. Acad. Sci. U.S.A. 109 17978
Google Scholar
[22] 李唯, 符婧, 杨贇贇, 何济洲 2019 68 220501
Google Scholar
Li W, Fu J, Yang Y Y, He J Z 2019 Acta Phys. Sin. 68 220501
Google Scholar
[23] 何弦, 何济洲, 肖宇玲 2012 61 150302
Google Scholar
He X, He J Z, Xiao Y L 2012 Acta Phys. Sin. 61 150302
Google Scholar
[24] Horowitz J M, Esposito M 2014 Phys. Rev. X 4 031015
[25] Barato A C, Hartich D, Seifert U 2014 New Journal of Physics 16 103024
[26] Yamamoto S, Ito S, Shiraishi N, Sagawa T 2016 Phys. Rev. E 94 052121
[27] Ptaszyński K, Esposito M 2019 Phys. Rev. Lett. 122 150603
Google Scholar
[28] Strasberg P, Schaller G, Brandes T, Esposito M 2017 Phys. Rev. X 7 021003
[29] Schnakenberg J 1976 Rev. Mod. Phys. 48 571
Google Scholar
[30] Breuer H P, Petruccione F 2001 The Theory of Open Quantum Systems (Oxford: Oxford University Press) pp110–149
[31] Schaller G 2014 Open Quantum Systems Far from Equilibrium (New York: Springer) pp73–74
[32] Spohn H 1978 J. Math. Phys. 19 1227
Google Scholar
[33] Esposito M, Harbola U, Mukamel S 2009 Rev. Mod. Phys. 81 1665
Google Scholar
[34] Thulasiraman K, Swamy M N S 1997 Graphs: Theory and Algorithms (New York: John Wiley & Sons) pp1–26
[35] Sagawa T, Ueda M 2013 New J. Phys. 15 125012
Google Scholar
[36] Bauer M, Abreu D, Seifert U 2012 J. Phys. A: Math. Theor. 45 162001
Google Scholar
[37] Ito S, Sagawa T 2013 Phys. Rev. Lett. 111 180603
Google Scholar
下载:
计量
- 文章访问数: 7232
- PDF下载量: 83
- 被引次数: 0
