-
以变截面含可穿透散射体波导为模型, 理论研究声波在非均匀波导中的最大透射问题. 通过耦合简正波理论构建模态域内透射矩阵和水平波数矩阵, 推导透射波能流的具体表达式, 分析任意入射波的能流透射率随频率的变化, 进而讨论任意给定频率下能够产生最大能流透射率的最佳入射波, 并给出数组全透射声场算例. 最佳入射波仅由可传播模态决定, 与衰逝模态无关. 利用衰逝模态不携带能流的特性, 讨论衰逝模态对产生能流最大透射声场的影响, 并分析最大能流透射的鲁棒性. 在频率满足一定条件时, 全透射声场可能表现出完美鲁棒性. 文中所述方法可延伸至多种非均匀波导以分析其中的能流最大透射问题.Inhomogeneity in a medium will cause wave scattering, influencing the transfer of energy or information. However, it is possible to prepare a prescribed wavefront which propagates through an inhomogeneous medium with unity flux-transmittance. This phenomenon is first predicted in the context of mesoscopic electron transport. Another remarkable phenomenon is the bimodal distribution of the transmission singular values, which implies that in a lossless medium the full solution space in the scattering region can be spanned only by open channels, which are completely transmitted, and closed channels, which are completely reflected. In mesoscopic physics, random-matrix theory is usually utilized to deal with the statistical properties of matrices with randomly distributed entries since the medium is assumed to be randomly fluctuating. In this paper, we propose a method of systematically studying the maximal flux transmission through an inhomogeneous acoustic waveguide. The model is chosen to be a waveguide with varying cross-sections and a penetrable scatterer, and the method is based on the coupled mode theory. This method can be used to analyze the frequency of nearly complete transmission for an arbitrary incident wave, and to analyze the incident wave that is able to generate the maximal flux-transmittance for any given frequency. We construct the transmission matrix and the horizontal wavenumber matrix by using orthonormal basis functions, and give the expression of flux-transmittance. Then the optimal incident wave which brings the maximal transmittance through the scattering region is derived based on singular value decomposition. The optimal incident waves are independent of the evanescent modes since evanescent modes do not transfer any energy. But the evanescent modes can give rise to the multivaluedness of wave solutions with complete flux transmission. Considering the fact that acoustic waveguides can naturally resist the influence of highly oscillating perturbations since most of them correspond to evanescent modes), the maximal flux transmission in waveguide is thus found to be highly robust. Especially at a specific frequency, the complete wave transmission has perfect robustness. This proposed method can be generalized to any other frequency, to other types of scatterers, or to other kinds of boundary conditions, and can provide guidance in designing acoustic metamaterials and in highly efficient communication.
-
Keywords:
- inhomogeneous waveguides /
- maximal flux transmission /
- complete wave transmission /
- optimal incident wave
[1] Dorokhov O 1982 Solid State Commun. 44 915
Google Scholar
[2] Dorokhov O 1984 Solid State Commun. 51 381
Google Scholar
[3] Imry Y 1986 Europhys. Lett. 1 249
Google Scholar
[4] Pendry J B, MacKinnon A, Pretre A B 1990 Physica A 168 400
Google Scholar
[5] Mello P A, Pereyra P, Kumar N 1988 Ann. Phys. 181 290
Google Scholar
[6] Nazarov Y V 1994 Phys. Rev. Lett. 73 134
Google Scholar
[7] Beenakker C W J 1997 Rev. Mod. Phys. 69 731
Google Scholar
[8] Vellekoop I M, Lagendijk A, Mosk A P 2010 Nat. Photonics 4 320
Google Scholar
[9] Popoff S M, Lerosey G, Carminati R, Fink M, Boccara A C, Gigan S 2010 Phys. Rev. Lett. 104 100601
Google Scholar
[10] Vellekoop I M, Mosk A P 2008 Phys. Rev. Lett. 101 120601
Google Scholar
[11] Choi W, Mosk A P, Park Q H, Choi W 2011 Phys. Rev. B 83 134207
Google Scholar
[12] Kim M, Choi Y, Yoon C, Choi W, Kim J, Park Q H, Choi W 2012 Nat. Photonics 6 581
Google Scholar
[13] Popoff S M, Goetschy A, Liew S F, Stone A D, Cao H 2014 Phys. Rev. Lett. 112 133903
Google Scholar
[14] Hao X, Martin-Rouault L, Cui M 2014 Sci. Rep. 4 5874
[15] Gérardin B, Laurent J, Derode A, Prada C, Aubry A 2014 Phys. Rev. Lett. 113 173901
Google Scholar
[16] Liew S F, Popoff S M, Mosk A P, Vos W L, Cao H 2014 Phys. Rev. B 89 224202
Google Scholar
[17] Liew S F, Cao H 2015 Opt. Express 23 11043
Google Scholar
[18] Yamilov A, Petrenko S, Sarma R, Cao H 2016 Phys. Rev. B 93 100201
Google Scholar
[19] Wang Z, Chong Y D, Joannopoulos J D, Soljačić M 2009 Nature 461 772
Google Scholar
[20] Lu L, Joannopoulos J D, Soljačić M 2014 Nat. Photonics 8 821
Google Scholar
[21] Rahm M, Cummer S A, Schurig D, Pendry J B, Smith D R 2008 Phys. Rev. Lett. 100 063903
Google Scholar
[22] Yu N F, Capasso F 2013 Nat. Mater. 13 139
[23] Asadchy V S, Faniayeu I A, Ra’di Y, Khakhomov S A, Semchenko I V, Tretyakov S A 2015 Phys. Rev. X 5 031005
[24] Bonnet-Ben Dhia A S, Nazarov S A 2013 Acoust. Phys. 59 633
Google Scholar
[25] Bonnet-Ben Dhia A S, Chesnel L, Nazarov S A 2015 Inverse Prob. 31 045006
Google Scholar
[26] Bonnet-Ben Dhia A S, Lunéville E, Mbeutcha Y, Nazarov S A 2017 Math. Methods Appl. Sci. 40 335
Google Scholar
[27] Bonnet-Ben Dhia A S, Chesnel L, Nazarov S A 2018 J. Math. Pures Appl. 111 79
Google Scholar
[28] Derode A, Roux P, Fink M 1995 Phys. Rev. Lett. 75 4206
Google Scholar
[29] Fink M, Cassereau D, Derode A, Prada C, Roux P, Tanter M, Thomas J L, Wu F 2000 Rep. Prog. Phys. 63 1933
Google Scholar
[30] Lerosey G, Rosny J, Tourin A, Fink M 2007 Science 315 1120
Google Scholar
[31] Mosk A P, Lagendijk A, Lerosey G, Fink M 2012 Nat. Photonics 6 283
Google Scholar
[32] Ma F Y, Huang M, Xu Y C, Wu J H 2018 Sci. Rep. 8 5906
Google Scholar
[33] Chen J, Xiao J, Lisevych D, Shakouri A, Fan Z 2018 Nat. Commun. 9 4920
Google Scholar
[34] Li Y, Assouar B M 2016 Appl. Phys. Lett. 108 063502
Google Scholar
[35] Shen C, Cummer S A 2018 Phys. Rev. Appl. 9 054009
Google Scholar
[36] Maurel A, Mercier J F, Félix S 2014 J. Acoust. Soc. Am. 135 165
Google Scholar
[37] 刘娟, 李琪 2021 70 064301
Google Scholar
Liu J, Li Q 2021 Acta Phys. Sin. 70 064301
Google Scholar
[38] Lu Y Y, McLaughlin J R 1996 J. Acoust. Soc. Am. 100 1432
Google Scholar
[39] Lu Y Y 2005 J. Comput. Appl. Math. 173 247
Google Scholar
[40] Pagneux V 2010 J. Comput. Appl. Math. 234 1834
Google Scholar
[41] Bonnet-Ben Dhia A S, Chesnel L, Pagneux V 2018 Proc. R. Soc. London, Ser. A 474 20180050
[42] Chéron É, Félix S, Pagneux V 2019 Phys. Rev. Lett. 122 125501
Google Scholar
[43] Guo W, Liu J, Bi W P, Aurégan Y, Pagneux V 2020 arXiv 2010.03646
[44] Pagneux V, Maurel A 2002 P. Roc. Soc. A-Math. Phys. 458 1913
Google Scholar
[45] Li Q, Liu J, Guo W 2019 Chin. Phys. B 29 014303
[46] Pagneux V, Maurel A 2006 Proc. R. Soc. A- Math. Phys. 462 1315
[47] 郭威, 杨德森 2020 69 074301
Google Scholar
Guo W, Yang D S 2020 Acta Phys. Sin. 69 074301
Google Scholar
-
图 1 变截面含散射体非均匀波导示意图
Fig. 1. Configuration of the inhomogeneous waveguide with varying cross-sections and one scatterer.
图 2 平面波能流透射率随频率变化曲线
Fig. 2. Energy flux transmittance as a function of frequency when injecting a plane wave.
图 3 (a) 平面波能流全透射声场(
$k = 0.95{\text{π}} $ ); (b) 平面波能流零透射声场($k = 0.735{\text{π}} $ )Fig. 3. (a) Wave field with unity energy flux transmittance generated by a plane wave (
$k = 0.95{\text{π}} $ ); (b) wave field with zero energy flux transmittance generated by a plane wave ($k = 0.735{\text{π}} $ ).
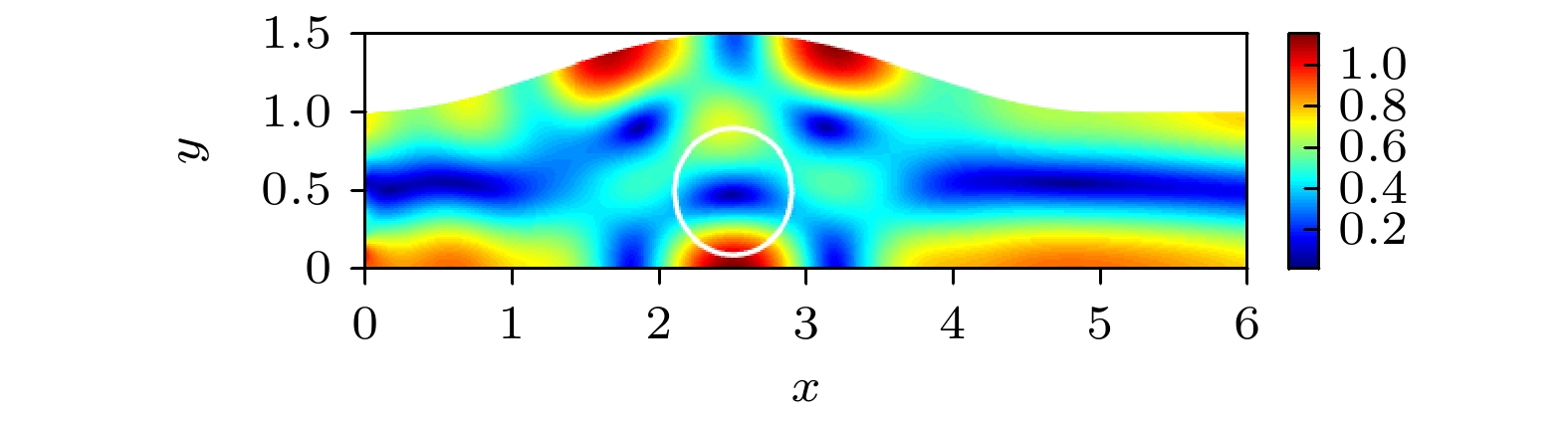
图 4 (a) Comsol计算平面波能流全透射声场(
$f = 712$ Hz); (b) Comsol计算平面波能流零透射声场($f = 551$ Hz)Fig. 4. (a) Wave field calculated by Comsol with unity energy flux transmittance generated by a plane wave (
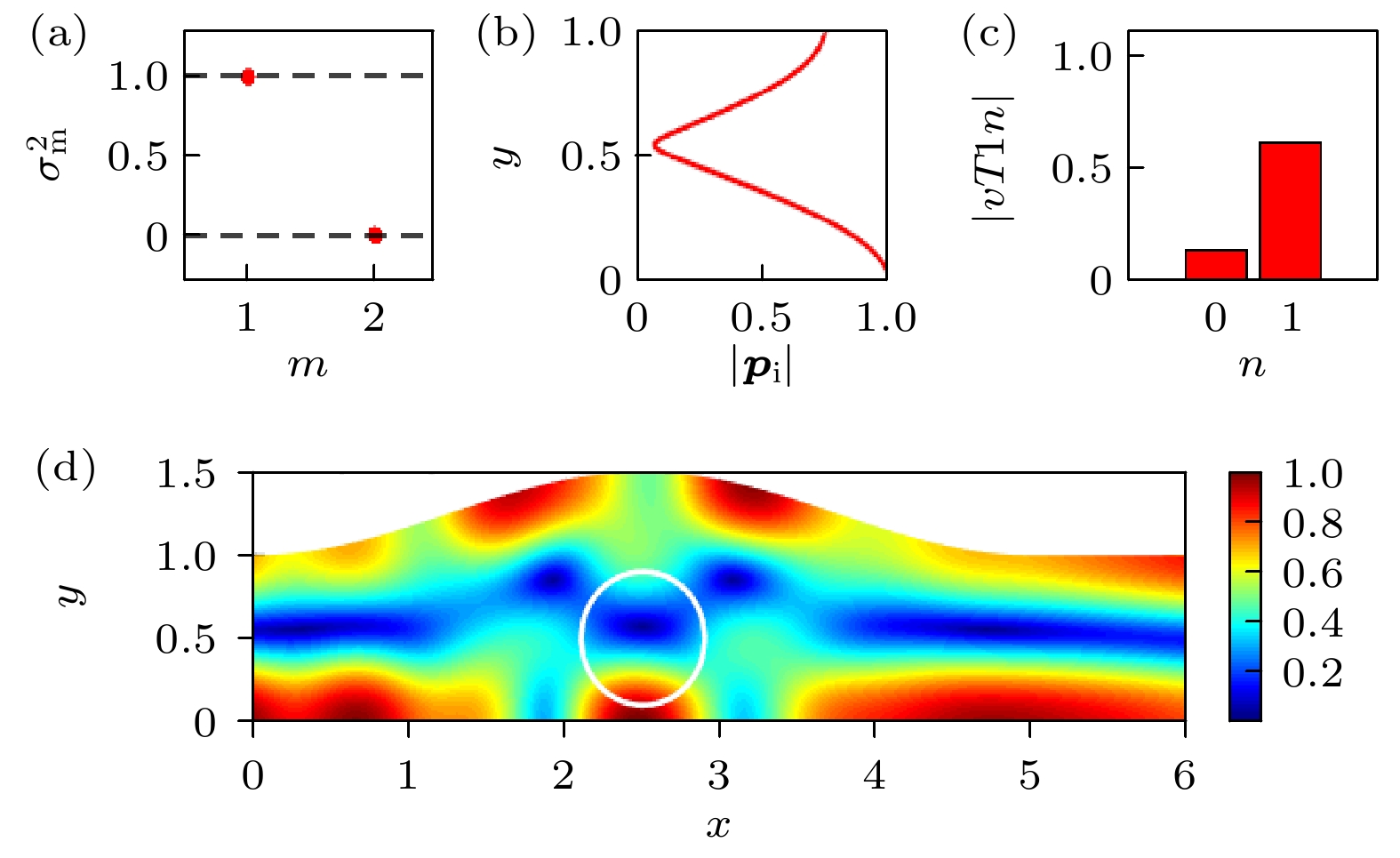
$f = $ $ 712$ Hz); (b) wave field calculated by Comsol with zero energy flux transmittance generated by a plane wave ($f = $ $ 551$ Hz).
图 5 (a) 奇异值平方分布; (b) 最佳入射波幅值分布; (c) 最佳入射波的模态展开系数; (d) 产生能流最大透射的声场. 波导参数与图2中使用的一致, 频率
$k = 1.45{\text{π}} $ Fig. 5. (a) Distribution of squares of singular values; (b) modulus of the optimal incident wave; (c) expansion coefficients of the optimal incident wave; (d) wave field with the maximum energy flux transmittance. The geometry of the waveguide is same as that in Fig. 2, and the frequency is
$k = 1.45{\text{π}} $ .
图 7 最佳入射波存在随机扰动时的声场
Fig. 7. Wave field generated by a disturbed optimal incident wave.
图 8 最佳入射波存在随机干扰时能流透射率的 (a)期望和(b)相对标准差随频率的变化
Fig. 8. (a) Expectation and (b) relative standard deviation of the flux-transmittance when the optimal incident wave is randomly perturbed.
-
[1] Dorokhov O 1982 Solid State Commun. 44 915
Google Scholar
[2] Dorokhov O 1984 Solid State Commun. 51 381
Google Scholar
[3] Imry Y 1986 Europhys. Lett. 1 249
Google Scholar
[4] Pendry J B, MacKinnon A, Pretre A B 1990 Physica A 168 400
Google Scholar
[5] Mello P A, Pereyra P, Kumar N 1988 Ann. Phys. 181 290
Google Scholar
[6] Nazarov Y V 1994 Phys. Rev. Lett. 73 134
Google Scholar
[7] Beenakker C W J 1997 Rev. Mod. Phys. 69 731
Google Scholar
[8] Vellekoop I M, Lagendijk A, Mosk A P 2010 Nat. Photonics 4 320
Google Scholar
[9] Popoff S M, Lerosey G, Carminati R, Fink M, Boccara A C, Gigan S 2010 Phys. Rev. Lett. 104 100601
Google Scholar
[10] Vellekoop I M, Mosk A P 2008 Phys. Rev. Lett. 101 120601
Google Scholar
[11] Choi W, Mosk A P, Park Q H, Choi W 2011 Phys. Rev. B 83 134207
Google Scholar
[12] Kim M, Choi Y, Yoon C, Choi W, Kim J, Park Q H, Choi W 2012 Nat. Photonics 6 581
Google Scholar
[13] Popoff S M, Goetschy A, Liew S F, Stone A D, Cao H 2014 Phys. Rev. Lett. 112 133903
Google Scholar
[14] Hao X, Martin-Rouault L, Cui M 2014 Sci. Rep. 4 5874
[15] Gérardin B, Laurent J, Derode A, Prada C, Aubry A 2014 Phys. Rev. Lett. 113 173901
Google Scholar
[16] Liew S F, Popoff S M, Mosk A P, Vos W L, Cao H 2014 Phys. Rev. B 89 224202
Google Scholar
[17] Liew S F, Cao H 2015 Opt. Express 23 11043
Google Scholar
[18] Yamilov A, Petrenko S, Sarma R, Cao H 2016 Phys. Rev. B 93 100201
Google Scholar
[19] Wang Z, Chong Y D, Joannopoulos J D, Soljačić M 2009 Nature 461 772
Google Scholar
[20] Lu L, Joannopoulos J D, Soljačić M 2014 Nat. Photonics 8 821
Google Scholar
[21] Rahm M, Cummer S A, Schurig D, Pendry J B, Smith D R 2008 Phys. Rev. Lett. 100 063903
Google Scholar
[22] Yu N F, Capasso F 2013 Nat. Mater. 13 139
[23] Asadchy V S, Faniayeu I A, Ra’di Y, Khakhomov S A, Semchenko I V, Tretyakov S A 2015 Phys. Rev. X 5 031005
[24] Bonnet-Ben Dhia A S, Nazarov S A 2013 Acoust. Phys. 59 633
Google Scholar
[25] Bonnet-Ben Dhia A S, Chesnel L, Nazarov S A 2015 Inverse Prob. 31 045006
Google Scholar
[26] Bonnet-Ben Dhia A S, Lunéville E, Mbeutcha Y, Nazarov S A 2017 Math. Methods Appl. Sci. 40 335
Google Scholar
[27] Bonnet-Ben Dhia A S, Chesnel L, Nazarov S A 2018 J. Math. Pures Appl. 111 79
Google Scholar
[28] Derode A, Roux P, Fink M 1995 Phys. Rev. Lett. 75 4206
Google Scholar
[29] Fink M, Cassereau D, Derode A, Prada C, Roux P, Tanter M, Thomas J L, Wu F 2000 Rep. Prog. Phys. 63 1933
Google Scholar
[30] Lerosey G, Rosny J, Tourin A, Fink M 2007 Science 315 1120
Google Scholar
[31] Mosk A P, Lagendijk A, Lerosey G, Fink M 2012 Nat. Photonics 6 283
Google Scholar
[32] Ma F Y, Huang M, Xu Y C, Wu J H 2018 Sci. Rep. 8 5906
Google Scholar
[33] Chen J, Xiao J, Lisevych D, Shakouri A, Fan Z 2018 Nat. Commun. 9 4920
Google Scholar
[34] Li Y, Assouar B M 2016 Appl. Phys. Lett. 108 063502
Google Scholar
[35] Shen C, Cummer S A 2018 Phys. Rev. Appl. 9 054009
Google Scholar
[36] Maurel A, Mercier J F, Félix S 2014 J. Acoust. Soc. Am. 135 165
Google Scholar
[37] 刘娟, 李琪 2021 70 064301
Google Scholar
Liu J, Li Q 2021 Acta Phys. Sin. 70 064301
Google Scholar
[38] Lu Y Y, McLaughlin J R 1996 J. Acoust. Soc. Am. 100 1432
Google Scholar
[39] Lu Y Y 2005 J. Comput. Appl. Math. 173 247
Google Scholar
[40] Pagneux V 2010 J. Comput. Appl. Math. 234 1834
Google Scholar
[41] Bonnet-Ben Dhia A S, Chesnel L, Pagneux V 2018 Proc. R. Soc. London, Ser. A 474 20180050
[42] Chéron É, Félix S, Pagneux V 2019 Phys. Rev. Lett. 122 125501
Google Scholar
[43] Guo W, Liu J, Bi W P, Aurégan Y, Pagneux V 2020 arXiv 2010.03646
[44] Pagneux V, Maurel A 2002 P. Roc. Soc. A-Math. Phys. 458 1913
Google Scholar
[45] Li Q, Liu J, Guo W 2019 Chin. Phys. B 29 014303
[46] Pagneux V, Maurel A 2006 Proc. R. Soc. A- Math. Phys. 462 1315
[47] 郭威, 杨德森 2020 69 074301
Google Scholar
Guo W, Yang D S 2020 Acta Phys. Sin. 69 074301
Google Scholar
下载:
计量
- 文章访问数: 4020
- PDF下载量: 58
- 被引次数: 0
