-
根据广义相对论, 弱场近似条件下引力场中不仅含有经典的牛顿引力场, 还存在一种类比于磁场概念的引力“磁”场, 引力磁场的命名借用了电动力学中磁场的概念. 为了研究引力磁场的物理性质和它引发的一些关联效应, 本文首先从线性爱因斯坦方程出发, 利用相似变换的方法从方程的二级张量场中分解出了引力的“磁”分量并定义了引力磁场; 在此基础上考虑了一种通有匀速流体的环状微管模型, 通过电动力学的分析方法研究了远离微管区域的引力磁场分布特征, 重点在计算过程中改进了以往对这类环状模型引力磁场的计算方法, 表明了这类模型的引力磁场远场分布模式与磁偶极子磁场的远场分布类似; 之后利用类磁场的性质研究了引力磁场的动力学特征, 首次研究了测试粒子在线性时变引力磁场及余弦时变引力磁场中的运动规律, 同时通过设计一种具有双层结构且通有加速流动流体的环状微管模型改进了前人对时变引力磁场中引力感应、惯性系拖曳现象的研究办法, 从更清晰的角度用更简单的数学通过引力电磁理论研究和展示了引力感应现象和广义相对论中的惯性系拖曳现象. 全文为引力磁场及其关联效应的研究提供了一些新的方法和思路.According to the General Relativity (GR), under the approximation of the weak field, the weak gravitational field not only contains the classical Newtonian gravitational field, but also contains a gravitomagnetic (GM) field analogous to the concept of magnetic field, and the name of GM field borrows the basic idea of the magnetic field in electrodynamics. In order to study the physical properties of GM field and its associated effects, firstly, we use a similarity transformation method to decompose the gravitomagnetic component from the second-order tensor field in linearized Einstein field equation and define the concept of the GM field. Then, on this basis, we consider a circular microtube model with uniform velocity fluids (or superfluids), and study the distribution characteristics of the far GM field by this special model. We use a simpler approximation approach to improve the previous calculation method of the GM field in these kind of rings model, the result shows that the distribution characteristic of the far GM field in this model is analogous to the magnetic field produced by a dipole, it is a good correspondence between this microtube model and the dipole model. After that, we have studied the dynamic characteristics of GM field by analogizing the properties of magnetic field, and studied the test particles’ tracks in the linear time-varying GM field and the cosine time-varying GM field in the first time. In addition, in order to improve the previous research methods of ‘gravitational induction’ and ‘frame dragging’ in the GR, we have designed a circular microtube model which has a double-layer structure and with the accelerating flow fluid (or superfluids), we use simpler mathematics than before to explain these two effects by this special model. In conclusion, this work provides some new methods for the study of GM field and its associated effects.
-
Keywords:
- linearized theory of gravity /
- circular microtube model /
- gravitomagnetic field /
- gravitomagnetism
[1] Rocha F, Malheiro M, Marinho Jr R 2015 Proceedings of the MG14 Meeting on General Relativity Rome, Italy, July 12−18, 2015 p4331
[2] Ruggiero M L 2016 Astrophys. Space Sci. 361 140
Google Scholar
[3] Tajmar M, Assis A K T 2015 Can. J. Phys. 93 1571
Google Scholar
[4] Everitt C W F, DeBra D B, Parkinson B W, Turneaure J P, Conklin J W, Heifetz M I, Keiser G M, Silbergleit A S, Holmes T, Kolodziejczak J, Al-Meshari M, Mester J C, Muhlfelder B, Solomonik V G, Stahl K, Worden P W, Jr Bencze W, Buchman S, Clarke B, Al-Jadaan A, Al-Jibreen H, Li J, Lipa J A, Lockhart J M, Al-Suwaidan B, Taber M, Wang S 2011 Phys. Rev. Lett. 106 221101
Google Scholar
[5] Ciufolini I, Pavlis E C 2004 Nature 431 958
Google Scholar
[6] Iorio L 2006 Classical Quantum Gravity 23 5451
Google Scholar
[7] Iorio L 2012 Sol. Phys. 281 815
Google Scholar
[8] Tajmar M, Plesescu F, Seifert B, Marhold K 2007 AIP Conf. Proc. 880 1071
Google Scholar
[9] Mashhoon B, Iorio L, Lichtenegger H 2001 Phys. Lett. A 292 49
Google Scholar
[10] Ruggiero M L 2015 Int. J. Mod. Phys. D 24 1550060
[11] Bini D, Cherubini C, Chicone C, Mashhoon B 2008 Classical Quantum Gravity 25 225014
Google Scholar
[12] Tartaglia A, Ruggiero M L 2003 Eur. J. Phys. 25 203
Google Scholar
[13] Ruggiero M L, Tartaglia A 2002 arXiv: 0207065 [gr-qc]
[14] Wu N 2005 Commun. Theor. Phys. 44 883
Google Scholar
[15] Vető B 2011 Eur. J. Phys 32 1323
Google Scholar
[16] Mashhoon B 2008 Classical Quantum Gravity 25 085014
Google Scholar
[17] 刘辽, 赵峥 2004 广义相对论 (北京: 高等教育出版社) 第80—90页
Liu L, Zhao Z 2004 General Relativity (Beijing: Higher Education Press) pp80–90 (in Chinese)
[18] Mironov V L, Mironov S V 2014 J. Mod. Phys. 5 917
Google Scholar
[19] Demir S 2013 Int. J. Theor. Phys. 52 105
Google Scholar
[20] Mashhoon B 2003 arXiv: 0311030 [gr-qc]
[21] Clark S 2006 New Sci. 192 36
[22] De Matos C J, Tajmar M 2005 Physica C 432 167
Google Scholar
[23] Aharonov Y, Carmi G 1973 Found. Phys. 3 493
Google Scholar
[24] Overhauser A W, Colella R 1974 Phys. Rev. Lett. 33 1237
Google Scholar
[25] Arif M, Dewey M S, Greene G L, Jocobson D, Werner S 1994 Phys. Lett. A 184 154
Google Scholar
[26] Krishnan V V, Bailes M, Van Straten W, Wex W, Ferire P C C, Keane E F, Tauris T M, Rosado P A, Bhat N D R, Flynn C, Jameson A, Ostowski S 2020 Science 367 577
Google Scholar
[27] Tajmar M, De Matos C J 2003 Physica C 385 551
Google Scholar
[28] 王刚志, 郭肖勇, 吴泽华, 王晋研, 夏梦莹 2018 物理与工程 28 84
Google Scholar
Wang G Z, Guo X Y, Wu Z H, Wang J Y, Xia M Y 2018 Physics and Engineering 28 84
Google Scholar
[29] Shen J Q 2002 Gen. Relativ. Gravition 34 1423
Google Scholar
[30] Mashhoon B, Gronwald F, Theiss D S 1999 Ann. Phys. 8 135
Google Scholar
[31] Braginsky V B, Caves C M, Thorne K S 1977 Phys. Rev. D 15 2047
Google Scholar
[32] 梁灿彬, 曹周键, 陈陟陶 2018 电磁学 (拓展篇) (北京: 高等教育出版社) 第222−227页
Liang C B, Cao Z J, Chen Z T 2018 Electromagnetics (Extended) (Beijing: Higher Education Press) pp222−227 (in Chinese)
-
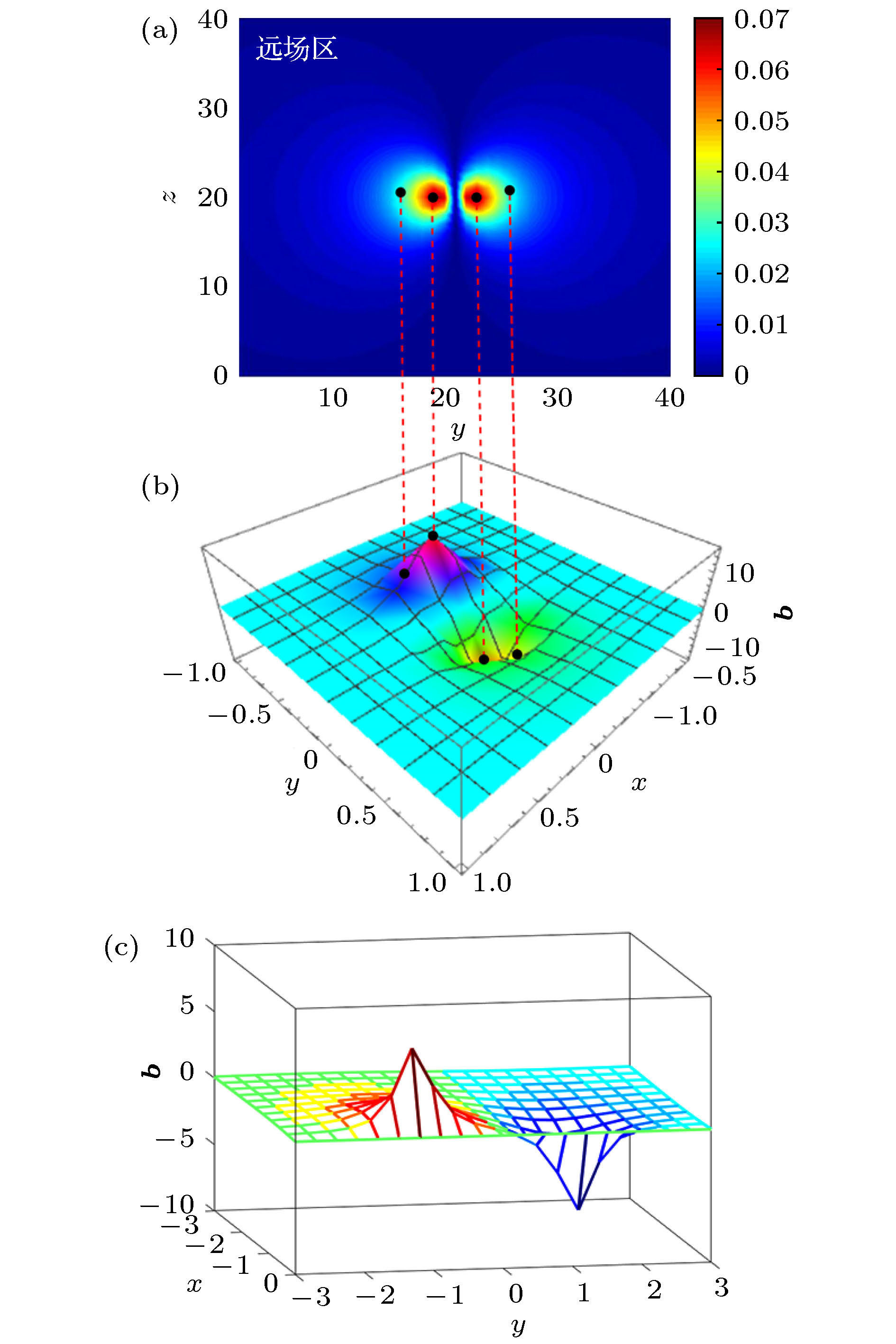
图 2 微管模型引力磁场远场分布特征 (a) 微管模型y-z平面沿y方向的引力磁场分布色谱图; (b) 微管模型x-y平面沿y方向的引力磁场强度分布特征图; (c) 微管模型x-y平面沿y方向上引力磁场强度随y坐标轴的变化曲线
Fig. 2. The far-field distribution of GM field in the microtube model: (a) The intensity plots of GM field's along y-direction in y-z plane of microtube model; (b) the distribution of GM field's along y-direction in x-y plane of microtube model; (c) the b-y function along y-direction in x-y plane of microtube model.
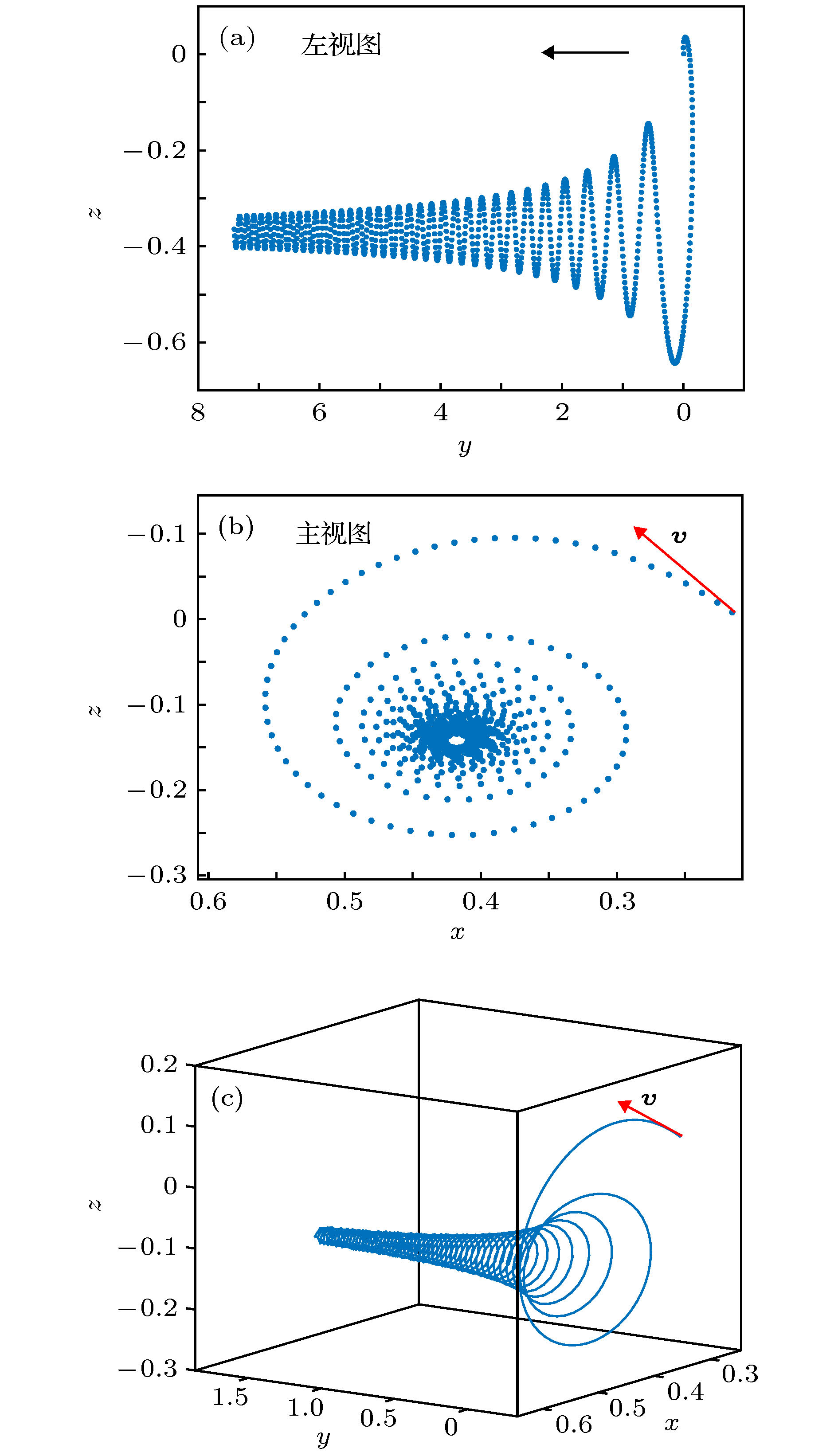
图 3 模式一下测试粒子的运动轨迹 (a) 测试粒子在线性时变引力磁场中运动轨迹的左视图; (b) 测试粒子在线性时变引力磁场中运动轨迹的主视图; (c) 测试粒子在线性时变引力磁场中的全空间运动轨迹
Fig. 3. The test-particle's track in linear time-varying GM field: (a) The left view of the test-particle's track; (b) the main view of the test-particle's track; (c) the test-particle's track in the whole space.
图 4 模式二下测试粒子的运动轨迹 (a) 测试粒子在余弦时变引力磁场中运动轨迹的俯视图; (b) 测试粒子在余弦时变引力磁场中运动轨迹的左视图; (c) 测试粒子在余弦时变引力磁场中的全空间运动轨迹
Fig. 4. The test-particle's track in cosine time-varying GM field: (a) The top view of the test-particle's track; (b) the left view of the test-particle's track; (c) the test-particle's track in the whole space.
图 5 用于研究引力感应效应的旋转球壳模型
Fig. 5. The rotating spherical shell model for studying the gravitational induction effect.
图 6 基于微管模型的引力感应演示模型
Fig. 6. The demonstration model for studying gravitational induction based on the microtube model.
图 7 流体参数设定及涡旋场的仿真 (a) 流体含时角动量的线性函数; (b) 环2所在平面内激发的涡旋引力电场的强度色谱图; (c) 环2内流体的受力区域
Fig. 7. The parameter description of fluid and the vortex field’s simulation: (a) The linear function between the angular momentum L and time; (b) the distribution of vortex field in the z = 0 plane which produced by the ring 2; (c) the fluid’s stressed region in the plane of the ring 2.
-
[1] Rocha F, Malheiro M, Marinho Jr R 2015 Proceedings of the MG14 Meeting on General Relativity Rome, Italy, July 12−18, 2015 p4331
[2] Ruggiero M L 2016 Astrophys. Space Sci. 361 140
Google Scholar
[3] Tajmar M, Assis A K T 2015 Can. J. Phys. 93 1571
Google Scholar
[4] Everitt C W F, DeBra D B, Parkinson B W, Turneaure J P, Conklin J W, Heifetz M I, Keiser G M, Silbergleit A S, Holmes T, Kolodziejczak J, Al-Meshari M, Mester J C, Muhlfelder B, Solomonik V G, Stahl K, Worden P W, Jr Bencze W, Buchman S, Clarke B, Al-Jadaan A, Al-Jibreen H, Li J, Lipa J A, Lockhart J M, Al-Suwaidan B, Taber M, Wang S 2011 Phys. Rev. Lett. 106 221101
Google Scholar
[5] Ciufolini I, Pavlis E C 2004 Nature 431 958
Google Scholar
[6] Iorio L 2006 Classical Quantum Gravity 23 5451
Google Scholar
[7] Iorio L 2012 Sol. Phys. 281 815
Google Scholar
[8] Tajmar M, Plesescu F, Seifert B, Marhold K 2007 AIP Conf. Proc. 880 1071
Google Scholar
[9] Mashhoon B, Iorio L, Lichtenegger H 2001 Phys. Lett. A 292 49
Google Scholar
[10] Ruggiero M L 2015 Int. J. Mod. Phys. D 24 1550060
[11] Bini D, Cherubini C, Chicone C, Mashhoon B 2008 Classical Quantum Gravity 25 225014
Google Scholar
[12] Tartaglia A, Ruggiero M L 2003 Eur. J. Phys. 25 203
Google Scholar
[13] Ruggiero M L, Tartaglia A 2002 arXiv: 0207065 [gr-qc]
[14] Wu N 2005 Commun. Theor. Phys. 44 883
Google Scholar
[15] Vető B 2011 Eur. J. Phys 32 1323
Google Scholar
[16] Mashhoon B 2008 Classical Quantum Gravity 25 085014
Google Scholar
[17] 刘辽, 赵峥 2004 广义相对论 (北京: 高等教育出版社) 第80—90页
Liu L, Zhao Z 2004 General Relativity (Beijing: Higher Education Press) pp80–90 (in Chinese)
[18] Mironov V L, Mironov S V 2014 J. Mod. Phys. 5 917
Google Scholar
[19] Demir S 2013 Int. J. Theor. Phys. 52 105
Google Scholar
[20] Mashhoon B 2003 arXiv: 0311030 [gr-qc]
[21] Clark S 2006 New Sci. 192 36
[22] De Matos C J, Tajmar M 2005 Physica C 432 167
Google Scholar
[23] Aharonov Y, Carmi G 1973 Found. Phys. 3 493
Google Scholar
[24] Overhauser A W, Colella R 1974 Phys. Rev. Lett. 33 1237
Google Scholar
[25] Arif M, Dewey M S, Greene G L, Jocobson D, Werner S 1994 Phys. Lett. A 184 154
Google Scholar
[26] Krishnan V V, Bailes M, Van Straten W, Wex W, Ferire P C C, Keane E F, Tauris T M, Rosado P A, Bhat N D R, Flynn C, Jameson A, Ostowski S 2020 Science 367 577
Google Scholar
[27] Tajmar M, De Matos C J 2003 Physica C 385 551
Google Scholar
[28] 王刚志, 郭肖勇, 吴泽华, 王晋研, 夏梦莹 2018 物理与工程 28 84
Google Scholar
Wang G Z, Guo X Y, Wu Z H, Wang J Y, Xia M Y 2018 Physics and Engineering 28 84
Google Scholar
[29] Shen J Q 2002 Gen. Relativ. Gravition 34 1423
Google Scholar
[30] Mashhoon B, Gronwald F, Theiss D S 1999 Ann. Phys. 8 135
Google Scholar
[31] Braginsky V B, Caves C M, Thorne K S 1977 Phys. Rev. D 15 2047
Google Scholar
[32] 梁灿彬, 曹周键, 陈陟陶 2018 电磁学 (拓展篇) (北京: 高等教育出版社) 第222−227页
Liang C B, Cao Z J, Chen Z T 2018 Electromagnetics (Extended) (Beijing: Higher Education Press) pp222−227 (in Chinese)
下载:
计量
- 文章访问数: 10182
- PDF下载量: 103
- 被引次数: 0
