-
基于非平衡格林函数方法, 理论研究了Z轴方向局域交换场和电场对锗烯纳米带中电子自旋极化输运性质的影响. 结果表明对锗烯的边缘区域施加强度大于其2倍有效自旋轨道耦合强度的交换场, 可使自旋向上和向下电子的能带在不同的能量区间产生带隙, 从而实现对不同自旋取向电子的100%过滤. 提出了一种利用电场辅助降低自旋过滤效应所需阈值交换场强度的方法. 研究表明, 同时对中心器件区域施加局域交换场和电场, 可以在小于有效自旋轨道耦合的弱交换场强度下, 在较大的能量窗口区域过滤自旋向上或向下的电子. 增大局域交换场强度, 自旋过滤效应所对应的能量区间显著增大.Germanene, which has been synthesized recently, is a single-layered material composed of germanium atoms. Almost all the striking properties of graphene can be transferred to germanene, because both of them have the same honeycomb lattice structure. In contrast with graphene, germanene has a sizable band gap and spin dependent helical edge states, which make it attractive candidate for spintronic applications. By using the nonequilibrium Green’s function method, the effects of Z-axis local exchange field and electric field on spin-polarized transport properties in germanene nanoribbon are studied theoretically. The results reveal that by exerting an exchange field with a strength greater than twice the effective spin-orbit coupling to the edge region of germanene, the spin resolved band gaps can be generated in different energy ranges, and thus 100% filtering of spin-up or spin-down electrons can be achieved. We theoretically propose a method to reduce the threshold exchange field strength for the spin filter effect by using the electric field. The results show that the spin-filter effect can be achieved in a larger energy range under a weaker exchange field when the electric field are applied to the entire central device region. With the increase of the local exchange field intensity, the energy range corresponding to the spin filter effect will increase significantly.
-
Keywords:
- germanene /
- local exchange field /
- spin-filter effect
[1] Geim A K, Novoselov K S 2006 Nat. Mater. 6 183
[2] Neto A H C, Guinea F, Peres N M R, Novoselov K S, Geim A K 2009 Rev. Mod. Phys. 81 109
 Google Scholar
Google Scholar
[3] Takeda K, Shiraishi K 1994 Phys. Rev. B 50 14916
 Google Scholar
Google Scholar
[4] Cahangirov S, Topsakal M, Akturk E, Sahin H, Ciraci S 2009 Phys. Rev. Lett. 102 236804
 Google Scholar
Google Scholar
[5] Liu C C, W X Feng W X, Yao Y G 2011 Phys. Rev. Lett. 107 076802
 Google Scholar
Google Scholar
[6] Seixas L, Padilha J E, Fazzio A 2014 Phys. Rev. B 89 195403
 Google Scholar
Google Scholar
[7] 秦志辉 2017 66 216802
 Google Scholar
Google Scholar
Qin Z H 2017 Acta Phys. Sin. 66 216802
 Google Scholar
Google Scholar
[8] Vogt P, Padova P D, Quaresima C, Avila J, Frantzeskakis E, Asensio M C, Resta A, Ealet A, Lay G L 2012 Phys. Rev. Lett. 108 155501
 Google Scholar
Google Scholar
[9] Fleurence A, Friedlein R, Ozaki T, Kawai H, Wang Y, Takamura Y Y 2012 Phys. Rev. Lett. 108 245501
 Google Scholar
Google Scholar
[10] Meng L, Wang Y L, Zhang L Z, Du S X, Wu R T, Li L F, Zhang Y, Li G, Zhou H T, Hofer W A, Gao H J 2013 Nano Lett. 13 685
 Google Scholar
Google Scholar
[11] Chiappe D, Scalise E, Cinquanta E, Grazianetti C, van den Broek B, Fanciulli M, Houssa M, Molle A 2014 Adv. Mater. 26 2096
 Google Scholar
Google Scholar
[12] Li L F, Lu S Z, Pan J B, Qin Z H, Wang Y Q, Wang Y L, Cao G Y, Du S X, Gao H 2014 J. Adv. Mater. 26 4820
 Google Scholar
Google Scholar
[13] Davila M E, Xian L, Cahangirov S, Rubio A, Le Lay G 2014 New J. Phys. 16 095002
 Google Scholar
Google Scholar
[14] Derivaz M, Dentel D, Stephan R, Hanf M C, Mehdaoui A, Sonnet P, Pirri C 2015 Nano Lett. 15 2510
 Google Scholar
Google Scholar
[15] Zhu F F, Chen W J, Xu Y, Gao C L, Guan D D, Liu C H, Qian D, Zhang S C, Jia J 2015 Nat. Mater. 14 1020
 Google Scholar
Google Scholar
[16] Zhang L, Bampoulis P, Rudenko A N, Yao Q, Houselt A V, Poelsema B, Katsnelson M I, Zandvliet H J W 2016 Phys. Rev. Lett. 116 256804
 Google Scholar
Google Scholar
[17] Tabert C J, Nicol E J 2013 Phys. Rev. B 87 235426
 Google Scholar
Google Scholar
[18] Rachel S, Ezawa M 2014 Phys. Rev. B 89 195303
 Google Scholar
Google Scholar
[19] Saxena R, Saha A, Rao S 2015 Phys. Rev. B 92 245412
 Google Scholar
Google Scholar
[20] Liu D P, Yu Z M, Liu Y L 2016 Phys. Rev. B 94 155112
 Google Scholar
Google Scholar
[21] Tao L L, Cheung K T, Zhang L, Wang J 2017 Phys. Rev. B 95 121407
 Google Scholar
Google Scholar
[22] Tian H Y, Wang S K, Hu J G, Wang J 2015 J. Phys.: Condens. Matter 27 125005
 Google Scholar
Google Scholar
[23] Ren C, Zhou B, Sun M, Wang S, Li Y 2018 Appl. Phys. Express 11 063006
 Google Scholar
Google Scholar
[24] Szafran B, Mreńca-Kolasińska A, Rzeszotarski B 2018 Phys. Rev. B 97 165303
 Google Scholar
Google Scholar
[25] Zheng J, Chi F, Guo Y 2018 Phys. Rev. Appl. 9 024012
 Google Scholar
Google Scholar
[26] Zheng J, Chi F, Guo Y 2018 Appl. Phys. Lett. 113 112404
 Google Scholar
Google Scholar
[27] Luo M 2019 Phys. Rev. B 99 165407
 Google Scholar
Google Scholar
[28] Verma S, Kundu A 2019 Phys. Rev. B 99 121409
 Google Scholar
Google Scholar
[29] Ziese M, Thornton M J 2001 Spin Electronics (New York: Springer-Verlag) pp396−415
[30] Fert A 2008 Rev. Mod. Phys. 80 1517
 Google Scholar
Google Scholar
[31] 郭永, 顾秉林, 川添良幸 2000 49 1814
 Google Scholar
Google Scholar
Guo Y, Gu B L, Yoshiyuki K 2000 Acta Phys. Sin. 49 1814
 Google Scholar
Google Scholar
[32] Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802
 Google Scholar
Google Scholar
[33] Ezawa M 2012 Phys. Rev. Lett. 109 055502
 Google Scholar
Google Scholar
[34] Meir Y, Wingreen N S 1992 Phys. Rev. Lett. 68 2512
 Google Scholar
Google Scholar
[35] Lee D H, Joannopoulos J D 1981 Phys. Rev. B 23 4988
 Google Scholar
Google Scholar
[36] Lee D H, Joannopoulos J D 1981 Phys. Rev. B 23 4997
 Google Scholar
Google Scholar
-
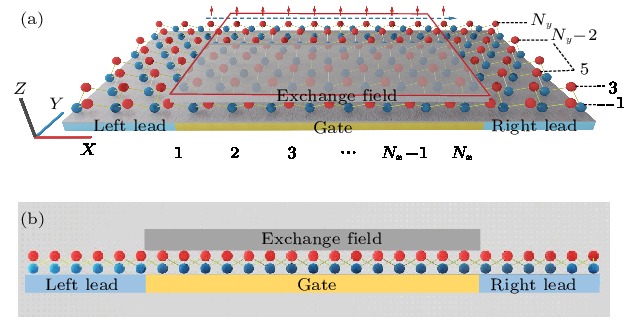
图 1 (a)单层锗烯自旋过滤器件结构示意图(左、右两侧蓝色区域为左、右电极区域; 中间红色实线包围区域内为中心器件区; 灰色和黄色分别表示Z轴方向交换场和电场的施加区域); (b)单层锗烯自旋过滤器件侧视图(红色和蓝色小球分别代表锗烯翘曲层顶部和底部的锗原子)
Fig. 1. (a) Schematic structure of of germanene spin filter. The blue regions on the left and right side are left and right lead. The area surrounded by red solid line is the central device. The regions shown in gray and yellow are exerted to the Z-direction exchange field and electric field. (b) Side view of germanene spin filter. Red and yellow spheres represent atoms in the top and bottom buckled-layer of germanene.
图 2 施加不同强度的局域交换场M时, 电导G与电子费米能量
$E_{\rm F}$ 之间的关系(红色实线表示自旋向上的电子, 蓝色虚线表示自旋向下的电子) (a) M = 0.01t, 0.03t, 0.05t, 0.07t时的自旋相关电导; (b) M = 0.09t时的自旋相关电导Fig. 2. Relationship between the conductance G and electron Fermi energy
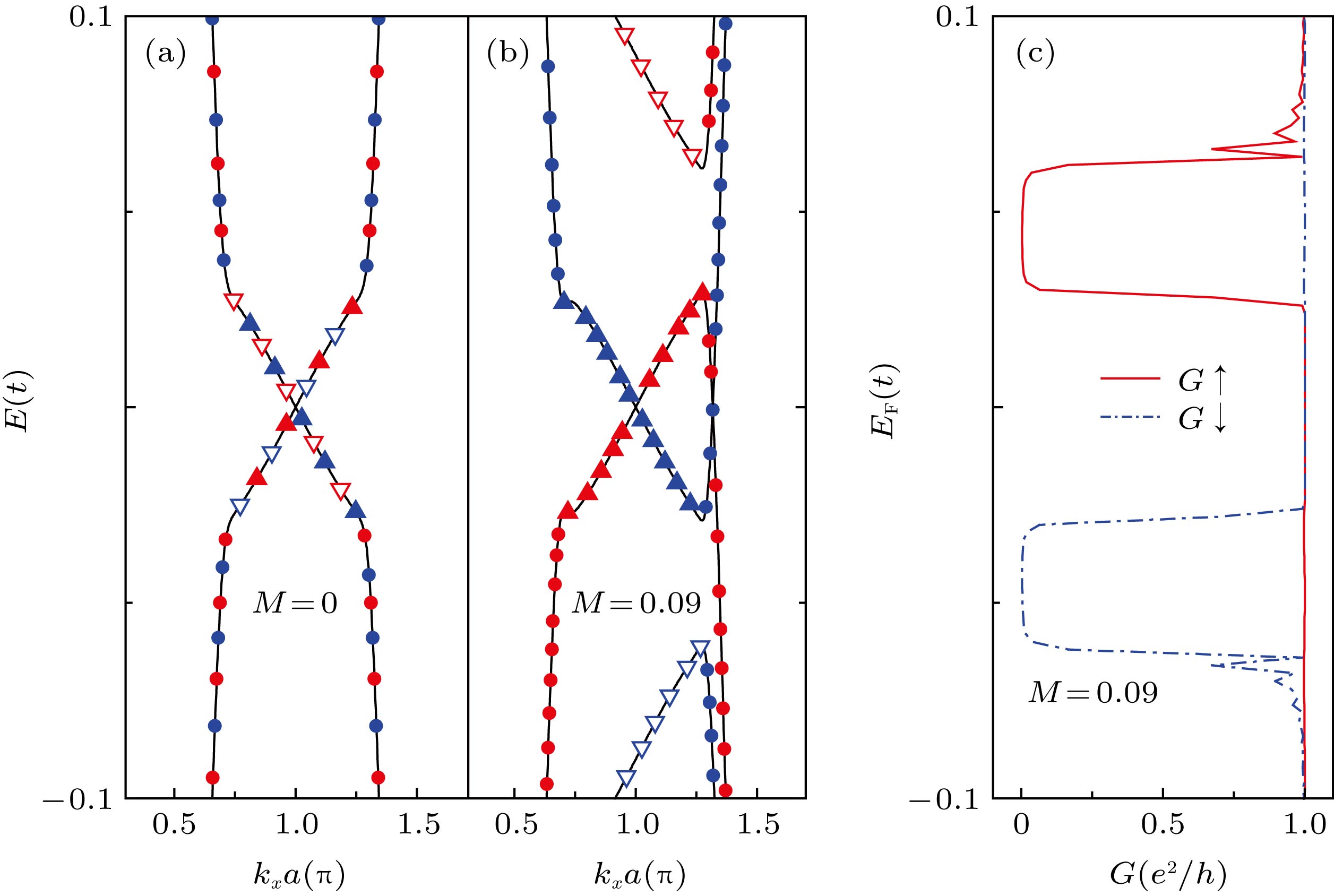
$E_{\rm F}$ when applying different values of local exchange field M: (a) Spin-dependent conductance with M = 0.01t, 0.03t, 0.05t, 0.07t; (b) spin-dependent conductance with M = 0.09t. The red solid line represents spin-up electrons and the blue dash line represents spin-down electrons.图 3 (a)无外场时锗烯的电子能带结构; (b)交换场强度为
$M=0.09t$ 时的电子能带结构; 其中实心(空心)三角表示上(下)边缘态, 圆点表示体能带, 红色(蓝色)对应自旋向上(向下)的电子; (c)交换场强度为$M=0.09t$ 时自旋相关电导随着电子能量的变化Fig. 3. (a) Energy-band diagram of germanene without external field; (b) energy-band diagram of germanene with local exchange field
$M=0.09t$ ; the solid (hollow) triangle represents the upper (lower) edge state, the dot represents the energy band, the red (blue) colour corresponds to the spin-up (spin-down) electron; (c) the spin-dependent conductance as a function of electronic energy when$M=0.09t$ .图 4 (a)局域交换场和电场强度为
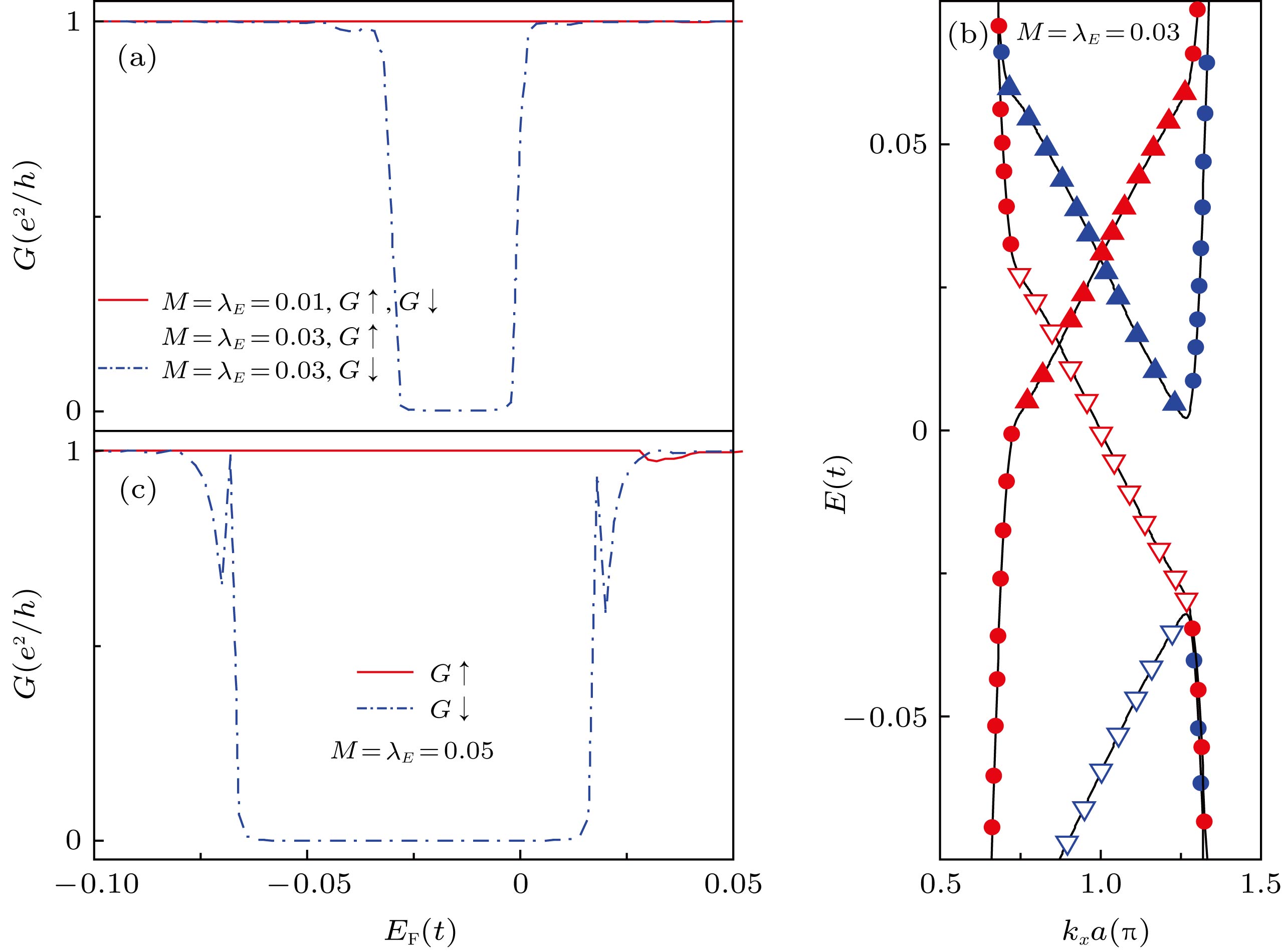
$M=\lambda_E=0.01t$ 和$M=\lambda_E=0.03t$ 时自旋相关电导随着电子费米能量$E_{\rm F}$ 的变化; (b)交换场和电场强度为$M=\lambda_E=0.05t$ 时自旋相关电导随着电子费米能量$E_{\rm F}$ 的变化; (c)交换场和电场强度为$M=\lambda_E=0.03t$ 时的电子能带结构; 其中实心(空心)三角表示上(下)边缘态, 圆点表示体能带, 红色(蓝色)对应自旋向上(向下)的电子Fig. 4. (a) The spin-dependent conductance as a function of electron Fermi energy
$E_{\rm F}$ when$M=\lambda_E=0.01t$ and$M=\lambda_E=0.03t$ ; (b) the spin-dependent conductance vs electron Fermi energy$E_{\rm F}$ when$M=\lambda_E=0.05t$ ; (c) energy-band diagram of germanene with local exchange field and electric field$M=\lambda_E=0.03t$ . The solid (hollow) triangle represents the upper (lower) edge state, the dot represents the energy band, the red (blue) colour corresponds to the spin-up (spin-down) electron. -
[1] Geim A K, Novoselov K S 2006 Nat. Mater. 6 183
[2] Neto A H C, Guinea F, Peres N M R, Novoselov K S, Geim A K 2009 Rev. Mod. Phys. 81 109
 Google Scholar
Google Scholar
[3] Takeda K, Shiraishi K 1994 Phys. Rev. B 50 14916
 Google Scholar
Google Scholar
[4] Cahangirov S, Topsakal M, Akturk E, Sahin H, Ciraci S 2009 Phys. Rev. Lett. 102 236804
 Google Scholar
Google Scholar
[5] Liu C C, W X Feng W X, Yao Y G 2011 Phys. Rev. Lett. 107 076802
 Google Scholar
Google Scholar
[6] Seixas L, Padilha J E, Fazzio A 2014 Phys. Rev. B 89 195403
 Google Scholar
Google Scholar
[7] 秦志辉 2017 66 216802
 Google Scholar
Google Scholar
Qin Z H 2017 Acta Phys. Sin. 66 216802
 Google Scholar
Google Scholar
[8] Vogt P, Padova P D, Quaresima C, Avila J, Frantzeskakis E, Asensio M C, Resta A, Ealet A, Lay G L 2012 Phys. Rev. Lett. 108 155501
 Google Scholar
Google Scholar
[9] Fleurence A, Friedlein R, Ozaki T, Kawai H, Wang Y, Takamura Y Y 2012 Phys. Rev. Lett. 108 245501
 Google Scholar
Google Scholar
[10] Meng L, Wang Y L, Zhang L Z, Du S X, Wu R T, Li L F, Zhang Y, Li G, Zhou H T, Hofer W A, Gao H J 2013 Nano Lett. 13 685
 Google Scholar
Google Scholar
[11] Chiappe D, Scalise E, Cinquanta E, Grazianetti C, van den Broek B, Fanciulli M, Houssa M, Molle A 2014 Adv. Mater. 26 2096
 Google Scholar
Google Scholar
[12] Li L F, Lu S Z, Pan J B, Qin Z H, Wang Y Q, Wang Y L, Cao G Y, Du S X, Gao H 2014 J. Adv. Mater. 26 4820
 Google Scholar
Google Scholar
[13] Davila M E, Xian L, Cahangirov S, Rubio A, Le Lay G 2014 New J. Phys. 16 095002
 Google Scholar
Google Scholar
[14] Derivaz M, Dentel D, Stephan R, Hanf M C, Mehdaoui A, Sonnet P, Pirri C 2015 Nano Lett. 15 2510
 Google Scholar
Google Scholar
[15] Zhu F F, Chen W J, Xu Y, Gao C L, Guan D D, Liu C H, Qian D, Zhang S C, Jia J 2015 Nat. Mater. 14 1020
 Google Scholar
Google Scholar
[16] Zhang L, Bampoulis P, Rudenko A N, Yao Q, Houselt A V, Poelsema B, Katsnelson M I, Zandvliet H J W 2016 Phys. Rev. Lett. 116 256804
 Google Scholar
Google Scholar
[17] Tabert C J, Nicol E J 2013 Phys. Rev. B 87 235426
 Google Scholar
Google Scholar
[18] Rachel S, Ezawa M 2014 Phys. Rev. B 89 195303
 Google Scholar
Google Scholar
[19] Saxena R, Saha A, Rao S 2015 Phys. Rev. B 92 245412
 Google Scholar
Google Scholar
[20] Liu D P, Yu Z M, Liu Y L 2016 Phys. Rev. B 94 155112
 Google Scholar
Google Scholar
[21] Tao L L, Cheung K T, Zhang L, Wang J 2017 Phys. Rev. B 95 121407
 Google Scholar
Google Scholar
[22] Tian H Y, Wang S K, Hu J G, Wang J 2015 J. Phys.: Condens. Matter 27 125005
 Google Scholar
Google Scholar
[23] Ren C, Zhou B, Sun M, Wang S, Li Y 2018 Appl. Phys. Express 11 063006
 Google Scholar
Google Scholar
[24] Szafran B, Mreńca-Kolasińska A, Rzeszotarski B 2018 Phys. Rev. B 97 165303
 Google Scholar
Google Scholar
[25] Zheng J, Chi F, Guo Y 2018 Phys. Rev. Appl. 9 024012
 Google Scholar
Google Scholar
[26] Zheng J, Chi F, Guo Y 2018 Appl. Phys. Lett. 113 112404
 Google Scholar
Google Scholar
[27] Luo M 2019 Phys. Rev. B 99 165407
 Google Scholar
Google Scholar
[28] Verma S, Kundu A 2019 Phys. Rev. B 99 121409
 Google Scholar
Google Scholar
[29] Ziese M, Thornton M J 2001 Spin Electronics (New York: Springer-Verlag) pp396−415
[30] Fert A 2008 Rev. Mod. Phys. 80 1517
 Google Scholar
Google Scholar
[31] 郭永, 顾秉林, 川添良幸 2000 49 1814
 Google Scholar
Google Scholar
Guo Y, Gu B L, Yoshiyuki K 2000 Acta Phys. Sin. 49 1814
 Google Scholar
Google Scholar
[32] Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 146802
 Google Scholar
Google Scholar
[33] Ezawa M 2012 Phys. Rev. Lett. 109 055502
 Google Scholar
Google Scholar
[34] Meir Y, Wingreen N S 1992 Phys. Rev. Lett. 68 2512
 Google Scholar
Google Scholar
[35] Lee D H, Joannopoulos J D 1981 Phys. Rev. B 23 4988
 Google Scholar
Google Scholar
[36] Lee D H, Joannopoulos J D 1981 Phys. Rev. B 23 4997
 Google Scholar
Google Scholar
计量
- 文章访问数: 13110
- PDF下载量: 104
- 被引次数: 0













 下载:
下载: