-
缝洞型介质通常具有非均质性强、结构多尺度的特征. 传统数值方法在解决此类多尺度流动问题时, 难以兼顾计算精度与计算效率, 无法实际应用. 对此, 本文提出了多孔介质流体流动的多尺度分解法, 并应用于缝洞介质流动模拟, 能够大幅减小计算的复杂度, 同时可以通过控制均化程度控制计算精度. 该方法将求解空间分为若干个子空间的正交直和, 从而获得一个近线性的计算复杂度; 以分层计算的方式实现了快速计算, 另外这种方法是一种无网格方法, 具有较好的地层适应性. 同时, 采用离散缝洞模型简化缝洞结构, 进一步提高了计算效率. 详细阐述了基于多尺度分解法的多孔介质流体流动数值计算格式的建立, 重点介绍了如何在不同的层次上计算基函数. 数值结果表明, 本文提出的计算方法不仅能够准确捕捉多孔介质中的精细流动特征, 而且具有很高的计算效率, 是一种有效的流动模拟方法.Numerical simulation of a fractured-vuggy porous medium is a challenging problem. One reason is the coexistence of matrix, fractures and vugs on multiple scales that need to be coupled, and the other reason is that the high-resolution fractured-vuggy model may contain up to several millions of gridcells in applications, which brings severe computational challenges into the numerical methods. Therefore, the requirement for accurate and efficient technique is widely increasing. Fractured-vuggy porous medium is generally represented by triple-continuum model in which the matrix system, fracture system and vug system each are treated as a parallel continuous system. Although triple-continuum model is widely used because of its easy-implementation and high efficiency, it fails to capture the detailed flow patterns of reservoir with disconnected long fractures. Discrete fracture-vug network (DFVN) model can precisely model the fluid flow in fractures and vugs. However, the simulation of this model is deemed intractable even with the advent of supercomputers because of the large amount of calculation. In view of the fact that the multigrid method is now well known as one of the fastest method of solving elliptic problems, in this paper we introduce a nearly linear complexity multiresolution decomposition method for fluid flow in a fractured-vuggy reservoir. The detailed flow patterns are described by combing the advantages of continuum model and discrete model. That is, the homogenization theory is used to construct an equivalent permeability in each coarse grid block in which the vugs and small-scale fractures are represented by discrete fracture-vug network model. We decompose the solution space into several subspaces and then we compute the corresponding solutions of heterogeneous discrete fracture network model in each subspace. Gamblets are constructed and they are elementary solutions of hierarchical information games associated with the process of computing with partial information and limited resources. These gamblets have a natural Bayesian interpretation under the mixed strategy emerging from the game theoretic formulation. This method could realize its fast simulation by decomposing the solution space into a direct sum of linear subspaces that are orthogonal to each other. Finally, the pressure difference distribution of fractured-vuggy porous medium is obtained by combing the DFVN solutions of all subspaces. Numerical results are presented to demonstrate the accuracy and efficiency of the proposed multiresolution decomposition method. The results show that this method is a promising method of numerically simulating the fractured-vuggy porous medium.
-
Keywords:
- fractured-vuggy porous media /
- multiresolution decomposition /
- discrete fracture-vug network model /
- numerical simulation
[1] Christie M A 1996 J. Pet. Sci. Technol. 48 1004
Google Scholar
[2] Durlofsky L J 1991 Water Resour. Res. 27 699
Google Scholar
[3] 张庆福, 黄朝琴, 姚军, 王月英 李阳 2017 科学通报 13 85
Zhang Q F, Huang Z Q, Yao J, Wang Y Y, Li Y 2017 Chin. Sci. Bull. 13 85
[4] Efendiev Y, Galvis J, Hou T Y 2013 J. Comput. Phys. 251 116
Google Scholar
[5] Zhang Q, Owhadi H, Yao J, Schäfer F, Huang Z, Li Y 2019 J. Comput. Phys. DOI: 10.1016/j.jcp.2018.12.032Google Scholar
[6] Juanes R 2005 Finite Elem. Anal. Des. 41 763
Google Scholar
[7] Zhang N, Wang Y, Sun Q, Wang Y 2018 Int. J. Heat. Mass. Tran. 116 484
Google Scholar
[8] Brandt A 1977 Math. Comput. 31 333
Google Scholar
[9] Hackbusch W 1989 Numer. Math. 56 229
Google Scholar
[10] Fedorenko R P 1961 Zh. Vychisl. Mat. Mat. Fiz. 1 922
Google Scholar
[11] Yavneh I 2006 Comput. Sci. Eng. 8 12
Google Scholar
[12] Engquist B, Luo E 1997 SIAM J. Numer. Anal. 34 2254
Google Scholar
[13] Wan W L, Chan T F, Smith B 1999 SIAM J. Sci. Comput. 21 1632
Google Scholar
[14] Brezina M, Cleary A J, Falgout R D, Henson V E, Jones J E, Manteuffel T A, Ruge J W 2001 SIAM J. Sci. Comput. 22 1570
Google Scholar
[15] Yserentant H 1986 Numer. Math. 49 379
Google Scholar
[16] Bank R E, Dupont T F, Yserentant H 1988 Numer. Math. 52 427
Google Scholar
[17] Axclsson O, Vassilevski P S 1989 Numer. Math. 56 157
Google Scholar
[18] Branets L V, Ghai S S, Lyons S L, Wu X H 2009 Commun. Comput. Phys. 6 1
Google Scholar
[19] Huang Z Q, Yao J, Li Y, Wang C, Lü X 2010 Sci. China: Technol. Sc. 53 839
Google Scholar
[20] 吴玉树, 葛家理 1983 力学学报 19 81
Wu Y S, Ge J L 1983 Chin. J. Theor. Appl. Mech. 19 81
[21] 姚军, 黄朝琴, 王子胜, 李亚军 2010 石油学报 31 815
Google Scholar
Yao J, Huang Z Q, Wang Z S, Li Y J 2010 Acta Petrolei Sinica 31 815
Google Scholar
[22] Huang Z Q, Yao J, Li Y, Wang C, Lv X 2011 Commun. Comput. Phys. 9 180
Google Scholar
[23] Owhadi H 2017 SIAM Rev. 59 99
Google Scholar
[24] Owhadi H, Zhang L 2017 J. Comput. Phys. 347 99
Google Scholar
[25] Chen Y, Durlofsky L J 2006 Transp. Porous Media 62 157
Google Scholar
[26] Yan X, Huang Z Q, Yao J, Li Y, Fan D 2016 15th European Conference on the Mathematics of Oil Recovery Amsterdam, the Netherlands, August 29, 2016 DOI: 10.3997/2214-4609.201601839
[27] Von Neumann J, Morgenstern O 1944 Theory of Games and Economic Behavior (Princeton: Princeton University Press) pp102−110
[28] Nash J 1951 Ann. Math. 54 286
Google Scholar
[29] Cao Z W, Liu Z F, Wang Y Z, Wang X H, Noetinger B 2018 Commun. Nonlinear Sci. 62 264
Google Scholar
[30] Liu Z F, Wang X H 2014 J. Comput. Phys. 278 169
Google Scholar
-
图 4 基函数
$\chi _i^{\left( k \right)}$ 示意图Fig. 4. Illustration of basis functions
$\chi _i^{\left( k \right)}$ .
图 6 (a)小尺度缝洞型油藏几何模型; (b)等效渗透率场图; (c) 多层网格系统
Fig. 6. (a) Geometrical model of a small-scale-fractured vuggy porous oil reservoir; (b) equivalent permeability of fractured-vuggy medium; (c) nested grid system.
图 7 对于小尺度缝洞模型, 参考解和多重网格解对比 (a) 参考解; (b) k = 3时的多重网格解
Fig. 7. Comparison of reference solution and gamblets solution for a small-scale-fractured vuggy porous medium: (a) Reference solution; (b) gamblets solution with k = 3.
图 8 长裂缝介质模型
Fig. 8. Geometrical model of a fractured-vuggy porous medium with a long fracture.
图 9 对于长裂缝模型, 参考解和多重网格解对比 (a)参考解; (b) k = 3时的多重网络解; (c) k = 2时的多重网格解
Fig. 9. Comparison of reference solution and gamblets solution for a fractured-vuggy porous medium with a long fracture: (a) Reference solution; (b) gamblets solution with k = 3; (c) gamblets solution with k = 2.
图 10 大尺度缝洞介质几何模型
Fig. 10. Geometrical model of a large-scale-fractured vuggy porous medium.
图 11 大尺度缝洞介质模型在各层上的解
Fig. 11. Solutions in different levels for a large-scale-fractured vuggy porous medium.
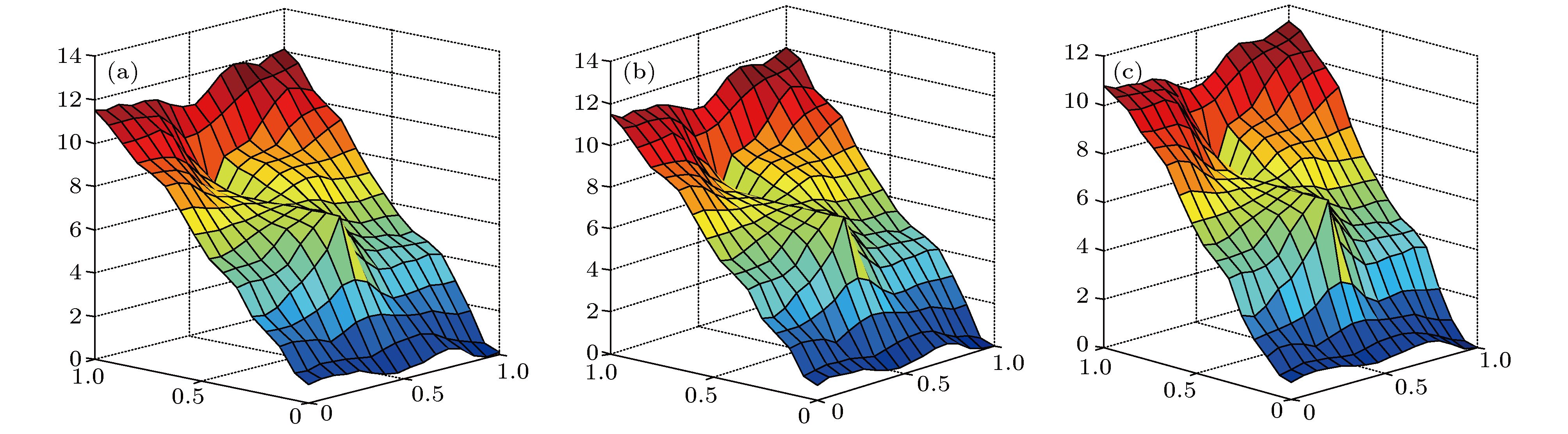
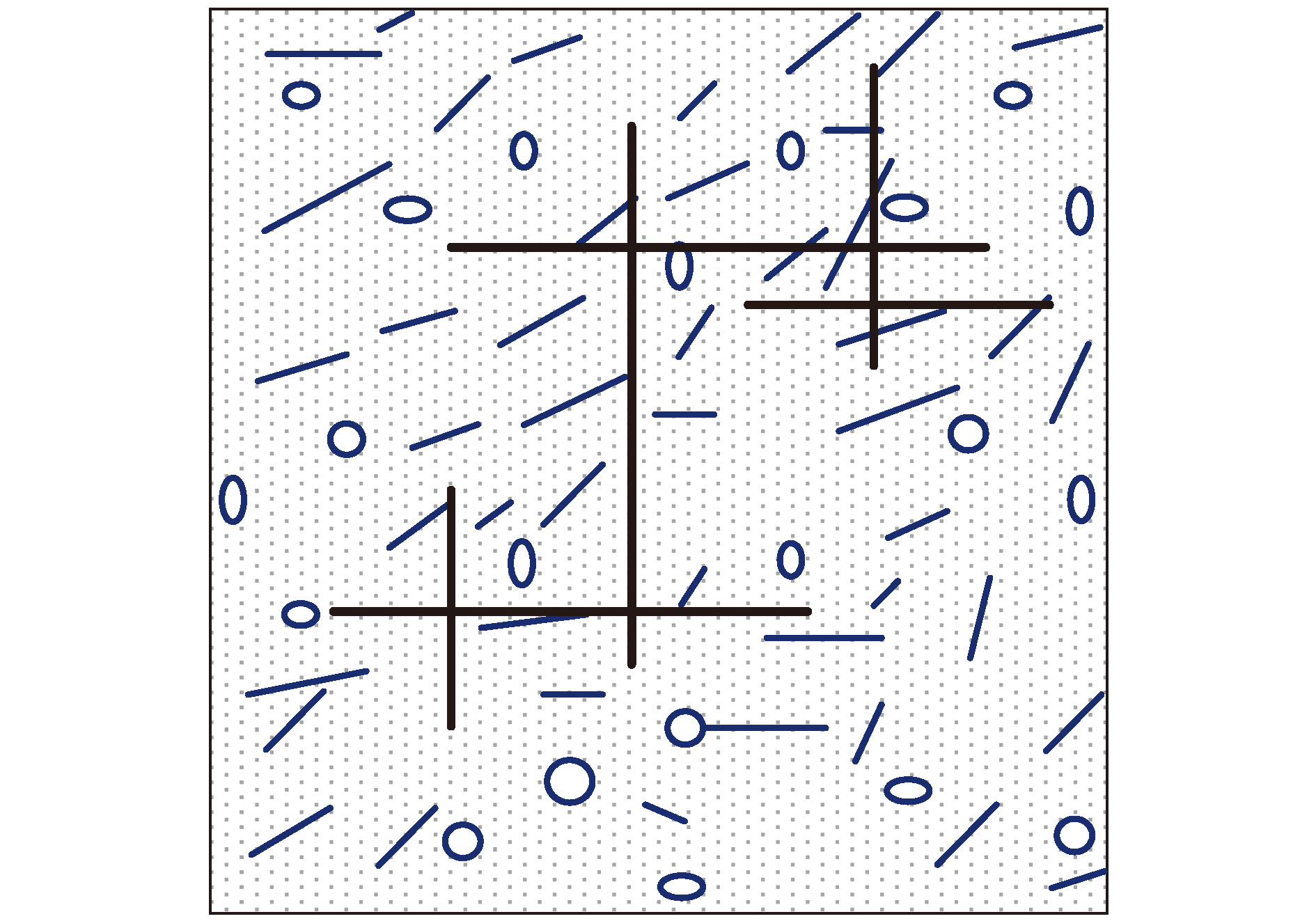
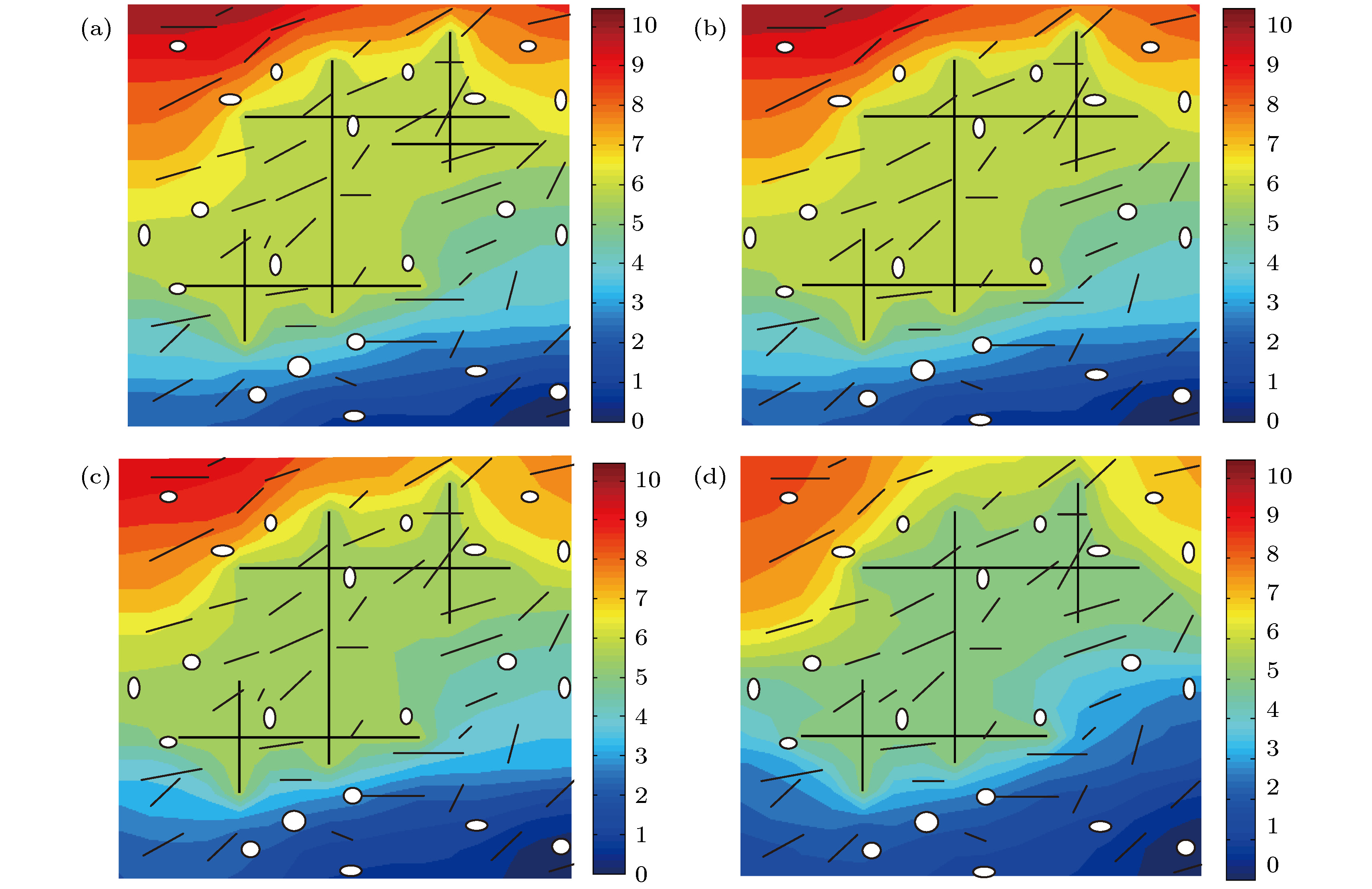
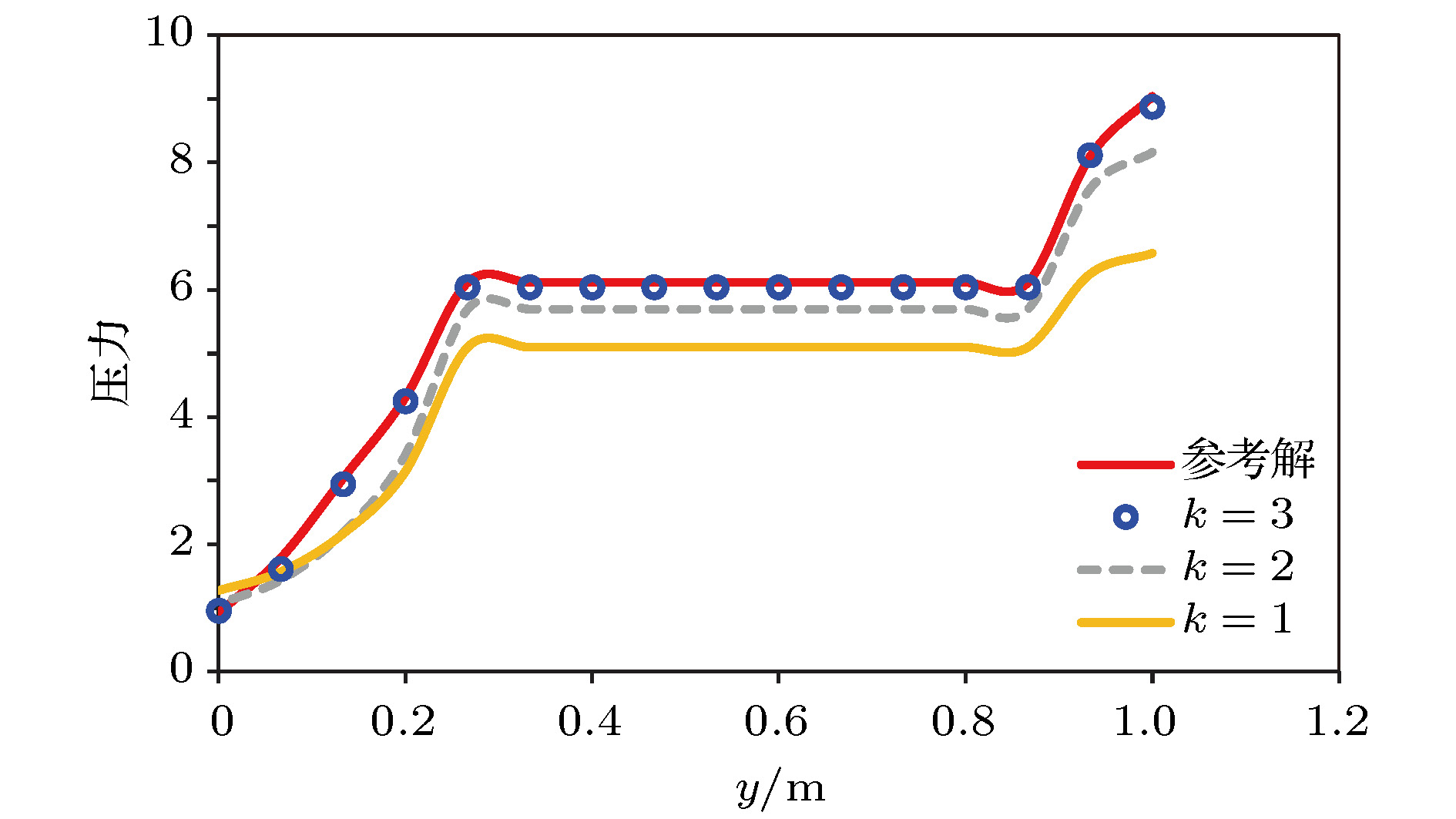
图 12 对于大尺度缝洞介质模型, 参考解和多重网格解对比 (a) 参考解; (b) k = 3时的多重网格解; (c) k = 2时的多重网格解; (d) k = 1时的多重网格解
Fig. 12. Comparison of reference solution and gamblets solution for a large-scale-fractured vuggy porous medium: (a) Reference solution; (b) gamblets solution with k = 3; (c) gamblets solution with k = 2; (d) gamblets solution with k = 1.
图 13 沿x = 5 m的参考解和不同均化程度下多重网格解对比曲线图
Fig. 13. Comparison of reference solution and gamblets solution with different k when x = 5 m.
表 1 裂缝性介质模型基本参数
Table 1. Parameters of fractured porous medium.
参数名称 参数值 裂缝渗透率/${\text{μ}}{\rm m}^2$ 1 × 104 裂缝开度/m 1 × 10–3 流体黏度/mPa·s 1 基岩渗透率/${\text{μ}}{\rm m}^2$ 0.001 
下载: 导出CSV
表 2 对于小尺度缝洞模型, 不同k时的计算误差
Table 2. Relative error in different k for a small-scale-fractured vuggy porous medium.
k 2 3 4 计算误差 0.0823 0.0132 3.2549 × 10–15
下载: 导出CSV
表 3 对于大尺度缝洞介质模型, 不同k时的计算误差
Table 3. Relative error with different k for a large-scale-fractured vuggy porous medium.
k 1 2 3 计算误差 0.1925 0.0831 0.0141
下载: 导出CSV
-
[1] Christie M A 1996 J. Pet. Sci. Technol. 48 1004
Google Scholar
[2] Durlofsky L J 1991 Water Resour. Res. 27 699
Google Scholar
[3] 张庆福, 黄朝琴, 姚军, 王月英 李阳 2017 科学通报 13 85
Zhang Q F, Huang Z Q, Yao J, Wang Y Y, Li Y 2017 Chin. Sci. Bull. 13 85
[4] Efendiev Y, Galvis J, Hou T Y 2013 J. Comput. Phys. 251 116
Google Scholar
[5] Zhang Q, Owhadi H, Yao J, Schäfer F, Huang Z, Li Y 2019 J. Comput. Phys. DOI: 10.1016/j.jcp.2018.12.032Google Scholar
[6] Juanes R 2005 Finite Elem. Anal. Des. 41 763
Google Scholar
[7] Zhang N, Wang Y, Sun Q, Wang Y 2018 Int. J. Heat. Mass. Tran. 116 484
Google Scholar
[8] Brandt A 1977 Math. Comput. 31 333
Google Scholar
[9] Hackbusch W 1989 Numer. Math. 56 229
Google Scholar
[10] Fedorenko R P 1961 Zh. Vychisl. Mat. Mat. Fiz. 1 922
Google Scholar
[11] Yavneh I 2006 Comput. Sci. Eng. 8 12
Google Scholar
[12] Engquist B, Luo E 1997 SIAM J. Numer. Anal. 34 2254
Google Scholar
[13] Wan W L, Chan T F, Smith B 1999 SIAM J. Sci. Comput. 21 1632
Google Scholar
[14] Brezina M, Cleary A J, Falgout R D, Henson V E, Jones J E, Manteuffel T A, Ruge J W 2001 SIAM J. Sci. Comput. 22 1570
Google Scholar
[15] Yserentant H 1986 Numer. Math. 49 379
Google Scholar
[16] Bank R E, Dupont T F, Yserentant H 1988 Numer. Math. 52 427
Google Scholar
[17] Axclsson O, Vassilevski P S 1989 Numer. Math. 56 157
Google Scholar
[18] Branets L V, Ghai S S, Lyons S L, Wu X H 2009 Commun. Comput. Phys. 6 1
Google Scholar
[19] Huang Z Q, Yao J, Li Y, Wang C, Lü X 2010 Sci. China: Technol. Sc. 53 839
Google Scholar
[20] 吴玉树, 葛家理 1983 力学学报 19 81
Wu Y S, Ge J L 1983 Chin. J. Theor. Appl. Mech. 19 81
[21] 姚军, 黄朝琴, 王子胜, 李亚军 2010 石油学报 31 815
Google Scholar
Yao J, Huang Z Q, Wang Z S, Li Y J 2010 Acta Petrolei Sinica 31 815
Google Scholar
[22] Huang Z Q, Yao J, Li Y, Wang C, Lv X 2011 Commun. Comput. Phys. 9 180
Google Scholar
[23] Owhadi H 2017 SIAM Rev. 59 99
Google Scholar
[24] Owhadi H, Zhang L 2017 J. Comput. Phys. 347 99
Google Scholar
[25] Chen Y, Durlofsky L J 2006 Transp. Porous Media 62 157
Google Scholar
[26] Yan X, Huang Z Q, Yao J, Li Y, Fan D 2016 15th European Conference on the Mathematics of Oil Recovery Amsterdam, the Netherlands, August 29, 2016 DOI: 10.3997/2214-4609.201601839
[27] Von Neumann J, Morgenstern O 1944 Theory of Games and Economic Behavior (Princeton: Princeton University Press) pp102−110
[28] Nash J 1951 Ann. Math. 54 286
Google Scholar
[29] Cao Z W, Liu Z F, Wang Y Z, Wang X H, Noetinger B 2018 Commun. Nonlinear Sci. 62 264
Google Scholar
[30] Liu Z F, Wang X H 2014 J. Comput. Phys. 278 169
Google Scholar
下载:
计量
- 文章访问数: 7198
- PDF下载量: 76
- 被引次数: 0
