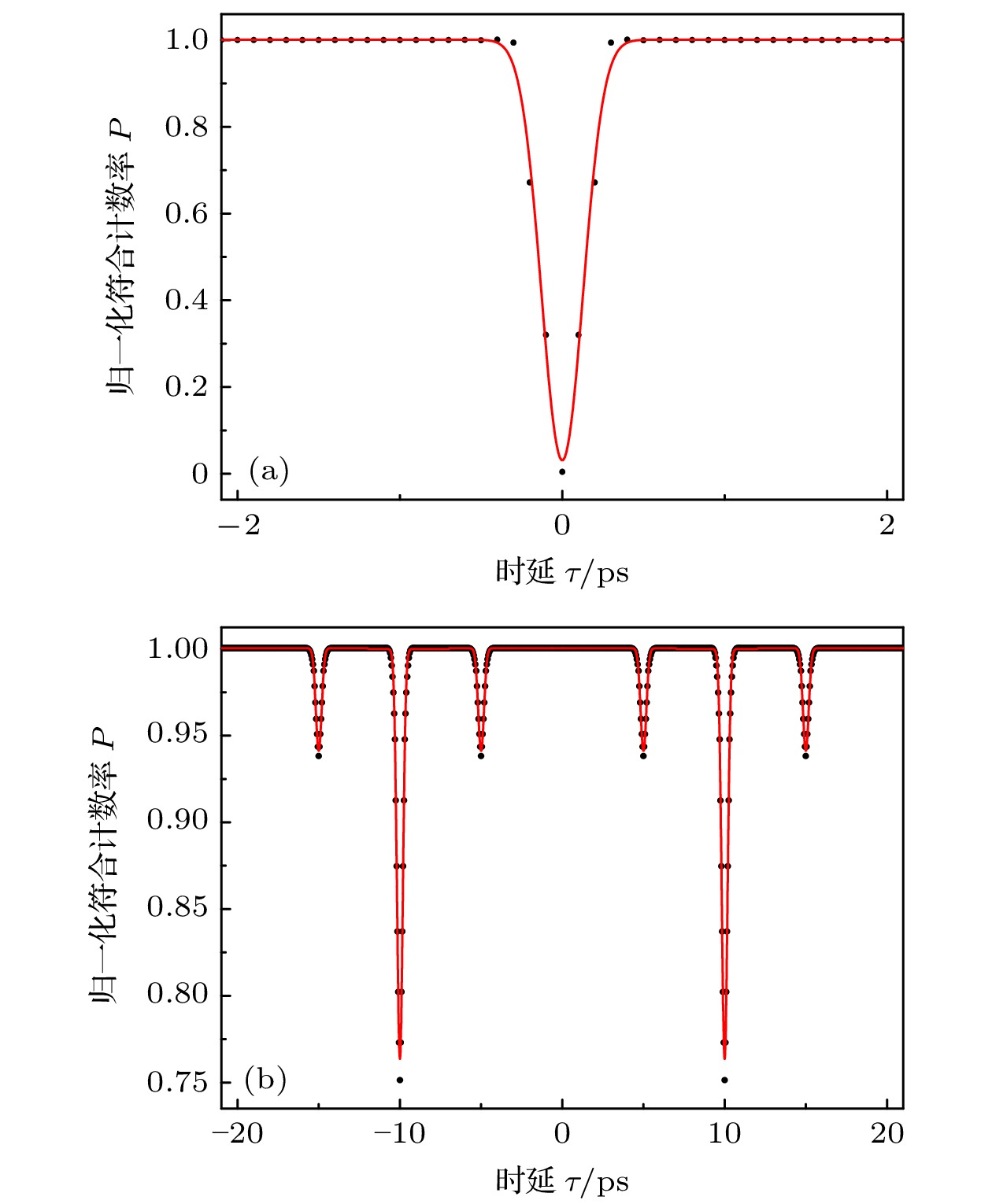
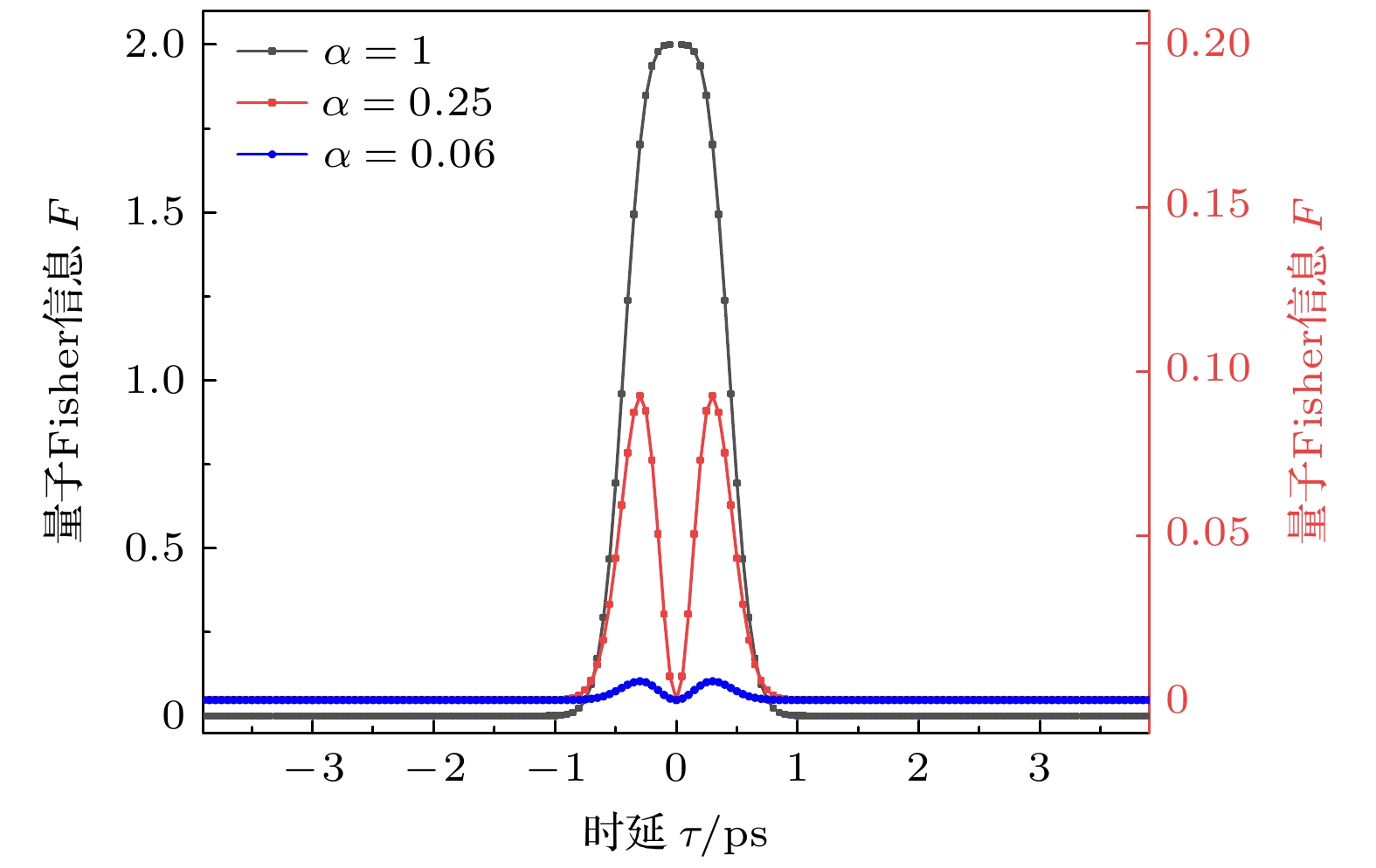
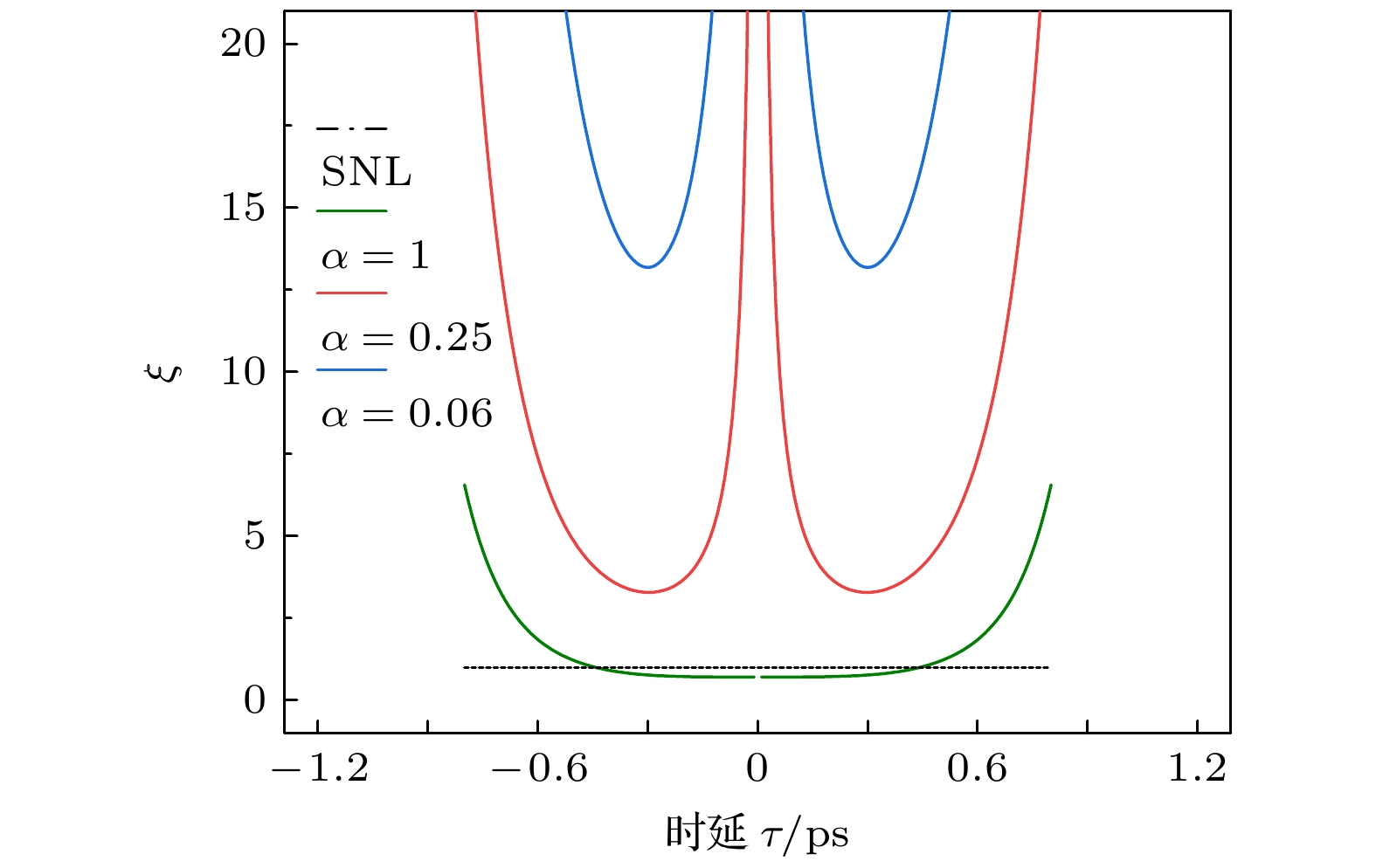
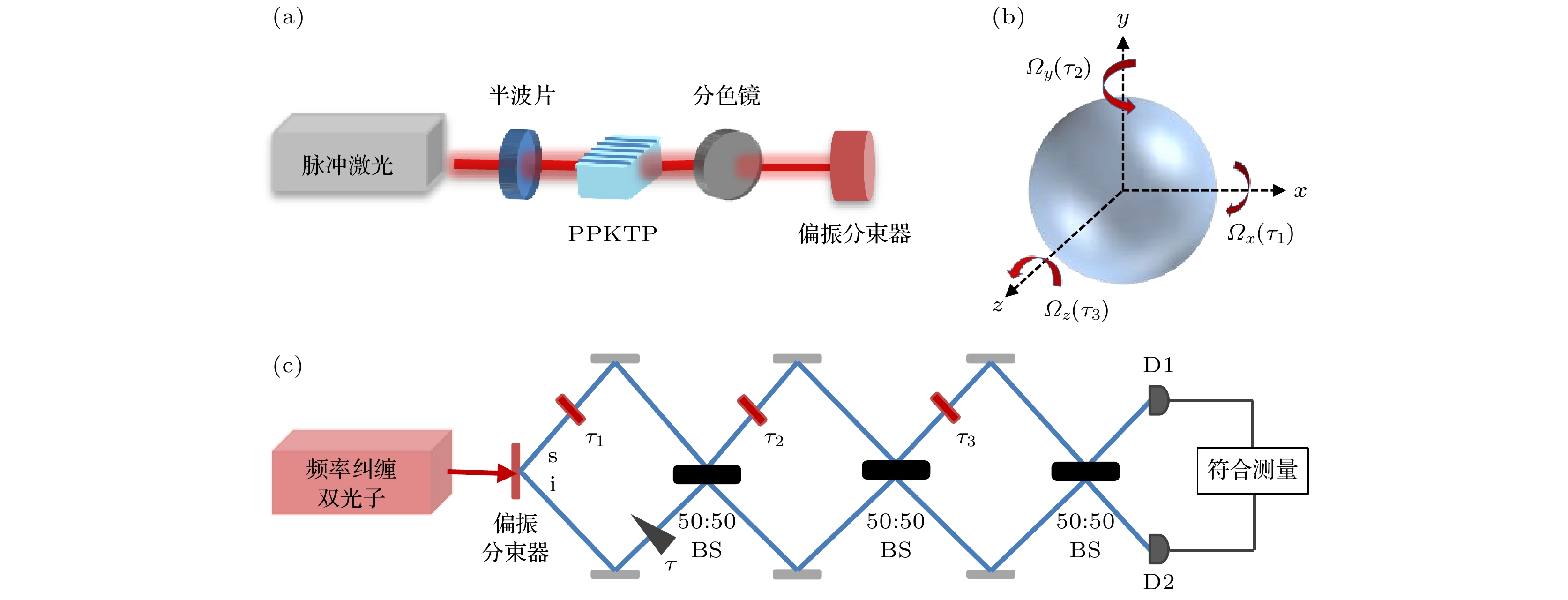
-
高时延分辨率的Hong-Ou-Mandel(HOM)干涉仪一直是量子精密测量领域的研究热点, 将其应用到量子陀螺仪中可以实现突破经典理论极限的角速度测量. 本文提出了基于频率纠缠双光子和级联HOM干涉仪的量子陀螺仪方案. 利用信号光和闲置光之间由于旋转存在的Sagnac效应, 将三轴角速度分别引入到级联HOM干涉仪中的对应测量臂, 利用级联HOM干涉图谱中凹陷位置与多个独立时延差之间的对应关系, 结合干涉可见度与量子Fisher信息理论, 得到3个独立时延差($ {\tau }_{1} $, $ {\tau }_{2} $, $ {\tau }_{3} $)的最大量子Fisher信息分别为(2, 0.1, 0.006). 通过引入测量不确定度, 得出时延值测量精度可以突破散粒噪声极限, 并结合时延差与旋转角速度的关系, 可实现三轴角速度的测量, 且测量精度可以超越经典光学陀螺仪, 方案可为后续量子陀螺仪在全球导航传感领域的进一步应用提供理论支持.
-
关键词:
- 级联Hong-Ou-Mandel干涉 /
- 频率纠缠双光子 /
- 量子陀螺仪
The optical gyroscope for measuring the attitude information of spatial carriers, has emerged as a research hotspot in inertial navigation system. Real-time measurement of rotation angular velocity is crucial for obtaining accurate attitude information. However, the measurement accuracy of traditional optical gyroscope is limited by the short noise limit (SNL), which restricts its further applications. Existing research indicates that the quantum technology is needed to address the measurement limitations of traditional optical gyroscopes. A triaxial rotation angular velocity measurement scheme based on frequency entangled biphoton and cascaded Hong-Ou-Mandel (HOM) interference is proposed in this study. By using the Sagnac effect induced by the rotation between signal and idler photons, the triaxial angular velocity is introduced into the corresponding measurement arm of a cascaded HOM interferometer. The cascaded HOM interferogram is obtained using a coincidence measurement device, and the relationship between the symmetric dip position and the three independent time delay difference is analyzed. The characteristic parameters of HOM interferogram, including a half-height full width (FWHM) of 0.3 ps and visibilities of 1, 0.25 and 0.06, respectively, are obtained. According to quantum Fisher information theory, the maximum quantum Fisher information values of the three independent time delay differences ($ {\tau }_{1} $, $ {\tau }_{2} $, $ {\tau }_{3} $) are calculated to be 1, 0.1, and 0.006, respectively. Furthermore, by incorporating measurement uncertainty, it is demonstrated that the accuracy of the time delay measurement can exceed the SNL. Combined with the relationship between time delay and angular velocity, the results show that the angular velocity measurement accuracy exceeds that of classical optical gyroscopes. Therefore, this scheme provides a theoretical foundation for further applying quantum gyroscopes to global navigation sensing and precision measurement systems.[1] Toland J R E, Search C P 2013 Appl. Phys. B 114 333
Google Scholar
[2] Aghaie K Z, Digonnet M J F 2015 J. Opt. Soc. Am. B 32 339
Google Scholar
[3] 陈坤, 陈树新, 吴德伟, 杨春燕, 吴昊 2016 65 054203
Google Scholar
Chen K, Chen S X, Wu D W, Yang C Y, Wu H 2016 Acta Phys. Sin. 65 054203
Google Scholar
[4] Lefèvre H C 2014 C. R. Physique 15 851
Google Scholar
[5] Sultana J 2014 Gen. Relat. Gravti. 46 1710
Google Scholar
[6] Courtney T L, Park S D, Hill R J, Cho B, Jonas D M 2014 Opt. Lett. 39 513
Google Scholar
[7] Giovannetti V, Lloyd S, Maccone L 2001 Nature 412 417
Google Scholar
[8] Dowling J P 2008 Contemp. Phys. 49 125
Google Scholar
[9] Kura N, Ueda M 2020 Phys. Rev. Lett. 124 010507
Google Scholar
[10] Fink M, Rodriguez-Aramendia A, Handsteiner J, Ziarkash A, Steinlechner F, Scheidl T, Fuentes I, Pienaar J, Ralph T C, Ursin R 2016 Nat. Commun. 8 15304
Google Scholar
[11] O'Donnell K A 2011 Phys. Rev. Lett. 106 063601
Google Scholar
[12] Baek S Y, Cho Y W, Kim Y H 2009 Opt. Express 17 19241
Google Scholar
[13] Kolkiran A, Agarwal G S 2007 Opt. Express 15 6798
Google Scholar
[14] Fink M, Steinlechner F, Handsteiner J, Dowling J P, Scheidl T, Ursin R 2019 New J. Phys. 21 053010
Google Scholar
[15] Silvestri R, Yu H C, Stromeberg T, Hilweg C, Peterson R W, Walther P 2024 Sci. Adv. 10 0215
Google Scholar
[16] Scully M O, Zubairy M S 1997 Quantum Optics (Cambridge University Press) pp271–290
[17] Lyons A, Knee G C, Bolduc E, Thomas R, Leach J, Gauger E M, Faccio D 2018 Sci. Adv. 4 9416
Google Scholar
[18] Chen Y Y, Fink M, Steinlechner F, Torres J P, Ursin R 2019 npj Quantum Inform. 5 43
Google Scholar
[19] Valencia A, Scarcelli G, Shih Y H 2004 Appl. Phys. Lett. 85 2655
Google Scholar
[20] 徐耀坤, 孙仕海, 曾瑶源, 杨俊刚, 盛卫东, 刘伟涛 2023 72 214207
Google Scholar
Xu Y K, Sun S H, Zeng Y Y, Yang J G, Sheng W D, Liu W T 2023 Acta Phys. Sin. 72 214207
Google Scholar
[21] 罗一振, 马洛嘉, 孙铭烁, 吴思睿, 邱丽华, 王禾, 王琴 2024 73 240302
Google Scholar
Luo Y Z, Ma L J, Sun M S, Wu S R, Qiu L H, Wang H, Wang Q 2024 Acta Phys. Sin. 73 240302
Google Scholar
[22] Liu R, Kong L J, Wang Z X, Si Y, Qi W R, Huang S Y, Tu C H, Li Y N, Wang H T 2018 Chin. Phys. Lett. 35 090303
Google Scholar
[23] Ma L J, Sun M S, Zhang C H, Ding H J, Zhou X Y, Li J, Wang Q 2025 Chin. Phys. B 34 010301
Google Scholar
[24] Gao W L, Xu L P, Zhang H, Yan B, Li P X, Hu G T 2023 Chin. Phys. B 32 050304
Google Scholar
[25] Yang Y, Xu L P, Giovannetti V 2019 Phys. Rev. A 100 063810
Google Scholar
[26] Post E J 1967 Rev. Mod. Phys. 39 475
Google Scholar
[27] 翟艺伟, 董瑞芳, 权润爱, 项晓, 刘涛, 张首刚 2021 70 120302
Google Scholar
Zhai Y W, Dong R F, Quan R A, Xiang X, Liu T, Zhang S G 2021 Acta Phys. Sin. 70 120302
Google Scholar
[28] Braunstein S L, Caves C M 1994 Phys. Rev. Lett. 72 3439
Google Scholar
[29] 任志红, 李岩, 李艳娜, 李卫东 2019 68 040601
Google Scholar
Ren Z H, Li Y, Li Y N, Li W D 2019 Acta Phys. Sin. 68 040601
Google Scholar
[30] Zwierz M, Pérez-Delgado C A, Kok P 2010 Phys. Rev. Lett. 105 180402
Google Scholar
[31] Giovannetti V, Lloyd S, Maccone L 2006 Phys. Rev. Lett. 96 010401
Google Scholar
[32] Guo Y, Yang Z X, Zeng Z Q, Ding C L, Shimizu R, Jin R B 2023 Opt. Express 31 32849
Google Scholar
[33] Kok P, Dunningham J, Ralph J F 2017 Phys. Rev. A 95 012326
Google Scholar
-
图 1 (a) 频率纠缠双光子源; (b) 旋转空间目标; (c) 基于频率纠缠双光子的级联HOM干涉仪原理框图
Fig. 1. (a) Frequency entangled biphoton source; (b) rotation space target; (c) diagram of cascaded HOM interferometer based on frequency entangled biphoton.
图 2 (a) 频率纠缠双光子的标准HOM干涉图谱; (b) 级联HOM干涉图谱
Fig. 2. (a) Standard HOM interferogram of frequency entangled biphoton; (b) the cascaded HOM interferogram.
图 3 $ \sigma =0.3\;{\mathrm{p}}{\mathrm{s}} $时, 不同干涉可见度$ \alpha $值下$ F $随$ \tau $的变化
Fig. 3. Variation of quantum Fisher information $ F $ with time delay $ \tau $ in different interference visibility $ \alpha $ at $ \sigma =0.3\;{\mathrm{p}}{\mathrm{s}} $.
-
[1] Toland J R E, Search C P 2013 Appl. Phys. B 114 333
Google Scholar
[2] Aghaie K Z, Digonnet M J F 2015 J. Opt. Soc. Am. B 32 339
Google Scholar
[3] 陈坤, 陈树新, 吴德伟, 杨春燕, 吴昊 2016 65 054203
Google Scholar
Chen K, Chen S X, Wu D W, Yang C Y, Wu H 2016 Acta Phys. Sin. 65 054203
Google Scholar
[4] Lefèvre H C 2014 C. R. Physique 15 851
Google Scholar
[5] Sultana J 2014 Gen. Relat. Gravti. 46 1710
Google Scholar
[6] Courtney T L, Park S D, Hill R J, Cho B, Jonas D M 2014 Opt. Lett. 39 513
Google Scholar
[7] Giovannetti V, Lloyd S, Maccone L 2001 Nature 412 417
Google Scholar
[8] Dowling J P 2008 Contemp. Phys. 49 125
Google Scholar
[9] Kura N, Ueda M 2020 Phys. Rev. Lett. 124 010507
Google Scholar
[10] Fink M, Rodriguez-Aramendia A, Handsteiner J, Ziarkash A, Steinlechner F, Scheidl T, Fuentes I, Pienaar J, Ralph T C, Ursin R 2016 Nat. Commun. 8 15304
Google Scholar
[11] O'Donnell K A 2011 Phys. Rev. Lett. 106 063601
Google Scholar
[12] Baek S Y, Cho Y W, Kim Y H 2009 Opt. Express 17 19241
Google Scholar
[13] Kolkiran A, Agarwal G S 2007 Opt. Express 15 6798
Google Scholar
[14] Fink M, Steinlechner F, Handsteiner J, Dowling J P, Scheidl T, Ursin R 2019 New J. Phys. 21 053010
Google Scholar
[15] Silvestri R, Yu H C, Stromeberg T, Hilweg C, Peterson R W, Walther P 2024 Sci. Adv. 10 0215
Google Scholar
[16] Scully M O, Zubairy M S 1997 Quantum Optics (Cambridge University Press) pp271–290
[17] Lyons A, Knee G C, Bolduc E, Thomas R, Leach J, Gauger E M, Faccio D 2018 Sci. Adv. 4 9416
Google Scholar
[18] Chen Y Y, Fink M, Steinlechner F, Torres J P, Ursin R 2019 npj Quantum Inform. 5 43
Google Scholar
[19] Valencia A, Scarcelli G, Shih Y H 2004 Appl. Phys. Lett. 85 2655
Google Scholar
[20] 徐耀坤, 孙仕海, 曾瑶源, 杨俊刚, 盛卫东, 刘伟涛 2023 72 214207
Google Scholar
Xu Y K, Sun S H, Zeng Y Y, Yang J G, Sheng W D, Liu W T 2023 Acta Phys. Sin. 72 214207
Google Scholar
[21] 罗一振, 马洛嘉, 孙铭烁, 吴思睿, 邱丽华, 王禾, 王琴 2024 73 240302
Google Scholar
Luo Y Z, Ma L J, Sun M S, Wu S R, Qiu L H, Wang H, Wang Q 2024 Acta Phys. Sin. 73 240302
Google Scholar
[22] Liu R, Kong L J, Wang Z X, Si Y, Qi W R, Huang S Y, Tu C H, Li Y N, Wang H T 2018 Chin. Phys. Lett. 35 090303
Google Scholar
[23] Ma L J, Sun M S, Zhang C H, Ding H J, Zhou X Y, Li J, Wang Q 2025 Chin. Phys. B 34 010301
Google Scholar
[24] Gao W L, Xu L P, Zhang H, Yan B, Li P X, Hu G T 2023 Chin. Phys. B 32 050304
Google Scholar
[25] Yang Y, Xu L P, Giovannetti V 2019 Phys. Rev. A 100 063810
Google Scholar
[26] Post E J 1967 Rev. Mod. Phys. 39 475
Google Scholar
[27] 翟艺伟, 董瑞芳, 权润爱, 项晓, 刘涛, 张首刚 2021 70 120302
Google Scholar
Zhai Y W, Dong R F, Quan R A, Xiang X, Liu T, Zhang S G 2021 Acta Phys. Sin. 70 120302
Google Scholar
[28] Braunstein S L, Caves C M 1994 Phys. Rev. Lett. 72 3439
Google Scholar
[29] 任志红, 李岩, 李艳娜, 李卫东 2019 68 040601
Google Scholar
Ren Z H, Li Y, Li Y N, Li W D 2019 Acta Phys. Sin. 68 040601
Google Scholar
[30] Zwierz M, Pérez-Delgado C A, Kok P 2010 Phys. Rev. Lett. 105 180402
Google Scholar
[31] Giovannetti V, Lloyd S, Maccone L 2006 Phys. Rev. Lett. 96 010401
Google Scholar
[32] Guo Y, Yang Z X, Zeng Z Q, Ding C L, Shimizu R, Jin R B 2023 Opt. Express 31 32849
Google Scholar
[33] Kok P, Dunningham J, Ralph J F 2017 Phys. Rev. A 95 012326
Google Scholar
下载:
计量
- 文章访问数: 2744
- PDF下载量: 91
- 被引次数: 0
