一种新型复合指数型局部有源忆阻器耦合的Hopfield神经网络

王梦蛟; 杨琛; 贺少波; 李志军

doi:10.7498/aps.73.20231888

摘要

由忆阻耦合的神经网络模型, 因其能更真实地反映生物神经系统的复杂动力学特性而被广泛研究. 目前用于耦合神经网络的忆阻器数学模型主要集中在一次函数、绝对值函数、双曲正切函数等, 为进一步丰富忆阻耦合神经网络模型, 且考虑到一些掺杂半导体中粒子的运动规律, 设计了一种新的复合指数型局部有源忆阻器, 并将其作为耦合突触用于Hopfield神经网络, 利用基本的动力学分析方法, 研究了系统在不同参数下的动力学行为, 以及在不同初始值下多种分岔模式共存的现象. 实验结果表明, 忆阻突触内部参数对系统具有调控作用, 且该系统拥有丰富的动力学行为, 包括对称吸引子共存、非对称吸引子共存、大范围的混沌状态和簇发振荡等. 最后, 用STM32单片机对系统进行了硬件实现.

关键词:

Abstract

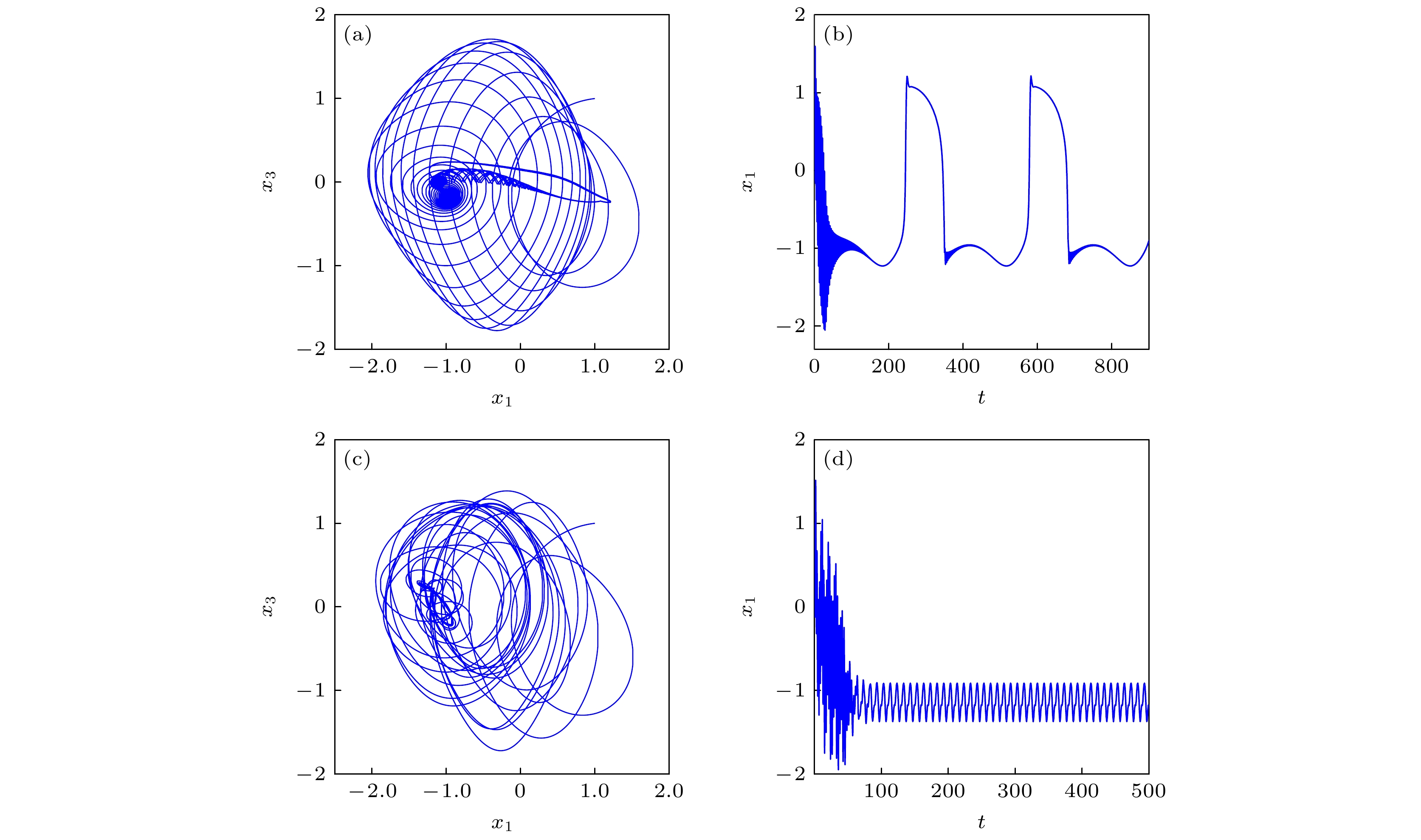
The neural network model coupled with memristors has been extensively studied due to its ability to more accurately represent the complex dynamic characteristics of the biological nervous system. Currently, the mathematical model of memristor used to couple neural networks mainly focuses on primary function, absolute value function, hyperbolic tangent function, etc. To further enrich the memristor-coupled neural network model and take into account the motion law of particles in some doped semiconductors, a new compound exponential local active memristor is proposed and used as a coupling synapse in the Hopfield neural network. Using the basic dynamic analysis method, the system’s dynamic behaviors are studied under different parameters and the coexistence of multiple bifurcation modes under different initial values. In addition, the influence of frequency change of external stimulation current on the system is also studied. The experimental results show that the internal parameters of memristor synapses regulate the system, and the system has a rich dynamic behavior, including symmetric attractor coexistence, asymmetric attractor coexistence, large-scale chaos as shown in attached figure, and bursting oscillation. Finally, the hardware of the system is realized by the STM32 microcontroller, and the experimental results verify the realization of the system.

Keywords:

作者及机构信息

1.
湘潭大学自动化与电子信息学院, 湘潭　411105

2.
湘潭大学物理与光电工程学院, 湘潭　411105

通信作者: 王梦蛟, wangmj@xtu.edu.cn

基金项目: 国家自然科学基金(批准号: 62071411)资助的课题.

Authors and contacts

1.
School of Automation and Electronic Information, Xiangtan University, Xiangtan 411105, China

2.
School of Physics and Optoelectronic Engineering, Xiangtan University, Xiangtan 411105, China

Corresponding author: Wang Meng-Jiao, wangmj@xtu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 62071411).

文章全文

参考文献

[1]	Chua L 1971 IEEE Trans. Circuits Syst. I Regul. Pap. 18 507 Google Scholar
[2]	Chua L 2014 Semicond. Sci. Technol. 29 104001 Google Scholar
[3]	Wang M J, Deng Y, Liao X H, Li Z J, Ma M L, Zeng Y C 2019 Int. J. Non. Linear. Mech. 111 149 Google Scholar
[4]	Peng Y X, Liu J, He S B, Sun K H 2023 Chaos, Solitons Fractals 171 113429 Google Scholar
[5]	Wang M J, An M Y, He S B, Zhang X N, Iu H H, Li Z J 2023 Chaos 33 073129 Google Scholar
[6]	Peng Y X, He S B, Sun K H 2022 Nonlinear Dyn. 107 1263 Google Scholar
[7]	He S B, Liu J, Wang H H, Sun K H 2023 Neurocomputing (Amst. ) 523 1 Google Scholar
[8]	古亚娜, 梁燕, 王光义, 夏晨阳 2022 71 110501 Google Scholar Gu Y N, Liang Y, Wang G Y, Xia C Y 2022 Acta Phys. Sin. 71 110501 Google Scholar
[9]	武长春, 周莆钧, 王俊杰, 李国, 胡绍刚, 于奇, 刘洋 2022 71 148401 Google Scholar Wu C C, Zhou P J, Wang J J, Li G, Hu S G, Yu Q, Liu Y 2022 Acta Phys. Sin. 71 148401 Google Scholar
[10]	Chua L 2013 Nanotechnology 24 383001 Google Scholar
[11]	Lu Y C, Li H M, Li C L 2023 Neurocomputing (Amst. ) 544 126246 Google Scholar
[12]	Li Z J, Chen K J 2023 Chaos, Solitons Fractals 175 114017 Google Scholar
[13]	Hopfield J J 1984 Proc. Natl. Acad. Sci. U. S. A. 81 3088 Google Scholar
[14]	Chen C J, Chen J Q, Bao H, Chen M, Bao B C 2019 Nonlinear Dyn. 95 3385 Google Scholar
[15]	Lin H R, Wang C H, Hong Q H, Sun Y C 2020 IEEE Tran. Circuits Syst. II Express Briefs 67 3472 Google Scholar
[16]	Chen C J, Min F H, Zhang Y Z, Bao B C 2021 Nonlinear Dyn. 106 2559 Google Scholar
[17]	Li C L, Yang Y Y, Yang X B, Zi X Y, Xiao F L 2022 Nonlinear Dyn. 108 1697 Google Scholar
[18]	Doubla I S, Ramakrishnan B, Njitacke Z T, Kengne J, Rajagopal K 2022 Int. J. Electron. Commun. 144 154059 Google Scholar
[19]	黄丽丽, 黄强, 黄振, 臧红岩, 雷腾飞 2023 电子元件与材料 42 10 Google Scholar Huang L L, Huang Q, Huang Z, Zang H Y, Lei T F 2023 Electron. Compon. Mater. 42 10 Google Scholar
[20]	Lin H R, Wang C H, Sun J R, Zhang X, Sun Y C, Iu H H C 2023 Chaos Solitons Fractals 166 112905 Google Scholar
[21]	Wan Q Z, Chen S M, Yang Q, Liu J, Sun K L 2023 Nonlinear Dyn. 111 18505 Google Scholar
[22]	Lin H R, Wang C H, Yu F, Sun J R, Du S C, Deng Z K, Deng Q L 2023 Mathematics (Basel) 11 1369 Google Scholar
[23]	Panahi S, Aram Z, Jafari S, Ma J, Sprott J C 2017 Chaos, Solitons Fractals 105 150 Google Scholar
[24]	Guevara M R, Glass L, Mackey M C, Shrier A 1983 IEEE Trans. Syst. Man Cybern. Syst. 5 790 Google Scholar
[25]	Chua L 2018 Appl. Phys. A: Mater. 124 563 Google Scholar
[26]	Chua L 2005 Int. J. Bifurcat. Chaos 15 3435 Google Scholar
[27]	Ascoli A, Slesazeck S, Mähne H, Tetzlaff R, Mikolajick T 2015 IEEE Trans. Circuits Syst. I Regul. Pap. 62 1165 Google Scholar
[28]	Chua L 2015 Radioengineering 24 319 Google Scholar
[29]	Wang M J, Li J H, Yu S S, Zhang X N, Li Z J, Iu H H C 2020 Chaos 30 043125 Google Scholar
[30]	Bi Q S, Gou J T 2023 Chaos Solitons Fractals 167 113046 Google Scholar
[31]	莱维坦 I B, 卡茨玛克 L K著 (舒斯云, 包新民译) 2001 神经元: 细胞和分子生物学 (北京: 科学出版社) 第43—44页 Levitan I B, Kaczmarek L K (translated by Shu S Y, Bao X M) 2001 The Neuron: Cell and Molecular Biology (Beijing: Science Press) pp43–44
[32]	Jokar E, Abolfathi H, Ahmadi A, Ahmadi M 2019 IEEE Trans. Circuits Syst. I Regul. Pap. 66 2336 Google Scholar
[33]	Li K X, Bao H, Li H Z, Ma J, Hua Z Y, Bao B C 2021 IEEE Trans. Industr. Inform. 18 1726 Google Scholar
[34]	Lin H R, Wang C H, Chen C J, Sun Y C, Zhou C, Xu C, Hong Q H 2021 IEEE Trans. Circuits Syst. I Regul. Pap. 68 3397 Google Scholar

施引文献

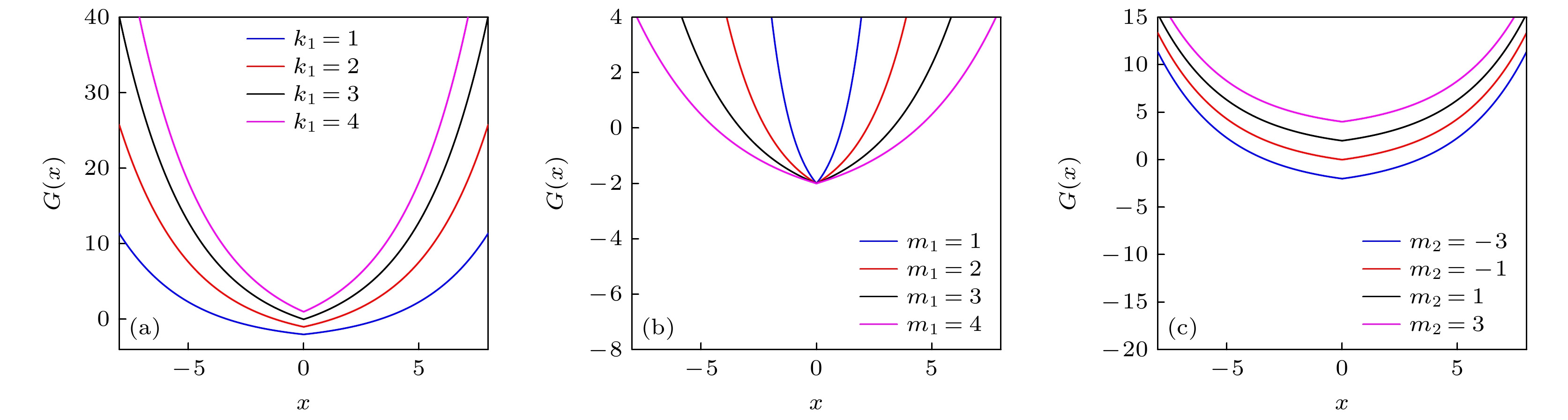
图 1 G(x)与k₁, m₁, m₂之间的关系图　(a) m₁ = 3, m₂ = –3时, k₁与G(x)之间的关系图; (b) k₁ = 1, m₂ = –3时, m₁与G(x)之间的关系图; (c) k₁ = 1, m₁ = 3时, m₂与G(x)之间的关系图

Fig. 1. Relationship between G(x) and k₁, m₁ and m₂: (a) Relationship between k₁ and G(x) when m₁ = 3 and m₂ = –3; (b) the relationship between m₁ and G(x) when k₁ = 1 and m₂ = –3; (c) the relationship between m₂ and G(x) when k₁ = 1 and m₁ = 3.

下载: 全尺寸图片幻灯片

图 2 忆阻器的滞回曲线和时域波形　(a) 不同幅值下的迟滞回线; (b) 不同频率下的迟滞回线; (c) 电压和电流的时域波形

Fig. 2. Hysteresis curves and time domain waveforms of memristor: (a) Hysteresis curves at different amplitudes; (b) hysteresis curves at different frequencies; (c) time domain waveforms of voltage and current.

下载: 全尺寸图片幻灯片

图 3 忆阻器的POP (a)和DC V-I图(b)

Fig. 3. POP (a) and DC V-I (b) diagram of the memristor.

下载: 全尺寸图片幻灯片

图 4 忆阻耦合的HNN的拓扑结构图

Fig. 4. Topological structure diagram of memristor coupled HNN.

下载: 全尺寸图片幻灯片

图 5 不同初始值下系统关于m₁的分岔图　(a) (–2, 1, 1, 1, 6); (b) (–2, 1, 1, 1, 6.5); (c) (–2, 1, 1, 1, 8)

Fig. 5. Bifurcation diagram of the system about m₁ under different initial values: (a) (–2, 1, 1, 1, 6); (b) (–2, 1, 1, 1, 6.5); (c) (–2, 1, 1, 1, 8).

下载: 全尺寸图片幻灯片

图 6 x₁-x₃平面共存非对称吸引子相图　(a) m₁ = 0.01; (b) m₁ = 0.05; (c) m₁ = 0.1; (d) m₁ = 0.83; (e) m₁ = 1.13; (f) m₁ = 2.5

Fig. 6. Coexistence asymmetric attractor phase diagram of the x₁-x₃ plane: (a) m₁ = 0.01; (b) m₁ = 0.05; (c) m₁ = 0.1, (d) m₁ = 0.83; (e) m₁ = 1.13; (f) m₁ = 2.5.

下载: 全尺寸图片幻灯片

图 7 系统的共存分岔图以及x₁-x₃平面共存对称吸引子相图　(a) 系统的共存分岔图; (b) m₁ = 0.01; (c) m₁ = 0.1

Fig. 7. Coexistence bifurcation diagram of the system and the coexistence symmetric attractor phase diagram of the x₁-x₃ plane: (a) Coexistence bifurcation diagram of the system; (b) m₁ = 0.01; (c) m₁ = 0.1.

下载: 全尺寸图片幻灯片

图 8 系统关于m₂的分岔图(a)及李雅普诺夫指数谱(b)

Fig. 8. Bifurcation diagram (a) and Lyapunov exponent spectrum (b) of the system about m₂.

下载: 全尺寸图片幻灯片

图 9 系统关于f的分岔图

Fig. 9. Bifurcation diagram of the system about f.

下载: 全尺寸图片幻灯片

图 10 不同频率下系统的相轨图(a), (c)和时域波形图(b), (d)　(a), (b) f = 0.003; (c), (d) f = 0.1

Fig. 10. Phase diagram (a), (c) and time domain waveform diagram (b), (d) of the system at different frequencies: (a), (b) f = 0.003; (c), (d) f = 0.1.

下载: 全尺寸图片幻灯片

图 11 系统的实物连接图

Fig. 11. Physical connection diagram of the system.

下载: 全尺寸图片幻灯片

图 12 用STM32实现ODE45算法的流程图

Fig. 12. Flow chart of ODE45 algorithm implemented by STM32.

下载: 全尺寸图片幻灯片

图 13 示波器显示的相轨图(a)—(c)及对应Matlab仿真图(d)—(f)　(a), (d) m₁ = 0.02; (b), (e) m₁ = 1.2; (c), (f) m₁ = 2.5

Fig. 13. Oscilloscope display phase track diagram (a)–(c) and the corresponding Matlab simulation diagram (d)–(f): (a), (d) m₁ = 0.02; (b), (e) m₁ = 1.2; (c), (f) m₁ = 2.5.

下载: 全尺寸图片幻灯片

表 1 a = 2.5, m₁ = 0.5, m₂ = –3时, 系统平衡点处的特征值及稳定性

Table 1. Eigenvalue and stability at the equilibrium point of the system when a = 2.5, m₁ = 0.5 and m₂ = –3.

m₁	k	特征值	稳定性
0.5	0	1, 1.0399, –3.7032, 0.7316±3.9891i	不稳定的鞍焦点
	±1	–1, 1.4681±2.5644i, –2.0681±40.1411i	不稳定的鞍焦点
	±2	1, 1.4833±2.5761i, –2.0833±927.5014i	不稳定的鞍焦点
	±3	–1, 1.4833±2.5761i, –2.0833±21462.9637i	不稳定的鞍焦点

下载: 导出CSV

表 2 不同的忆阻耦合Hopfield神经网络

Table 2. Different memristor-coupled Hopfield neural networks.

系统	维度	局部有源忆阻器	G(x)的类型	共存现象	宽参数范围混沌状态
文献[12]	三维	无	一次函数	有	无
文献[14]	四维	无	双曲正切函数	有	无
文献[15]	四维	有	二次函数	有	无
文献[16]	二维	无	余弦函数	有	无
文献[17]	四维	有	绝对值函数	有	无
本文	五维	有	复合指数函数	有	有

下载: 导出CSV

map

[1]	Chua L 1971 IEEE Trans. Circuits Syst. I Regul. Pap. 18 507 Google Scholar
[2]	Chua L 2014 Semicond. Sci. Technol. 29 104001 Google Scholar
[3]	Wang M J, Deng Y, Liao X H, Li Z J, Ma M L, Zeng Y C 2019 Int. J. Non. Linear. Mech. 111 149 Google Scholar
[4]	Peng Y X, Liu J, He S B, Sun K H 2023 Chaos, Solitons Fractals 171 113429 Google Scholar
[5]	Wang M J, An M Y, He S B, Zhang X N, Iu H H, Li Z J 2023 Chaos 33 073129 Google Scholar
[6]	Peng Y X, He S B, Sun K H 2022 Nonlinear Dyn. 107 1263 Google Scholar
[7]	He S B, Liu J, Wang H H, Sun K H 2023 Neurocomputing (Amst. ) 523 1 Google Scholar
[8]	古亚娜, 梁燕, 王光义, 夏晨阳 2022 71 110501 Google Scholar Gu Y N, Liang Y, Wang G Y, Xia C Y 2022 Acta Phys. Sin. 71 110501 Google Scholar
[9]	武长春, 周莆钧, 王俊杰, 李国, 胡绍刚, 于奇, 刘洋 2022 71 148401 Google Scholar Wu C C, Zhou P J, Wang J J, Li G, Hu S G, Yu Q, Liu Y 2022 Acta Phys. Sin. 71 148401 Google Scholar
[10]	Chua L 2013 Nanotechnology 24 383001 Google Scholar
[11]	Lu Y C, Li H M, Li C L 2023 Neurocomputing (Amst. ) 544 126246 Google Scholar
[12]	Li Z J, Chen K J 2023 Chaos, Solitons Fractals 175 114017 Google Scholar
[13]	Hopfield J J 1984 Proc. Natl. Acad. Sci. U. S. A. 81 3088 Google Scholar
[14]	Chen C J, Chen J Q, Bao H, Chen M, Bao B C 2019 Nonlinear Dyn. 95 3385 Google Scholar
[15]	Lin H R, Wang C H, Hong Q H, Sun Y C 2020 IEEE Tran. Circuits Syst. II Express Briefs 67 3472 Google Scholar
[16]	Chen C J, Min F H, Zhang Y Z, Bao B C 2021 Nonlinear Dyn. 106 2559 Google Scholar
[17]	Li C L, Yang Y Y, Yang X B, Zi X Y, Xiao F L 2022 Nonlinear Dyn. 108 1697 Google Scholar
[18]	Doubla I S, Ramakrishnan B, Njitacke Z T, Kengne J, Rajagopal K 2022 Int. J. Electron. Commun. 144 154059 Google Scholar
[19]	黄丽丽, 黄强, 黄振, 臧红岩, 雷腾飞 2023 电子元件与材料 42 10 Google Scholar Huang L L, Huang Q, Huang Z, Zang H Y, Lei T F 2023 Electron. Compon. Mater. 42 10 Google Scholar
[20]	Lin H R, Wang C H, Sun J R, Zhang X, Sun Y C, Iu H H C 2023 Chaos Solitons Fractals 166 112905 Google Scholar
[21]	Wan Q Z, Chen S M, Yang Q, Liu J, Sun K L 2023 Nonlinear Dyn. 111 18505 Google Scholar
[22]	Lin H R, Wang C H, Yu F, Sun J R, Du S C, Deng Z K, Deng Q L 2023 Mathematics (Basel) 11 1369 Google Scholar
[23]	Panahi S, Aram Z, Jafari S, Ma J, Sprott J C 2017 Chaos, Solitons Fractals 105 150 Google Scholar
[24]	Guevara M R, Glass L, Mackey M C, Shrier A 1983 IEEE Trans. Syst. Man Cybern. Syst. 5 790 Google Scholar
[25]	Chua L 2018 Appl. Phys. A: Mater. 124 563 Google Scholar
[26]	Chua L 2005 Int. J. Bifurcat. Chaos 15 3435 Google Scholar
[27]	Ascoli A, Slesazeck S, Mähne H, Tetzlaff R, Mikolajick T 2015 IEEE Trans. Circuits Syst. I Regul. Pap. 62 1165 Google Scholar
[28]	Chua L 2015 Radioengineering 24 319 Google Scholar
[29]	Wang M J, Li J H, Yu S S, Zhang X N, Li Z J, Iu H H C 2020 Chaos 30 043125 Google Scholar
[30]	Bi Q S, Gou J T 2023 Chaos Solitons Fractals 167 113046 Google Scholar
[31]	莱维坦 I B, 卡茨玛克 L K著 (舒斯云, 包新民译) 2001 神经元: 细胞和分子生物学 (北京: 科学出版社) 第43—44页 Levitan I B, Kaczmarek L K (translated by Shu S Y, Bao X M) 2001 The Neuron: Cell and Molecular Biology (Beijing: Science Press) pp43–44
[32]	Jokar E, Abolfathi H, Ahmadi A, Ahmadi M 2019 IEEE Trans. Circuits Syst. I Regul. Pap. 66 2336 Google Scholar
[33]	Li K X, Bao H, Li H Z, Ma J, Hua Z Y, Bao B C 2021 IEEE Trans. Industr. Inform. 18 1726 Google Scholar
[34]	Lin H R, Wang C H, Chen C J, Sun Y C, Zhou C, Xu C, Hong Q H 2021 IEEE Trans. Circuits Syst. I Regul. Pap. 68 3397 Google Scholar

计量

文章访问数: 3655
PDF下载量: 105
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板