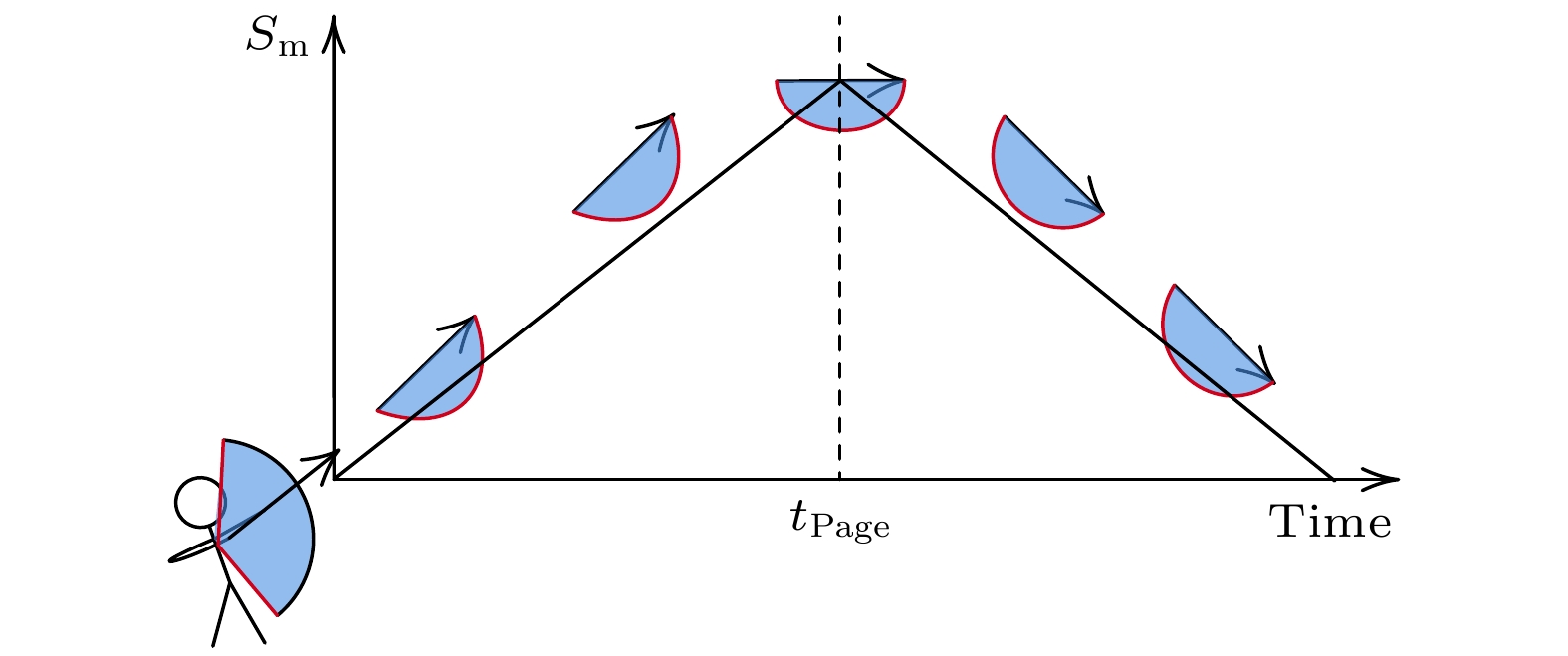
-
The black hole information paradox—a fundamental conflict between quantum unitarity and semi-classical gravity—remains unresolved within the framework of quantum gravity. This work builds a conceptual bridge between this modern dilemma and Zeno’s ancient paradox of motion, emphasizing that they all rely on limit processes to reconcile infinite divisibility with finite physical outcomes. Although previous researches have established information conservation in black hole evaporation by copying wormholes, this study transcends mere unitarity verification to answer a deeper question: How do we quantify the statistical evolution and inherent irreversibility of Hawking radiation? Methods : i) Gravitational path integral formalism : We compute Rényi entropies $ S_n = \dfrac{1}{1-n} \ln \text{Tr}(\rho^n) $ by analytic continuation $( n \to 1 )$, incorporating both disconnected geometries (Hawking saddles) and connected replica wormhole saddles. ii) JT gravity model : A two-dimensional Jackiw-Teitelboim (JT) gravity coupled to a conformal bath is analyzed, with End-of-the-World (EOW) branes modeling early Hawking radiation states. iii) Modular thermodynamics : Modular entropy $ S_m $ and entanglement capacity $ C_n $ are defined as: $ S_m = \log\text{Tr}(\rho^n) - n\partial_n\log\text{Tr}(\rho^n), \quad C_n = n^2\partial_n^2\log\text{Tr}(\rho^n),$mirroring thermodynamic entropy and heat capacity. Key results : i) Page curve restoration : The von Neumann entropy transitions from linear growth (Hawking phase) to zero (wormhole-dominated phase) at the Page time: $ t_{\text{Page}} \propto {S_{\text{BH}}}/({n\kappa c}), \quad S_{\text{BH}} = {A}/({4G_N}), $indicating faster entropy reduction for higher n. ii) Replica wormhole mechanism : The gravitational path integral reveals a topological transition: $ \text{Tr}(\rho^n) \approx \dfrac{kZ_1^n + k^n Z_n}{(kZ_1)^n} \quad \Rightarrow \quad \text{Dominance shift at } k \sim {\mathrm{e}}^{S_0}$. Quantum non-cloning constraints: A reversibility paradox arises: while n-copies -copies of a known state allow full reconstruction, the non-cloning theorem forbids replication of unknown states. This necessitates the a priori existence of multiple replicas to ensure consistency. iii) Connection to Zeno’s paradox : The resolution of Zeno’s paradox through Newtonian limits $( v = \lim\limits_{\Delta t \to 0} \Delta x / \Delta t $) parall) parallels the replica trick’s role in black hole physics: iv) Infinite-to-finite mapping : Both employ limit operations to compress divergent processes (infinite steps or entropy growth) into finite observables. Discrete vs. continuous : Challenge classical spacetime continuity, hinting at holographic or discrete quantum spacetime. Irreversibility and generalized second law : The relative entropy $ S(\rho \| \sigma) $, defined as: $ S(\rho \| \sigma) = \text{Tr}(\rho \log \rho) - \text{Tr}(\rho \log \sigma),$monotonically increases during the Hawking-to-wormhole transition, establishing statistical irreversibility in modular space. This generalized second law persists despite microscopic unitarity, analogous to thermodynamic irreversibility in closed systems with the formula: $ \left(S_n-S_{\rho}\right)-n\left(\left\langle H\right\rangle_n-\left\langle H\right\rangle_{\rho}\right)\geqslant 0 $. Conclusion : Our results address the black hole information paradox and the irreversible problem through three pillars: i) Unitarity : Replica wormholes enforce unitarity via non-perturbative spacetime topology changes. ii) Modular thermodynamics : A framework linking entanglement entropy, relative entropy, and irreversibility. iii) Replica priority principle : Multiple radiation replicas exist a priori, circumventing quantum cloning constraints. This work transcends mere information conservation, advancing into the second layer of black hole physics: Characterizing the irreversible evolution of Hawking radiation in modular space. 
-
Keywords:
- gravity/gauge duality /
- von Neumann entropy /
- Rényi entropy /
- replica trick /
- quantum non-cloning theorem /
- generalized second law of thermodynamics via relative entropy
[1] Hawking S W 1975 Commun. Math. Phys. 43 199
Google Scholar
[2] Hawking S W 1976 Phys. Rev. D 14 2460
Google Scholar
[3] Susskind L, Thorlacius J 1993 Phys. Rev. D 48 3743
Google Scholar
[4] Susskind L, Thorlacius J 1994 Phys. Rev. D 49 966
Google Scholar
[5] Maldacena J 1999 Int. J. Theor. Phys. 38 1113
Google Scholar
[6] Hartman T, Shaghoulian E, Strominger A 2020 J. High Energy. Phys. 07 022
Google Scholar
[7] Hashimoto K, Iizuka N, Matsuo Y 2020 J. High Energy. Phys. 06 085
Google Scholar
[8] Wang X, Li R, Wang J 2021 J. High Energy. Phys. 04 103
[9] Kim W, Nam M 2021 Eur. Phys. J. C 81 869
Google Scholar
[10] Ling Y, Liu Y, Xian Z Y 2021 J. High Energy. Phys. 03 251
[11] Yu M H, Ge X H 2023 Phys. Rev. D 107 066020
Google Scholar
[12] Yu M H, Ge X H 2022 Eur. Phys. J. C 82 14
Google Scholar
[13] Ge X H Ph.D Dissertation (Shanghai: Shanghai Astronomical Observatory, Chinese Academy of Sciences) [葛先辉 2006 博士论文 (上海: 中国科学院上海天文台)]
Ge X H Ph.D Dissertation (Shanghai: Shanghai Astronomical Observatory, Chinese Academy of Sciences)
[14] Ge X H, Shen Y G 2005 Phys. Lett. B 612 61
Google Scholar
[15] Ge X H, Shen Y G 2005 Int. J. Mod. Phys. D 14 1321
Google Scholar
[16] Ge X H, Shen Y G 2004 Class. Quant. Grav. 21 1941
Google Scholar
[17] Ge X H, Shen Y G 2004 Chin. Phys. Lett. 21 1413
Google Scholar
[18] Page D N 1993 Phys. Rev. Lett. 71 3743
Google Scholar
[19] Page D N 2013 JCAP 1309 028
[20] Page D N 1993 Phys. Rev. Lett. 71 1291
Google Scholar
[21] Lewkowycz A, Maldacena J 2013 J. High Energy. Phys. 08 090
Google Scholar
[22] Engelhardt N, Wall A 2015 J. High Energy. Phys. 01 073
Google Scholar
[23] Almheiri A, Engelhardt N, Marolf D, Maxfield H 2019 J. High Energy. Phys. 12 063
Google Scholar
[24] Almheiri A, Mahajan R, J. Maldacena J, Zhao Y 2020 J. High Energy. Phys. 03 149
Google Scholar
[25] Penington G 2020 J. High Energy. Phys. 09 002
Google Scholar
[26] Almheiri A, Hartman T, Maldacena J, Shaghoulian E, Tajdini A 2021 Rev. Mod. Phys. 93 035002
Google Scholar
[27] Almheiri A, Mahajan R, Maldacena J 2019 arXiv: 1910.11077 [hep-th]
[28] Hollowood T, Kumar S 2020 J. High Energy. Phys. 08 094
Google Scholar
[29] Goto K, Hartman T, Tajdini A 2021 J. High Energy. Phys. 04 289
Google Scholar
[30] Miao R 2024 Eur. Phys. J. C 84 84
Google Scholar
[31] Chu J W, Deng F Y, Zhou Y 2021 J. High Energy. Phys. 10 149
Google Scholar
[32] Chen Y M, Qi X L, Zhang P 2020 J. High Energy. Phys. 06 121
Google Scholar
[33] Du D H, Gan W C, Shu F W, Sun J R 2023 Phys. Rev. D 107 026005
Google Scholar
[34] Ling Y, Liu P, Liu Y X, Niu C, Xian Z Y, Zhang C Y 2022 J. High Energy. Phys. 02 037
Google Scholar
[35] Penington G, Shenker S H, Stanford D, Yang Z B 2022 J. High Energy. Phys. 03 205
Google Scholar
[36] Almheiri A, Hartman T, Maldacena J, Shaghoulian E, Tajdini A 2020 J. High Energy. Phys. 05 013
Google Scholar
[37] Wotters W K, Zurek W H 1982 Nature 299 802
Google Scholar
[38] Rangamania R, Takayanagi T 2016 Lect. Notes Phys. 931 1
Google Scholar
[39] Nakaguchia Y, Nishiokab T 2016 J. High Energy. Phys. 12 129
Google Scholar
[40] Dong X 2016 Nat. Commun. 7 12472
Google Scholar
[41] Casini H 2008 Class. Quant. Grav. 25 205021
Google Scholar
-
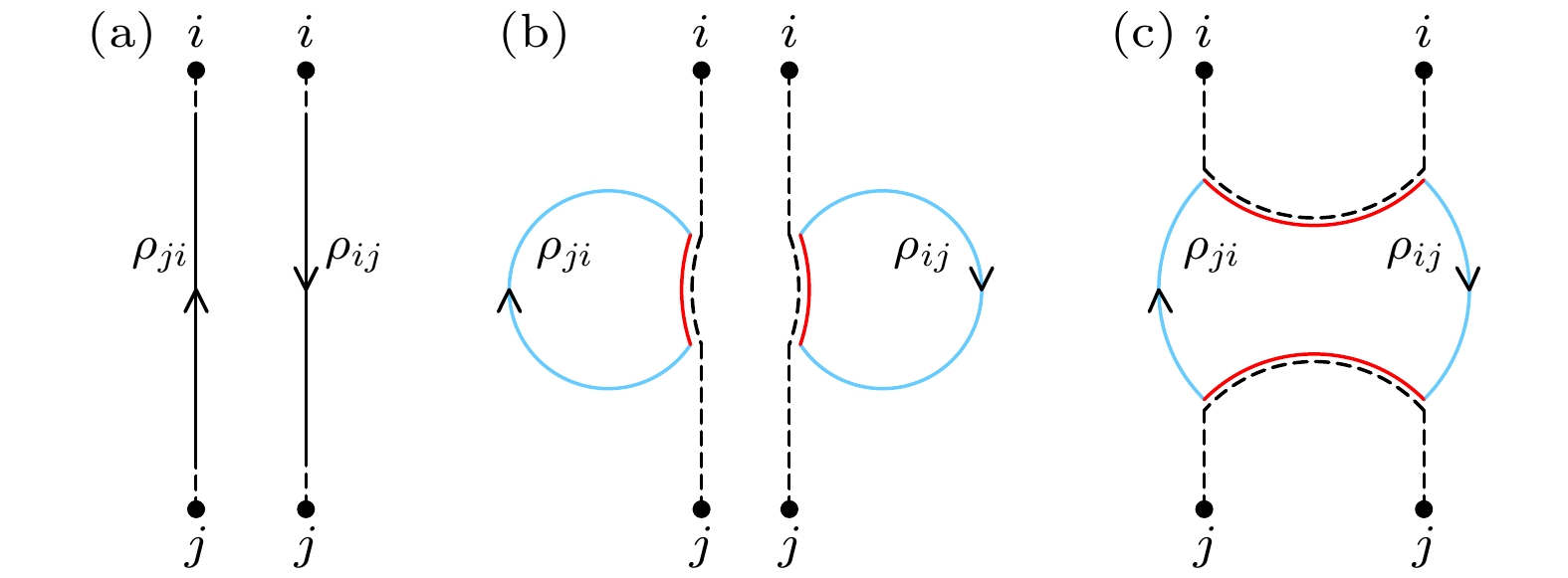
图 1 引力路径积分示意图. 指标i和j代表不同的态. 引力区域用蓝色显示; EOW用红色显示 (a)$ |\langle \psi_i|\psi_j\rangle|^2 $的边界条件； (b)和(c)分别为两种填充方式
Figure 1. Schematic diagram for the gravitational path integral. The indices i and j represent different states. The gravitational region is shown in blue and the EOW brane is shown in red: (a) The bodunary conditions for $ |\langle \psi_i|\psi_j\rangle|^2 $; (b) and (c) are two different filling ways.
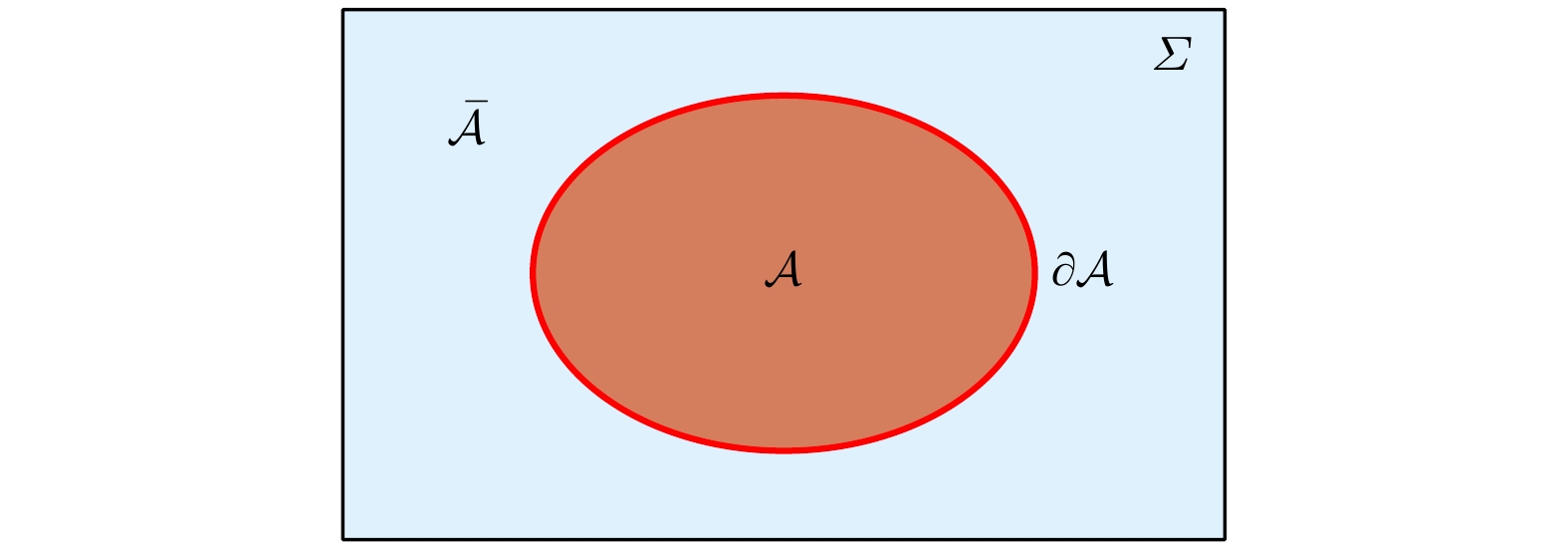
图 2 纠缠熵的示意图. 在一个连续的量子场论(QFT)中, 柯西面(Cauchy slice) Σ被空间划分为两个区域. 标记$ A $其中一个区域为$ {\cal{A}}$, 补集为$ \bar{\cal{A}} = \varSigma/{\cal{A}} $. 这两个区域之间的分界是一个余维数为2的曲面, 称为纠缠面
Figure 2. The entanglement entropy in QFT, A Cauchy slice Σ is divided into two regions. The region $ {\cal{A}} $ and its complementary $ \bar{\cal{A}}= \varSigma/{\cal{A}} $. The boundary between these two regions is a surface with a codimension of 2, called the entangling surface.
表 1 统计力学量与模空间物理量的类比
Table 1. Analogy between statistical mechanical quantities and physical quantities in modular space
统计力学量 表达式 Modular类比 表达式 逆温度 β 副本参数 n 哈密顿量 H 模哈密顿量 ${\cal{H}}=-\log {\boldsymbol{\rho}}_A$ 配分函数 $Z(\beta)={\mathrm{Tr}}({\mathrm{e}}^{-\beta H})$ 副本配分函数 $Z_n(n)={\mathrm{Tr}}({\mathrm{e}}^{-n {\cal{H}}_A})$ 自由能 $F(\beta)=-\dfrac{1}{\beta}\log {\mathrm{Tr}}[{\mathrm{e}}^{-\beta H}]$ 副本自由能 $F(n)= -\dfrac{1}{n}\log [{\mathrm{Tr}}_A {\boldsymbol{\rho}}^n_{A}]$ 能量 $E(\beta)=\langle H \rangle=-\partial_{\beta} \log[{\mathrm{Tr\, e}}^{-\beta H}]$ 副本能量 $E(n)=-\partial_n \log [{\mathrm{Tr}} {\boldsymbol{\rho}}^n_A]$ 热力学熵 $S(\beta)=\log[{\mathrm{Tr \,e}}^{-\beta H}]-\beta \partial_{\beta}\log[{\mathrm{Tr \,e}}^{-\beta H}]$ 模熵 $S_m= \log[{\mathrm{Tr}} {\boldsymbol{\rho}}^n_A]-n \partial_n \log[{\mathrm{Tr}} {\boldsymbol{\rho}}^n_A]$ 热容量 $C(\beta)=\beta^2 \partial^2_{\beta}\log[{\mathrm{Tr \,e}}^{-\beta H}]$ 纠缠容量 $C_n=n^2 \partial^2_n \log[{\mathrm{Tr}} {\boldsymbol{\rho}}^n_A]$ 
DownLoad: CSV
-
[1] Hawking S W 1975 Commun. Math. Phys. 43 199
Google Scholar
[2] Hawking S W 1976 Phys. Rev. D 14 2460
Google Scholar
[3] Susskind L, Thorlacius J 1993 Phys. Rev. D 48 3743
Google Scholar
[4] Susskind L, Thorlacius J 1994 Phys. Rev. D 49 966
Google Scholar
[5] Maldacena J 1999 Int. J. Theor. Phys. 38 1113
Google Scholar
[6] Hartman T, Shaghoulian E, Strominger A 2020 J. High Energy. Phys. 07 022
Google Scholar
[7] Hashimoto K, Iizuka N, Matsuo Y 2020 J. High Energy. Phys. 06 085
Google Scholar
[8] Wang X, Li R, Wang J 2021 J. High Energy. Phys. 04 103
[9] Kim W, Nam M 2021 Eur. Phys. J. C 81 869
Google Scholar
[10] Ling Y, Liu Y, Xian Z Y 2021 J. High Energy. Phys. 03 251
[11] Yu M H, Ge X H 2023 Phys. Rev. D 107 066020
Google Scholar
[12] Yu M H, Ge X H 2022 Eur. Phys. J. C 82 14
Google Scholar
[13] Ge X H Ph.D Dissertation (Shanghai: Shanghai Astronomical Observatory, Chinese Academy of Sciences) [葛先辉 2006 博士论文 (上海: 中国科学院上海天文台)]
Ge X H Ph.D Dissertation (Shanghai: Shanghai Astronomical Observatory, Chinese Academy of Sciences)
[14] Ge X H, Shen Y G 2005 Phys. Lett. B 612 61
Google Scholar
[15] Ge X H, Shen Y G 2005 Int. J. Mod. Phys. D 14 1321
Google Scholar
[16] Ge X H, Shen Y G 2004 Class. Quant. Grav. 21 1941
Google Scholar
[17] Ge X H, Shen Y G 2004 Chin. Phys. Lett. 21 1413
Google Scholar
[18] Page D N 1993 Phys. Rev. Lett. 71 3743
Google Scholar
[19] Page D N 2013 JCAP 1309 028
[20] Page D N 1993 Phys. Rev. Lett. 71 1291
Google Scholar
[21] Lewkowycz A, Maldacena J 2013 J. High Energy. Phys. 08 090
Google Scholar
[22] Engelhardt N, Wall A 2015 J. High Energy. Phys. 01 073
Google Scholar
[23] Almheiri A, Engelhardt N, Marolf D, Maxfield H 2019 J. High Energy. Phys. 12 063
Google Scholar
[24] Almheiri A, Mahajan R, J. Maldacena J, Zhao Y 2020 J. High Energy. Phys. 03 149
Google Scholar
[25] Penington G 2020 J. High Energy. Phys. 09 002
Google Scholar
[26] Almheiri A, Hartman T, Maldacena J, Shaghoulian E, Tajdini A 2021 Rev. Mod. Phys. 93 035002
Google Scholar
[27] Almheiri A, Mahajan R, Maldacena J 2019 arXiv: 1910.11077 [hep-th]
[28] Hollowood T, Kumar S 2020 J. High Energy. Phys. 08 094
Google Scholar
[29] Goto K, Hartman T, Tajdini A 2021 J. High Energy. Phys. 04 289
Google Scholar
[30] Miao R 2024 Eur. Phys. J. C 84 84
Google Scholar
[31] Chu J W, Deng F Y, Zhou Y 2021 J. High Energy. Phys. 10 149
Google Scholar
[32] Chen Y M, Qi X L, Zhang P 2020 J. High Energy. Phys. 06 121
Google Scholar
[33] Du D H, Gan W C, Shu F W, Sun J R 2023 Phys. Rev. D 107 026005
Google Scholar
[34] Ling Y, Liu P, Liu Y X, Niu C, Xian Z Y, Zhang C Y 2022 J. High Energy. Phys. 02 037
Google Scholar
[35] Penington G, Shenker S H, Stanford D, Yang Z B 2022 J. High Energy. Phys. 03 205
Google Scholar
[36] Almheiri A, Hartman T, Maldacena J, Shaghoulian E, Tajdini A 2020 J. High Energy. Phys. 05 013
Google Scholar
[37] Wotters W K, Zurek W H 1982 Nature 299 802
Google Scholar
[38] Rangamania R, Takayanagi T 2016 Lect. Notes Phys. 931 1
Google Scholar
[39] Nakaguchia Y, Nishiokab T 2016 J. High Energy. Phys. 12 129
Google Scholar
[40] Dong X 2016 Nat. Commun. 7 12472
Google Scholar
[41] Casini H 2008 Class. Quant. Grav. 25 205021
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 445
- PDF Downloads: 17
- Cited By: 0
