Electron transmission dynamics of Ge1–x Snx alloys based on inter-valley electrons transferring effect

HUANG Shihao; LI Jiapeng; LI Hailin; LU Xuxing; SUN Qinqin; XIE Deng

doi:10.7498/aps.74.20240980

Abstract

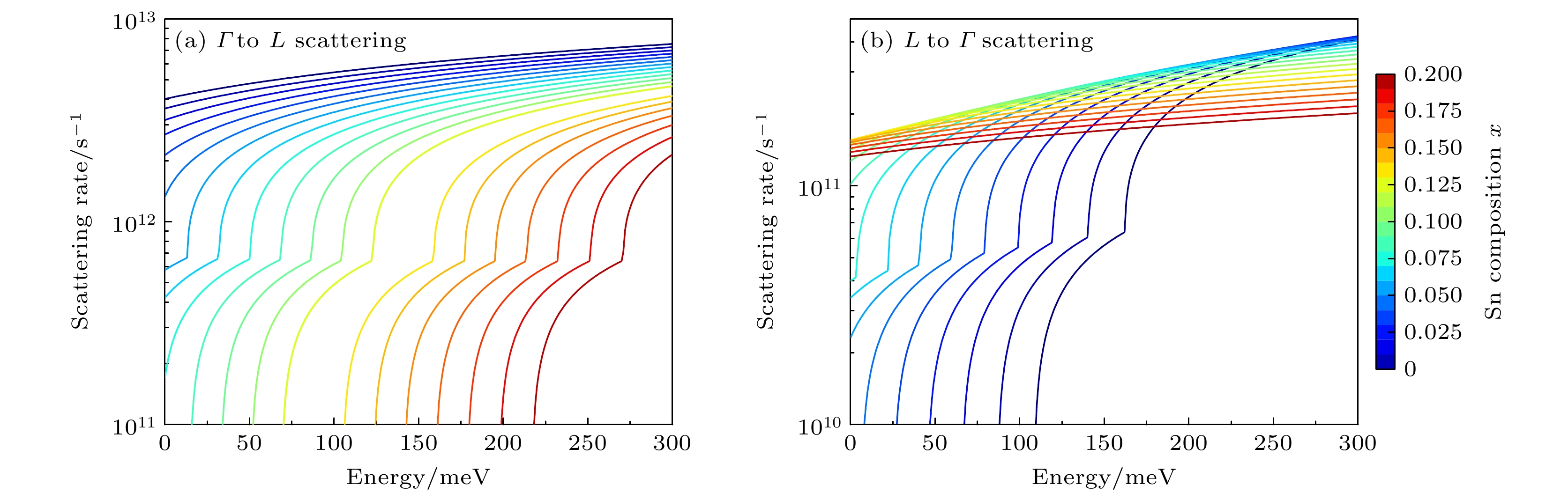
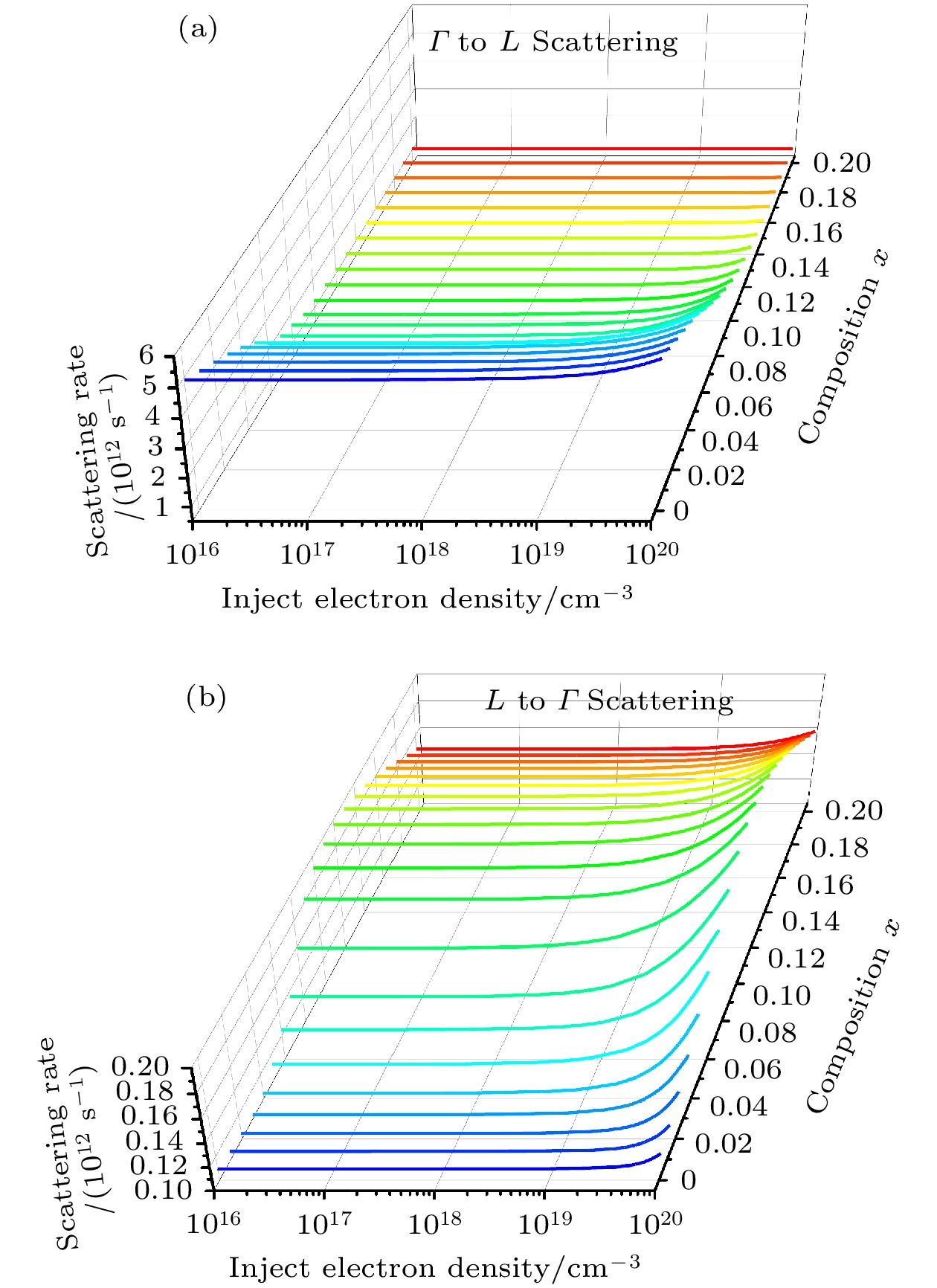
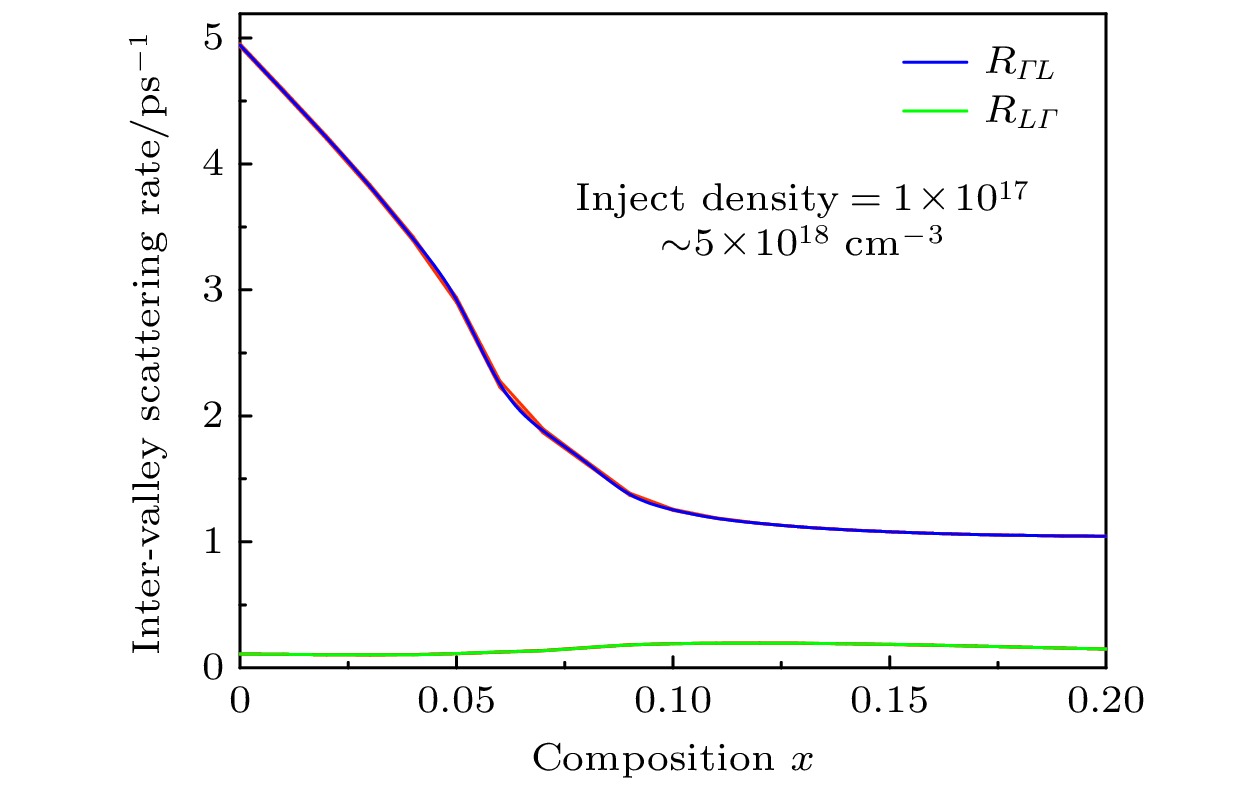
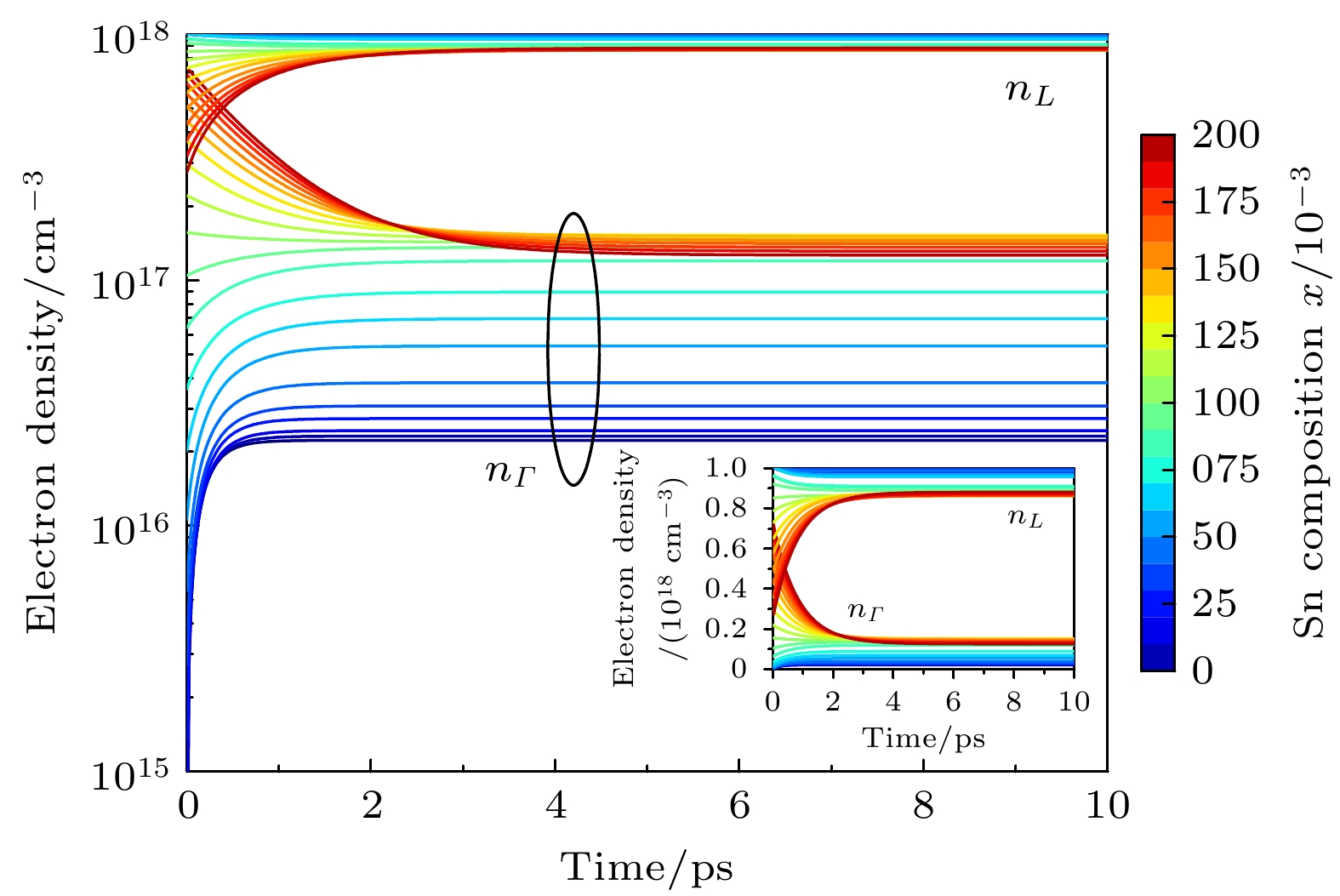
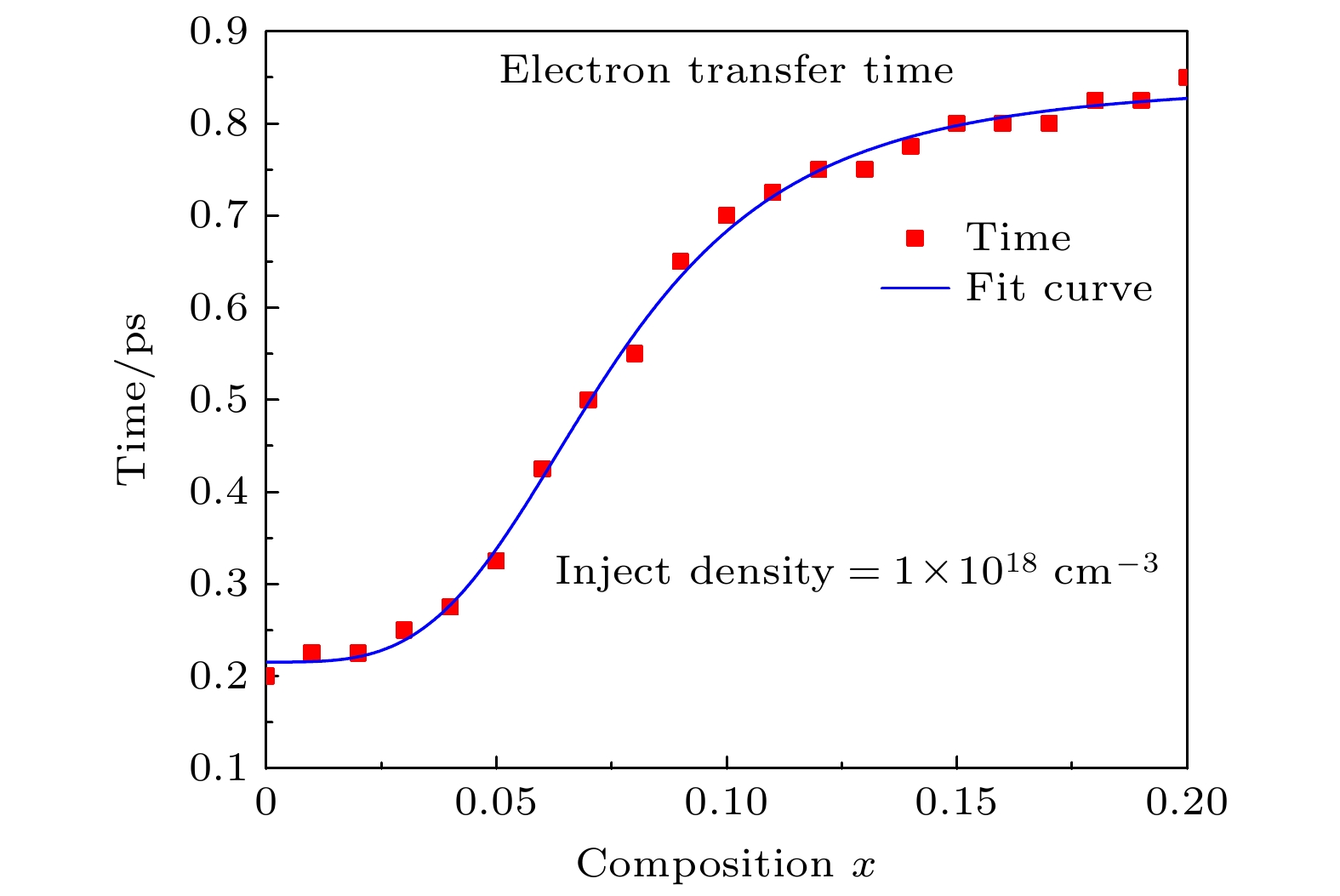
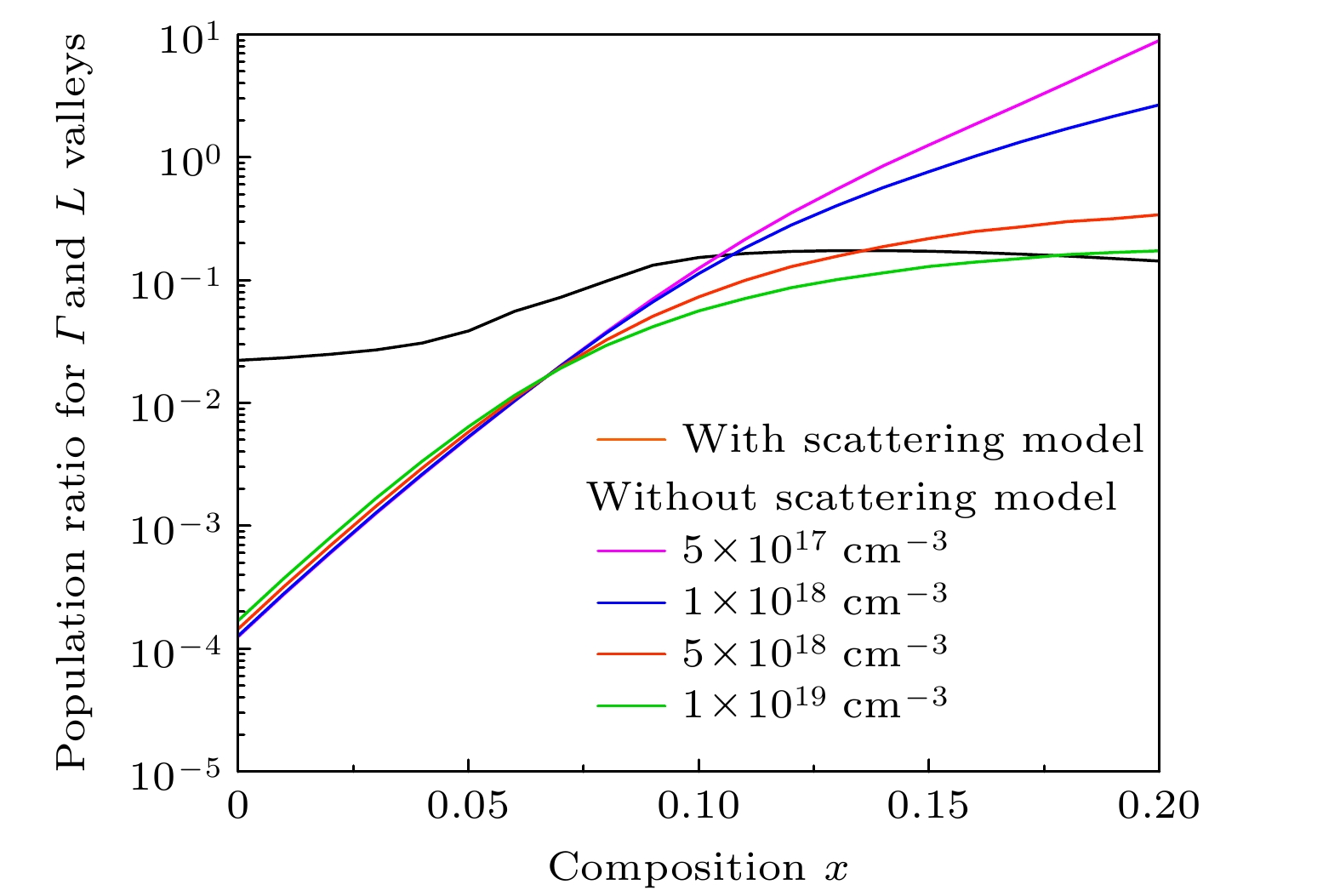
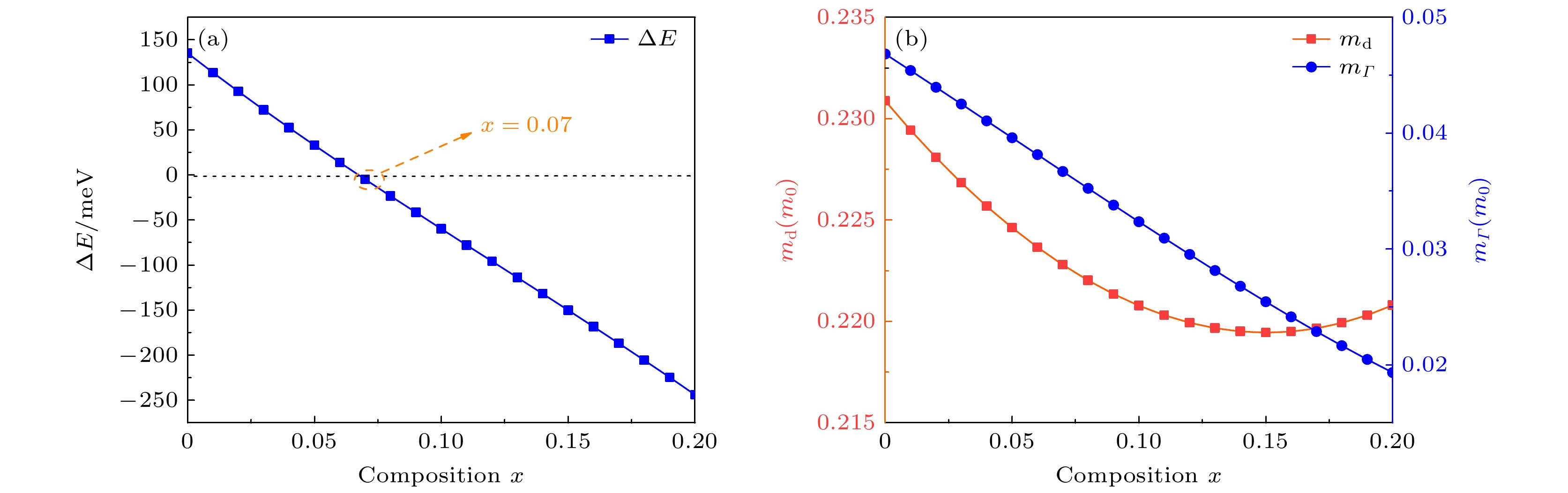
Ge_1–x Sn_x alloys have aroused great interest in silicon photonics because of their compatiblity with complementary metal-oxide-semiconductor (CMOS) technology. As a result, they are considered potential candidate materials. Owing to the significant differences in effective mass within the valleys, the unique dual-valley structure of Γ valley and L valley in energy can improve the optoelectronic properties of Ge_1–x Sn_x alloys. Therefore, inter-valley scattering mechanisms between the Γ and L valley in Ge_1–x Sn_x alloys are crucial for understanding the electronic transports and optical properties of Ge_1–x Sn_x materials. This work focuses on the theoretical analysis of inter-valley scattering mechanisms between Γ and L valley, and hence on the electron transmission dynamics in Ge_1–x Sn_x alloys based on the phenomenological theory model.Firstly, the 30th-order k ·p perturbation theory is introduced to reproduce the band structure of Ge_1–x Sn_x. The results show that the effective mass of L valley is always about an order of magnitude higher than that of Γ valley, which will significantly influence the electron distributions between Γ and L valley.Secondly, the scattering mechanism is modeled in Ge_1–x Sn_x alloys. The results indicate that scattering rate R_ΓL is about an order of magnitude higher than R_LΓ, while R_ΓL decreases with the increase of Sn composition and tends to saturate when Sn component is greater than 0.1. And R_LΓ is almost independent of the Sn component.Thirdly, kinetic processes of carriers between Γ and L valley are proposed to analyze the electron transmission dynamics in Ge_1–x Sn_x alloys. Numerical results indicate that the electron population ratio for Γ-valley increases and then tends to saturation with the increase of Sn composition, and is independent of the injected electron concentration. The model without the scattering mechanism indicates that the electron population ratio for Γ-valley in indirect-Ge_1–x Sn_x alloys is independent of the injected electron concentration, while the electron population ratio for Γ-valley in direct-Ge_1–x Sn_x alloys is dependent on the injected electron concentration, and the lower the electron concentration, the greater the electron population ratio for Γ-valley is.The results open a new way of understanding the mechanisms of electron mobility, electrical transport, and photoelectric conversion in Ge_1–x Sn_x alloys, and can provide theoretical value for designing Ge_1–x Sn_x alloys in the fields of microelectronics and optoelectronics.

Keywords:

Authors and contacts

School of Electronic, Electrical Engineering and Physics, Fujian University of Technology, Fuzhou 350118, China

Corresponding author: HUANG Shihao, haoshihuang@fjut.edu.cn

Funds: Project supported by the Natural Science Foundation of Fujian Province, China (Grant No. 2022J01950).

FullText HTML

References

[1]	Miao Y H, Wang G L, Kong Z Z, Xu B Q, Zhao X W, Luo X, Lin H X, Dong Y, Lu B, Dong L P, Zhou J R, Liu J B, Radamson H H 2021 Nanomaterials 11 2556 Google Scholar
[2]	Oka H, Mizubayashi W, Ishikawa Y, Uchida N, Mori T, Endo K 2021 Appl. Phys. Express 14 096501 Google Scholar
[3]	Zhang D, Song J J, Xue X X, Zhang S Q 2022 Chin. Phys. B 31 068401 Google Scholar
[4]	Wang H J, Han G Q, Jiang X W, Liu Y, Zhang J C, Hao Y 2019 IEEE Trans. Electron Devices 66 1985 Google Scholar
[5]	Wang P C, Huang P R, Ghosh S, Bansal R, Jheng Y T, Lee K C, Cheng H H, Chang G E 2024 ACS Photonics 11 2659 Google Scholar
[6]	Reboud V, Concepción O, Du W, El Kurdi M, Hartmann J M, Ikonic Z, Assali S, Pauc N, Calvo V, Cardoux C, Kroemer E, Coudurier N, Rodriguez P, Yu S Q, Buca D, Chelnokov A 2024 Photon. Nanostruc. Fundam. Appl. 58 101233 Google Scholar
[7]	Zheng J, Liu Z, Xue C L, Li C B, Zuo Y H, Cheng B W, Wang Q M 2018 J. Semicond. 39 061006 Google Scholar
[8]	Zhou Y Y, Dou W, Du W, Pham T, Ghetmiri S A, Al-Kabi S, Mosleh A, Alher M, Margetis J, Tolle J, Sun G, Soref R, Li B, Mortazavi M, Naseem H, Yu S Q 2016 J. Appl. Phys. 120 023102 Google Scholar
[9]	Ghetmiri S A, Du W, Margetis J, Mosleh A, Cousar L, Conley B R, Domulevicz L, Nazzal A, Sun G, Soref R A, Tolle J, Li B, Naseem H A, Yu S Q 2014 Appl. Phys. Lett. 105 151109 Google Scholar
[10]	Wirths S, Geiger R, von den Driesch N, Mussler G, Stoica T, Mantl S, Ikonic Z, Luysberg M, Chiussi S, Hartmann J M, Sigg H, Faist J, Buca D, Grützmacher D 2015 Nat. Photonics 9 88 Google Scholar
[11]	Arakawa Y, Nakamura T, Urino Y, Fujita T 2013 IEEE Commun. Mag. 51 72 Google Scholar
[12]	Wu S T, Zhang L, Wan R Q, Zhou H, Lee K H, Chen Q M, Huang Y C, Gong X, Tan C S 2023 Photonics Res. 11 1606 Google Scholar
[13]	Liu X Q, Zhang J, Niu C Q, Liu T R, Huang Q X, Li M M, Zhang D D, Pang Y Q, Liu Z, Zuo Y H, Cheng B W 2022 Photonics Res. 10 1567 Google Scholar
[14]	Ghosh S, Sun G, Yu S Q, Chang G E 2025 IEEE J. Sel. Top. Quantum Electron. 31 1 Google Scholar
[15]	黄诗浩, 谢文明, 汪涵聪, 林光杨, 王佳琪, 黄巍, 李成 2018 67 040501 Google Scholar Huang S H, Xie W M, Wang H C, Lin G Y, Wang J Q, Huang W, Li C 2018 Acta Phys. Sin. 67 040501 Google Scholar
[16]	Huang S H, Zheng Q Q, Xie W M, Lin J Y, Huang W, Li C, Qi D F 2018 J. Phys. Condens. Matter 30 465701 Google Scholar
[17]	Murphy-Armando F, Murray É D, Savić I, Trigo M, Reis D A, Fahy S 2023 Appl. Phys. Lett. 122 012202 Google Scholar
[18]	Wang C, Wang H, Chen W, Xie X, Zong J, Liu L, Jin S, Zhang Y, Yu F, Meng Q, Tian Q, Wang L, Ren W, Li F, Zhang H, Zhang Y 2021 Nano Lett. 21 8258 Google Scholar
[19]	Stern M J, René de Cotret L P, Otto M R, Chatelain R P, Boisvert J P, Sutton M, Siwick B J 2018 Phys. Rev. B 97 165416 Google Scholar
[20]	Huang P, Zhang Y, Hu K, Qi J, Zhang D, Cheng L 2024 Chin. Phys. B 33 017201 Google Scholar
[21]	Rogowicz E, Kopaczek J, Kutrowska-Girzycka J, Myronov M, Kudrawiec R, Syperek M 2021 ACS Appl. Electron. Mater. 3 344 Google Scholar
[22]	Rideau D, Feraille M, Ciampolini L, Minondo M, Tavernier C, Jaouen H, Ghetti A 2006 Phys. Rev. B 74 195208 Google Scholar
[23]	Song Z, Fan W, Tan C S, Wang Q, Nam D, Zhang D H, Sun G 2019 New J. Phys. 21 073037 Google Scholar
[24]	Lever L, Ikonić Z, Valavanis A, Kelsall R W, Myronov M, Leadley D R, Hu Y, Owens N, Gardes F Y, Reed G T 2012 J. Appl. Phys. 112 123105 Google Scholar
[25]	Liu S Q, Yen S T 2019 J. Appl. Phys. 125 245701 Google Scholar
[26]	Wang X, Li H, Camacho-Aguilera R, Cai Y, Kimerling L C, Michel J, Liu J 2013 Opt. Lett. 38 652 Google Scholar
[27]	Claussen S A, Tasyurek E, Roth J E, Miller D A B 2010 Opt. Express 18 25596 Google Scholar
[28]	Zhou X Q, van Driel H M, Mak G 1994 Phys. Rev. B 50 5226 Google Scholar
[29]	Mak G, van Driel H M 1994 Phys. Rev. B 49 16817 Google Scholar

Cited By

图 1 Ge_1–x Sn_x材料的能带参数　(a) Γ能谷与L能谷的能量差值与Sn组分之间的关系; (b)导带电子状态密度与Sn组分之间的关系　　

Figure 1. Parameters of Ge_1–x Sn_x: (a) The energy difference of Γ and L valley as a function of composition x; (b) the electron density of states (DOS) effective masses at Γ and L valley as a function of composition x.

DownLoad: Full-Size Img PowerPoint

图 2 Ge_1–x Sn_x材料的谷间散射率　(a) Γ能谷到L能谷的散射率与能量的关系; (b) L能谷到Γ能谷的散射率与能量的关系

Figure 2. Inter-valley scattering rate (a) from Γ to L valleys and (b) from L to Γ valley with different Sn compositions.

DownLoad: Full-Size Img PowerPoint

图 3 谷间散射率与注入电子之间的关系　(a) Γ能谷到L能谷的谷间散射率; (b) L能谷到Γ能谷的散射率

Figure 3. Relationship between inter-valley scattering rate and inject electron density under the condition of different Sn compositions: (a) From Γ to L valleys scattering; (b) from L to Γ valley scattering.

DownLoad: Full-Size Img PowerPoint

图 4 谷间光学声子散射率与Sn组分之间的关系

Figure 4. Inter-valley scattering rate from Γ to L valleys scattering and from L to Γ valley scattering under different Sn compositions.

DownLoad: Full-Size Img PowerPoint

图 5 Ge_1–x Sn_x材料注入电子浓度与电子转移时间的关系(对数坐标), 插图为线性坐标

Figure 5. Relationship between electron transmission time and electron density in Γ, L valleys with various Sn compositions, the inset shows as a linear scale.

DownLoad: Full-Size Img PowerPoint

图 6 散射时间常数与Sn组分的关系

Figure 6. Relationship between composition and time-delay.

DownLoad: Full-Size Img PowerPoint

图 7 考虑与不考虑散射模型的情况下, Γ能谷、L能谷电子填充率与Sn组分的关系

Figure 7. Simulated electron population ratio for Γ and L valleys as a function of Sn compositions, with and without the scattering model.

DownLoad: Full-Size Img PowerPoint

map

[1]	Miao Y H, Wang G L, Kong Z Z, Xu B Q, Zhao X W, Luo X, Lin H X, Dong Y, Lu B, Dong L P, Zhou J R, Liu J B, Radamson H H 2021 Nanomaterials 11 2556 Google Scholar
[2]	Oka H, Mizubayashi W, Ishikawa Y, Uchida N, Mori T, Endo K 2021 Appl. Phys. Express 14 096501 Google Scholar
[3]	Zhang D, Song J J, Xue X X, Zhang S Q 2022 Chin. Phys. B 31 068401 Google Scholar
[4]	Wang H J, Han G Q, Jiang X W, Liu Y, Zhang J C, Hao Y 2019 IEEE Trans. Electron Devices 66 1985 Google Scholar
[5]	Wang P C, Huang P R, Ghosh S, Bansal R, Jheng Y T, Lee K C, Cheng H H, Chang G E 2024 ACS Photonics 11 2659 Google Scholar
[6]	Reboud V, Concepción O, Du W, El Kurdi M, Hartmann J M, Ikonic Z, Assali S, Pauc N, Calvo V, Cardoux C, Kroemer E, Coudurier N, Rodriguez P, Yu S Q, Buca D, Chelnokov A 2024 Photon. Nanostruc. Fundam. Appl. 58 101233 Google Scholar
[7]	Zheng J, Liu Z, Xue C L, Li C B, Zuo Y H, Cheng B W, Wang Q M 2018 J. Semicond. 39 061006 Google Scholar
[8]	Zhou Y Y, Dou W, Du W, Pham T, Ghetmiri S A, Al-Kabi S, Mosleh A, Alher M, Margetis J, Tolle J, Sun G, Soref R, Li B, Mortazavi M, Naseem H, Yu S Q 2016 J. Appl. Phys. 120 023102 Google Scholar
[9]	Ghetmiri S A, Du W, Margetis J, Mosleh A, Cousar L, Conley B R, Domulevicz L, Nazzal A, Sun G, Soref R A, Tolle J, Li B, Naseem H A, Yu S Q 2014 Appl. Phys. Lett. 105 151109 Google Scholar
[10]	Wirths S, Geiger R, von den Driesch N, Mussler G, Stoica T, Mantl S, Ikonic Z, Luysberg M, Chiussi S, Hartmann J M, Sigg H, Faist J, Buca D, Grützmacher D 2015 Nat. Photonics 9 88 Google Scholar
[11]	Arakawa Y, Nakamura T, Urino Y, Fujita T 2013 IEEE Commun. Mag. 51 72 Google Scholar
[12]	Wu S T, Zhang L, Wan R Q, Zhou H, Lee K H, Chen Q M, Huang Y C, Gong X, Tan C S 2023 Photonics Res. 11 1606 Google Scholar
[13]	Liu X Q, Zhang J, Niu C Q, Liu T R, Huang Q X, Li M M, Zhang D D, Pang Y Q, Liu Z, Zuo Y H, Cheng B W 2022 Photonics Res. 10 1567 Google Scholar
[14]	Ghosh S, Sun G, Yu S Q, Chang G E 2025 IEEE J. Sel. Top. Quantum Electron. 31 1 Google Scholar
[15]	黄诗浩, 谢文明, 汪涵聪, 林光杨, 王佳琪, 黄巍, 李成 2018 67 040501 Google Scholar Huang S H, Xie W M, Wang H C, Lin G Y, Wang J Q, Huang W, Li C 2018 Acta Phys. Sin. 67 040501 Google Scholar
[16]	Huang S H, Zheng Q Q, Xie W M, Lin J Y, Huang W, Li C, Qi D F 2018 J. Phys. Condens. Matter 30 465701 Google Scholar
[17]	Murphy-Armando F, Murray É D, Savić I, Trigo M, Reis D A, Fahy S 2023 Appl. Phys. Lett. 122 012202 Google Scholar
[18]	Wang C, Wang H, Chen W, Xie X, Zong J, Liu L, Jin S, Zhang Y, Yu F, Meng Q, Tian Q, Wang L, Ren W, Li F, Zhang H, Zhang Y 2021 Nano Lett. 21 8258 Google Scholar
[19]	Stern M J, René de Cotret L P, Otto M R, Chatelain R P, Boisvert J P, Sutton M, Siwick B J 2018 Phys. Rev. B 97 165416 Google Scholar
[20]	Huang P, Zhang Y, Hu K, Qi J, Zhang D, Cheng L 2024 Chin. Phys. B 33 017201 Google Scholar
[21]	Rogowicz E, Kopaczek J, Kutrowska-Girzycka J, Myronov M, Kudrawiec R, Syperek M 2021 ACS Appl. Electron. Mater. 3 344 Google Scholar
[22]	Rideau D, Feraille M, Ciampolini L, Minondo M, Tavernier C, Jaouen H, Ghetti A 2006 Phys. Rev. B 74 195208 Google Scholar
[23]	Song Z, Fan W, Tan C S, Wang Q, Nam D, Zhang D H, Sun G 2019 New J. Phys. 21 073037 Google Scholar
[24]	Lever L, Ikonić Z, Valavanis A, Kelsall R W, Myronov M, Leadley D R, Hu Y, Owens N, Gardes F Y, Reed G T 2012 J. Appl. Phys. 112 123105 Google Scholar
[25]	Liu S Q, Yen S T 2019 J. Appl. Phys. 125 245701 Google Scholar
[26]	Wang X, Li H, Camacho-Aguilera R, Cai Y, Kimerling L C, Michel J, Liu J 2013 Opt. Lett. 38 652 Google Scholar
[27]	Claussen S A, Tasyurek E, Roth J E, Miller D A B 2010 Opt. Express 18 25596 Google Scholar
[28]	Zhou X Q, van Driel H M, Mak G 1994 Phys. Rev. B 50 5226 Google Scholar
[29]	Mak G, van Driel H M 1994 Phys. Rev. B 49 16817 Google Scholar

[1]	Liu Wei, Ping Yun-Xia, Yang Jun, Xue Zhong-Ying, Wei Xing, Wu Ai-Min, Yu Wen-Jie, Zhang Bo. Reaction of titanium-modulated nickel with germanium-tin under microwave and rapid thermal annealing. Acta Physica Sinica, 2021, 70(11): 116801. doi: 10.7498/aps.70.20202118
[2]	Wu Hong, Li Feng. Mechanisms on the GeH/ interactions in germanene/germanane bilayer for tuning band structures. Acta Physica Sinica, 2016, 65(9): 096801. doi: 10.7498/aps.65.096801
[3]	Wu Hai-Na, Sun Xue, Gong Wei-Jiang, Yi Guang-Yu. Influences of electron-phonon interaction on the thermoelectric effect in a parallel double quantum dot system. Acta Physica Sinica, 2015, 64(7): 077301. doi: 10.7498/aps.64.077301
[4]	Su Shao-Jian, Zhang Dong-Liang, Zhang Guang-Ze, Xue Chun-Lai, Cheng Bu-Wen, Wang Qi-Ming. High-quality Ge1-xSnx alloys grown on Ge(001) substrates by molecular beam epitaxy. Acta Physica Sinica, 2013, 62(5): 058101. doi: 10.7498/aps.62.058101
[5]	Luo Zhi-Hua, Liang Guo-Dong. Non-classical eigen state and the persistent current in one-dimensional mesoscopic ring with the electron-two-phonon interaction. Acta Physica Sinica, 2012, 61(5): 057303. doi: 10.7498/aps.61.057303
[6]	Liang Guo-Dong, Luo Zhi-Hua. Non-classical state effect on the persistent current in one-dimensional mesoscopic ring with electron-phonon interaction. Acta Physica Sinica, 2011, 60(3): 037303. doi: 10.7498/aps.60.037303
[7]	Wang Xiao-Yan, Zhang He-Ming, Song Jian-Jun, Ma Jian-Li, Wang Guan-Yu, An Jiu-Hua. Electron mobility of strained Si/(001)Si1- x Ge x. Acta Physica Sinica, 2011, 60(7): 077205. doi: 10.7498/aps.60.077205
[8]	Zhao Feng-Qi, Zhou Bing-Qing. Energy levels of a polaron in wurtzite nitride parabolic quantum well under external electric field. Acta Physica Sinica, 2007, 56(8): 4856-4863. doi: 10.7498/aps.56.4856
[9]	Xia Zhi-Lin, Fan Zheng-Xiu, Shao Jian-Da. Electrons-phonons collision velocity in films radiated by laser. Acta Physica Sinica, 2006, 55(6): 3007-3012. doi: 10.7498/aps.55.3007
[10]	Zhang Hong-Qun, Liu Shao-Jun, Li Rong-Wu. The study on the Peierls phase transition of TTF-TCNQ. Acta Physica Sinica, 2005, 54(7): 3317-3320. doi: 10.7498/aps.54.3317
[11]	Zhang Hong-Qun. The study on the Peierls phase transition of one-dimensional organic conductors. Acta Physica Sinica, 2004, 53(4): 1162-1165. doi: 10.7498/aps.53.1162
[12]	CHEN DAN-PING, JIANG XIONG-WEI, ZHU CONG-SHAN. STUDY ON THE THERMOCHROMIC PROPERTIES OF Bi2O3-Li2O GLASSES. Acta Physica Sinica, 2001, 50(8): 1501-1506. doi: 10.7498/aps.50.1501
[13]	LI MI. THE INTERATOMIC INTERACTION AND PHONON DISPERSIONS IN IRON. Acta Physica Sinica, 2000, 49(9): 1692-1695. doi: 10.7498/aps.49.1692
[14]	Jin Kui-Juan, Pan Shao-Hua, Yang Guo-Zheng. . Acta Physica Sinica, 1995, 44(2): 299-304. doi: 10.7498/aps.44.299
[15]	YU CHAO-FAN, CHEN BIN, HE GUO-ZHU. INFLUENCE OF INTERACTION BETWEEN ELECTRONS AND PHONONS ON THE MAGNETIC EXCITATION OF ITINERANT ELECTRONS SYSTEM. Acta Physica Sinica, 1994, 43(5): 839-845. doi: 10.7498/aps.43.839
[16]	YANG GUANG-CAN. THE NONLINEAR THEORY OF INTERACTION BETWEEN LIGHT AND MATTER DESCRIBED BY q-DEFOR- MED OSCILLATOR MODEL. Acta Physica Sinica, 1994, 43(4): 521-529. doi: 10.7498/aps.43.521
[17]	FU RONG-TANG, LI LIE-MING, SUN XIN, FU ROU-LI. ELECTRON-PHONON INTERACTION AND NONLINEAR OPTICAL SUSCEPTIBILITY OF POLYMER. Acta Physica Sinica, 1993, 42(3): 422-430. doi: 10.7498/aps.42.422
[18]	LIU FU-SUI, FAN XI-QING, LIU YAN-ZHANC, WANG HUAI-SHENG, RUAN YING-CHAO. EFFECT OF ELECTRON-MANY PHONON INTERACTION ON SCATTERING TIME. Acta Physica Sinica, 1989, 38(1): 154-158. doi: 10.7498/aps.38.154
[19]	SHEN WEN-DA, ZHU SHI-TONG. EFFECTS OF COULOMB INTERACTION ON THE STIMULATED SCATTERING BY RELATIVISTIC ELECTRON BEAMS. Acta Physica Sinica, 1982, 31(2): 234-236. doi: 10.7498/aps.31.234
[20]	CHENG C. S., CHANG W. Y., LIU C. H., LIU C. C.. A PHASE DIAGRAM OF THE ALLOYS OF THE TERNARY SYSTEM OF COPPER-GERMANIUM-TIN. Acta Physica Sinica, 1966, 22(4): 423-428. doi: 10.7498/aps.22.423

Catalog

Vol. 74, Issue 3 - 2025-02-05

Metrics

Abstract views: 633
PDF Downloads: 23
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板