Rapid-transfer matrix method for analyzing electromagnetic properties of uniaxial/biaxial bianisotropic media

Fan Jiu-Yang; Zhang Yu-Xian; Feng Xiao-Li; Huang Zhi-Xiang

doi:10.7498/aps.73.20241346

Abstract

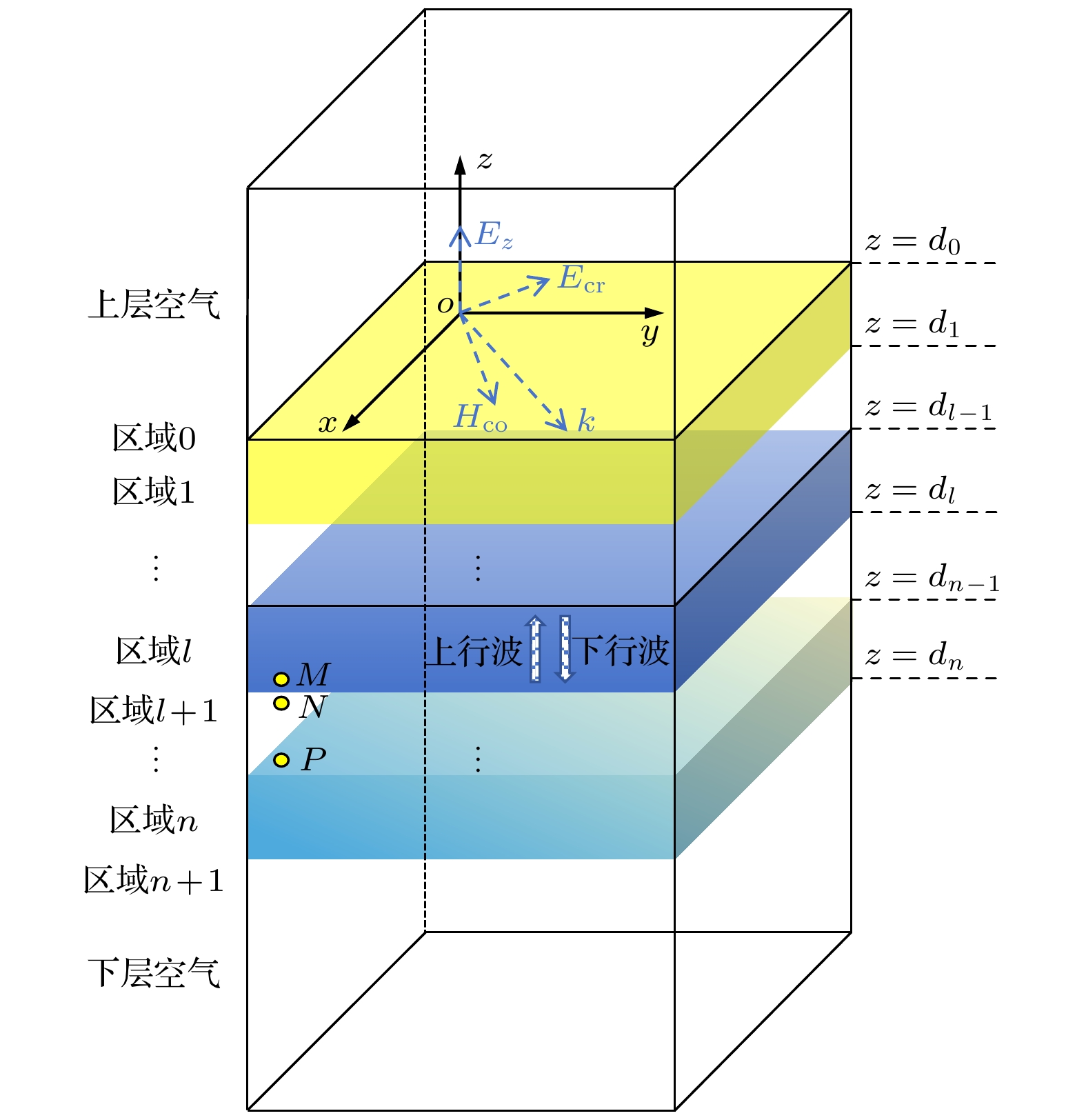
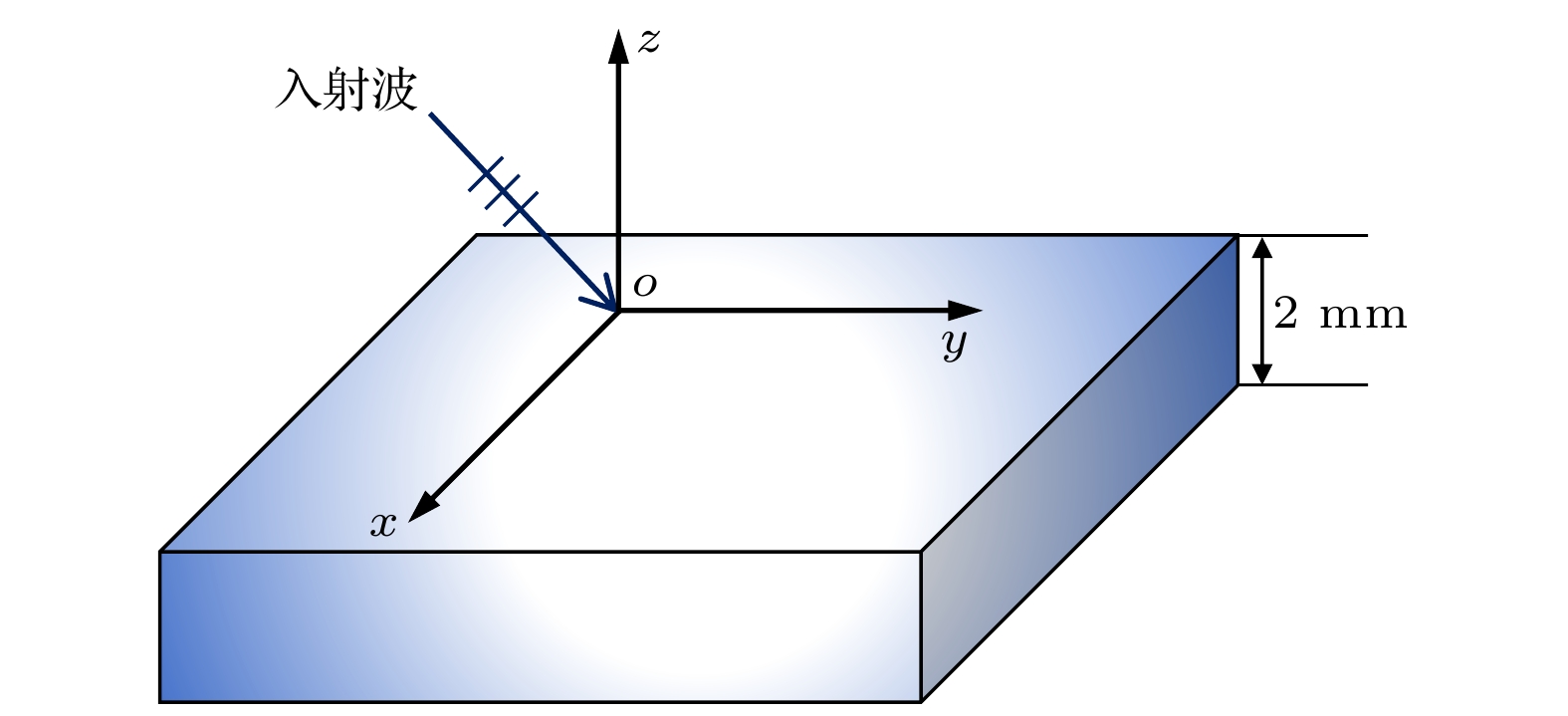
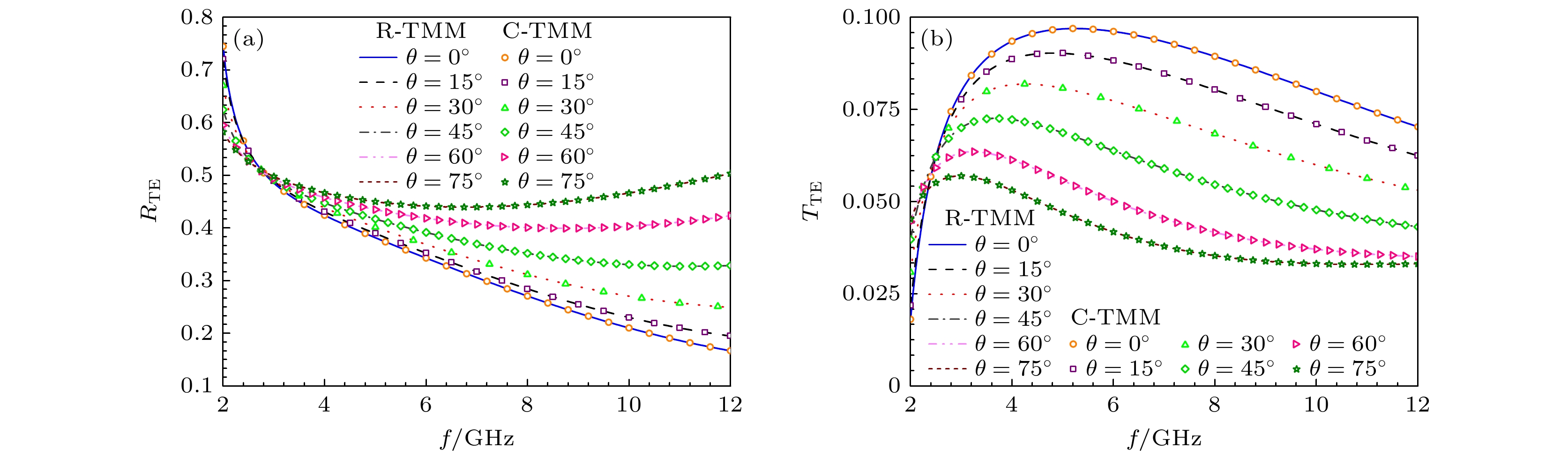
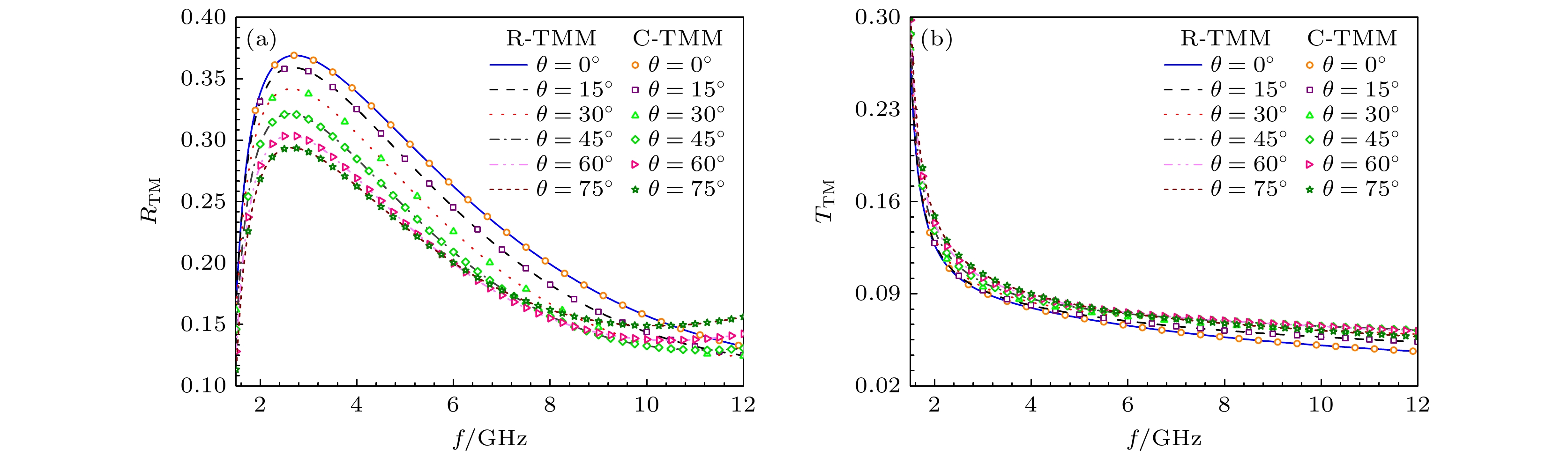
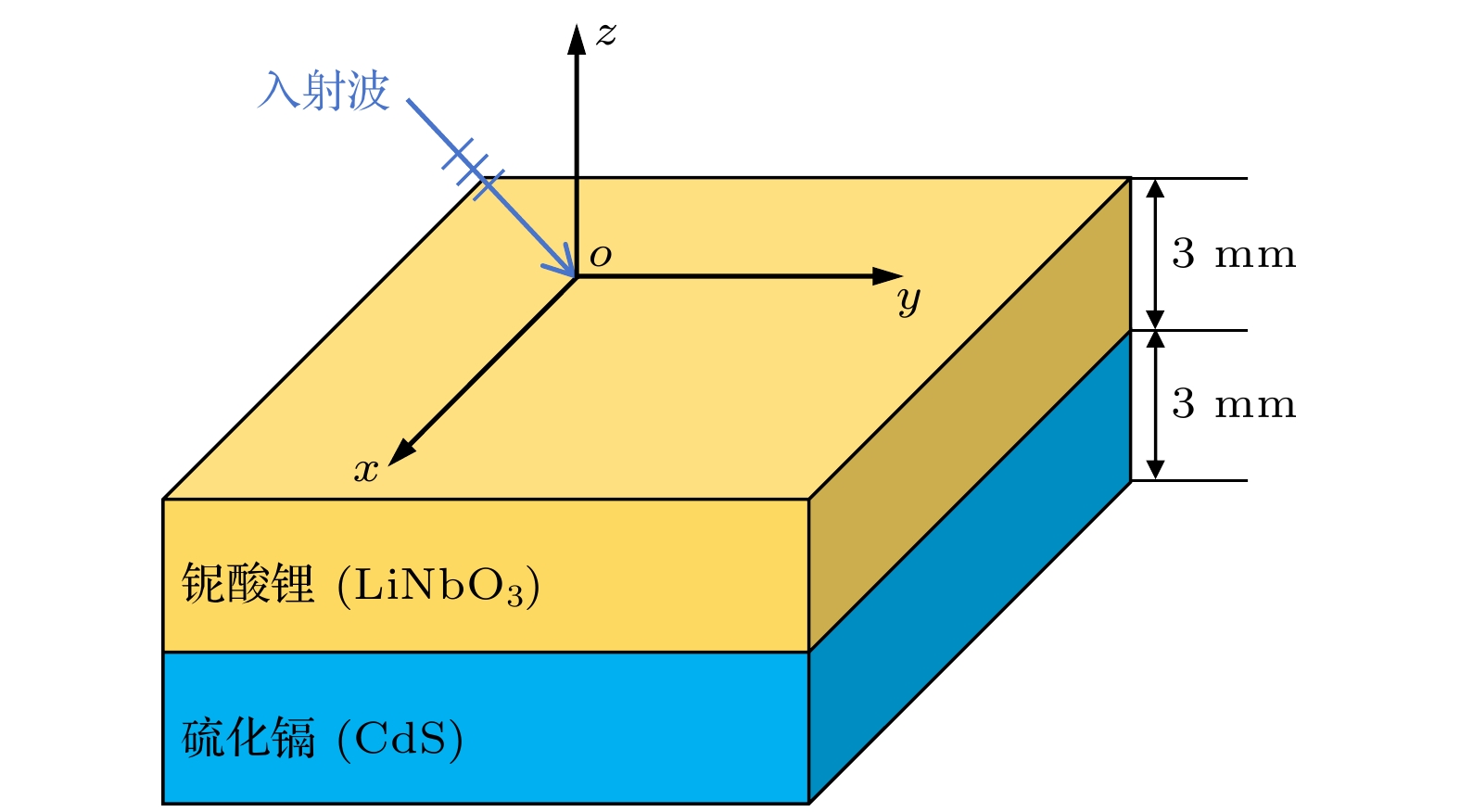
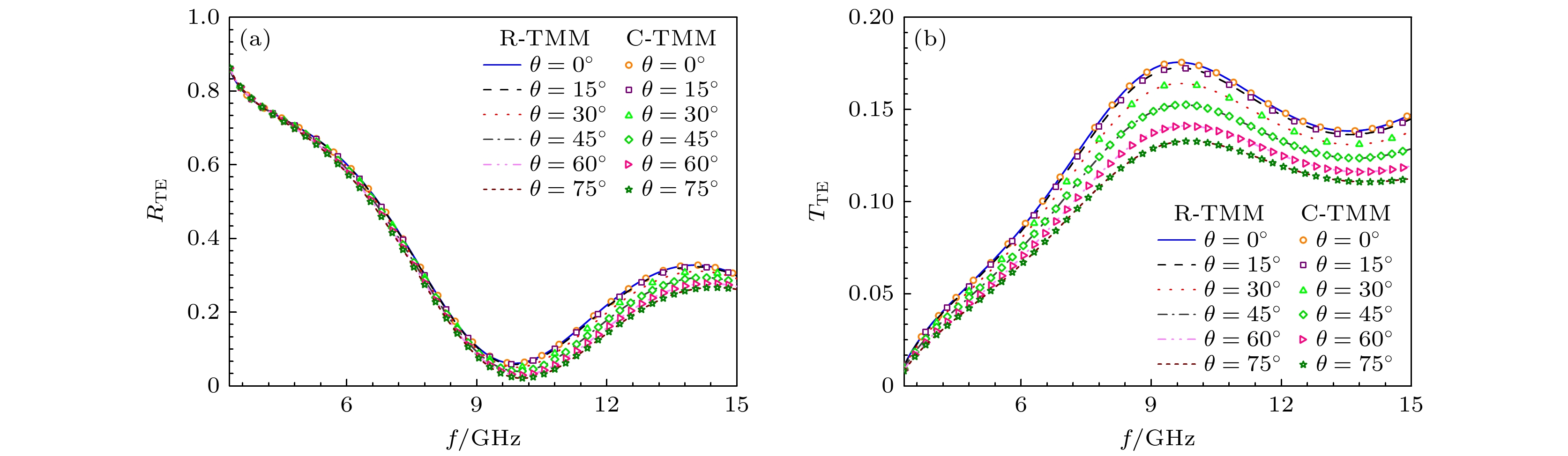
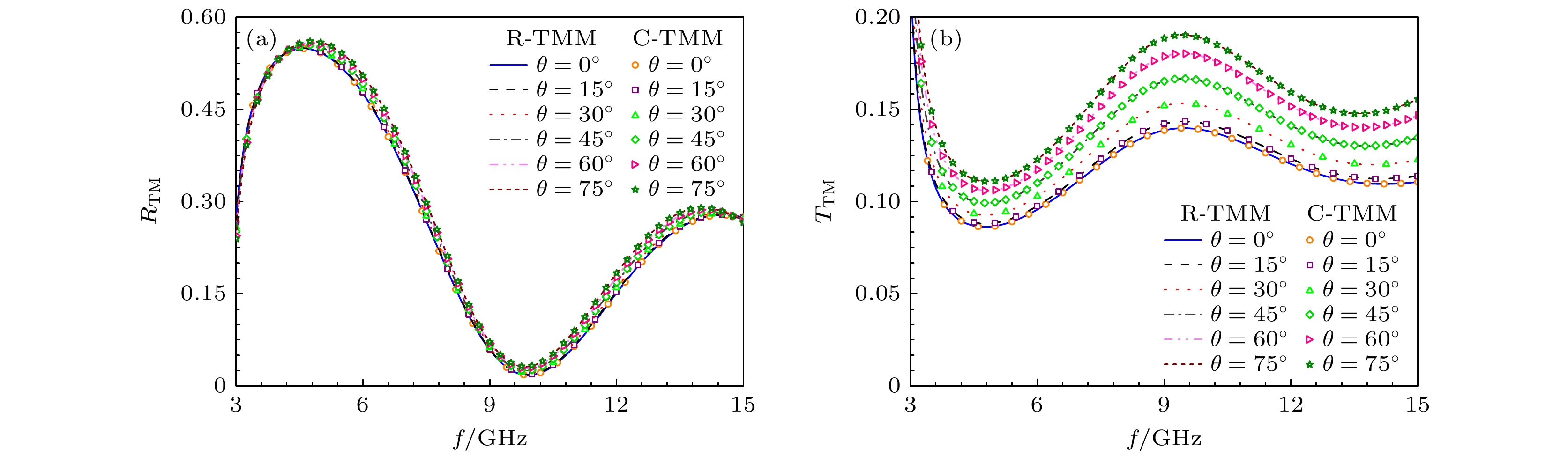
Uniaxial/biaxial bianisotropic materials are widespreadly used in manufacturing optical devices , owing to their distinctive electromagnetic response characteristics. To effectively analyze the electromagnetic properties of uniaxial/biaxial bianisotropic materials, rapid-transfer matrix method (R-TMM) to investigate the propagation process of plane waves in the media is proposed. Starting from the Maxwell’s equations in the time domain, a homogeneous differential equation about the electric field is constructed by processing the matrix containing dielectric and magnetic conductivity, electric and magnetic loss, tellegen and chirality carrier parameters, and the complex matrix operation is applied to that equation to obtain the Booker quartic equation, and then the formulae method is utilized to obtain the eigenvalues in the uniaxial/biaxial bianisotropic media. Subsequently, the tangential continuity of layered media at the interface is employed to establish a transfer matrix for single-layered media. In the case of multi-layered media, the transfer matrix of plane waves propagating in multi-layered uniaxial/biaxial bianisotropic media can be obtained by means of a continuous iteration process based on the transfer matrix of single-layered media. The formula for calculating the propagation coefficients of uniaxial/biaxial bianisotropic materials can be derived based on the different upward and downward waves in the reflection/transmission region. Finally, the reliability and efficiency of R-TMM are verified from two numerical experiments with the plane waves incident at different angles on uniaxial/biaxial bianisotropic media. The first experiment is designed as a single-layered biaxial bianisotropic model with more general electromagnetic parameters, and the second experiment is designed as a double-layered uniaxial and biaxial bianisotropic model consisting of common optical materials, which are composed of two non-magnetic materials, lithium niobate (LiNbO₃) and cadmium sulfide (CdS). The experimental results demonstrate that compared with the conventional conventional-transfer matrix method (C-TMM), the R-TMM reduces the computational memory and CPU time required for calculating the reflection and transmission coefficients of the uniaxial/biaxial bianisotropic model by over 98%, while maintaining the accuracy of the reflection and transmission coefficient calculations. Therefore, R-TMM provides an efficient and dependable approach for the designing complex optical devices and analyzing uniaxial/biaxial bianisotropic propagation characteristics.

Keywords:

Authors and contacts

1.
School of Electronic and Engineering, Anhui University, Hefei 230601, China
2.
Information Materials and Intelligent Sensing Laboratory of Anhui Province, Anhui University, Hefei 230601, China
3.
Industry-Education-Research Institute of Advanced Materials and Technology for Integrated Circuits, Anhui University, Hefei 230601, China

Corresponding author: Zhang Yu-Xian, yxzhang_tute@126.com

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 62101333) and the Program for Excellent Scientific and Innovation Research Team of Anhui Province, China (Grant No. 2022AH010002).

FullText HTML

References

[1]	Chen Y X, Duan G Y, Xu C Y, Qin X F, Zhao Q, Zhou H Q, Wang B X 2024 Diam. Relat. Mater. 143 110939 Google Scholar
[2]	Hosseini K, Atlasbaf Z 2018 IEEE Trans. Antennas Propag. 66 7483 Google Scholar
[3]	Ahmed F, Hassan T, Shoaib N 2020 IEEE Antennas Wirel. Propag. Lett. 19 1833 Google Scholar
[4]	Dong Z J, Feng X, Zhou H Q, Liu C, Zhang M H, Liang W J 2023 IEEE Trans. Geosci. Remote Sens. 61 4503120 Google Scholar
[5]	Kong J A 1972 Proc. IEEE 60 1036 Google Scholar
[6]	王一平 2007 工程电动力学 (第二版) (西安: 西安电子科技大学出版社) 第23−24页 Wang Y P 2007 Engineering Electrodynamics (2rd Ed.) (Xi’ an: Xidian University Press) pp23–24
[7]	Zarifi D, Soleimani M, Abdolali A 2014 IEEE Trans. Antennas Propag. 62 1538 Google Scholar
[8]	Dimitriadis A I, Kantartzis N V, Tsiboukis T D 2013 IEEE Trans. Magn. 49 1769 Google Scholar
[9]	Mousvai S M, Arand B A, Forooraghi K 2021 IEEE Access. 9 54241 Google Scholar
[10]	Hasar U C, Ozturk G, Kaya Y, Barroso J J, Ertugrul M 2021 IEEE Trans. Antennas Propag. 69 7064 Google Scholar
[11]	Karimi P, Rejaei B, Khavasi A 2023 IEEE Trans. Antennas Propag. 71 2507 Google Scholar
[12]	陈伟, 黄海, 杨利霞, 薄勇, 黄志祥 2023 72 060201 Google Scholar Chen W, Huang H, Yang L X, Bo Y, Huang Z X 2023 Acta Phys. Sin. 72 060201 Google Scholar
[13]	谢国大, 侯桂林, 牛凯坤, 冯乃星, 方明, 李迎松, 黄志祥 2023 72 150201 Google Scholar Xie G D, Hou G L, Niu K K, Feng N X, Fang M, Li Y S, Huang Z X 2023 Acta Phys. Sin. 72 150201 Google Scholar
[14]	Demarest K 1987 IEEE Trans. Antennas Propag. 35 826 Google Scholar
[15]	葛德彪, 闫玉波 2005 电磁波时域有限差分方法 (第三版) (西安: 西安电子科技大学出版社) 第259—294页 Ge D B, Yan Y B 2005 Finite-Difference Time-Domain Method for Electromagnetic Waves (3rd Ed.) (Xi’an: Xidian University Press) pp259−294
[16]	王飞, 葛德彪, 魏兵 2009 58 6356 Google Scholar Wang F, Ge D B, Wei B 2009 Acta Phys. Sin. 58 6356 Google Scholar
[17]	Greenwood A D, Jin J M 1999 IEEE Trans. Antennas Propag. 47 1260 Google Scholar
[18]	孙宏祥, 许伯强, 王纪俊, 徐桂东, 徐晨光, 王峰 2009 58 6344 Google Scholar Sun H X, Xu B Q, Wang J J, Xu G D, Xu C G, Wang F 2009 Acta Phys. Sin. 58 6344 Google Scholar
[19]	Hanninen I, Nikoskinen K 2008 IEEE Trans. Antennas Propag. 56 278 Google Scholar
[20]	王哲, 王秉中 2014 63 120202 Google Scholar Wang Z, Wang B Z 2014 Acta Phys. Sin. 63 120202 Google Scholar
[21]	葛德彪, 魏兵 2011 电磁波理论 (北京: 科学出版社) 第62—73页 Ge D B, Wei B 2011 Electromagnetic Waves Theory (Beijing: Science Press) pp62−73
[22]	Johnston T W 1969 Radio Sci. 4 729 Google Scholar
[23]	Chen H C 1981 Radio Sci. 16 1213 Google Scholar
[24]	Tan E L, Tan S Y 1999 IEEE Trans. Antennas Propag. 47 1820 Google Scholar
[25]	郑宏兴, 葛德彪 2000 49 1702 Google Scholar Zheng H X, Ge D B 2000 Acta Phys. Sin. 49 1702 Google Scholar
[26]	Jiang Y Y, Shi H Y, Zhang Y Q, Hou C F, Sun X D 2007 Chin. Phys. 16 1959 Google Scholar
[27]	Sarrafi P, Qian L 2012 IEEE J. Quantum Electron. 48 559 Google Scholar
[28]	王飞, 魏兵 2019 68 244101 Google Scholar Wang F, Wei B 2019 Acta Phys. Sin. 68 244101 Google Scholar
[29]	Zhang Y X, Feng N X, Wang G P, Zheng H X 2021 IEEE Trans. Antennas Propag. 69 4727 Google Scholar

Cited By

图 1 平面波在单轴/双轴双各向异性媒质中的双折射现象

Figure 1. Birefringence phenomenon of plane waves in uniaxial/biaxial bianisotropic media.

DownLoad: Full-Size Img PowerPoint

图 2 平面波在层状单轴/双轴双各向异性媒质中传播

Figure 2. Propagation of plane waves in layered uniaxial/biaxial bianisotropic media.

DownLoad: Full-Size Img PowerPoint

图 3 单层媒质的模型图

Figure 3. Model diagram of single-layered medium.

DownLoad: Full-Size Img PowerPoint

图 4 TE模式下, 单层双轴双各向异性媒质传播系数的对比　(a)反射系数; (b)透射系数

Figure 4. Comparison of propagation coefficients for single-layered biaxial bianisotropic media in TE mode: (a) Reflection coefficient; (b) transmission coefficient.

DownLoad: Full-Size Img PowerPoint

图 5 TM模式下, 单层双轴双各向异性媒质传播系数的对比　(a)反射系数; (b)透射系数

Figure 5. Comparison of propagation coefficients for single-layered biaxial bianisotropic media in TM mode: (a) Reflection coefficient; (b) transmission coefficient.

DownLoad: Full-Size Img PowerPoint

图 6 多层光学材料模型图

Figure 6. Model diagram of multi-layered optical material.

DownLoad: Full-Size Img PowerPoint

图 7 TE模式下, 多层光学材料传播系数的对比　(a)反射系数; (b)透射系数

Figure 7. Comparison of propagation coefficients for multi-layered optical materials in TE mode: (a) Reflection coefficients; (b) transmission coefficients.

DownLoad: Full-Size Img PowerPoint

图 8 TM模式下, 多层光学材料传播系数的对比　(a)反射系数; (b)透射系数

Figure 8. Comparison of propagation coefficients for multi-layered optical materials in TM mode: (a) Reflection coefficients; (b) transmission coefficients.

DownLoad: Full-Size Img PowerPoint

表 1 单层双轴双各向异性的电磁参数

Table 1. Electromagnetic parameters of single-layered biaxial bianisotropic medium.

$\boldsymbol\varepsilon_{\rm r}$	$\boldsymbol \mu_{\rm r} $	$\boldsymbol \sigma_{\rm e} $	$\boldsymbol \sigma_{\rm m} $
$ \left[ {\begin{array}{*{20}{c}} {5.6}&0&0 \\ 0&{4.8}&0 \\ 0&0&{6.1} \end{array}} \right] $	$ \left[ {\begin{array}{*{20}{c}} {2.9}&0&0 \\ 0&{4.2}&0 \\ 0&0&{2.6} \end{array}} \right] $	$ \left[ {\begin{array}{*{20}{c}} {2.9}&0&0 \\ 0&{4.2}&0 \\ 0&0&{2.6} \end{array}} \right] $	$ \left[ {\begin{array}{*{20}{c}} {271}&0&0 \\ 0&{422}&0 \\ 0&0&{354} \end{array}} \right] $

$\boldsymbol \xi $		$\boldsymbol \zeta $
$ \left[ {\begin{array}{*{20}{c}} {3.9 + 0.01{\text{j}}}&0&0 \\ 0&{5.3 + 0.03{\text{j}}}&0 \\ 0&0&{4.3 + 0.06{\text{j}}} \end{array}} \right] $		$ \left[ {\begin{array}{*{20}{c}} {3.9 - 0.01{\text{j}}}&0&0 \\ 0&{5.3 - 0.03{\text{j}}}&0 \\ 0&0&{4.3 - 0.06{\text{j}}} \end{array}} \right] $

DownLoad: CSV

表 2 C-TMM和R-TMM计算单层媒质传播系数的效率比较

Table 2. Comparison of efficiency between C-TMM and R-TMM in calculating the propagation coefficients of single-layered medium.

方法	CPU核数	内存/MB	CPU时间/s
方法	CPU核数	内存/MB	TE	TM
C-TMM	1	729.4	9.2541	10.6075
R-TMM	1	5.3	0.1303	0.1521
比率 (R-TMM / C-TMM)		0.0073	0.01408	0.01434

DownLoad: CSV

表 3 两种光学材料的电磁参数

Table 3. Electromagnetic parameters of two optical materials.

Media	$\boldsymbol\varepsilon_{\rm r}$	$\boldsymbol\mu_{\rm r}$	$\boldsymbol\sigma_{\rm r}$	$\boldsymbol\sigma_{\rm r}$
LiNbO₃	$ \left[ {\begin{array}{*{20}{c}} {32.3}&0&0 \\ 0&{32.3}&0 \\ 0&0&{37.4} \end{array}} \right] $	$ \left[ {\begin{array}{*{20}{c}} {1.0}&0&0 \\ 0&{1.0}&0 \\ 0&0&{1.1} \end{array}} \right] $	$ \left[ {\begin{array}{*{20}{c}} {4.9}&0&0 \\ 0&{4.9}&0 \\ 0&0&{5.8} \end{array}} \right] $	$ \left[ {\begin{array}{*{20}{c}} {356}&0&0 \\ 0&{356}&0 \\ 0&0&{564} \end{array}} \right] $
CdS	$ \left[ {\begin{array}{*{20}{c}} {6.25}&0&0 \\ 0&{6.01}&0 \\ 0&0&{6.32} \end{array}} \right] $	$ \left[ {\begin{array}{*{20}{c}} {1.0}&0&0 \\ 0&{1.0}&0 \\ 0&0&{1.0} \end{array}} \right] $	$ \left[ {\begin{array}{*{20}{c}} {0.02}&0&0 \\ 0&{0.03}&0 \\ 0&0&{0.01} \end{array}} \right] $	$ \left[ {\begin{array}{*{20}{c}} 0&0&0 \\ 0&0&0 \\ 0&0&0 \end{array}} \right] $

Media	$\boldsymbol\xi $		$\boldsymbol\zeta $
LiNbO₃	$ \left[ {\begin{array}{*{20}{c}} {0.02}&0&0 \\ 0&{0.02}&0 \\ 0&0&{0.01} \end{array}} \right] $		$ \left[ {\begin{array}{*{20}{c}} {0.02}&0&0 \\ 0&{0.02}&0 \\ 0&0&{0.01} \end{array}} \right] $
CdS	$ \left[ {\begin{array}{*{20}{c}} {4.5 + 0.01{\text{j}}}&0&0 \\ 0&{6.6 + 0.02{\text{j}}}&0 \\ 0&0&{3.9 + 0.01{\text{j}}} \end{array}} \right] $		$ \left[ {\begin{array}{*{20}{c}} {4.5 - 0.01{\text{j}}}&0&0 \\ 0&{6.6 - 0.02{\text{j}}}&0 \\ 0&0&{3.9 - 0.01{\text{j}}} \end{array}} \right] $

DownLoad: CSV

表 4 C-TMM和R-TMM在计算多层光学材料传播系数时的效率对比

Table 4. Comparison of efficiency between C-TMM and R-TMM in calculating the propagation coefficient of multilayer optical materials.

方法	CPU核数	内存/MB	CPU时间/s
方法	CPU核数	内存/MB	TE	TM
C-TMM	1	744.2	11.8062	11.8935
R-TMM	1	7.6	0.1796	0.1851
比率 (R-TMM/C-TMM)		0.0102	0.0152	0.0156

DownLoad: CSV

map

[1]	Chen Y X, Duan G Y, Xu C Y, Qin X F, Zhao Q, Zhou H Q, Wang B X 2024 Diam. Relat. Mater. 143 110939 Google Scholar
[2]	Hosseini K, Atlasbaf Z 2018 IEEE Trans. Antennas Propag. 66 7483 Google Scholar
[3]	Ahmed F, Hassan T, Shoaib N 2020 IEEE Antennas Wirel. Propag. Lett. 19 1833 Google Scholar
[4]	Dong Z J, Feng X, Zhou H Q, Liu C, Zhang M H, Liang W J 2023 IEEE Trans. Geosci. Remote Sens. 61 4503120 Google Scholar
[5]	Kong J A 1972 Proc. IEEE 60 1036 Google Scholar
[6]	王一平 2007 工程电动力学 (第二版) (西安: 西安电子科技大学出版社) 第23−24页 Wang Y P 2007 Engineering Electrodynamics (2rd Ed.) (Xi’ an: Xidian University Press) pp23–24
[7]	Zarifi D, Soleimani M, Abdolali A 2014 IEEE Trans. Antennas Propag. 62 1538 Google Scholar
[8]	Dimitriadis A I, Kantartzis N V, Tsiboukis T D 2013 IEEE Trans. Magn. 49 1769 Google Scholar
[9]	Mousvai S M, Arand B A, Forooraghi K 2021 IEEE Access. 9 54241 Google Scholar
[10]	Hasar U C, Ozturk G, Kaya Y, Barroso J J, Ertugrul M 2021 IEEE Trans. Antennas Propag. 69 7064 Google Scholar
[11]	Karimi P, Rejaei B, Khavasi A 2023 IEEE Trans. Antennas Propag. 71 2507 Google Scholar
[12]	陈伟, 黄海, 杨利霞, 薄勇, 黄志祥 2023 72 060201 Google Scholar Chen W, Huang H, Yang L X, Bo Y, Huang Z X 2023 Acta Phys. Sin. 72 060201 Google Scholar
[13]	谢国大, 侯桂林, 牛凯坤, 冯乃星, 方明, 李迎松, 黄志祥 2023 72 150201 Google Scholar Xie G D, Hou G L, Niu K K, Feng N X, Fang M, Li Y S, Huang Z X 2023 Acta Phys. Sin. 72 150201 Google Scholar
[14]	Demarest K 1987 IEEE Trans. Antennas Propag. 35 826 Google Scholar
[15]	葛德彪, 闫玉波 2005 电磁波时域有限差分方法 (第三版) (西安: 西安电子科技大学出版社) 第259—294页 Ge D B, Yan Y B 2005 Finite-Difference Time-Domain Method for Electromagnetic Waves (3rd Ed.) (Xi’an: Xidian University Press) pp259−294
[16]	王飞, 葛德彪, 魏兵 2009 58 6356 Google Scholar Wang F, Ge D B, Wei B 2009 Acta Phys. Sin. 58 6356 Google Scholar
[17]	Greenwood A D, Jin J M 1999 IEEE Trans. Antennas Propag. 47 1260 Google Scholar
[18]	孙宏祥, 许伯强, 王纪俊, 徐桂东, 徐晨光, 王峰 2009 58 6344 Google Scholar Sun H X, Xu B Q, Wang J J, Xu G D, Xu C G, Wang F 2009 Acta Phys. Sin. 58 6344 Google Scholar
[19]	Hanninen I, Nikoskinen K 2008 IEEE Trans. Antennas Propag. 56 278 Google Scholar
[20]	王哲, 王秉中 2014 63 120202 Google Scholar Wang Z, Wang B Z 2014 Acta Phys. Sin. 63 120202 Google Scholar
[21]	葛德彪, 魏兵 2011 电磁波理论 (北京: 科学出版社) 第62—73页 Ge D B, Wei B 2011 Electromagnetic Waves Theory (Beijing: Science Press) pp62−73
[22]	Johnston T W 1969 Radio Sci. 4 729 Google Scholar
[23]	Chen H C 1981 Radio Sci. 16 1213 Google Scholar
[24]	Tan E L, Tan S Y 1999 IEEE Trans. Antennas Propag. 47 1820 Google Scholar
[25]	郑宏兴, 葛德彪 2000 49 1702 Google Scholar Zheng H X, Ge D B 2000 Acta Phys. Sin. 49 1702 Google Scholar
[26]	Jiang Y Y, Shi H Y, Zhang Y Q, Hou C F, Sun X D 2007 Chin. Phys. 16 1959 Google Scholar
[27]	Sarrafi P, Qian L 2012 IEEE J. Quantum Electron. 48 559 Google Scholar
[28]	王飞, 魏兵 2019 68 244101 Google Scholar Wang F, Wei B 2019 Acta Phys. Sin. 68 244101 Google Scholar
[29]	Zhang Y X, Feng N X, Wang G P, Zheng H X 2021 IEEE Trans. Antennas Propag. 69 4727 Google Scholar

[1]	Li Shun, Li Zheng-Jun, Qu Tan, Li Hai-Ying, Wu Zhen-Sen. Propagation of double zero-order Bessel beam and its scattering properties to uniaxial anisotropic spheres. Acta Physica Sinica, 2022, 71(18): 180301. doi: 10.7498/aps.71.20220491
[2]	Sun Juan, Li Xiao-Xia, Zhang Jin-Hao, Shen Yu-Zhuo, Li Yan-Yu. Synchronizability and eigenvalues of multilayer star networks through unidirectionally coupling. Acta Physica Sinica, 2017, 66(18): 188901. doi: 10.7498/aps.66.188901
[3]	Xu Ming-Ming, Lu Jun-An, Zhou Jin. Synchronizability and eigenvalues of two-layer star networks. Acta Physica Sinica, 2016, 65(2): 028902. doi: 10.7498/aps.65.028902
[4]	Jiao Bao-Bao. Eigenvalue problems solved by reorthogonalization Lanczos method for the large non-orthonormal sparse matrix. Acta Physica Sinica, 2016, 65(19): 192101. doi: 10.7498/aps.65.192101
[5]	Hao Ben-Jian, Li Zan, Wan Peng-Wu, Si Jiang-Bo. Passive source localization using RROA based on eigenvalue decomposition algorithm in WSNs. Acta Physica Sinica, 2014, 63(5): 054304. doi: 10.7498/aps.63.054304
[6]	He Sheng-Zhong, Zhou Guo-Hua, Xu Jian-Ping, Wu Song-Rong, Yan Tie-Sheng, Zhang Xi. Precise modeling and dynamic characteristics of valley V2 controlled Boost converter. Acta Physica Sinica, 2014, 63(17): 170503. doi: 10.7498/aps.63.170503
[7]	Dong Jian-Feng, Li Jie. Reflection and transmission characteristics of electromagnetic waves by the uniaxially anisotropic chiral slab. Acta Physica Sinica, 2013, 62(6): 064102. doi: 10.7498/aps.62.064102
[8]	Liang Yi, Wang Xing-Yuan. Pinning chaotic synchronization in complex networks on maximum eigenvalue of low order matrix. Acta Physica Sinica, 2012, 61(3): 038901. doi: 10.7498/aps.61.038901
[9]	Ji Ying, Bi Qin-Sheng. Bifurcation analysis of slow-fast behavior in modified Chua's circuit. Acta Physica Sinica, 2012, 61(1): 010202. doi: 10.7498/aps.61.010202
[10]	Zhu Ting-Xiang, Wu Ye, Xiao Jing-Hua. An efficient adaptive method of improving the synchronization of complex networks. Acta Physica Sinica, 2012, 61(4): 040502. doi: 10.7498/aps.61.040502
[11]	Hou Xiao-Juan, Yun Guo-Hong, Bai Yu-Hao, Bai Narsu, Zhou Wen-Ping. The eigenvalues of quantized spin waves and theeffect of the uniaxial anisotropy. Acta Physica Sinica, 2011, 60(5): 056805. doi: 10.7498/aps.60.056805
[12]	Li Zhuo-Xuan, Pei Li, Qi Chun-Hui, Peng Wan-Jing, Ning Ti-Gang, Zhao Rui-Feng, Gao Song. Fiber grating Fabry-Perot cavity studied by V-I transmission matrix method. Acta Physica Sinica, 2010, 59(12): 8615-8624. doi: 10.7498/aps.59.8615
[13]	Cao Jing-Xiao, Hu Wei, Luo Hai-Lu, Yang Xiang-Bo. The vectorial properties of paraxial beams propagating in uniaxial left-handed materials. Acta Physica Sinica, 2007, 56(4): 2131-2138. doi: 10.7498/aps.56.2131
[14]	Jiang Yong-Yuan, Zhang Yong-Qiang, Shi Hong-Yan, Hou Chun-Feng, Sun Xiu-Dong. The Goos-H?nchen shift on the surface of uniaxially anisotropic left-handed materials. Acta Physica Sinica, 2007, 56(2): 798-804. doi: 10.7498/aps.56.798
[15]	Zhuang Fei, Shen Jian-Qi. Investigation of photon geometric phases inside a curved fiber made of biaxially anisotropic left-handed media. Acta Physica Sinica, 2005, 54(2): 955-960. doi: 10.7498/aps.54.955
[16]	WANG HUI, LI YONG-PING. AN EIGEN MATRIX METHOD FOR OBTAINING THE BAND STRUCTURE OF PHOTONIC CRYSTALS. Acta Physica Sinica, 2001, 50(11): 2172-2178. doi: 10.7498/aps.50.2172
[17]	ZHENG HONG-XING GE, DE-BIAO. ELECTROMAGNETIC WAVE REFLECTION AND TRANSMISSION OF ANISOTROPIC LAYERED MEDIA BY GENERALIZED PROPAGATION MATRIX METHOD. Acta Physica Sinica, 2000, 49(9): 1702-1705. doi: 10.7498/aps.49.1702
[18]	LAI JIAN-WEN, ZHOU SHI-PING, LI GUO-HUI, XU DE-MING. A METHOD FOR COMPUTING LYAPUNOV EXPONENTS SPECTRA WITHOUT REORTHOGONALIZATION. Acta Physica Sinica, 2000, 49(12): 2328-2332. doi: 10.7498/aps.49.2328
[19]	Wang Yong-Qiang, Li Zhen-Ya. . Acta Physica Sinica, 1995, 44(5): 811-817. doi: 10.7498/aps.44.811
[20]	SHEN WEN-ZHONG, LI ZHEN-YA. SPIN WAVES IN A MAGNETIC SUPERLATTICE WITH SINGLE-ION UNIAXIAL ANISOTROPY. Acta Physica Sinica, 1992, 41(8): 1374-1379. doi: 10.7498/aps.41.1374

Catalog

Vol. 73, Issue 24 - 2024-12-20

Metrics

Abstract views: 1002
PDF Downloads: 59
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板