-
Discrete chaotic system, as a pseudo-random signal source, plays a very important role in realizing secure communication. However, many low-dimensional chaotic systems are prone to chaos degradation. Therefore, many scholars have studied the construction of high-dimensional chaotic systems. However, many existing algorithms for constructing high-dimensional chaotic systems have relatively high time complexity and relatively complex structures. To solve this problem, this paper explores an n-dimensional discrete hyperchaotic system with a simple structure. Firstly, the n-dimensional discrete hyperchaotic system is constructed by using sine function and power function and simple operations. Then, it is theoretically analyzed based on Jacobian matrix method that the system can have the positive Lyapunov exponents. Next, the algorithm time complexity, sample entropy, correlation dimension and other indexes are compared with those of the existing methods. The experimental results show that our system has a simple structure, high complexity and good algorithm time complexity. Therewith, a six-dimensional chaotic system is chosen as an example, and the phase diagram, bifurcation diagram, Lyapunov expnonents, complexity and other characteristics of the system are analyzed. The results show that the proposed system has good chaotic characteristics. Moreover, to show the application of the proposed system, we apply it to audio encryption. According to this system, we combine it with the XOR operation and true random numbers to explore a novel method of one-cipher audio encryption. Through experimental simulation, compared with some existing audio encryption algorithms, this algorithm can satisfy various statistical tests and resist various common attacks. It is also validated that the proposed system can be effectively applied to the field of audio encryption.
[1] Herbadji D, Herbadji A, haddad I, Kahia H, Belmeguenai A, Derouiche N 2024 Integration 97 102192
Google Scholar
[2] Joshi A B, Gaffar A 2024 Soft Comput. 28 5523
Google Scholar
[3] Yu F, Yu Q L, Chen H F, Kong X X, Molbel A A M, Cai S, Du S C 2022 Fractal Fract. 6 370
Google Scholar
[4] Wu R, Gao S, Wang X Y, Liu S B, Li Q, Erkan U, Tang X L 2022 Chaos, Soliton Fractals 165 112770
Google Scholar
[5] Wu R, Gao S, Iu H H, Zhou S, Erkan U, Toktas A, Tang X 2024 IEEE Internet Things J. 11 10214
Google Scholar
[6] Rahul B, Kuppusamy K, Senthilrajan A 2023 Multimed. Tools Appl. 82 43729
Google Scholar
[7] Demirtaş M 2023 Orclever Proc. Res. Dev. 2 28
Google Scholar
[8] Liu H J 2023 Multimed. Tools Appl. 82 27973
Google Scholar
[9] Cao Y F, Liu H J 2024 Multimed. Tools Appl. 83 79377
Google Scholar
[10] Zhu P X, Yang Q G 2023 Proc. Am. Math. Soc. 151 5353
Google Scholar
[11] 王兴元, 王明军 2007 56 6843
Google Scholar
Wang X Y, Wang M J 2007 Acta Phys. Sin. 56 6843
Google Scholar
[12] Yang Q G, Zhu P X 2024 Int. J. Bifurcation Chaos 34 2450122
Google Scholar
[13] 赵智鹏, 周双, 王兴元 2021 70 230502
Google Scholar
Zhao Z P, Zhou S, Wang X Y 2021 Acta Phys. Sin. 70 230502
Google Scholar
[14] 扶龙香, 贺少波, 王会海, 孙克辉 2022 71 030501
Google Scholar
Fu L X, He S B, Wang H H, Sun K H 2022 Acta Phys. Sin. 71 030501
Google Scholar
[15] Hua Z Y, Zhang Y X, Bao H, Huang H J, Zhou Y C 2022 IEEE Trans. Circuits Syst. Regul. Pap. 69 784
Google Scholar
[16] Huang L L, Liu J, Xiang J H, Zhang Z F, Du X L 2022 Chaos, Soliton Fractals 160 112248
Google Scholar
[17] Fan C L, Ding Q 2022 Chaos, Soliton Fractals 161 112323
Google Scholar
[18] Zhao M D, Liu H J 2023 Int. J. Bifurcation Chaos 33 2350070
Google Scholar
[19] Zhang Y X, Hua Z Y, Bao H, Huang H J, Zhou Y C 2023 IEEE Trans. Syst. Man Cybern Syst. 53 6516
Google Scholar
[20] Ding D W, Zhu H F, Zhang H W, Yang Z L, Xie D 2024 Chaos, Soliton Fractals 185 115168
Google Scholar
[21] MacQueen J 1967 Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, USA, June 21– July 18 1965 and December 27, 1965–January 7, 1966 p281
[22] Wang C F, Fan C L, Ding Q 2018 Int. J. Bifurcation Chaos 28 1850084
Google Scholar
[23] Termonia Y 1984 Phys. Rev. A 29 1612
Google Scholar
[24] Richman J S, Moorman J R 2000 Am. J. Physiol-Heart C 278 H2039
Google Scholar
[25] Grassberger P, Procaccia I 1983 Phys. Rev. Lett. 50 346
Google Scholar
[26] Zeng J, Wang Y M, Li X Y, Guang Y R, Wang C F, Ding Q 2023 Phys. Scr. 98 075212
Google Scholar
[27] Liu R R, Liu H J, Zhao M D 2023 Integration 93 102071
Google Scholar
[28] Xing Y N, Zeng J, Dong W J, Zhang J, Guo P T, Ding Q 2024 Phys. Scr. 99 035231
Google Scholar
[29] Kumar A, Dua M 2023 Appl. Acoust. 203 109196
Google Scholar
-
图 1 (a) x1 -x2 -x3相图; (b) x4 -x5 -x6相图
Figure 1. (a) x1 -x2 -x3 phase diagram; (b) x4 -x5 -x6 phase diagram.
图 2 分岔图
Figure 2. Bifurcation diagram.
图 3 Lyapunov指数
Figure 3. Lyapunov exponent.
图 4 敏感性分析
Figure 4. Sensitivity analysis
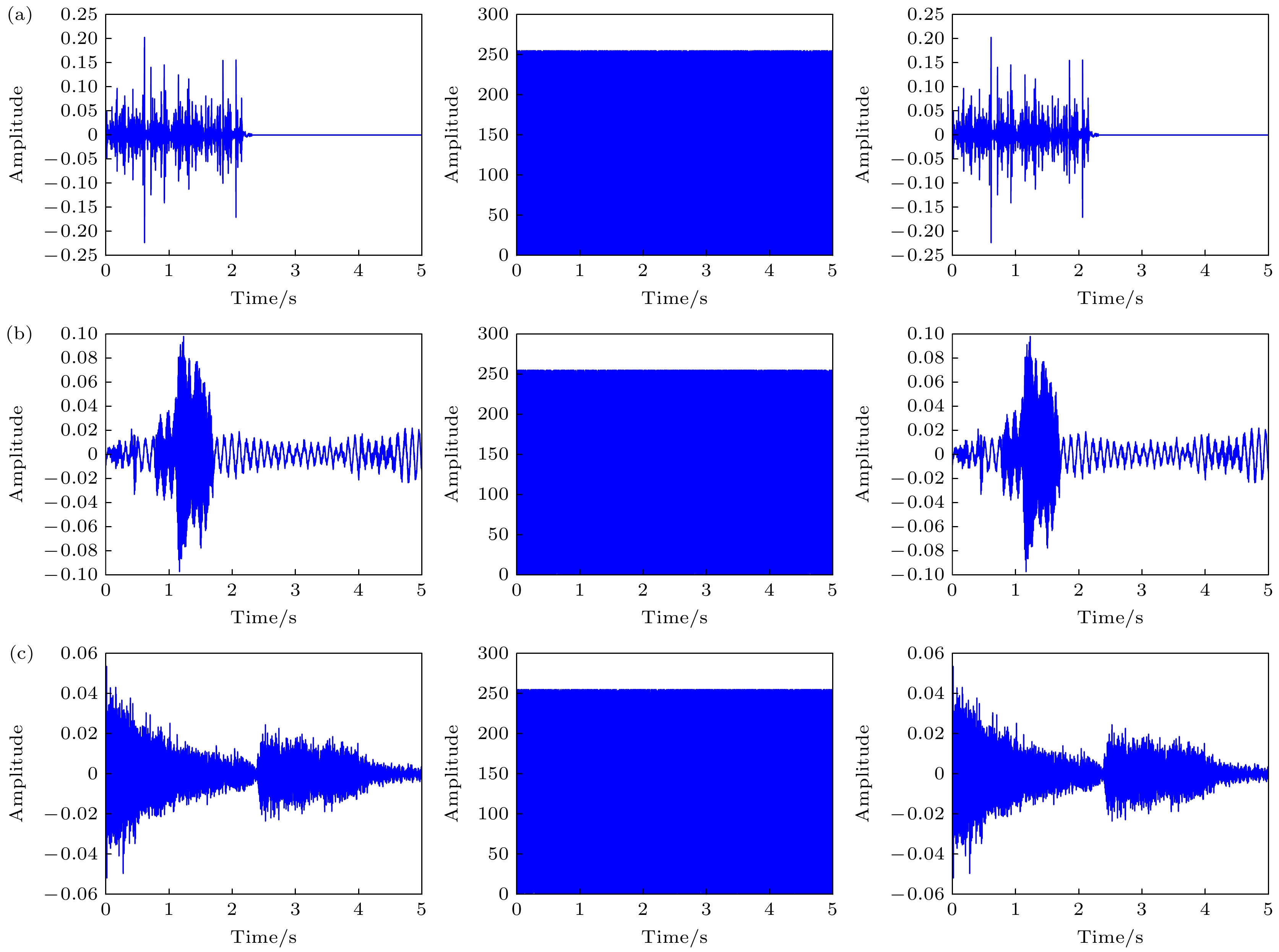
图 5 音频加密与解密仿真(第1列为原始音频波形图; 第2列为加密音频波形图; 第3列为解密音频波形图) (a) 1-67152-A-17.wav的加密与解密; (b) 1-121951-A-8.wav的加密与解密; (c) 5-261464-A-23.wav的加密与解密
Figure 5. Audio encryption and decryption simulation (the first column is the original audio waveform diagram; the second column is an encrypted audio waveform diagram; the third column decrypts the audio waveform diagram): (a) Encryption and decryption of 1-67152-A-17.wav; (b) encryption and decryption of 1-121951-A-8.wav; (c) encryption and decryption of 5-261464-A-23.wav.
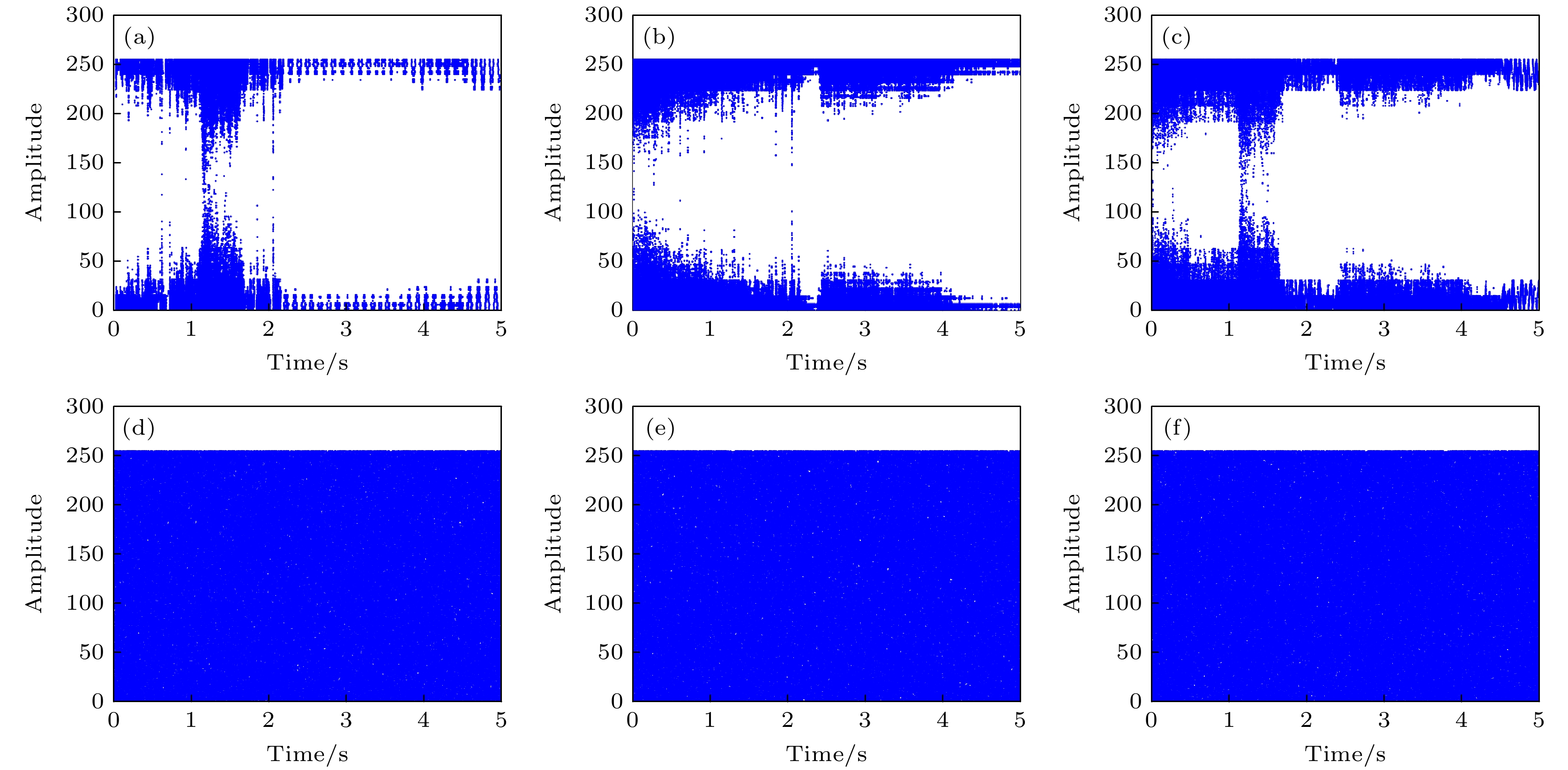
图 6 选择明文攻击 (a) 1-67152-A-17.wav XOR 1-121951-A-8.wav; (b) 5-261464-A-23.wav XOR 1-67152-A-17.wav; (c) 1-121951-A-8.wav XOR 5-261464-A-23.wav; (d) 加密后的 1-67152-A-17.wav XOR加密后的 1-121951-A-8.wav; (e) 加密后的 5-261464-A-23.wav XOR 加密后的1-67152-A-17.wav; (f) 加密后的 1-121951-A-8.wav XOR加密后的 5-261464-A-23.wav
Figure 6. Chosen-plaintext attack: (a) 1-67152-A-17.wav XOR 1-121951-A-8.wav; (b) 5-261464-A-23.wav XOR 1-67152-A-17.wav; (c) 1-121951-A-8.wav XOR 5-261464-A-23.wav; (d) encrypted 1-67152-A-17.wav XOR encrypted 1-121951-A-8.wav; (e) Encrypted 5-261464-A-23.wav XOR Encrypted 1-67152-A-17.wav; (f) encrypted 1-121951-A-8.wav XOR encrypted 5-261464-A-23.wav.
表 1 不同方法的时间复杂度对比
Table 1. Comparison of time complexity of different methods.
离散混沌系统 元素加法个数 矩阵乘法复杂度 算法时间复杂度 Wang et al., 2018[22] $n(n - 1)$ $O({n^3})$ $O({n^3})$ Hua et al., 2022[15] ${{n(n - 1)}}/{2}$ $O({n^3})$ $O({n^3})$ Fan et al., 2022[17] $n(n-1)$ $O({n^3})$ $O({n^3})$ Liu et al., 2023[18] ${{n(n - 1)}}/{2}$ $O({n^3})$ $O({n^3})$ 本文方法 $ 3n-4 \; ({b_i} \ne 0)$
$ 2 n - 4\; ({b_i}=0)$无 $O(n)$ 
DownLoad: CSV
表 2 不同维度下各个变量动力学指标平均值分析
Table 2. Analysis of average dynamic indicators of variables across different dimensions.
维度 KE SE CD 3 0.4312 2.0120 2.1857 4 0.4212 2.0446 2.8712 5 0.4320 2.0973 2.2378 6 0.4226 2.9321 2.7423
DownLoad: CSV
表 3 不同6D混沌系统的6个变量平均值对比
Table 3. Comparison of average values of six variables across different 6D chaotic systems.
DownLoad: CSV
表 4 TestU01测试结果(未通过的数量)
Table 4. TestU01 test results (number of failures).
变量(增益1015) $ {x_1} $ $ {x_2} $ $ {x_3} $ $ {x_4} $ $ {x_5} $ $ {x_6} $ SmallCrush(15) 0 0 0 0 2 0 Crush(144) 6 4 7 6 78 4
DownLoad: CSV
表 5 原始音频相关系数
Table 5. Correlation coefficients of original audio files.
音频 明文 $ A_{n}, A_{n+1} $ $ A_{n}, A_{n+2} $ $ A_{n}, A_{n+3} $ 1-67152-A-17.wav 0.8980 0.6885 0.5066 1-121951-A-8.wav 0.9695 0.8840 0.7583 5-261464-A-23.wav 0.9559 0.8041 0.6811 平均 0.9411 0.7922 0.6487
DownLoad: CSV
表 6 加密音频相关系数
Table 6. Correlation coefficients of encrypted audio files.
音频 密文 $ A_{n}, A_{n+1} $ $ A_{n}, A_{n+2} $ $ A_{n}, A_{n+3} $ 1-67152-A-17.wav –0.0029 –0.0036 0.0011 1-121951-A-8.wav –0.0017 0.0017 –0.0013 5-261464-A-23.wav 0.0020 0.0019 0.0027 绝对值平均 0.0022 0.0024 0.0017
DownLoad: CSV
表 7 加密音频相关系数对比
Table 7. Comparison of correlation coefficients of encrypted audio files.
DownLoad: CSV
表 8 加密音频的信息熵
Table 8. Information entropy of encrypted audio files
音频 明文 密文 1-67152-A-17.wav 1.0577 7.9993 1-121951-A-8.wav 1.9480 7.9993 5-261464-A-23.wav 1.3021 7.9993 平均 1.4359 7.9993
DownLoad: CSV
表 9 加密效率
Table 9. Encryption efficiency.
音频 大小 加密时间/s 速度/(s·KB–1) 1-67152-A-17.wav 430 0.2809 0.00065 1-121951-A-8.wav 430 0.2097 0.00048 5-261464-A-23.wav 430 0.2167 0.00050 平均 430 0.2357 0.00054
DownLoad: CSV
-
[1] Herbadji D, Herbadji A, haddad I, Kahia H, Belmeguenai A, Derouiche N 2024 Integration 97 102192
Google Scholar
[2] Joshi A B, Gaffar A 2024 Soft Comput. 28 5523
Google Scholar
[3] Yu F, Yu Q L, Chen H F, Kong X X, Molbel A A M, Cai S, Du S C 2022 Fractal Fract. 6 370
Google Scholar
[4] Wu R, Gao S, Wang X Y, Liu S B, Li Q, Erkan U, Tang X L 2022 Chaos, Soliton Fractals 165 112770
Google Scholar
[5] Wu R, Gao S, Iu H H, Zhou S, Erkan U, Toktas A, Tang X 2024 IEEE Internet Things J. 11 10214
Google Scholar
[6] Rahul B, Kuppusamy K, Senthilrajan A 2023 Multimed. Tools Appl. 82 43729
Google Scholar
[7] Demirtaş M 2023 Orclever Proc. Res. Dev. 2 28
Google Scholar
[8] Liu H J 2023 Multimed. Tools Appl. 82 27973
Google Scholar
[9] Cao Y F, Liu H J 2024 Multimed. Tools Appl. 83 79377
Google Scholar
[10] Zhu P X, Yang Q G 2023 Proc. Am. Math. Soc. 151 5353
Google Scholar
[11] 王兴元, 王明军 2007 56 6843
Google Scholar
Wang X Y, Wang M J 2007 Acta Phys. Sin. 56 6843
Google Scholar
[12] Yang Q G, Zhu P X 2024 Int. J. Bifurcation Chaos 34 2450122
Google Scholar
[13] 赵智鹏, 周双, 王兴元 2021 70 230502
Google Scholar
Zhao Z P, Zhou S, Wang X Y 2021 Acta Phys. Sin. 70 230502
Google Scholar
[14] 扶龙香, 贺少波, 王会海, 孙克辉 2022 71 030501
Google Scholar
Fu L X, He S B, Wang H H, Sun K H 2022 Acta Phys. Sin. 71 030501
Google Scholar
[15] Hua Z Y, Zhang Y X, Bao H, Huang H J, Zhou Y C 2022 IEEE Trans. Circuits Syst. Regul. Pap. 69 784
Google Scholar
[16] Huang L L, Liu J, Xiang J H, Zhang Z F, Du X L 2022 Chaos, Soliton Fractals 160 112248
Google Scholar
[17] Fan C L, Ding Q 2022 Chaos, Soliton Fractals 161 112323
Google Scholar
[18] Zhao M D, Liu H J 2023 Int. J. Bifurcation Chaos 33 2350070
Google Scholar
[19] Zhang Y X, Hua Z Y, Bao H, Huang H J, Zhou Y C 2023 IEEE Trans. Syst. Man Cybern Syst. 53 6516
Google Scholar
[20] Ding D W, Zhu H F, Zhang H W, Yang Z L, Xie D 2024 Chaos, Soliton Fractals 185 115168
Google Scholar
[21] MacQueen J 1967 Proceedings of the 5th Berkeley Symposium on Mathematical Statistics and Probability, USA, June 21– July 18 1965 and December 27, 1965–January 7, 1966 p281
[22] Wang C F, Fan C L, Ding Q 2018 Int. J. Bifurcation Chaos 28 1850084
Google Scholar
[23] Termonia Y 1984 Phys. Rev. A 29 1612
Google Scholar
[24] Richman J S, Moorman J R 2000 Am. J. Physiol-Heart C 278 H2039
Google Scholar
[25] Grassberger P, Procaccia I 1983 Phys. Rev. Lett. 50 346
Google Scholar
[26] Zeng J, Wang Y M, Li X Y, Guang Y R, Wang C F, Ding Q 2023 Phys. Scr. 98 075212
Google Scholar
[27] Liu R R, Liu H J, Zhao M D 2023 Integration 93 102071
Google Scholar
[28] Xing Y N, Zeng J, Dong W J, Zhang J, Guo P T, Ding Q 2024 Phys. Scr. 99 035231
Google Scholar
[29] Kumar A, Dua M 2023 Appl. Acoust. 203 109196
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 449
- PDF Downloads: 38
- Cited By: 0
