Production of single charm pentaquark based on molecular configuration

Xing Ye; Li Na; Yang Ling-Bin; Hu Xiao-Hui

doi:10.7498/aps.73.20240447

Abstract

In this work, the authors use the effective Lagrangian method to investigate the production of singly charm pentaquark state with spin parity $J ^ P={1/2}^{-} $. Based on the possible molecular state images of hadrons, the author discusses the production of singly charm pentaquark state ${c\bar suud}$ and decuplet baryon $\bar \varDelta$ by $B_{\mathrm{s}}$ meson with different molecular state configurations of $ND_{\mathrm{s}} $ or $ND ^ * _{\mathrm{s}} $. To determine the coupling between pentaquark and their constituents in the molecular scheme, the authors follow the Weinberg compositeness condition to estimate the self-energy diagram of the singly charmed pentaquark. Further study on the production of pentaquark from $B_{\mathrm{s}}$ meson can be propeled by computing the transition matrix elements, or the triangle diagrams, which can be careful divided into two part subprocess, one associated with weak transition can be represented into form factor and decay constant, another one related to strong coupling of hadrons can be described by effective Lagrangian. Selecting the scale parameter α (10–200 MeV) and binding energy ε (5, 20, 50 MeV), the authors can find the branching ratio of the production $\bar B_{\mathrm{s}} \to P_ {{\mathrm{c}}\bar {{\mathrm{s}}}}\bar \varDelta $. Under the configuration of $ND_{\mathrm{s}}$ molecule, the branching ratio of the Cabibbo allowed process $\bar B_{\mathrm{s}} \rightarrow P_{{{\mathrm{c}} \bar{{\mathrm{s}}}}} \bar \varDelta$ can reach to order of $10^{-5}$. Moreover, the production branching ratio of $ND^*_{\mathrm{s}}$ molecule is only at the order of $10^{-8}$. A increasing scale parameter α can significantly improve the production branching ratio of the singly charm pentaquark. In addition, the binding energy and the coupling constants will also affect the magnitude of production. Therefore, considering the above factors, the production branching ratio of singly charm pentaquark in $B_{\mathrm{s}}$ decays have considerable results, which is worth experimental and theoretical research in the future. The findings of our work can provide a reference for the experimental search and study of singly charm pentaquark, and it is hoped that they will be verified in future experimental detections at B factories such as LHCb, Belle, and BaBar.

Keywords:

Authors and contacts

School of Materials Science and Physics, China University of Mining and Technology, Xuzhou 221116, China

Corresponding author: Li Na, TS22180005A31@cumt.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 12005294).

FullText HTML

References

[1]	Aaij R, Advea B, Adinolfi M, et al. 2015 Phys. Rev. Lett. 115 072001 Google Scholar
[2]	Aaij R, Abellán Beteta C, Adeva B, et al. 2019 Phys. Rev. Lett. 122 222001 Google Scholar
[3]	Aaij R, Abellán Beteta C, Ackernley T, et al. 2021 Sci. Bull. 66 1278 Google Scholar
[4]	Aaij R, Abdelmotteleb A S W, Abellán Beteta C, et al. 2022 Phys. Rev. Lett. 128 062001 Google Scholar
[5]	Santopinto E, Giachino A 2017 Phys. Rev. D 96 014014 Google Scholar
[6]	Deng C R, Ping J L, Huang H X, Wang F 2017 Phys. Rev. D 95 014031 Google Scholar
[7]	Azizi K, Sarac Y, Sundu H 2023 Phys. Rev. D 107 014023 Google Scholar
[8]	Chen R, Liu X, Li X Q, Zhu S L 2015 Phys. Rev. Lett. 115 132002 Google Scholar
[9]	Guo F K, Meißner Ulf-G, Wang W, Yang Z 2015 Phys. Rev. D 92 071502 Google Scholar
[10]	Branz T, Gutsche T, Lyubovitskij V E 2021 Phys. Rev. D 104 114028 Google Scholar
[11]	Lebed R F, Martinez S R 2022 Phys. Rev. D 106 074007 Google Scholar
[12]	Zhang Y, He G Z, Ye Q X, Y D C, Hua J, Wang Q 2024 Chin. Phys. Lett. 41 021301 Google Scholar
[13]	Chen H X, Chen W Z, Shi L 2019 Phys. Rev. D 100 051501 Google Scholar
[14]	Liu M Z, Pan Y W, Peng F Z, Sánchez Sánchez M, Geng L S, Hosaka A, Pavon V M 2019 Phys. Rev. Lett. 122 242001 Google Scholar
[15]	Zhu J T, Kong S Y, He J 2023 Am. Phys. Soc. 107 034029 Google Scholar
[16]	Wu Q, Chen D Y 2019 Phys. Rev. D 100 114002 Google Scholar
[17]	Peng F Z, Yan M J, Sánchez Sánchez M, Valderrama M P 2021 Eur. Phys. J. C 81 666 Google Scholar
[18]	Xiao C W, Wu J J, Zou B S 2021 Phys. Rev. D 103 054016 Google Scholar
[19]	Lu J X, Liu M Z, Shi R X, Geng L S 2021 Phys. Rev. D 104 034022 Google Scholar
[20]	Wu Q, Chen D Y, Ji R 2021 Chin. Phys. Lett. 38 071301 Google Scholar
[21]	叶全兴, 何广朝, 王倩 2023 72 201401 Google Scholar Ye Q X, He G C, Wang Q 2023 Acta Phys. Sin. 72 201401 Google Scholar
[22]	Shi P P, Baru Vadim, Guo F K, Hanhart C, Nefediev A 2024 Chin. Phys. Lett. 41 031301 Google Scholar
[23]	Li N, Xing Y, Hu X H 2023 Eur. Phys. J. C 83 1013 Google Scholar
[24]	Huang Y, Xiao C J, Lü Q F, Wang R, He J, Geng L S 2018 Phys. Rev. D 97 094013 Google Scholar
[25]	Zhu H Q, Ma N N, Huang Y 2020 Eur. Phys. J. C 80 1184 Google Scholar
[26]	Yan Y, Hu X H, Huang H X, Ping J L 2023 Phys. Rev. D 108 094045 Google Scholar
[27]	Xin Q, Yang X, Wang Z G 2023 Int. J. Mod. Phys. A 38 2350123 Google Scholar
[28]	Yan M J, Peng F Z, Pavon V M 2024 Phys. Rev. D 109 014023 Google Scholar
[29]	Steven W 1963 Phys. Rev. 130 776 Google Scholar
[30]	Tanja B, Thomas G, Valery E L 2009 Phys. Rev. D 79 014035 Google Scholar
[31]	Xiao C J, Huang Y, Dong Y B, Geng L S, Chen D Y 2019 Phys. Rev. D 100 014022 Google Scholar
[32]	Shen C W, Wu J J, Zou B S 2019 Phys. Rev. D 100 056006 Google Scholar
[33]	Yalikun N, Zou B S 2022 Phys. Rev. D 105 094026 Google Scholar
[34]	McLean E, Davies C T H, Koponen J, Lytle A T 2020 Phys. Rev. D 101 074513 Google Scholar
[35]	Harrison J D, Christine T H 2022 Phys. Rev. D 105 094506 Google Scholar
[36]	Heng H Y 1997 Phys. Rev. D 56 2799 Google Scholar
[37]	Thomas G, Mikhail A I, Jürgen G K, et al. 2015 Phys. Rev. D 91 074001 Google Scholar
[38]	Wu S M, Wang F, Zou B S 2023 Phys. Rev. C 108 045201 Google Scholar
[39]	Li H N, Lu C D, Yu F S 2012 Phys. Rev. D 86 036012 Google Scholar
[40]	Xing Y, Xing Z P 2019 Chin. Phys. C 43 073103 Google Scholar
[41]	Xu Y J, Cui C Y, Liu Y L, Huang M Q 2020 Phys. Rev. D 102 034028 Google Scholar

Cited By

图 1 具有$ ND^{(*)}_{\mathrm{s}} $分子态构型的单粲味五夸克态的自能图

Figure 1. Self-energy diagram of singly charm pentaquark as hadronic molecules $ ND^{(*)}_{\mathrm{s}} $.

DownLoad: Full-Size Img PowerPoint

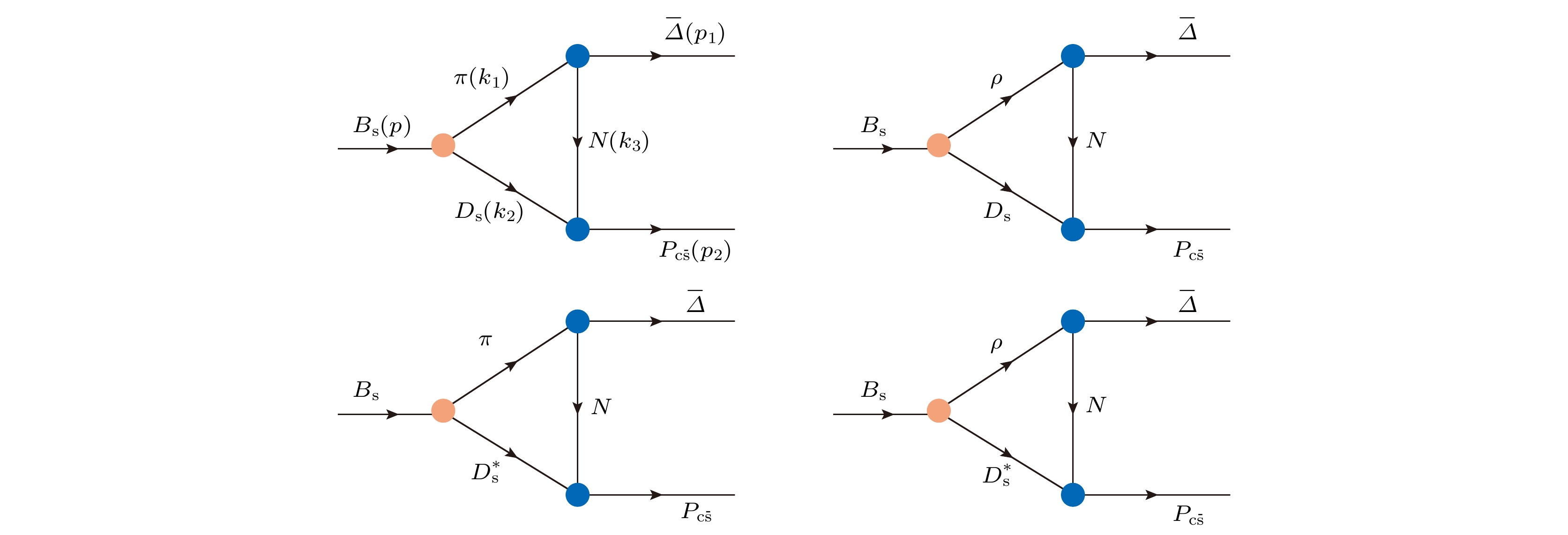
图 2 $ \bar B_{\mathrm{s}} $介子产生单粲五夸克的三角图　(a), (b)具有$ ND_{\mathrm{s}} $分子态构型的单粲五夸克; (c), (d) 具有$ ND^*_{\mathrm{s}} $分子态构型的单粲五夸克

Figure 2. Triangle diagrams of singly charm pentaquark produced by $ \bar B_{\mathrm{s}} $ meson: (a), (b) Singly charm pentaquark with $ ND_{\mathrm{s }}$ molecular state configuration; (c), (d) singly charm pentaquark with $ ND^*_{\mathrm{s}} $ molecular state configuration.

DownLoad: Full-Size Img PowerPoint

图 3 $ \bar B_{\mathrm{s}} $介子弱衰变过程的W发射图

Figure 3. W emission diagram of $ \bar B_{\mathrm{s}} $ meson weak decay

DownLoad: Full-Size Img PowerPoint

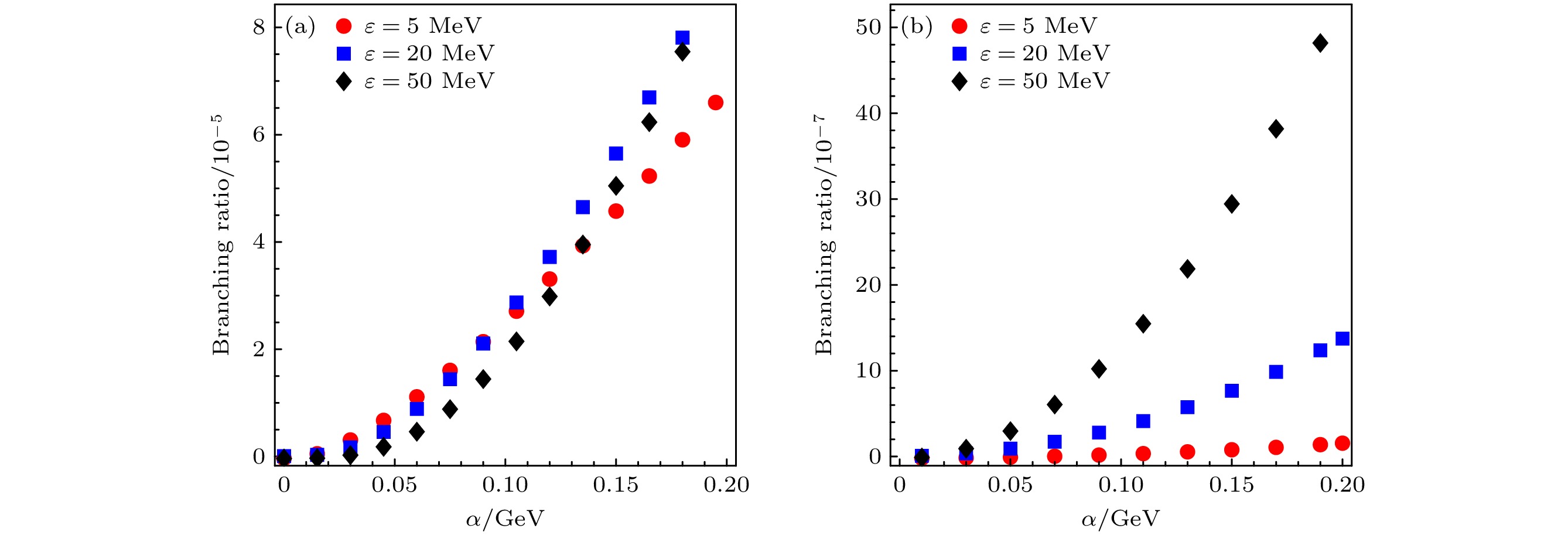
图 4 $ \bar B_{\mathrm{s}} \xrightarrow[]{N} P_{{\mathrm{c}} \bar{{\mathrm{s}}}} \bar \varDelta $的分支比随参数α的变化曲线　(a) $ P_{{\mathrm{c}} \bar{{\mathrm{s}}}} $为$ ND_{\mathrm{s}} $分子态; (b) $ P_{{\mathrm{c}} \bar{{\mathrm{s}}}} $为$ N{D^*_{\mathrm{s}}} $分子态

Figure 4. Branching ratios of $ \bar B_{\mathrm{s}} \xrightarrow[]{N} P_{{\mathrm{c}} \bar{{\mathrm{s}}}} \bar \varDelta $ vary with the parameter α: (a) $ P_{{\mathrm{c}} \bar{{\mathrm{s}}}} $ as hadronic molecule $ ND_{\mathrm{s}} $; (b) $ P_{{\mathrm{c}} \bar{{\mathrm{s}}}} $ as hadronic molecule $ ND^*_{\mathrm{s}} $

DownLoad: Full-Size Img PowerPoint

表 1 形状因子$ F_{1}(k^2) $, $ F_{2}(k^2) $和$ A_i(k^2) $(i = 1, 2, 3)的拟合展开参数$ a_i $和$ m_{{\mathrm{pole}}} $^[34,35]

Table 1. Fitted parameters $ a_i $ and pole mass $ m_{{\mathrm{pole}}} $ of form factors $ F_{1}(k^2) $, $ F_{2}(k^2) $ and $ A_i(k^2) $(i = 1, 2, 3)^[34,35].

参数	$ {\bar B_{\mathrm{s}}\to D} $		$ {\bar B_{\mathrm{s}}\to D^*} $
参数	$ F_1(k_1) $	$ F_2(k_1) $	$ A_{0}(k_1) $	$ A_{1}(k_1) $	$ A_{2}(k_1) $	$ A_{3}(k_1) $
$ a_{0} $	$ 0.666 $	$ 0.666 $	$ 0.100 $	$ 0.105 $	$ 0.055 $	$ 0.059 $
$ a_{1} $	$ -0.206 $	$ -3.236 $	$ -0.180 $	$ -0.430 $	$ -0.010 $	$ -0.110 $
$ a_{2} $	$ -0.106 $	$ -0.075 $	$ -0.006 $	$ -0.100 $	$ -0.030 $	$ -0.250 $
$ a_{3} $	$ 0.00 $	$ -0.00 $	$ 0.00 $	$ -0.030 $	$ 0.060 $	$ -0.050 $
$ m_{{\mathrm{pole}}} $/GeV	$ — $	$ — $	$ 6.335 $	$ 6.275 $	$ 6.745 $	$ 6.745 $

DownLoad: CSV

表 2 单粲味五夸克态的产生分支比(α = 100 MeV)

Table 2. Production branching ratio of singly charm pentaquark state (α = 100 MeV).

分子态	产生道	分支比($ \times 10^{-6} $)
		$ \varepsilon $/MeV
		5	20	50
$ ND_{\mathrm{s}} $	$ \bar B_{\mathrm{s}} \xrightarrow[]{N} P_{{\mathrm{c}} \bar{{\mathrm{s}}}} \bar \varDelta $	29.40	31.37	24.51
$ ND_{\mathrm{s}} $	$ \bar B_{\mathrm{s}}\xrightarrow[]{N} P_{{\mathrm{c}} \bar{{\mathrm{s}}}}(\to \varLambda_{\mathrm{c}} K) \bar \varDelta $	0.223	0.194	0.137
$ ND^*_{\mathrm{s}} $	$ \bar B_{\mathrm{s}}\xrightarrow[]{N} P_{{\mathrm{c}} \bar{{\mathrm{s}}}} \bar \varDelta $	0.055	0.408	1.570
	$ \bar B_{\mathrm{s}}\xrightarrow[]{N} P_{{\mathrm{c}} \bar{{\mathrm{s}}}}(\to \varLambda_{\mathrm{c}} K) \bar \varDelta $	0.0006	0.0041	0.0157
	$ \bar B_{\mathrm{s}}\xrightarrow[]{N} P_{{\mathrm{c}} \bar{{\mathrm{s}}}}(\to \Sigma_{\mathrm{c}} K) \bar \varDelta $	0.0004	0.0024	0.0072
	$ \bar B_{\mathrm{s}}\xrightarrow[]{N} P_{{\mathrm{c}} \bar{{\mathrm{s}}}}(\to p D_{\mathrm{s}}) \bar \varDelta $	0.0002	0.0015	0.0050

DownLoad: CSV

map

[1]	Aaij R, Advea B, Adinolfi M, et al. 2015 Phys. Rev. Lett. 115 072001 Google Scholar
[2]	Aaij R, Abellán Beteta C, Adeva B, et al. 2019 Phys. Rev. Lett. 122 222001 Google Scholar
[3]	Aaij R, Abellán Beteta C, Ackernley T, et al. 2021 Sci. Bull. 66 1278 Google Scholar
[4]	Aaij R, Abdelmotteleb A S W, Abellán Beteta C, et al. 2022 Phys. Rev. Lett. 128 062001 Google Scholar
[5]	Santopinto E, Giachino A 2017 Phys. Rev. D 96 014014 Google Scholar
[6]	Deng C R, Ping J L, Huang H X, Wang F 2017 Phys. Rev. D 95 014031 Google Scholar
[7]	Azizi K, Sarac Y, Sundu H 2023 Phys. Rev. D 107 014023 Google Scholar
[8]	Chen R, Liu X, Li X Q, Zhu S L 2015 Phys. Rev. Lett. 115 132002 Google Scholar
[9]	Guo F K, Meißner Ulf-G, Wang W, Yang Z 2015 Phys. Rev. D 92 071502 Google Scholar
[10]	Branz T, Gutsche T, Lyubovitskij V E 2021 Phys. Rev. D 104 114028 Google Scholar
[11]	Lebed R F, Martinez S R 2022 Phys. Rev. D 106 074007 Google Scholar
[12]	Zhang Y, He G Z, Ye Q X, Y D C, Hua J, Wang Q 2024 Chin. Phys. Lett. 41 021301 Google Scholar
[13]	Chen H X, Chen W Z, Shi L 2019 Phys. Rev. D 100 051501 Google Scholar
[14]	Liu M Z, Pan Y W, Peng F Z, Sánchez Sánchez M, Geng L S, Hosaka A, Pavon V M 2019 Phys. Rev. Lett. 122 242001 Google Scholar
[15]	Zhu J T, Kong S Y, He J 2023 Am. Phys. Soc. 107 034029 Google Scholar
[16]	Wu Q, Chen D Y 2019 Phys. Rev. D 100 114002 Google Scholar
[17]	Peng F Z, Yan M J, Sánchez Sánchez M, Valderrama M P 2021 Eur. Phys. J. C 81 666 Google Scholar
[18]	Xiao C W, Wu J J, Zou B S 2021 Phys. Rev. D 103 054016 Google Scholar
[19]	Lu J X, Liu M Z, Shi R X, Geng L S 2021 Phys. Rev. D 104 034022 Google Scholar
[20]	Wu Q, Chen D Y, Ji R 2021 Chin. Phys. Lett. 38 071301 Google Scholar
[21]	叶全兴, 何广朝, 王倩 2023 72 201401 Google Scholar Ye Q X, He G C, Wang Q 2023 Acta Phys. Sin. 72 201401 Google Scholar
[22]	Shi P P, Baru Vadim, Guo F K, Hanhart C, Nefediev A 2024 Chin. Phys. Lett. 41 031301 Google Scholar
[23]	Li N, Xing Y, Hu X H 2023 Eur. Phys. J. C 83 1013 Google Scholar
[24]	Huang Y, Xiao C J, Lü Q F, Wang R, He J, Geng L S 2018 Phys. Rev. D 97 094013 Google Scholar
[25]	Zhu H Q, Ma N N, Huang Y 2020 Eur. Phys. J. C 80 1184 Google Scholar
[26]	Yan Y, Hu X H, Huang H X, Ping J L 2023 Phys. Rev. D 108 094045 Google Scholar
[27]	Xin Q, Yang X, Wang Z G 2023 Int. J. Mod. Phys. A 38 2350123 Google Scholar
[28]	Yan M J, Peng F Z, Pavon V M 2024 Phys. Rev. D 109 014023 Google Scholar
[29]	Steven W 1963 Phys. Rev. 130 776 Google Scholar
[30]	Tanja B, Thomas G, Valery E L 2009 Phys. Rev. D 79 014035 Google Scholar
[31]	Xiao C J, Huang Y, Dong Y B, Geng L S, Chen D Y 2019 Phys. Rev. D 100 014022 Google Scholar
[32]	Shen C W, Wu J J, Zou B S 2019 Phys. Rev. D 100 056006 Google Scholar
[33]	Yalikun N, Zou B S 2022 Phys. Rev. D 105 094026 Google Scholar
[34]	McLean E, Davies C T H, Koponen J, Lytle A T 2020 Phys. Rev. D 101 074513 Google Scholar
[35]	Harrison J D, Christine T H 2022 Phys. Rev. D 105 094506 Google Scholar
[36]	Heng H Y 1997 Phys. Rev. D 56 2799 Google Scholar
[37]	Thomas G, Mikhail A I, Jürgen G K, et al. 2015 Phys. Rev. D 91 074001 Google Scholar
[38]	Wu S M, Wang F, Zou B S 2023 Phys. Rev. C 108 045201 Google Scholar
[39]	Li H N, Lu C D, Yu F S 2012 Phys. Rev. D 86 036012 Google Scholar
[40]	Xing Y, Xing Z P 2019 Chin. Phys. C 43 073103 Google Scholar
[41]	Xu Y J, Cui C Y, Liu Y L, Huang M Q 2020 Phys. Rev. D 102 034028 Google Scholar

[1]	Chu Peng-Cheng, Liu He, Du Xian-Bin. Quark matter and quark star in color-flavor-locked phase. Acta Physica Sinica, 2024, 73(5): 052101. doi: 10.7498/aps.73.20231649
[2]	Song Tong-Tong, Luo Jie, Lai Yun. Pseudo-local effect medium theory. Acta Physica Sinica, 2020, 69(15): 154203. doi: 10.7498/aps.69.20200196
[3]	Zhai Han-Yu, Shen Jia-Yin, Xue Xun. Effective quintessence from string landscape. Acta Physica Sinica, 2019, 68(13): 139501. doi: 10.7498/aps.68.20190282
[4]	Qin Chao-Chao, Huang Yan, Peng Yu-Feng. Photodissociation dynamics of Br2 in wavelength range of 360-610 nm. Acta Physica Sinica, 2017, 66(19): 193301. doi: 10.7498/aps.66.193301
[5]	Li Qiong, Shen Li, Yan Jun-Gang, Dai Chang-Jian, Yang Yu-Na. Dynamic properties of Eu 4f76p1/2ns autoionization process. Acta Physica Sinica, 2016, 65(15): 153202. doi: 10.7498/aps.65.153202
[6]	Liang Hong-Rui, Shen Li, Jing Hua, Dai Chang-Jian. The VMI study on branching ratio decay from Eu 6p1/28s autoionizing state. Acta Physica Sinica, 2014, 63(13): 133202. doi: 10.7498/aps.63.133202
[7]	Jin Zhao, Qiao Li-Ping, Guo Chen, Wang Jiang-An, Richard C. Liu. Electronic conductivity effective masses along arbitrary directional channel in uniaxial strained Si(001). Acta Physica Sinica, 2013, 62(5): 058501. doi: 10.7498/aps.62.058501
[8]	Zhou Wen-Fei, Ye Xiao-Ling, Xu Bo, Zhang Shi-Zhu, Wang Zhan-Guo. Study on properties of the H1 photonic crystal slab cavity using the effective index perturbation method. Acta Physica Sinica, 2012, 61(5): 054202. doi: 10.7498/aps.61.054202
[9]	Zhang Bing-Xin, Liu Xiao-Jing, Zhang Bai-Jun, Hua Zhong, Xiao Li, Liu Bing, Wu Yi-Heng, Wang Qing-Cai, Wang Yan. Research on branching ratio of B0→π－l+ν l decay. Acta Physica Sinica, 2011, 60(4): 041301. doi: 10.7498/aps.60.041301
[10]	Zou Xian-Rong, Shao Jian-Xiong, Chen Xi-Meng, Cui Ying. Kβ/Kα ratios and energies of the K-shell X-ray of Ar17+ ion in the interaction with metals. Acta Physica Sinica, 2010, 59(9): 6064-6070. doi: 10.7498/aps.59.6064
[11]	Han Li-Li, Dai Zhen-Wen, Wang Yun-Peng, Jiang Zhan-Kui. Measurement of branching ratios of Pd I. Acta Physica Sinica, 2008, 57(6): 3425-3428. doi: 10.7498/aps.57.3425
[12]	Wu Xiang-Yao, Gong Pi-Feng, Su Xi-Yu, Liu Xiao-Jing, Fan Xi-Hui, Wang Li, Shi Zong-Hua, Guo Yi-Qing. Research on D→Klv～l decay. Acta Physica Sinica, 2006, 55(7): 3375-3379. doi: 10.7498/aps.55.3375
[13]	Lu Di, Yan Xiao-Hong, Ding Jian-Wen. Electron effective mass of single-wall carbon nanotubes. Acta Physica Sinica, 2004, 53(2): 527-530. doi: 10.7498/aps.53.527
[14]	Wu Xiang-Yao, Yin Xin-Guo, Guo Yi-Qing, Zhang Xiao-Bo, Yin Jian-Hua, Xie Yuan-Liang. Research on B0→K0π0 decay. Acta Physica Sinica, 2004, 53(4): 1015-1019. doi: 10.7498/aps.53.1015
[15]	CHEN XIAO-BO, MENG CHAO, WANG YA-FEI, MA HUI, LI MEI-XIAN. POPULATION BRANCHING RATIO MODEL——AN EFFECTIVE QUALITIVE ANALYSIS METHOD ABOUT UP-CONVERSION EFFICIENCY. Acta Physica Sinica, 2000, 49(6): 1176-1179. doi: 10.7498/aps.49.1176
[16]	LI ZI-PING. GLOBAL QUANTAL CANONICAL SYMMETRY PROPERTIES FOR A SYSTEM WITH A SINGULAR LAGRANGIAN. Acta Physica Sinica, 1996, 45(10): 1601-1608. doi: 10.7498/aps.45.1601
[17]	TENG HUA-GUO, SHEN BAI-FEI, ZHANG WEN-QI, XU ZHI-ZHAN. EFFECT OF CONFIGURATION INTERACTION ON THE AUTOIONIZATION RATES AND BRANCH RATIOS OF Na LIKE Cu ION. Acta Physica Sinica, 1994, 43(2): 205-210. doi: 10.7498/aps.43.205
[18]	ZHANG YAO-ZHONG. EFFECTIVE LAGRANGIAN AND MASS GENERATION OF THE CHIRAL QCD2 MODEL. Acta Physica Sinica, 1987, 36(11): 1513-1518. doi: 10.7498/aps.36.1513
[19]	. . Acta Physica Sinica, 1965, 21(11): 1919-1920. doi: 10.7498/aps.21.1919
[20]	TZU PAO-RU. ON THE DECAY BRANCH RATIO OF THE UNSTABLE PARTICLE η:R((η→ππγ)/(η→3π)). Acta Physica Sinica, 1965, 21(1): 92-102. doi: 10.7498/aps.21.92

Catalog

Vol. 73, Issue 13 - 2024-07-05

Metrics

Abstract views: 1808
PDF Downloads: 40
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板