强磁场与有限温度下色味锁夸克星的唯象模型研究

初鹏程; 刘玉珩; 刘鹤; 刘宏铭; 杨永杭

doi:10.7498/aps.74.20250451

摘要
本文基于准粒子模型对强磁场和有限温度下色味锁夸克物质与色味锁磁星的性质进行了讨论. 我们发现色味锁夸克物质的每核子自由能、有效质量、每核子熵等物理量受磁场、温度、能隙常数的影响较大, 并且强磁场、有限温度环境中色味锁夸克物质的压强会产生各向异性. 我们进一步研究了不同等熵阶段下的色味锁磁星的性质, 发现色味锁磁星的质量、半径等性质与磁星内部的磁场强度分布、磁场方向分布紧密相关, 磁星内部温度会随着每核子熵的增加而增大. 结论还表明色味锁夸克物质的多方指数会随着色味锁夸克星质量的增大而减少.

关键词:
色味锁态 /

夸克星 /

磁星
Abstract
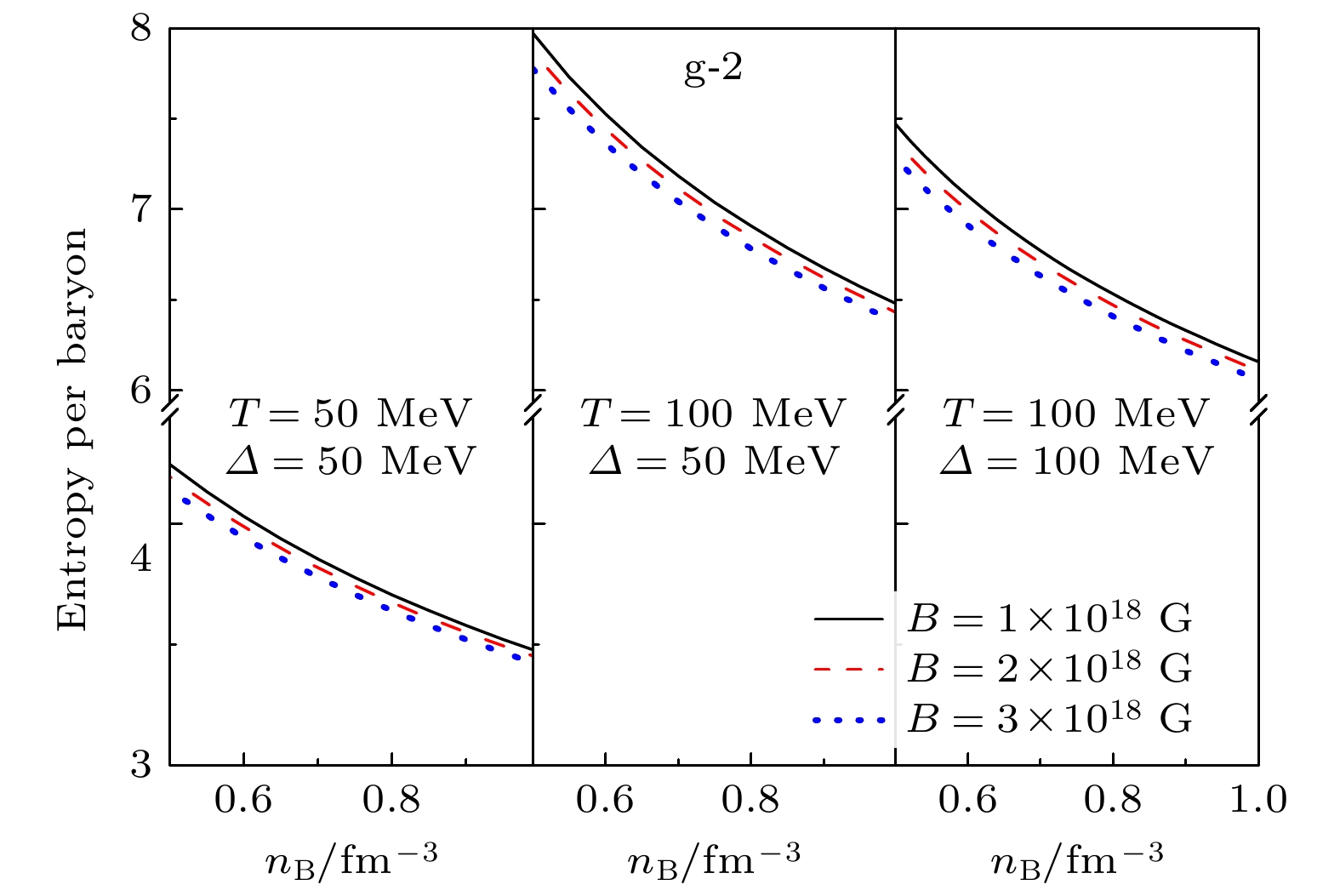
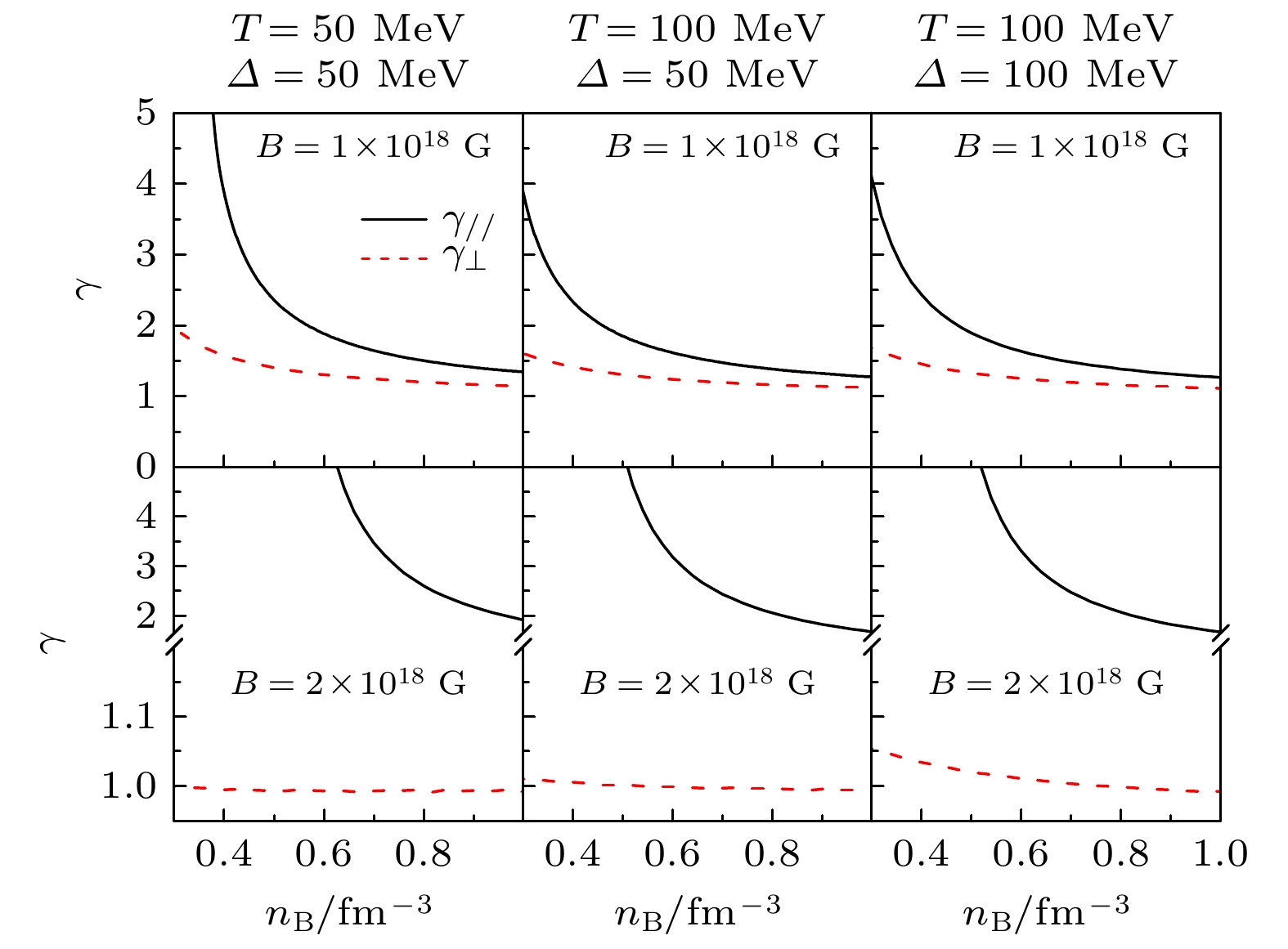
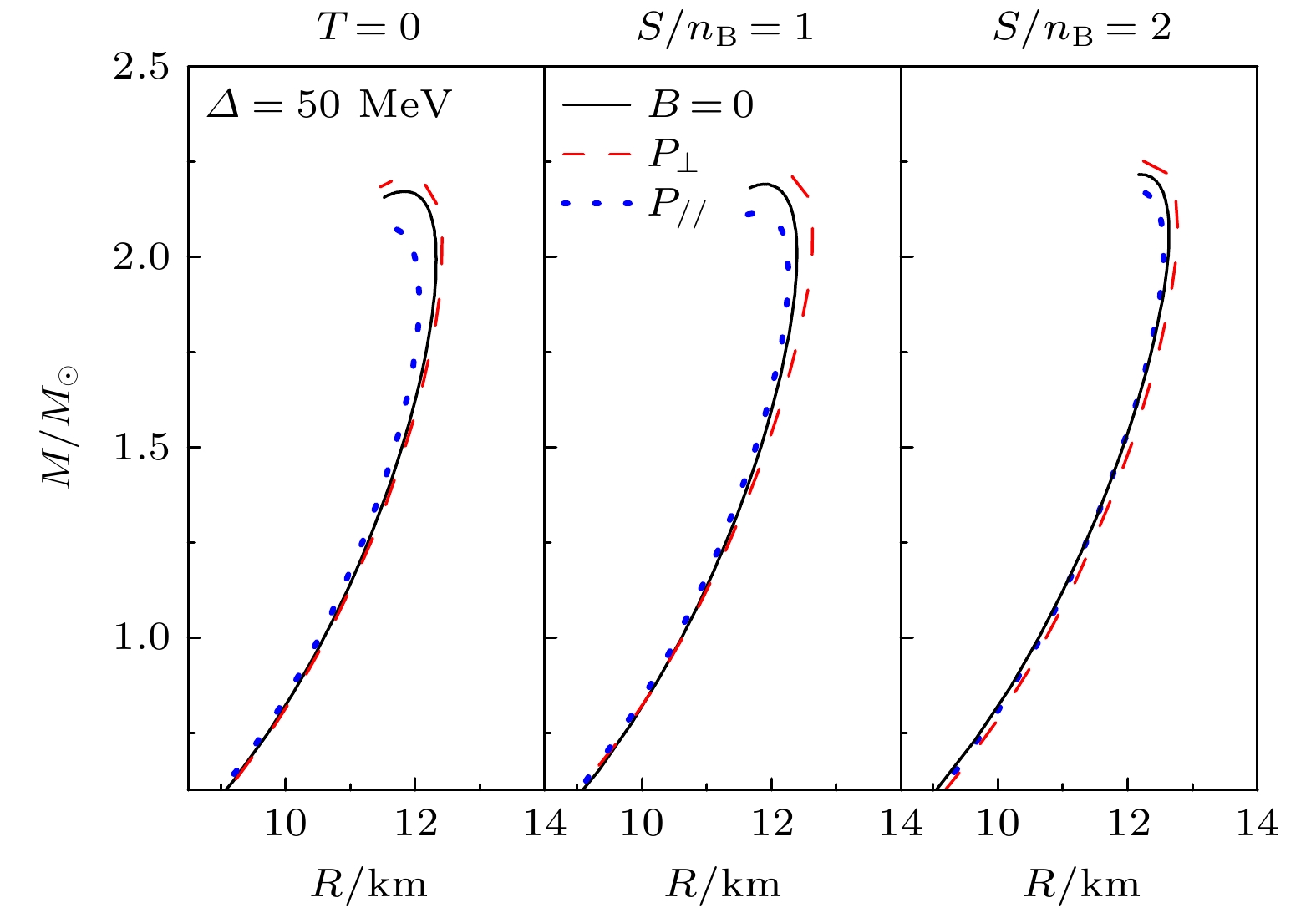
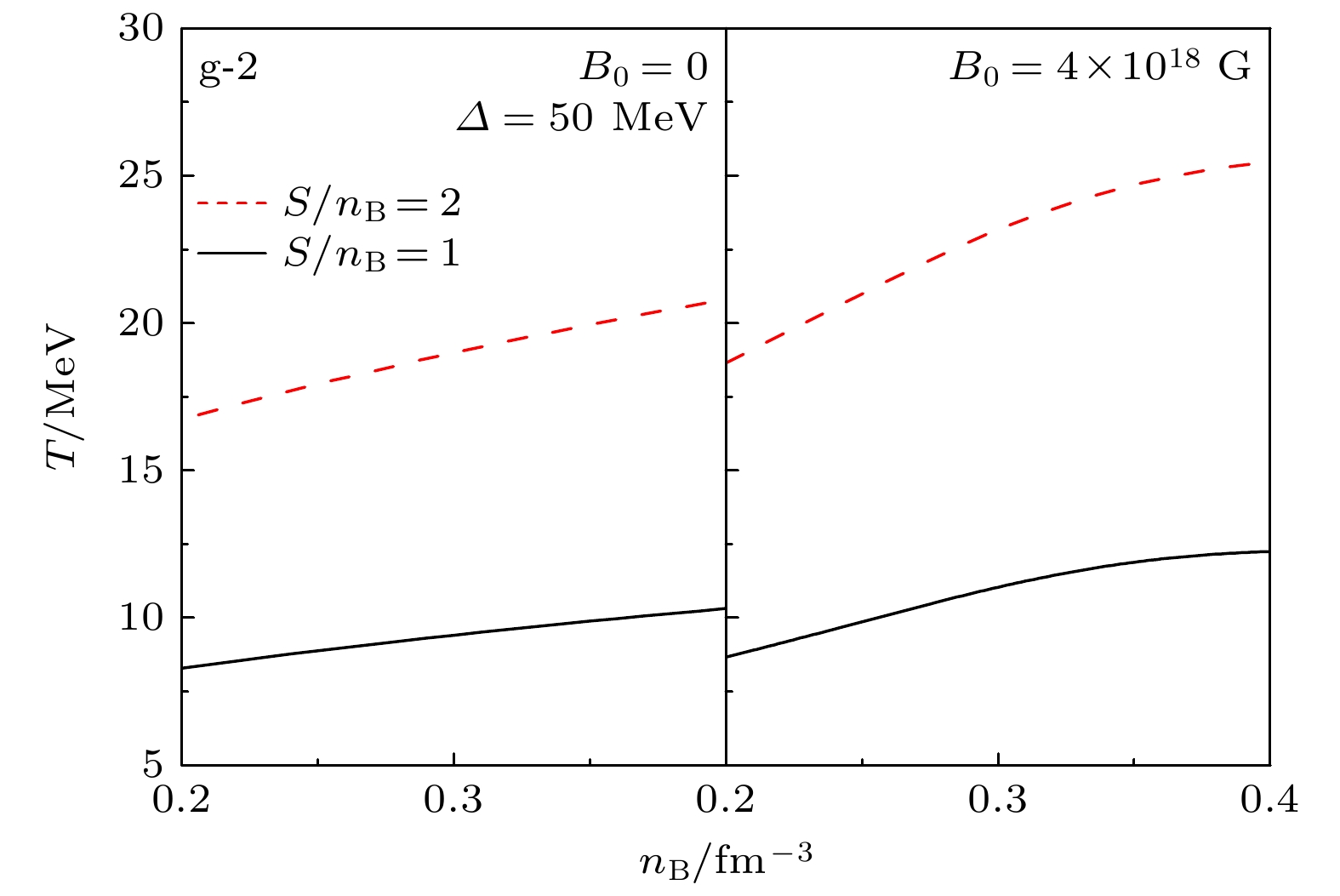
We investigate the properties of the color-flavor-locked (CFL) quark matter at finite temperature and under strong magnetic fields within quasiparticle model. Our results indicate that the pressure of CFL quark matter may become anisotropic under strong magnetic fields, and the equations of state (EOS) and the equivalent quark mass can be strongly influenced by the temperature, the energy gap constat Δ, and the strong magnetic fields inside the CFL quark matter. The equivalent quark mass of CFL quark matter decreases with the increment of the temperature and magnetic field strength, which implies a inverse magnetic catalysis phenomenon. The results also indicate that the entropy per baryon of the CFL quark matter increases with the temperature and decreases with Δ. Furthermore, we study the properties of the CFL magnetars in different isentropic stages, and the results indicate that the star mass and radius is mainly dependent on the strength and orientation distributions of the magnetic field inside the CFL magnetars. The maximum star mass increases with the entropy per baryon, and the temperature of the star matter increases at the large isentropic stages. Moreover, our results also suggest that the polytropic index of the CFL quark matter decrease with the increment of the star mass.

Keywords:
Color-flavor-locked phase /

Quark star /

Magnetar
文章全文

施引文献
图 1 不同温度与能隙常数下色味锁态物质的每核子自由能与横纵向压强随着$ n_B $的变化关系

Fig. 1. The free energy per baryon and pressures of CFL quark matter with $ n_B $ at finite temperature and with different $ \Delta $.

下载: 全尺寸图片幻灯片

图 2 不同温度与能隙常数下u夸克的有效质量随磁感应强度的变化

Fig. 2. The equivalent mass of u quarks as a function of the magnetic field with different temperature and $ \Delta $.

下载: 全尺寸图片幻灯片

图 3 色味锁态下夸克星物质的每核子熵随着不同温度、磁场、能隙常数的变化

Fig. 3. The entropy per baryon of the quark star matter in MCFL state with various temperature, magnetic field, and $ \Delta $.

下载: 全尺寸图片幻灯片

图 4 MCFL下夸克物质的多方指数随磁场、温度、能隙常数的变化规律

Fig. 4. The polytropic index of the MCFL quark star matter as a function of the magnetic field strength, temperature, and $ \Delta $.

下载: 全尺寸图片幻灯片

图 5 不同等熵阶段中的色味锁磁星的质量-半径情况

Fig. 5. The star mass as functions of the radius of the MCFL quark stars along different isentropic stages.

下载: 全尺寸图片幻灯片

图 6 不同等熵阶段下色味锁夸克星内部温度随$ n_B $与磁场的变化

Fig. 6. The temperature of the MCFL quark star matter as functions of $ n_B $ and magnetic field along different isentropic stages.

下载: 全尺寸图片幻灯片

map

[1]	Glendenning N K 2000 Compact Stars (2 nd edition) (New York: Spinger-Verlag, Inc.
[2]	Weber F 1999 Pulsars as Astrophyical Laboratories for Nuclear and Particle Physics (London: IOP Publishing Ltd
[3]	Lattimer J M and Prakash M 2004 Science 304 536 Google Scholar
[4]	Steiner A W, Prakash M, Lattimer J M, Ellis P J 2005 Phys. Rep. 410 325
[5]	Demorest P 2010 Nature 467 1081 Google Scholar
[6]	Antoniadis J 2013 Science 340 6131
[7]	Shahbaz T, Casares J 2018 Astrophys. Journal 859 54 Google Scholar
[8]	Thankful H, Cromartie 2020 Nature Astronomy Letter 4 72
[9]	Fonseca E, et al 2021 Astrophys. J. Lett. 915 L12 Google Scholar
[10]	Miller M C, et al 2021 Astrophys. J. Lett. 918 L28 Google Scholar
[11]	Abbott R 2020 Astrophys. J. Lett. 896 L44 Google Scholar
[12]	Ivanenko D, Kurdgelaidze D F 1969 Lett. Nuovo Cimento 2 13 Google Scholar
[13]	Itoh N 1970 Prog. Theor. Phys. 44 291 Google Scholar
[14]	Bodmer A R 1971 Phys. Rev. D 4 1601 Google Scholar
[15]	Witten E 1984 Phys. Rev. D 30 272 Google Scholar
[16]	Farhi E, Jaffe R L 1984 Phys. Rev. D 30 2379 Google Scholar
[17]	Holdom B, et al 2018 Phys. Rev. L 120 22001 Google Scholar
[18]	Zhang C and Mann R B 2021 Phys. Rev. D 103 063018 Google Scholar
[19]	Li C M, et al 1984 Phys. Rev. D 30 2379 Google Scholar
[20]	Yuan L W, Li A, Miao Z Q, Zuo B J, and Bai Z 1984 Phys. Rev. D 105 123004
[21]	Alcock C, Farh E, Olinto A 1986 Astrophy. J. 310 261 Google Scholar
[22]	Weber F 2005 Prog. Part. Nucl. Phys. 54 193 Google Scholar
[23]	Bombaci I, Parenti I, Vidana I 2004 Astrophy. J. 614 314 Google Scholar
[24]	Staff J, Ouyed R, Bagchi M 2007 Astrophy. J. 667 340 Google Scholar
[25]	Herzog T M, Röpke F K 2011 Phys. Rev. D 84 083002 Google Scholar
[26]	Stephanov M A, Rajagopal K, Shuryak E V 1998 Phys. Rev. Lett. 81 4816 Google Scholar
[27]	Terazawa H 1979 INS-Report (Tokyo: Univ. of Tokyo) 336
[28]	Alford M, Reddy S 2003 Phys. Rev. D 67 074024 Google Scholar
[29]	Alford M, Jotwani P, Kouvaris C, Kundu J, Rajagopal K 2005 Phys. Rev. D 71 114011 Google Scholar
[30]	Baldo M 2003 Phys. Lett. B 562 153 Google Scholar
[31]	Ippolito N D, Ruggieri M, Rischke D H, Sedrakian A, Weber F 2008 Phys. Rev. D 77 023004 Google Scholar
[32]	Lai X Y, Xu R X 2011 Research Astron. Astrophys. 11 687 Google Scholar
[33]	Avellar M G B de, Horvath J E, Paulucci L 2011 Phys. Rev. D 84 043004 Google Scholar
[34]	Bonanno L, Sedrakian A 2012 A&A 539 A16
[35]	Chu P C, Wang B, Jia Y Y, Dong Y M, Wang S M, Li X H, Zhang L, Zhang X M, Ma H Y 2016 Phys. Rev. D 94 123014 Google Scholar
[36]	Chu P C, Li X H, Wang B, Dong Y M, Jia Y Y, Wang S M, Ma H Y 2017 Eur. Phys. J. C 77 512 Google Scholar
[37]	Chu P C, Zhou Y, Chen C, Li X H, Ma H Y 2020 J. Phys. G: Nucl. Part. Phys. 47 085201 Google Scholar
[38]	Bailin D and Love A 1984 Phys. Rept. 107 325 Google Scholar
[39]	Alford M G, Rajagopal K, Reddy S and Wilczek F 2001 Phys. Rev. D 64 074017 Google Scholar
[40]	Shovkovy I A 2005 Found. Phys. 35 1309 Google Scholar
[41]	Rajagopal K and Wilczek F 2001 Phys. Rev. L 86 3492 Google Scholar
[42]	Alford M G, Rajagopal K, Schaefer T and Schmitt A 2008 Rev. Mod. Phys. 80 1455 Google Scholar
[43]	Lugones G and Horvath J E 2003 Astron. Astrophys. 403 173 Google Scholar
[44]	Horvath J E and Lugones G 2004 Astron. Astrophys. 422 L1 Google Scholar
[45]	Li X H, Gao Z F, Li X D, Xu Y, Wang P, WangN, Peng Q H 2016 Int. J. Mod. Phys. D 25 165000
[46]	Gao Z F, Wang N, Shan H, L i, X D, Wang W 2017 Astrophys. J. 849 19 Google Scholar
[47]	Deng Z L, Gao Z F, Li X D, Shao Y 2020 Astrophys. J. 892 4 Google Scholar
[48]	Yan F Z, Gao Z F, Yang W S, Dong A J 2021 Astron. Nachr. 342 249 Google Scholar
[49]	Wang H, Gao Z F, Jia H Y, Wang N, Li X 2020 Universe 6
[50]	Li B P, Gao Z F 2023 Astron. Nachr. 344 e20220111
[51]	Deng Z L, Li X D, Gao Z F, Shao Y 2021 Astrophys. J. 909 174 Google Scholar
[52]	G ao, Z F, Omar N, Shi X C, Wang N 2019 Astron. Nachr. 340 1030 Google Scholar
[53]	Lander, S K 2023 Astrophys.J. 947 L16 Google Scholar
[54]	L Woltjer 1964 Astrophys. J. 140 1309 Google Scholar
[55]	Mihara T A 1990 Nature 346 250 Google Scholar
[56]	Chanmugam G 1992 Annu. Rev. Astron. Astrophys. 30 143 Google Scholar
[57]	Lai D, Shapiro S L 1991 Astrophys. J. 383 745 Google Scholar
[58]	Ferrer E J, Incera V, Keith J P, Portillo I, Springsteen P L 2010 Phys. Rev. C 82 065802
[59]	Bandyopadhyay D, Chakrabarty S, Pal S 1997 Phys Rev. Lett. 79 2176 Google Scholar
[60]	Bandyopadhyay D, Pal S, Chakrabarty S 1998 J. Phys. G: Nucl. Part. Phys. 24 1647 Google Scholar
[61]	Menezes D P, Pinto M, Benghi, Avancini S, Providência C 2009 Phys. Rev. C 79 035807 Google Scholar
[62]	Menezes D P, Pinto M, Benghi, Avancini S, Providência C 2009 Phys. Rev. C 80 065805 Google Scholar
[63]	Ryu C Y, Kim K S, Cheoun Myung-Ki 2010 Phys. Rev. C 82 025804 Google Scholar
[64]	Ryu C Y, Cheoun Myung-Ki, Kajino T, Maruyama T, Mathews Grant J 2012 Astroparticle Physics 38 25 Google Scholar
[65]	Dong J M 2021 Mon. Not. R. Astron. Soc. 500 1505
[66]	Fu G Z, Xing C C, Wang N 2020 Eur. Phys. J. C 80 582 Google Scholar
[67]	Schertler K, Greiner C, Thoma M H, Schertler K, Greiner C, Thoma M H 1997 Nucl. Phys. A 616 659 Google Scholar
[68]	Pisarski R D 1989 Nucl. Phys. A 498 423
[69]	Wen X J 2009 J. Phys. G: Nucl. Part. Phys. 36 025011 Google Scholar
[70]	Zhang Z, Chu P C, Li X H, Liu H, Zhang X M 2021 Phys. Rev. D 103 103021 Google Scholar
[71]	Chu P C, Chen L W 2014 Astrophys. J. 780 135
[72]	Chu P C 2018 Phys. Lett. B 778 447 Google Scholar
[73]	Chu P C, Chen L W 2017 Phys. Rev. D 96 103001 Google Scholar
[74]	Chodos A, Jaffe R L, Ohnson K, Thorn C B, Weisskopf V F 1974 Phys. Rev. D 9 3471 Google Scholar
[75]	Alford M, Braby M, Paris M, Reddy S 2005 Astrophy. J. 629 969 Google Scholar
[76]	Rehberg P, Klevansky S P, Hüfner J 1996 Phys. Rev. C 53 410
[77]	Hanauske M, Satarov L M, Mishustin I N, Stocker H, Greiner W 2001 Phys. Rev. D 64 043005 Google Scholar
[78]	Rüster S B, Rischke D H 2004 Phys. Rev. D 69 045011 Google Scholar
[79]	Menezes D P, Providencia C, Melrose D B 2006 J. Phys. G 32 1081 Google Scholar
[80]	Chao J Y, Chu P C, Huang M 2013 Phys. Rev. D 88 054009 Google Scholar
[81]	Chu P C, Wang X, Chen L W, Huang M 2015 Phys. Rev. D 91 023003, Chu P C et al. 2024 Acta Phys. Sin. 73, 052101.
[82]	Chu P C, Wang B, Ma H Y, Dong Y M, Chang S L, Zheng C H, Liu J T, Zhang X M 2016 Phys. Rev. D 93 094032 Google Scholar
[83]	Chu P C, Chen L W 2017 Phys. Rev. D 96 083019 Google Scholar
[84]	Roberts C D, Williams A G 1994 Prog. Part. Nucl. Phys. 33 477 Google Scholar
[85]	Zong H S, Chang L, Hou F Y, Sun W M, Liu Y X 2005 Phys. Rev. C 71 015205 Google Scholar
[86]	Peng G X, Chiang H C, Yang J J, Li L, Liu B 1999 Phys. Rev. C 61 015201 Google Scholar
[87]	Peng G X, Chiang H C, Zou B S, Ning P Z, Luo S J 2000 Phys. Rev. C 62 025801
[88]	Peng G X, Li A, Lombardo U 2008 Phys. Rev. C 77 065807 Google Scholar
[89]	Li A, Peng G X, Lu J F 2011 Research Astron. Astrophys. 11 482 Google Scholar
[90]	Schertler K, Greiner C, Thoma M H 1997 Nucl. Phys. 659
[91]	Schertler K, Greiner C, Sahu P K, Thoma M H 1998 Nucl. Phys. A 637 451 M. Alford, C. Kouvaris, and K. Rajagopal, PRD 71, 054009 (2005
[92]	Alford M, Kouvaris C, Rajagopal K 2005 Phys. Rev. D 71 054009 Google Scholar
[93]	Ioannis Giannakis, et al 2004 Phys. Rev. L 93 232301 Google Scholar
[94]	Dong A.J., et al 2023 Acta Phys. Sin. 72 030502 Google Scholar
[95]	Ferrer E J and Vivian de la Incera 2005 Phys. Rev. Lett. 95 152002 Google Scholar
[96]	Ferrer E J, Vivian de la Incera, Cristina Manuel 2006 Nucl.Phys. B 747 88 Google Scholar
[97]	Feng B, Ferrer E J, and Vivian de la Incera 2011 Nucl.Phys. B 853 213 Google Scholar
[98]	Paulucci L, Ferrer E J, Vivian de la Incera, and Horvath J E 2011 Phys. Rev. D 83 043009 Google Scholar
[99]	Isayev A A, Yang J 2011 Phys. Rev. C 84 065802
[100]	Isayev A A, Yang J 2012 Phys. lett. B 707 163 Google Scholar
[101]	Isayev A A, Yang J 2013 J. Phys. G: Nucl. Part. Phys. 40 035105 Google Scholar
[102]	Feng B, Hou D F, Ren H C, and Wu P P 2010 Phys. Rev. L 105 042001 Google Scholar
[103]	Gao Z F, Li X D, Wang N, Yuan J P, Wang P, Peng Q H, Du Y J 2016 Mon. Not. R. Astron. Soc. 456 55 Google Scholar
[104]	Gao Z F, Wang N, Peng Q H, Li X D, Du Y J 2013 Mod. Phys. Lett A 28 1350138
[105]	Dong A J, et al 2013 Acta Phys. Sin. 72 030502
[106]	Oppenheimer J R, and Volkoff G M 1939 Phys. Rev. 33 374
[107]	Chu P C, Chen L W, Wang X 2014 Phys. Rev. D 90 063013 Google Scholar
[108]	Chu P C, Liu H, Liu H M, Ju M, Wu X H, Zhou Y, and Li X H 2025 Eur. Phys. J. C 85 466 Google Scholar
[109]	Chu P C, Liu H, Liu H M, Li X H, Ju M, Wu X H, and Zhou Y 2024 Phys. Rev. D 110 123031 Google Scholar
[110]	Chu P C, Liu H, Ju M, Wu X H, Liu H M, Zhou Y, Liu H, Lu S Y, and Li X H 2024 Phys. Rev. D 110 043032, Chu P C, Liu H, Li X H, Ju M, Wu X H, and Zhang X M 2024 J. Phys. G: Nucl. Part. Phys. 51 065202

[1]	李丹, 刘海峰. 中国首台准环对称仿星器中线圈形变对磁拓扑结构的影响. , doi: 10.7498/aps.74.20241606
[2]	徐建峰, 王靖涛, 夏铖君. 新质量标度下u-d夸克星与其潮汐形变的研究. , doi: 10.7498/aps.74.20250535
[3]	邢晔, 李娜, 杨翎彬, 胡晓会. 基于分子态构型研究单粲味五夸克态的产生. , doi: 10.7498/aps.73.20240447
[4]	初鹏程, 刘鹤, 杜先斌. 色味锁夸克物质与夸克星. , doi: 10.7498/aps.73.20231649
[5]	苏祥, 王先驱, 符添, 许宇鸿. CFQS准环对称仿星器低$\boldsymbol \beta$等离子体中三维磁岛的抑制机制. , doi: 10.7498/aps.72.20230546
[6]	董爱军, 高志福, 杨晓峰, 王娜, 刘畅, 彭秋和. 在超强磁场中修正的相对论电子压强. , doi: 10.7498/aps.72.20220092
[7]	王谊农, 初鹏程, 姜瑶瑶, 庞晓迪, 王圣博, 李培新. 基于准粒子模型的原生磁星研究. , doi: 10.7498/aps.71.20220795
[8]	龚武坤, 郭文军. 混合中子星内强子-夸克退禁闭相变. , doi: 10.7498/aps.69.20200925
[9]	陈建玲, 王辉, 贾焕玉, 马紫微, 李永宏, 谭俊. 超强磁场下中子星壳层的电导率和磁星环向磁场欧姆衰变. , doi: 10.7498/aps.68.20190760
[10]	吉日木图, 敖登, 薛康. 坐标空间中构造的Breit夸克势与介子和夸克偶素的质量劈裂. , doi: 10.7498/aps.67.20172155
[11]	刘向远, 钱仙妹, 朱文越, 刘丹丹, 范传宇, 周军, 杨欢. 基于波长330 nm激光激发多色激光导星回波光子数的数值计算与探讨. , doi: 10.7498/aps.67.20171025
[12]	黄金书, 罗鹏晖, 鲁公儒. 关于光子对撞机上底夸克对产生的研究. , doi: 10.7498/aps.58.8166
[13]	赖祥军, 罗志全, 刘晶晶, 刘宏林. 超新星核中的夸克相变及夸克质量效应. , doi: 10.7498/aps.57.1535
[14]	陈　洪, 梅　花, 沈彭年, 姜焕清. 重夸克偶素质量谱的相对论夸克模型研究（已撤稿）. , doi: 10.7498/aps.54.1136
[15]	戴子高, 陆埮. 奇异星的冷却. , doi: 10.7498/aps.43.198
[16]	戴子高, 陆埮, 彭秋和. 中子星内部非奇异-奇异夸克物质的相变. , doi: 10.7498/aps.42.1210
[17]	谢凤仙. t夸克偶素能谱的计算. , doi: 10.7498/aps.36.778
[18]	王青德, 陆埮. π凝聚态中的弱过程对中子星振动的阻尼效应. , doi: 10.7498/aps.34.892
[19]	何祚庥, 林大航, 赵培贞. 考虑胶子质量的重夸克偶素位模型. , doi: 10.7498/aps.31.525
[20]	王家珠, 毕品镇, 殷鹏程. 重夸克对强子的椭球袋模型. , doi: 10.7498/aps.30.1707

计量

文章访问数: 228
PDF下载量: 10
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

强磁场与有限温度下色味锁夸克星的唯象模型研究

Properties of color-flavor-locked quark star at finite temperature and under strong magnetic fields

摘要

Abstract

文章全文

施引文献

计量

作者中心

审稿中心

关于期刊

关于我们

搜索

留言板

强磁场与有限温度下色味锁夸克星的唯象模型研究

Properties of color-flavor-locked quark star at finite temperature and under strong magnetic fields

摘要

Abstract

文章全文

施引文献

计量

出版历程

作者中心

审稿中心

关于期刊

关于我们