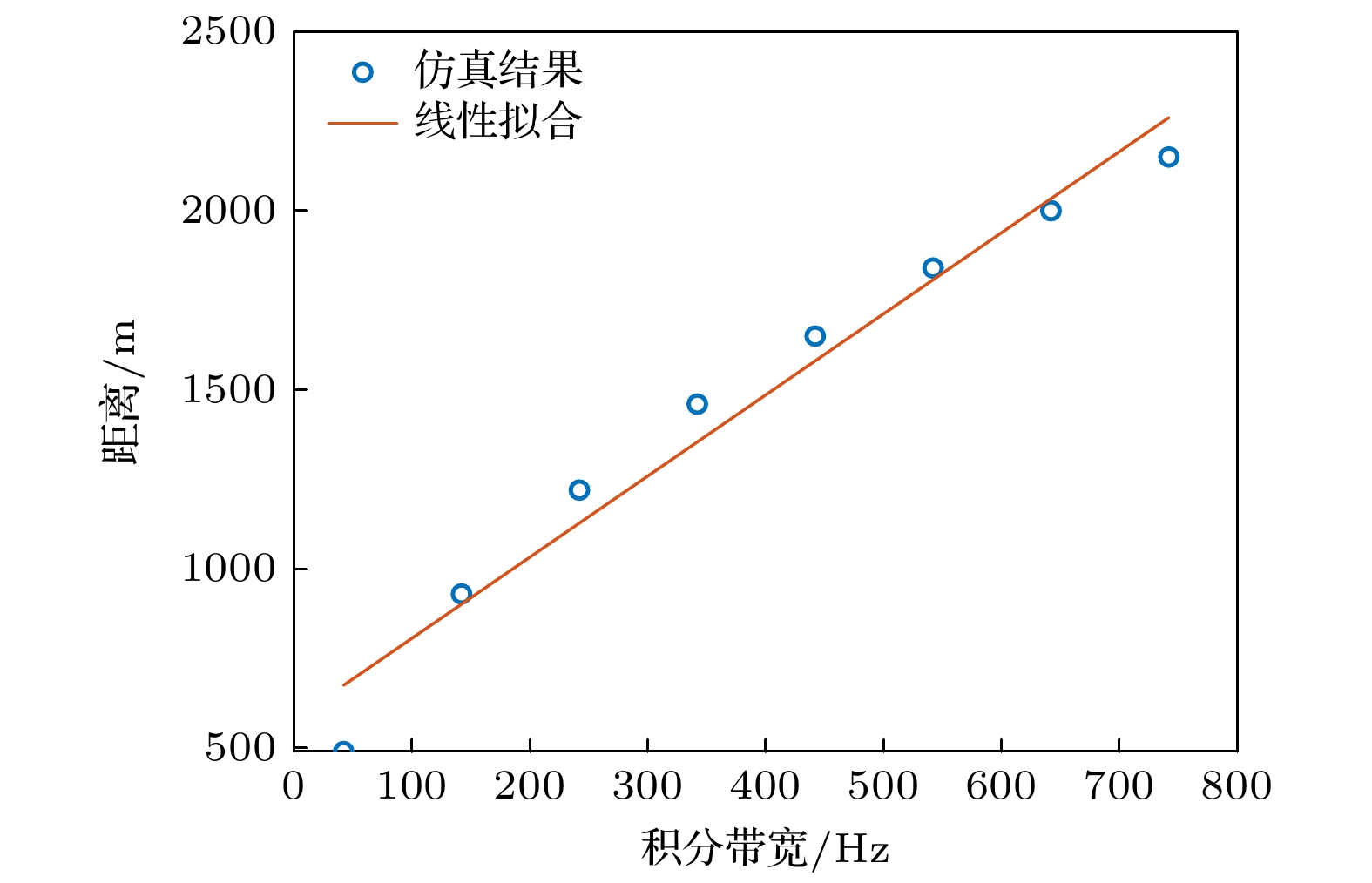
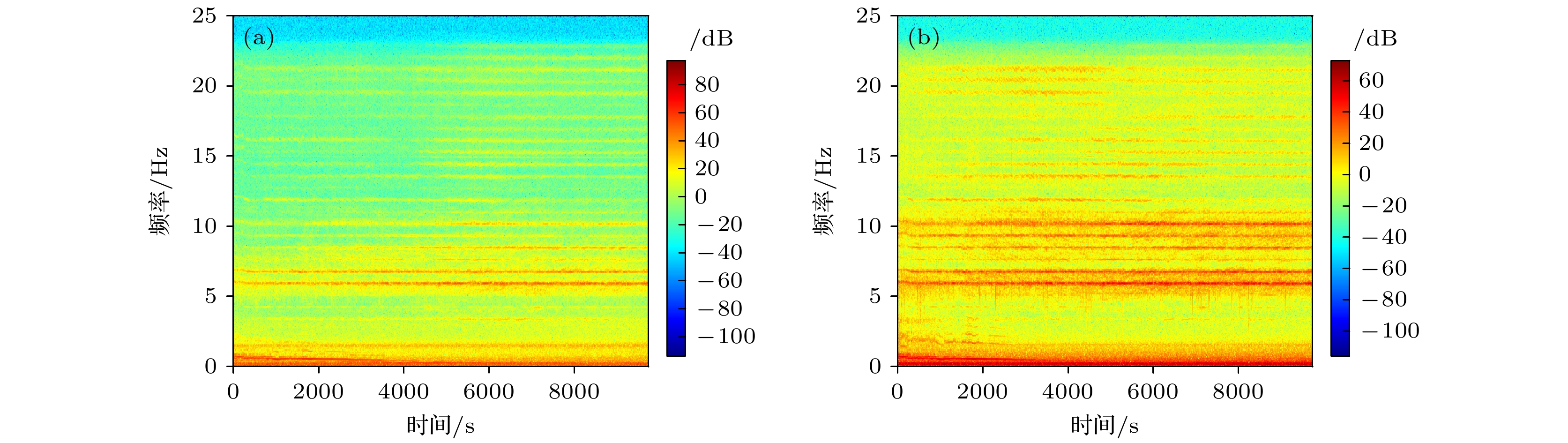
-
The polarization of the acoustic field in the ocean waveguide environment is a unique property that can be measured by using a particle velocity sensor in the water column. It can provide new ideas for locating and detecting the underwater target, so it is interesting to study the polarization. The polarization of a monochromatic signal has been described by the Stokes parameters, a set of four real-valued quantities in previous work. In this work, the Stokes parameters are extended to the broadband form, and the expression is simplified by using the nonstationary phase approximation, which reduces the complexity of the theoretical derivation and reveals the physical mechanism behind the significant variations in polarization with source depth and symmetrical depth. Theoretical analysis shows that the polarization characteristics in the ideal waveguide vary significantly in the sea surface, the sea bottom, the depth of the sound source and symmetrical depth. In this work the numerical simulation is used to verify the theoretical analysis and study the relationship between range and integral bandwidth when nonstationary phase approximation method is effective. The numerical results demonstrate that the simplified expression using the nonstationary phase approximation is effective and can better characterize the depth distribution characteristics of the polarization. Additionally, by normalizing the broadband Stokes parameters, the effect of range on the depth distribution characteristics of polarization can be removed. It means that the normalized broadband Stokes parameters are in theory free of the range and depend on the environment, the receiver depth and the source depth, which have the potential to be used for source depth estimation. Subsequently, focusing on normalized broadband Stokes parameters, we analyzes the effects of parameters such as source frequency, source depth, sound speed profile and water depth on the depth distribution characteristics of polarization. The analysis results show that environmental factors have great influence on the depth distribution characteristics of polarization. In the end, the validity of the nonstationary phase approximation and the range-independent property of the normalized broadband Stokes parameters are verified by the results of the RHUM-RUM experimental data processing. The findings provide a theoretical basis for passive target depth estimation based on polarization.
-
Keywords:
- polarization /
- vector acoustic field /
- shallow sea /
- Stokes parameters
Retraction of article: Depth distribution law of polarization characteristics of vector acoustic field in shallow sea[ 2022, 73(10): 247502]
Wei Yi-Zheng, Sun Chao, Zhu Qi-Xuan. Retraction of article: Depth distribution law of polarization characteristics of vector acoustic field in shallow sea. , 2024, 73(10): 247502. doi: 10.7498/aps.73.109902
[1] 休罗夫V 著 (贾志富 译) 2011 海洋矢量声学(北京: 国防工业出版社)第2—5页
Shchurov V (translated by Jia Z F) 2011 Vector Acoustics of the Ocean (Beijing: National Defense Industry Press) pp2–5
[2] 姜哲, 郭骅 1991 声学学报 16 330
Google Scholar
Jiang Z, Guo H 1991 Acta Acust. 16 330
Google Scholar
[3] Li J F, Pascal J C, Carles C 1998 J. Acoust. Soc. Am. 103 962
Google Scholar
[4] Shi C, Zhao R, Long Y, Yang S, Wang Y, Chen H, Ren J, Zhang X 2019 Natl. Sci. Rev. 6 707
Google Scholar
[5] Bliokh K Y, Nori F 2019 Phys. Rev. B 99 020301
Google Scholar
[6] Long Y, Ge H, Zhang D, Xu X, Ren J, Lu M H, Bao M, Chen H, Chen Y F 2020 Natl. Sci. Rev. 7 1024
Google Scholar
[7] Long Y, Zhang D, Yang C, Ge J, Chen H, Ren J 2020 Nat. Commun. 11 4716
Google Scholar
[8] Shchurov V A, Kuleshov V P, Cherkasov A V 2011 Acoust. Phys. 57 851
Google Scholar
[9] D’Spain G L, Hodgkiss W S 1991 J. Acoust. Soc. Am. 90 2300
Google Scholar
[10] Dall'Osto D R, Dahl P H 2013 J. Acoust. Soc. Am. 134 109
Google Scholar
[11] Dahl P H, Dall'Osto D R 2020 IEEE J. Oceanic Eng. 45 131
Google Scholar
[12] Dahl P H, Dall'Osto D R 2021 IEEE J. Oceanic Eng. 47 680
Google Scholar
[13] 刘伟 2014 博士学位论文 (哈尔滨: 哈尔滨工程大学)
Liu W 2014 Ph. D. Dissertation (Harbin: Harbin Engineering University
[14] Du B, Zhang W, Shi X 2016 IEEE/OES China Ocean Acoustics (COA) Harbin, China, August 8, 2016 pp1−3
[15] 韩雪 2020 博士学位论文 (哈尔滨: 哈尔滨工程大学)
Han X 2020 Ph. D. Dissertation (Harbin: Harbin Engineering University
[16] Bonnel J, Flamant J, Dall'Osto D R, Le Bihan N, Dahl P H 2021 J. Acoust. Soc. Am. 150 1897
Google Scholar
[17] 玻恩M, 沃尔夫 E 著 (杨葭荪 译) 2016 光学原理: 光的传播、干涉和衍射的电磁理论(北京: 电子工业出版社)第20—27页
Born M, Wolf E (translated by Yang J S) 2016 Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (Beijing: Publishing House of Electronics Industry) pp20–27
[18] Dahl P H, Bonnel J 2022 J. Acoust. Soc. Am. 151 3818
Google Scholar
[19] Dahl P H, Dall'Osto D R, Hodgkiss W S 2023 J. Acoust. Soc. Am. 154 1482
Google Scholar
[20] Flamant J, Bonnel J 2023 J. Acoust. Soc. Am. 153 3012
Google Scholar
[21] 延森 F B, 库珀曼 W A, 波特 M B, 施米特 H 著 (周利生, 王鲁军, 杜栓平 译) 2017 计算海洋声学 (第2版) (北京: 国防工业出版社)第272—275页
Jensen F B, Kuperman W A, Porter M B, Schmidt H (translated by Zhou L S, Wang L J, Du S P) 2017 Computational Ocean Acoustics (2nd Ed.) (Beijing: National Defense Industry Press) pp272–275
[22] Tsekhmistrenko M, Sigloch K, Hosseini K, Barruol G 2021 Nat. Geosci. 14 612
Google Scholar
[23] Trabattoni A, Barruol G, Dréo R, Boudraa A 2023 J. Acoust. Soc. Am. 153 260
Google Scholar
-
图 1 横波的极化现象 (a) 线极化; (b) 圆极化; (c) 椭圆极化
Figure 1. Polarization of transverse wave: (a) Linear polarization; (b) circular polarization; (c) elliptical polarization.
图 2 质点椭圆运动轨迹
Figure 2. Elliptical path of acoustic particle motion.
图 3 归一化Stokes参数与极化状态的关系
Figure 3. Relation between normalized Stokes parameters and polarization states.
图 4 $ {D_N}(z) $随$z$变化曲线
Figure 4. Curve of $ {D_N}(z) $ with $z$.
图 5 $ {E_N}(z) $随$z$变化曲线
Figure 5. Curve of $ {E_N}(z) $ with z.
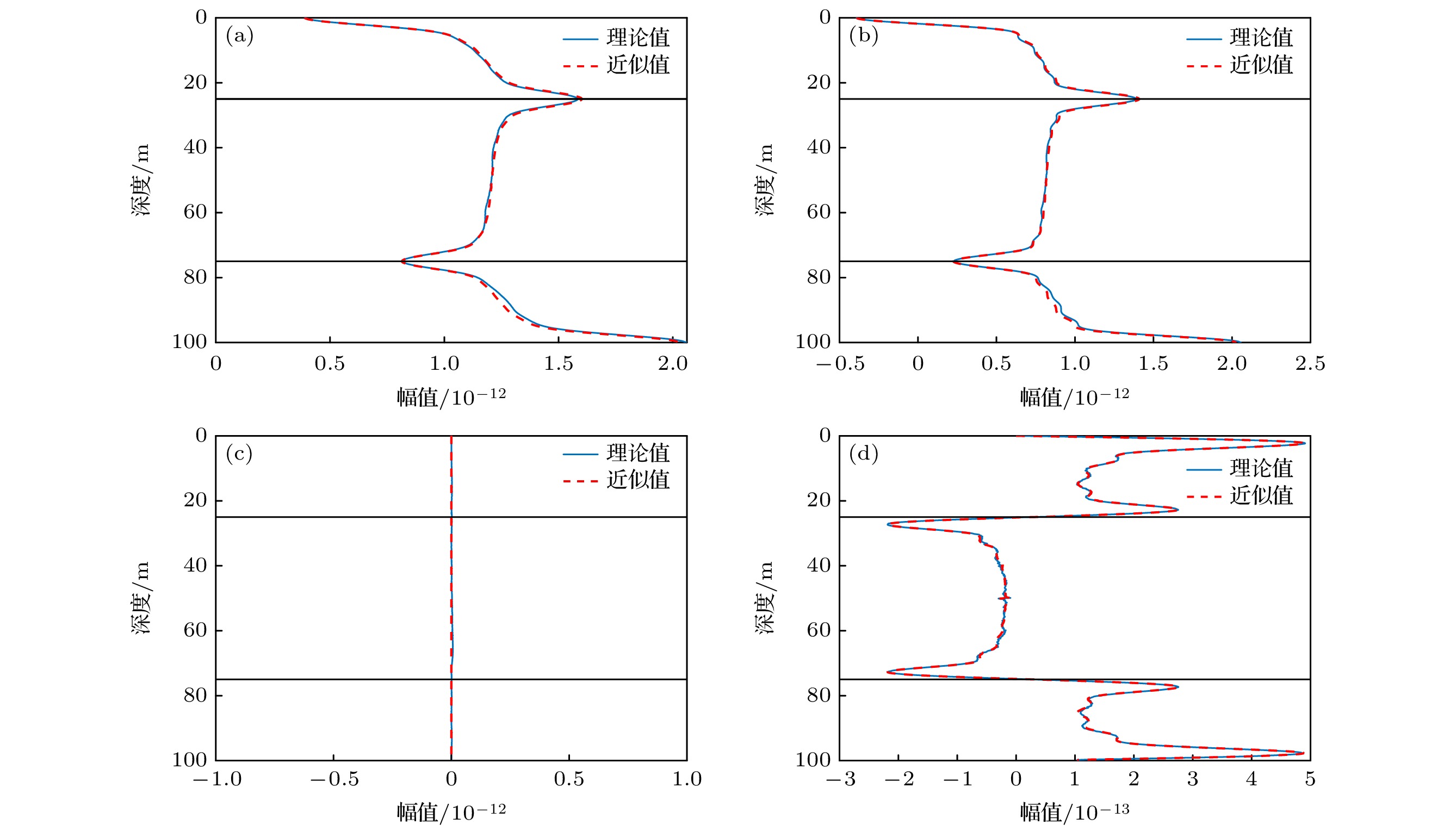
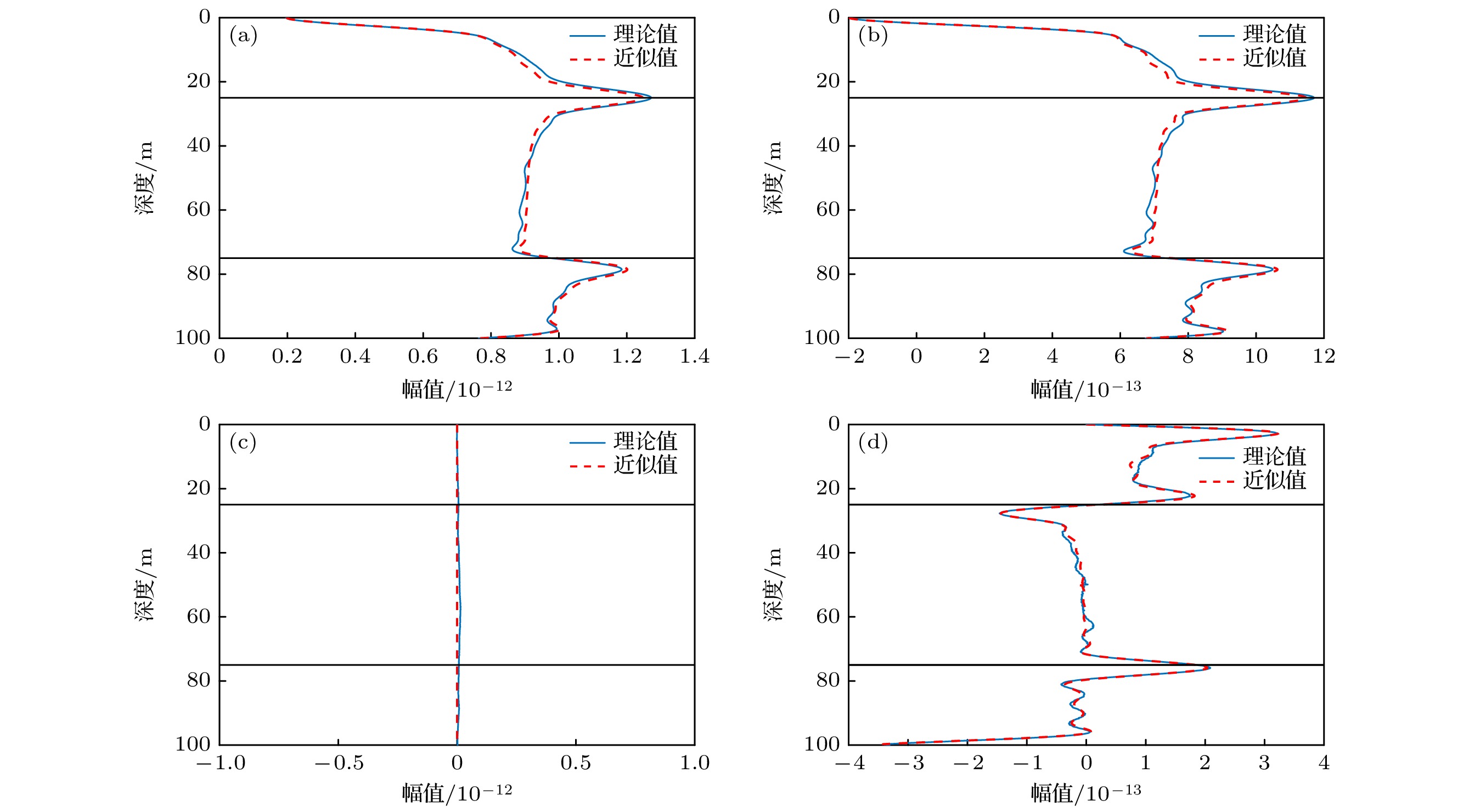
图 6 理想固体海底等声速波导环境下宽带Stokes参数深度分布曲线 (a) $S_0^{\left[ {{f_1}, {f_2}} \right]}$; (b) $S_1^{\left[ {{f_1}, {f_2}} \right]}$; (c) $S_2^{\left[ {{f_1}, {f_2}} \right]}$; (d) $S_3^{\left[ {{f_1}, {f_2}} \right]}$
Figure 6. Broadband Stokes parameters depth distribution curves for an ideal solid seabed isovelocity environment: (a) $S_0^{\left[ {{f_1}, {f_2}} \right]}$; (b) $S_1^{\left[ {{f_1}, {f_2}} \right]}$; (c) $S_2^{\left[ {{f_1}, {f_2}} \right]}$; (d) $S_3^{\left[ {{f_1}, {f_2}} \right]}$.
图 7 不同积分带宽条件下$S_0^{\left[ {{f_1}, {f_2}} \right]}$的误差值随距离的变化
Figure 7. Error value with range for different integration bandwidth.
图 8 非平稳相位近似成立距离${r_1}$与积分带宽的关系
Figure 8. Relationship between ${r_1}$ and integration bandwidth
图 9 Pekeris波导环境下宽带Stokes参数深度分布曲线 (a) $S_0^{\left[ {{f_1}, {f_2}} \right]}$; (b) $S_1^{\left[ {{f_1}, {f_2}} \right]}$; (c) $S_2^{\left[ {{f_1}, {f_2}} \right]}$; (d) $S_3^{\left[ {{f_1}, {f_2}} \right]}$
Figure 9. Broadband Stokes parameters depth distribution curves for Pekeris waveguide: (a) $S_0^{\left[ {{f_1}, {f_2}} \right]}$; (b) $S_1^{\left[ {{f_1}, {f_2}} \right]}$; (c) $S_2^{\left[ {{f_1}, {f_2}} \right]}$; (d) $S_3^{\left[ {{f_1}, {f_2}} \right]}$.
图 10 Pekeris波导环境下归一化宽带Stokes参数深度分布曲线 (a) 归一化宽带Stokes参数$s_1^{\left[ {{f_1}, {f_2}} \right]}$; (b) 归一化宽带Stokes参数$s_3^{\left[ {{f_1}, {f_2}} \right]}$
Figure 10. Normalized broadband Stokes parameters depth distribution curves for Pekeris waveguide: (a) Normalized broadband Stokes parameter $s_1^{\left[ {{f_1}, {f_2}} \right]}$; (b) normalized broadband Stokes parameter $s_3^{\left[ {{f_1}, {f_2}} \right]}$.
图 11 Pekeris波导环境下归一化宽带Stokes参数的深度-距离分布 (a) 归一化宽带Stokes参数$s_1^{\left[ {{f_1}, {f_2}} \right]}$; (b) 归一化宽带Stokes参数$s_3^{\left[ {{f_1}, {f_2}} \right]}$
Figure 11. Depth-range distribution of normalized broadband Stokes parameters for Pekeris waveguide: (a) Normalized broadband Stokes parameter $s_1^{\left[ {{f_1}, {f_2}} \right]}$; (b) normalized broadband Stokes parameter $s_3^{\left[ {{f_1}, {f_2}} \right]}$.
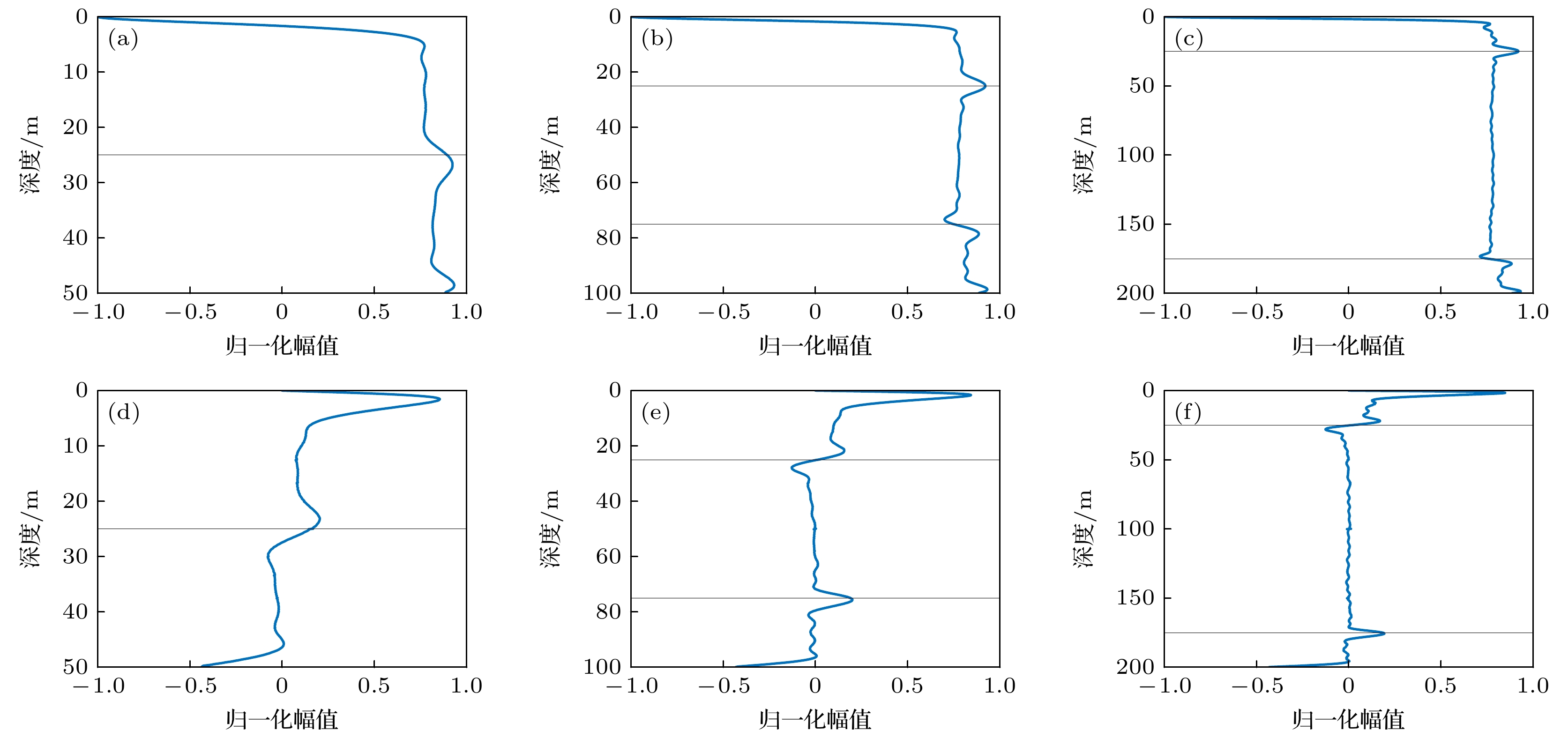
图 12 不同频率范围的归一化宽带Stokes参数深度分布曲线 (a) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(带宽$ {f_{{\text{c1}}}} $—125 Hz); (b) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(带宽$ {f_{{\text{c1}}}} $—250 Hz); (c) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(带宽$ {f_{{\text{c1}}}} $—500 Hz) ; (d) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(带宽$ {f_{{\text{c1}}}} $—125 Hz) ; (e) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(带宽$ {f_{{\text{c1}}}} $—250 Hz) ; (f) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(带宽$ {f_{{\text{c1}}}} $—500 Hz)
Figure 12. Normalized broadband Stokes parameters depth distribution curves for different frequency ranges: (a) $s_1^{\left[ {{f_1}, {f_2}} \right]}$($ {f_{{\text{c1}}}} $− 125 Hz); (b) $s_1^{\left[ {{f_1}, {f_2}} \right]}$($ {f_{{\text{c1}}}} $−250 Hz); (c) $s_1^{\left[ {{f_1}, {f_2}} \right]}$($ {f_{{\text{c1}}}} $－ 500 Hz); (d) $s_3^{\left[ {{f_1}, {f_2}} \right]}$($ {f_{{\text{c1}}}} $−125 Hz); (e) $s_3^{\left[ {{f_1}, {f_2}} \right]}$($ {f_{{\text{c1}}}} $−250 Hz); (f) $s_3^{\left[ {{f_1}, {f_2}} \right]}$($ {f_{{\text{c1}}}} $− 500 Hz)
图 13 不同声源深度的归一化宽带Stokes参数深度分布 (a) $s_1^{\left[ {{f_1}, {f_2}} \right]}$; (b) $s_3^{\left[ {{f_1}, {f_2}} \right]}$
Figure 13. Normalized broadband Stokes parameters depth distributions for different sound source depths: (a) $s_1^{\left[ {{f_1}, {f_2}} \right]}$; (b) $s_3^{\left[ {{f_1}, {f_2}} \right]}$.
图 14 声速剖面示意图
Figure 14. Sound speed profile.
图 15 不同声速剖面的归一化宽带Stokes参数深度分布曲线 (a) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(正梯度); (b) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(负梯度); (c) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(负跃层); (d) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(正梯度); (e) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(负梯度); (f) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(负跃层)
Figure 15. Normalized broadband Stokes parameters depth distribution curves for different sound speed profiles: (a) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(positive gradient); (b) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(negative gradient); (c) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(negative thermocline); (d) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(positive gradient); (e) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(negative gradient); (f) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(negative thermocline).
图 16 不同海深环境的归一化宽带Stokes参数深度分布曲线 (a) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(海深50 m); (b) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(海深100 m); (c) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(海深200 m); (d) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(海深50 m); (e) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(海深100 m); (f) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(海深200 m)
Figure 16. Normalized broadband Stokes parameters depth distribution curves for different depths of water column: (a) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(depth 50 m); (b) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(depth 100 m); (c) $s_1^{\left[ {{f_1}, {f_2}} \right]}$(depth 200 m); (d) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(depth 50 m); (e) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(depth 100 m); (f) $s_3^{\left[ {{f_1}, {f_2}} \right]}$(depth 200 m).
图 17 声压通道倒谱图
Figure 17. Cepstrogram of pressure channel.
图 18 目标方位估计结果
Figure 18. Results of ship azimuth estimation.
图 19 质点振速信号的时频图 (a) 水平质点振速${v_r}$; (b) 垂直质点振速${v_z}$
Figure 19. Spectrogram of the particle velocity: (a) horizontal particle velocity ${v_r}$; (b) vertical particle velocity ${v_z}$.
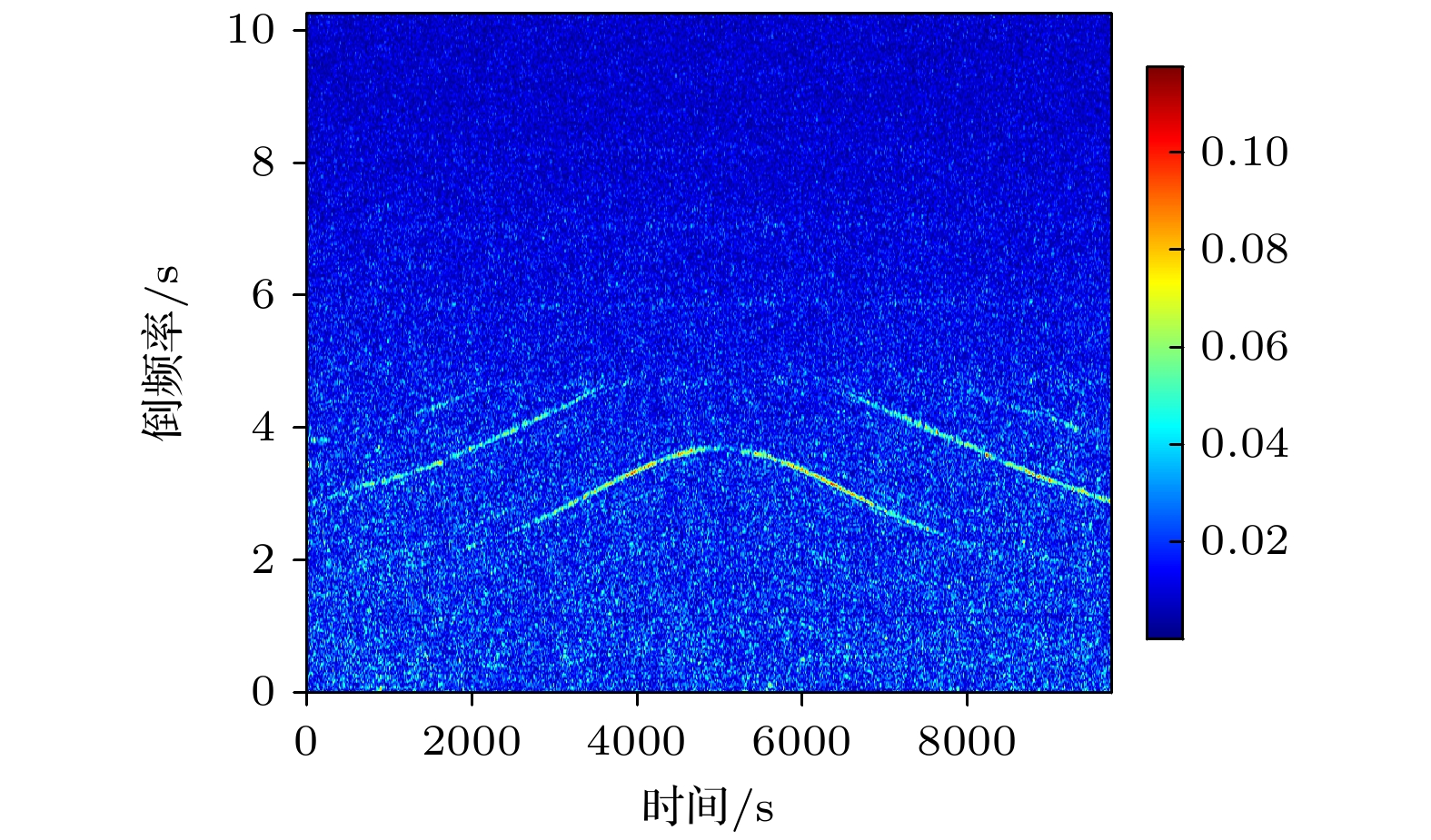
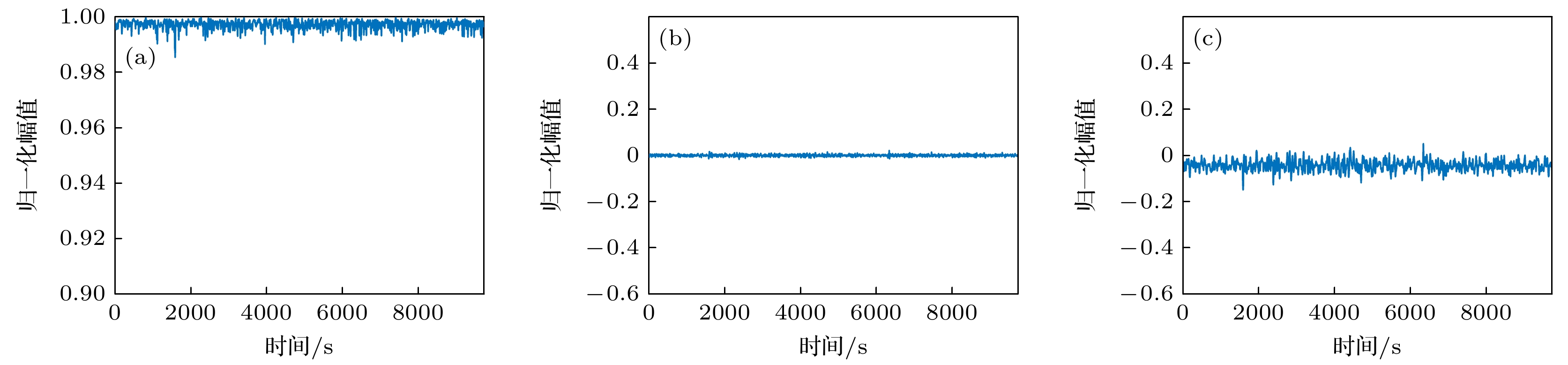
图 20 归一化宽带Stokes参数随时间的变化 (a) $s_1^{\left[ {{f_1}, {f_2}} \right]}$; (b) $s_2^{\left[ {{f_1}, {f_2}} \right]}$; (c) $s_3^{\left[ {{f_1}, {f_2}} \right]}$
Figure 20. Time-varying curves of the normalized broadband Stokes parameters: (a) $s_1^{\left[ {{f_1}, {f_2}} \right]}$; (b) $s_2^{\left[ {{f_1}, {f_2}} \right]}$; (c) $s_3^{\left[ {{f_1}, {f_2}} \right]}$.
-
[1] 休罗夫V 著 (贾志富 译) 2011 海洋矢量声学(北京: 国防工业出版社)第2—5页
Shchurov V (translated by Jia Z F) 2011 Vector Acoustics of the Ocean (Beijing: National Defense Industry Press) pp2–5
[2] 姜哲, 郭骅 1991 声学学报 16 330
Google Scholar
Jiang Z, Guo H 1991 Acta Acust. 16 330
Google Scholar
[3] Li J F, Pascal J C, Carles C 1998 J. Acoust. Soc. Am. 103 962
Google Scholar
[4] Shi C, Zhao R, Long Y, Yang S, Wang Y, Chen H, Ren J, Zhang X 2019 Natl. Sci. Rev. 6 707
Google Scholar
[5] Bliokh K Y, Nori F 2019 Phys. Rev. B 99 020301
Google Scholar
[6] Long Y, Ge H, Zhang D, Xu X, Ren J, Lu M H, Bao M, Chen H, Chen Y F 2020 Natl. Sci. Rev. 7 1024
Google Scholar
[7] Long Y, Zhang D, Yang C, Ge J, Chen H, Ren J 2020 Nat. Commun. 11 4716
Google Scholar
[8] Shchurov V A, Kuleshov V P, Cherkasov A V 2011 Acoust. Phys. 57 851
Google Scholar
[9] D’Spain G L, Hodgkiss W S 1991 J. Acoust. Soc. Am. 90 2300
Google Scholar
[10] Dall'Osto D R, Dahl P H 2013 J. Acoust. Soc. Am. 134 109
Google Scholar
[11] Dahl P H, Dall'Osto D R 2020 IEEE J. Oceanic Eng. 45 131
Google Scholar
[12] Dahl P H, Dall'Osto D R 2021 IEEE J. Oceanic Eng. 47 680
Google Scholar
[13] 刘伟 2014 博士学位论文 (哈尔滨: 哈尔滨工程大学)
Liu W 2014 Ph. D. Dissertation (Harbin: Harbin Engineering University
[14] Du B, Zhang W, Shi X 2016 IEEE/OES China Ocean Acoustics (COA) Harbin, China, August 8, 2016 pp1−3
[15] 韩雪 2020 博士学位论文 (哈尔滨: 哈尔滨工程大学)
Han X 2020 Ph. D. Dissertation (Harbin: Harbin Engineering University
[16] Bonnel J, Flamant J, Dall'Osto D R, Le Bihan N, Dahl P H 2021 J. Acoust. Soc. Am. 150 1897
Google Scholar
[17] 玻恩M, 沃尔夫 E 著 (杨葭荪 译) 2016 光学原理: 光的传播、干涉和衍射的电磁理论(北京: 电子工业出版社)第20—27页
Born M, Wolf E (translated by Yang J S) 2016 Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light (Beijing: Publishing House of Electronics Industry) pp20–27
[18] Dahl P H, Bonnel J 2022 J. Acoust. Soc. Am. 151 3818
Google Scholar
[19] Dahl P H, Dall'Osto D R, Hodgkiss W S 2023 J. Acoust. Soc. Am. 154 1482
Google Scholar
[20] Flamant J, Bonnel J 2023 J. Acoust. Soc. Am. 153 3012
Google Scholar
[21] 延森 F B, 库珀曼 W A, 波特 M B, 施米特 H 著 (周利生, 王鲁军, 杜栓平 译) 2017 计算海洋声学 (第2版) (北京: 国防工业出版社)第272—275页
Jensen F B, Kuperman W A, Porter M B, Schmidt H (translated by Zhou L S, Wang L J, Du S P) 2017 Computational Ocean Acoustics (2nd Ed.) (Beijing: National Defense Industry Press) pp272–275
[22] Tsekhmistrenko M, Sigloch K, Hosseini K, Barruol G 2021 Nat. Geosci. 14 612
Google Scholar
[23] Trabattoni A, Barruol G, Dréo R, Boudraa A 2023 J. Acoust. Soc. Am. 153 260
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2227
- PDF Downloads: 67
- Cited By: 0
