-
Since the Whitham modulation theory was first proposed in 1965, it has been widely concerned because of its superiority in studying dispersive fluid dynamics and dealing with discontinuous initial value problems. In this paper, the Whitham modulation theory of the defocusing nonlinear Schrödinger equation is developed, and the classification and evolution of the solutions of discontinuous initial value problem are studied. Moreover, the dispersive shock wave region, the rarefaction wave region, the unmodulated wave region and the plateau region are distinguished. Particularly, the correctness of the results is verified by direct numerical simulation. Specifically, the solutions of 0-phase and 1-phase and their corresponding Whitham equations are derived by the finite gap integration method. Also the Whitham equation of genus N corresponding to the N-phase periodic wave solution is derived. The basic structures of rarefaction wave and dispersive shock wave are given, in which the boundaries of the regions are calculated in detail. The Riemann invariants and density distributions of dispersive fluids in each case are discussed. When the initial value is fixed as a special one, the vacuum point is considered and analyzed in detail. In addition, the oscillating front and the soliton front in the dispersive shock wave are considered. In fact, the Whitham modulation theory has many wonderful applications in real physics and engineering. The dam problem is investigated as a special Riemann problem, the piston problem of dispersive fluid is analyzed, and the novel undular bores are found.
-
Keywords:
- Whitham modulation theory /
- Lax pair /
- Riemann problem /
- rarefaction wave /
- dispersive shock wave
[1] Whitham G B 1965 J. Fluid Mech. 22 273
Google Scholar
[2] Luke J C 1966 Proc. R. Soc. London, Ser. A 292 403
[3] Flaschka H, Forest M G, McLaughlin D W 1980 Commun. Pure Appl. Math. 33 739
Google Scholar
[4] Hoefer M A, Ablowitz M J, Coddington I, Cornell E A, Engels P, Schweikhard V 2006 Phys. Rev. A 74 023623
Google Scholar
[5] Mo Y C, Kishek R A, Feldman D, Haber I, Beaudoin B, O’Shea P G, Thangaraj J C T 2013 Phys. Rev. Lett. 110 084802
Google Scholar
[6] Trillo S, Deng G, Biondini G, Klein M, Clauss G F, Chabchoub A, Onorato M 2016 Phys. Rev. Lett. 117 144102
Google Scholar
[7] Maiden M D, Lowman N K, Anderson D V, Schubert M E, Hoefer M A 2016 Phys. Rev. Lett. 116 174501
Google Scholar
[8] Xu G, Conforti M, Kudlinski A, Mussot A 2017 Phys. Rev. Lett. 118 254101
Google Scholar
[9] Wan W, Jia S, Fleischer J W 2007 Nat. Phys. 3 46
Google Scholar
[10] Conti C, Fratalocchi A, Peccianti M, Ruocco G, Trillo S 2009 Phys. Rev. Lett. 102 083902
Google Scholar
[11] Fatome J, Finot C, Millot G, Armaroli A, Trillo S 2014 Phys. Rev. X 4 021022
[12] Wang J, Li J, Lu D, Guo Q, Hu W 2015 Phys. Rev. A 91 063819
Google Scholar
[13] Xu G, Mussot A, Kudlinski A, Trillo S, Copie F, Conforti M 2016 Opt. Lett. 41 2656
Google Scholar
[14] Millot G, Pitois S, Yan M, Hovhannisyan T, Bendahmane A, Hänsch T W, Picqué N 2016 Nat. Photonics 10 27
Google Scholar
[15] Bendahmane A, Xu G, Conforti M, Kudlinski A, Mussot A, Trillo S 2022 Nat. Commun. 13 3137
Google Scholar
[16] Jenkins R 2015 Nonlinearity 28 2131
Google Scholar
[17] Zhang X F, Wen L, Wang L X, Chen G P, Tan R B, Saito H 2022 Phys. Rev. A 105 033306
Google Scholar
[18] Bilman D, Buckingham R, Wang D S 2021 J. Diff. Equ. 297 320
Google Scholar
[19] Lou S Y, Hao X 2022 Phys. Lett. A 443 128203
Google Scholar
[20] Zhao L C, Xin G G, Yang Z Y, Yang W L 2022 Phys. D 435 133283
Google Scholar
[21] Wang D S, Xu L, Xuan Z 2022 J. Nonlinear Sci. 32 3
Google Scholar
[22] Liu Y, Wang D S 2022 Stud. Appl. Math. 149 588
Google Scholar
[23] Abeya A, Biondini G, Hoefer M A 2023 J. Phys. A: Math. Theor. 56 025701
Google Scholar
[24] Saleh B, Smyth N F 2023 Proc. R. Soc. A 479 20220580
Google Scholar
[25] Gong R, Wang D S 2022 Appl. Math. Lett. 126 107795
Google Scholar
[26] Gong R, Wang D S 2022 Phys. D 439 133398
Google Scholar
[27] El G A, Geogjaev V V, Gurevich A V, Krylov A L 1995 Phys. D 87 186
Google Scholar
[28] Congy T, El G A, Hoefer M A, Shearer M 2019 Stud. Appl. Math. 142 241
Google Scholar
[29] Dressler R F 1954 Assemblé Général de Rome 38 319
[30] Dressler R F 1952 J. Res. Nat. Bur. Stand. 49 2356
[31] Congy T, Ivanov S K, Kamchatnov A M, Pavloff N 2017 Chaos 27 083107
Google Scholar
-
图 1 两种类型的稀疏波结构 (a)
$\lambda_{2}$ 为常数; (b)$\lambda_{1}$ 为常数Figure 1. Two types of RW structure: (a)
$\lambda_{2}$ is constant; (b)$\lambda_{1}$ is constant
图 2 两种冲击波结构及其对应的色散冲击波
Figure 2. Two types of DSW structure and their corresponding dispersive shock waves
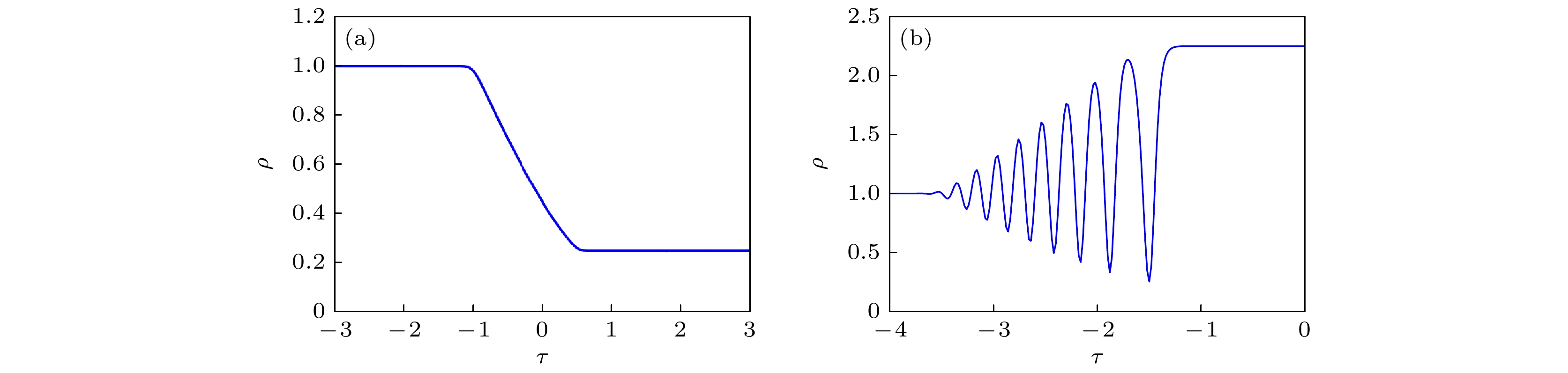
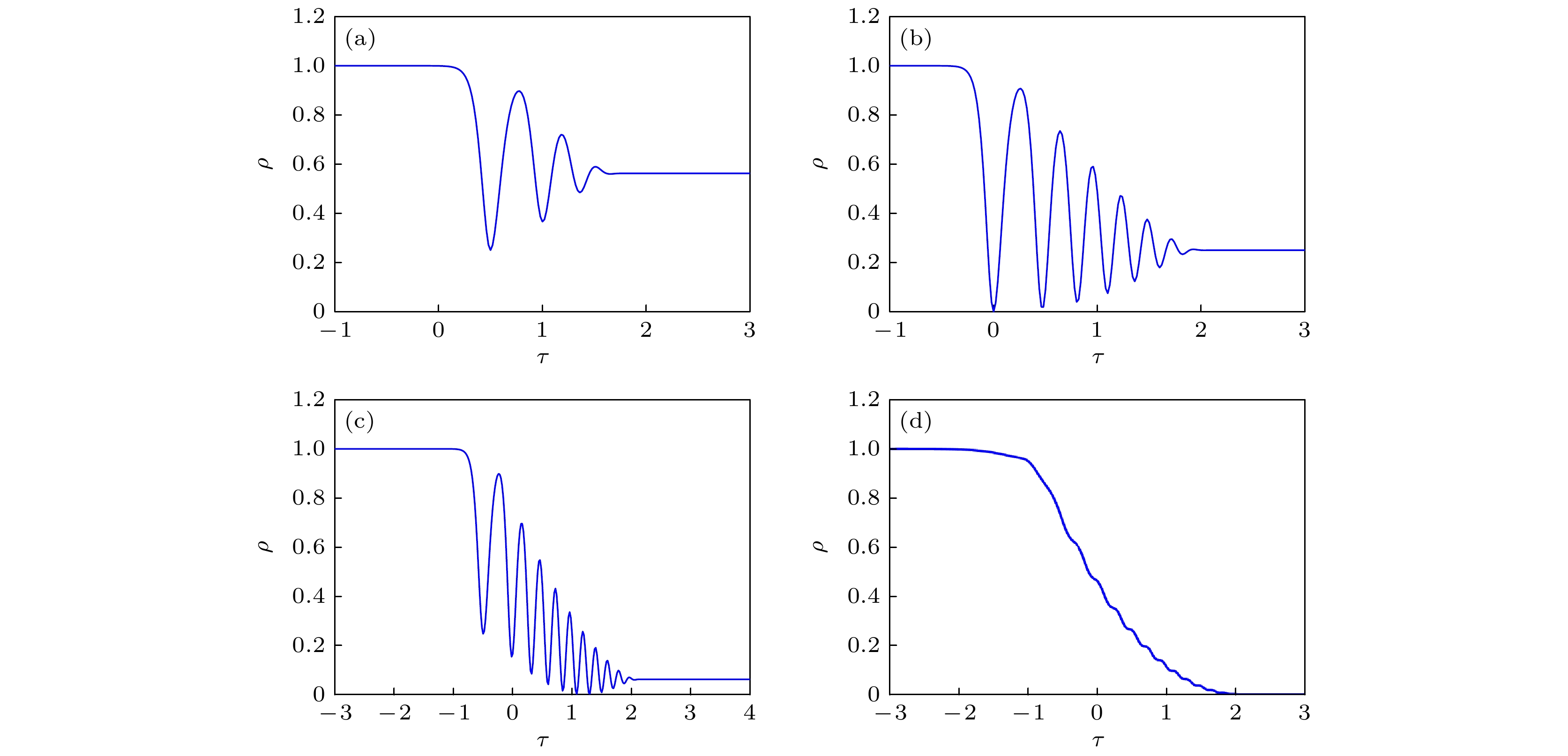
图 4 方程(1)在特殊初值问题(83)式和(84)式下的演化情形 (a)
$\rho=9/16,\; v=-0.5,\; d=-0.5$ ; (b)$\rho=1/4, \;v=-1,\; d=0$ ; (c)$\rho= 1/16, \;v=-1.5,\; d=0.5$ ; (d)$\rho=0.0001, \;v=-1.98,\; d=0.98$ Figure 4. Evolution of the Eq. (1) under special initial value problems Eq. (83) and Eq. (84): (a)
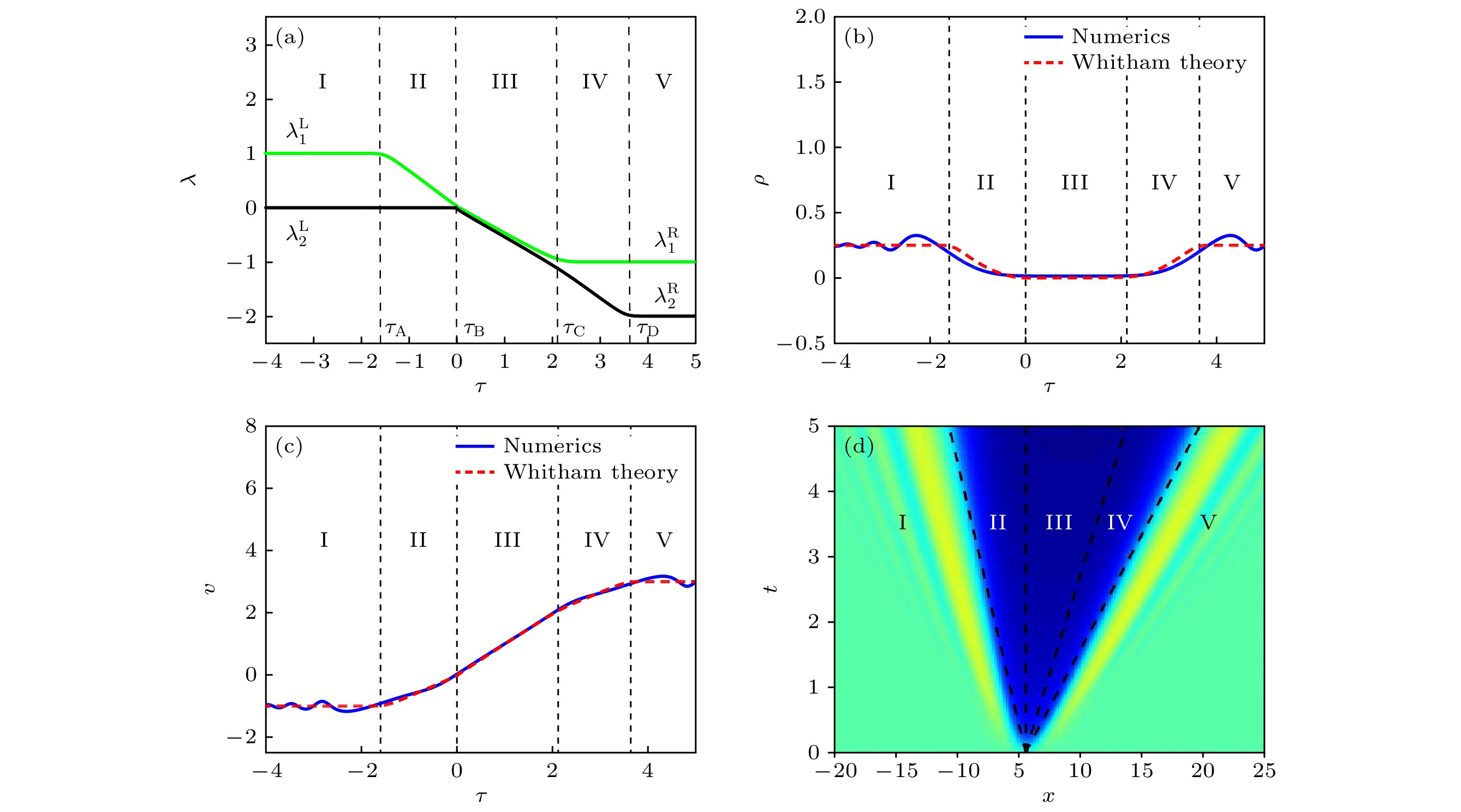
$\rho=9/ 16, \;v=-0.5, \;d=-0.5$ ; (b)$\rho= $ $ 1/4, \;v=-1, \;d=0$ ; (c)$\rho=1/16,\; v=-1.5, \;d=0.5$ ; (d)$\rho=0.0001, \;v=-1.98,\; d=0.98$ 
图 6 情况A下(a)黎曼不变量的分布、(b)密度函数ρ的波形结构、(c)速度函数v的波形结构与(d)密度函数ρ的演化过程. 其中, 参数选择为
$t=5,\ \lambda_2^{{\rm{L}}}=0,\ \lambda_1^{{\rm{L}}}=1, \ \lambda_2^{{\rm{R}}}=-2,\ \lambda_1^{{\rm{R}}}=-1$ Figure 6. (a) Distribution of Riemann invariants, (b) the waveform structure of density function ρ, (c) the waveform structure of velocity function v and (d) the evolution process of density function ρ for Case A. The parameters are
$t=5,\ \lambda_2^{{\rm{L}}}=0,\ \lambda_1^{{\rm{L}}}= 1, $ $ \ \lambda_2^{{\rm{R}}}=-2,\ \lambda_1^{{\rm{R}}}=-1$ 
图 7 情况A—情况E在
$(v, \rho)$ 平面中解的行为Figure 7. Behavior of the solution in the
$(v, \rho)$ plane for Case A–Case E
图 8 情况B下(a)黎曼不变量的分布、(b)密度函数ρ的波形结构、(c)速度函数v的波形结构与(d)密度函数ρ的演化过程. 其中, 参数选择为
$t=5, \;\lambda_2^{{\rm{L}}}=-1,\; \lambda_1^{{\rm{L}}}=1,\; \lambda_2^{{\rm{R}}}=-2,\; \lambda_1^{{\rm{R}}}=0$ Figure 8. (a) Distribution of Riemann invariants, (b) the waveform structure of density function ρ, (c) the waveform structure of velocity function v and (d) the evolution process of density function ρ for Case B. The parameters are
$t=5, \;\lambda_2^{{\rm{L}}}=-1, $ $ \;\lambda_1^{{\rm{L}}}=1,\; \lambda_2^{{\rm{R}}}=-2,\; \lambda_1^{{\rm{R}}}=0$ 
图 9 情况C下(a)黎曼不变量的分布、(b)密度函数ρ的波形结构、(c)速度函数v的波形结构与(d)密度函数ρ的演化过程. 其中, 参数选择为
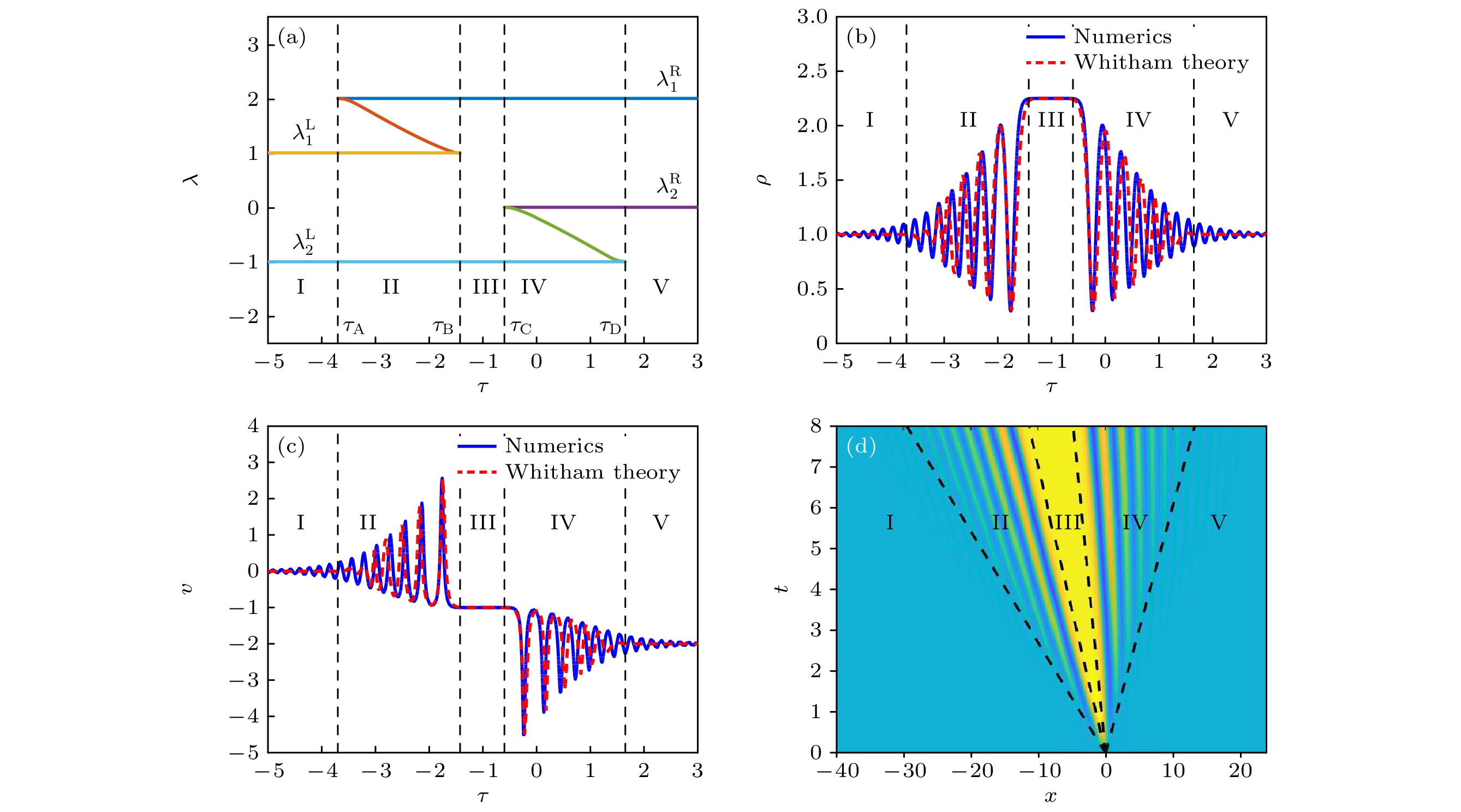
$t=8,\; \lambda_2^{{\rm{L}}}=-1,\; \lambda_1^{{\rm{L}}}=0, \;\lambda_2^{{\rm{R}}}=-2,\; \lambda_1^{{\rm{R}}}=2$ Figure 9. (a) Distribution of Riemann invariants, (b) the waveform structure of density function ρ, (c) the waveform structure of velocity function v and (d) the evolution process of density function ρ for Case C. The parameters are
$t=8, \;\lambda_2^{{\rm{L}}}=-1,\; $ $ \lambda_1^{{\rm{L}}}=0,\; \lambda_2^{{\rm{R}}}=-2,\; \lambda_1^{{\rm{R}}}=2$ 
图 10 情况D下(a)黎曼不变量的分布、(b)密度函数ρ的波形结构、(c)速度函数v的波形结构与(d)密度函数ρ的演化过程. 其中, 参数选择为
$t=5,\; \lambda_2^{{\rm{L}}}=-2, \;\lambda_1^{{\rm{L}}}=1,\; \lambda_2^{{\rm{R}}}=-1,\; \lambda_1^{{\rm{R}}}=0$ Figure 10. (a) Distribution of Riemann invariants, (b) the waveform structure of density function ρ, (c) the waveform structure of velocity function v and (d) the evolution process of density function ρ for Case D. The parameters are
$t=5,\; \lambda_2^{{\rm{L}}}=-2, $ $ \;\lambda_1^{{\rm{L}}}=1,\; \lambda_2^{{\rm{R}}}=-1,\; \lambda_1^{{\rm{R}}}=0$ 
图 11 情况A大坝问题的(a)黎曼不变量与(b)密度函数的分布图. 其中时间为
$t=5$ Figure 11. (a) Distribution of Riemann invariants and (b) density function for the dam problem for Case A, where
$t=5$ 
图 12 情况D大坝问题的(a)黎曼不变量与(b)密度函数的分布图. 其中时间为
$t=5$ Figure 12. (a) Distribution of Riemann invariants and (b) density function for the dam problem for Case D, where
$t=5$ 
图 13 情况E下(a)黎曼不变量的分布、(b)密度函数ρ的波形结构、(c)速度函数v的波形结构与(d)密度函数ρ的演化过程. 其中, 参数选择为
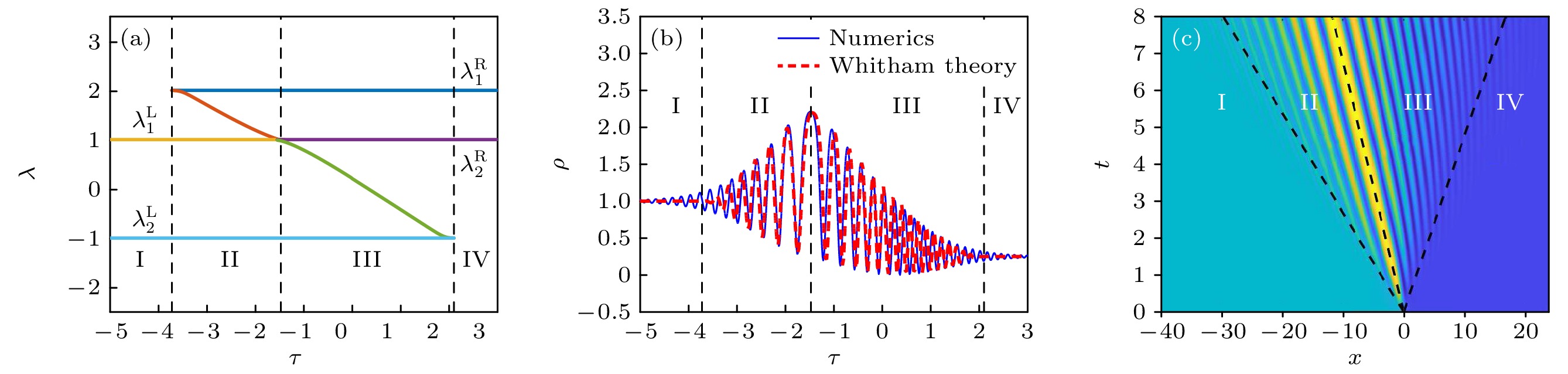
$t=8,\; \lambda_2^{{\rm{L}}}=-1, \;\lambda_1^{{\rm{L}}}=1,\; \lambda_2^{{\rm{R}}}=0,\; \lambda_1^{{\rm{R}}}=2$ Figure 13. (a) Distribution of Riemann invariants, (b) the waveform structure of density function ρ, (c) the waveform structure of velocity function v and (d) the evolution process of density function ρ for Case E. The parameters are
$t=8,\;\lambda_2^{{\rm{L}}}=-1, $ $ \;\lambda_1^{{\rm{L}}}=1, \;\lambda_2^{{\rm{R}}}=0,\; \lambda_1^{{\rm{R}}}=2$ 
图 14 情况E的特殊情形下, (a)黎曼不变量的分布、(b)密度函数ρ的波形结构和(c)密度函数ρ分量的演化过程. 其中, 参数选择为
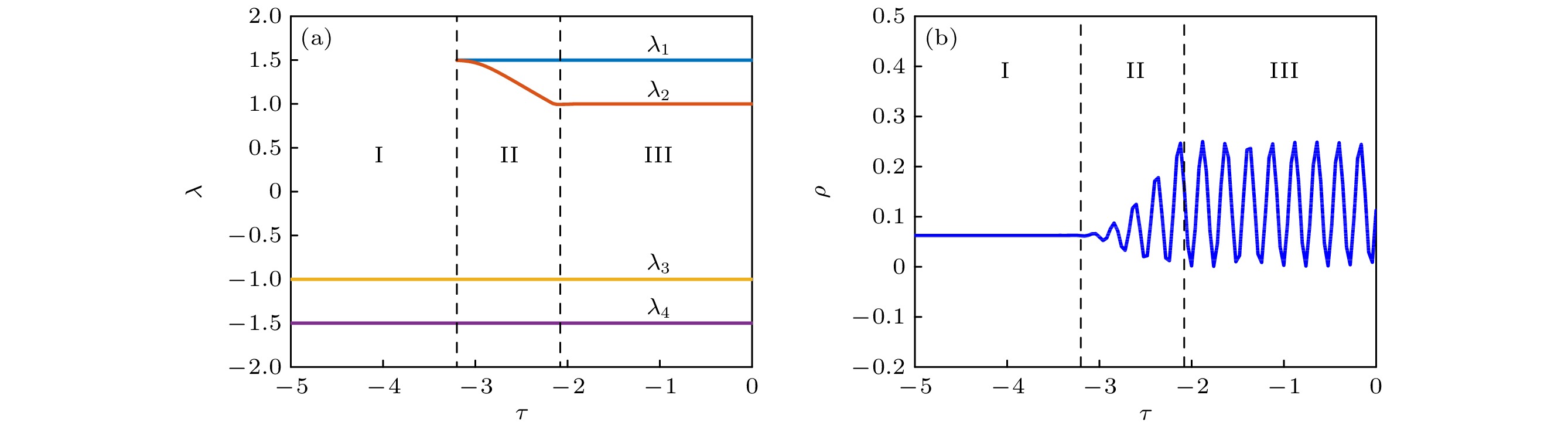
$t=8,\; \lambda_2^{{\rm{L}}}=-1,\; \lambda_1^{{\rm{L}}}=\lambda_2^{{\rm{R}}}=1,\; \lambda_1^{{\rm{R}}}=$ 2Figure 14. (a) Distribution of Riemann invariants, (b) the waveform structure of density function ρ and (c) the evolution process of density function ρ for the special case of Case E. The parameters are
$t=8,\; \lambda_2^{{\rm{L}}}=-1,\; \lambda_1^{{\rm{L}}}=\lambda_2^{{\rm{R}}}=1,\; \lambda_1^{{\rm{R}}}=2$ 
图 15 情况F中(a)黎曼不变量的分布、(b)密度函数ρ的波形结构和(c)密度函数ρ的演化过程. 其中, 参数选择为
$t=8,\; $ $ \lambda_2^{{\rm{L}}}=-1, \;\lambda_1^{{\rm{L}}}=0,\; \lambda_2^{{\rm{R}}}=1,\; \lambda_1^{{\rm{R}}}=2$ Figure 15. (a) Distribution of Riemann invariants, (b) the waveform structure of density function ρ and (c) the evolution process of density function ρ for Case F. The parameters are
$t=8, \;\lambda_2^{{\rm{L}}}=-1,\; \lambda_1^{{\rm{L}}}=0,\; \lambda_2^{{\rm{R}}}=1,\; \lambda_1^{{\rm{R}}}=2$ 
图 16 活塞问题中, (a)黎曼不变量的分布与(b)密度函数ρ的波形结构, 其中时间选取为
$t=5$ Figure 16. (a) Distribution of the Riemann invariant and (b) the waveform structure of the density function ρ in the piston problem, where
$t=5$ -
[1] Whitham G B 1965 J. Fluid Mech. 22 273
Google Scholar
[2] Luke J C 1966 Proc. R. Soc. London, Ser. A 292 403
[3] Flaschka H, Forest M G, McLaughlin D W 1980 Commun. Pure Appl. Math. 33 739
Google Scholar
[4] Hoefer M A, Ablowitz M J, Coddington I, Cornell E A, Engels P, Schweikhard V 2006 Phys. Rev. A 74 023623
Google Scholar
[5] Mo Y C, Kishek R A, Feldman D, Haber I, Beaudoin B, O’Shea P G, Thangaraj J C T 2013 Phys. Rev. Lett. 110 084802
Google Scholar
[6] Trillo S, Deng G, Biondini G, Klein M, Clauss G F, Chabchoub A, Onorato M 2016 Phys. Rev. Lett. 117 144102
Google Scholar
[7] Maiden M D, Lowman N K, Anderson D V, Schubert M E, Hoefer M A 2016 Phys. Rev. Lett. 116 174501
Google Scholar
[8] Xu G, Conforti M, Kudlinski A, Mussot A 2017 Phys. Rev. Lett. 118 254101
Google Scholar
[9] Wan W, Jia S, Fleischer J W 2007 Nat. Phys. 3 46
Google Scholar
[10] Conti C, Fratalocchi A, Peccianti M, Ruocco G, Trillo S 2009 Phys. Rev. Lett. 102 083902
Google Scholar
[11] Fatome J, Finot C, Millot G, Armaroli A, Trillo S 2014 Phys. Rev. X 4 021022
[12] Wang J, Li J, Lu D, Guo Q, Hu W 2015 Phys. Rev. A 91 063819
Google Scholar
[13] Xu G, Mussot A, Kudlinski A, Trillo S, Copie F, Conforti M 2016 Opt. Lett. 41 2656
Google Scholar
[14] Millot G, Pitois S, Yan M, Hovhannisyan T, Bendahmane A, Hänsch T W, Picqué N 2016 Nat. Photonics 10 27
Google Scholar
[15] Bendahmane A, Xu G, Conforti M, Kudlinski A, Mussot A, Trillo S 2022 Nat. Commun. 13 3137
Google Scholar
[16] Jenkins R 2015 Nonlinearity 28 2131
Google Scholar
[17] Zhang X F, Wen L, Wang L X, Chen G P, Tan R B, Saito H 2022 Phys. Rev. A 105 033306
Google Scholar
[18] Bilman D, Buckingham R, Wang D S 2021 J. Diff. Equ. 297 320
Google Scholar
[19] Lou S Y, Hao X 2022 Phys. Lett. A 443 128203
Google Scholar
[20] Zhao L C, Xin G G, Yang Z Y, Yang W L 2022 Phys. D 435 133283
Google Scholar
[21] Wang D S, Xu L, Xuan Z 2022 J. Nonlinear Sci. 32 3
Google Scholar
[22] Liu Y, Wang D S 2022 Stud. Appl. Math. 149 588
Google Scholar
[23] Abeya A, Biondini G, Hoefer M A 2023 J. Phys. A: Math. Theor. 56 025701
Google Scholar
[24] Saleh B, Smyth N F 2023 Proc. R. Soc. A 479 20220580
Google Scholar
[25] Gong R, Wang D S 2022 Appl. Math. Lett. 126 107795
Google Scholar
[26] Gong R, Wang D S 2022 Phys. D 439 133398
Google Scholar
[27] El G A, Geogjaev V V, Gurevich A V, Krylov A L 1995 Phys. D 87 186
Google Scholar
[28] Congy T, El G A, Hoefer M A, Shearer M 2019 Stud. Appl. Math. 142 241
Google Scholar
[29] Dressler R F 1954 Assemblé Général de Rome 38 319
[30] Dressler R F 1952 J. Res. Nat. Bur. Stand. 49 2356
[31] Congy T, Ivanov S K, Kamchatnov A M, Pavloff N 2017 Chaos 27 083107
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4025
- PDF Downloads: 158
- Cited By: 0
