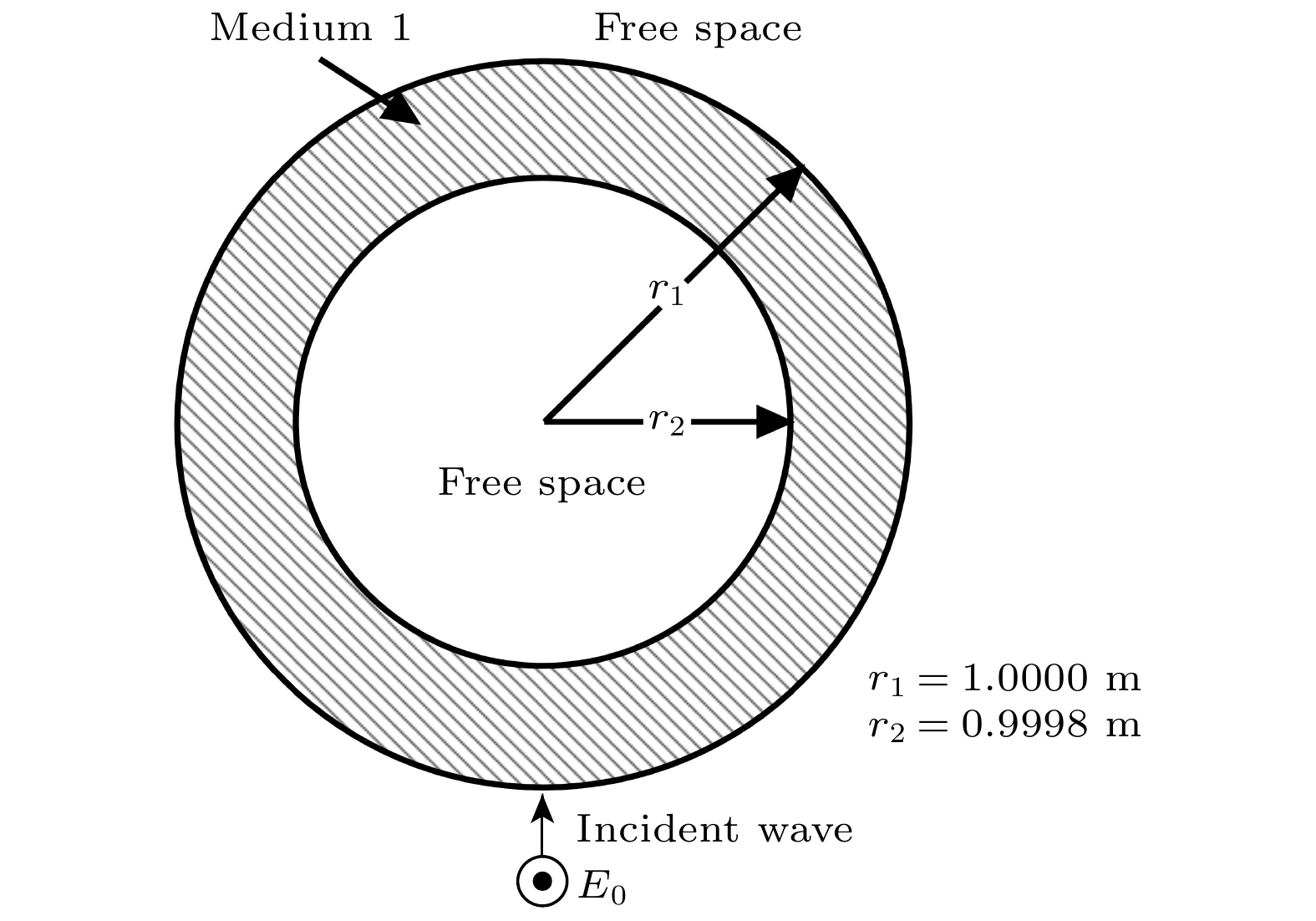
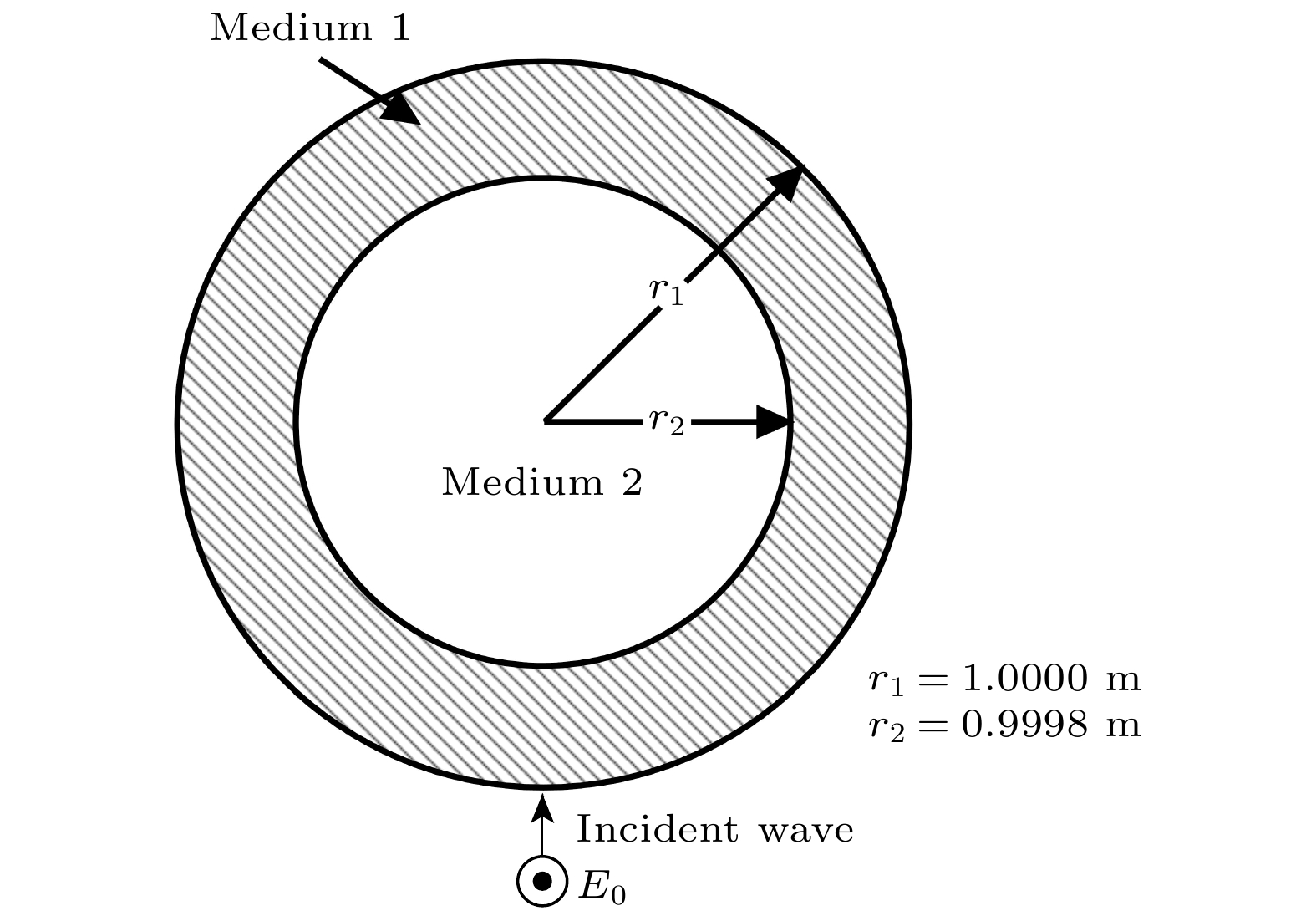
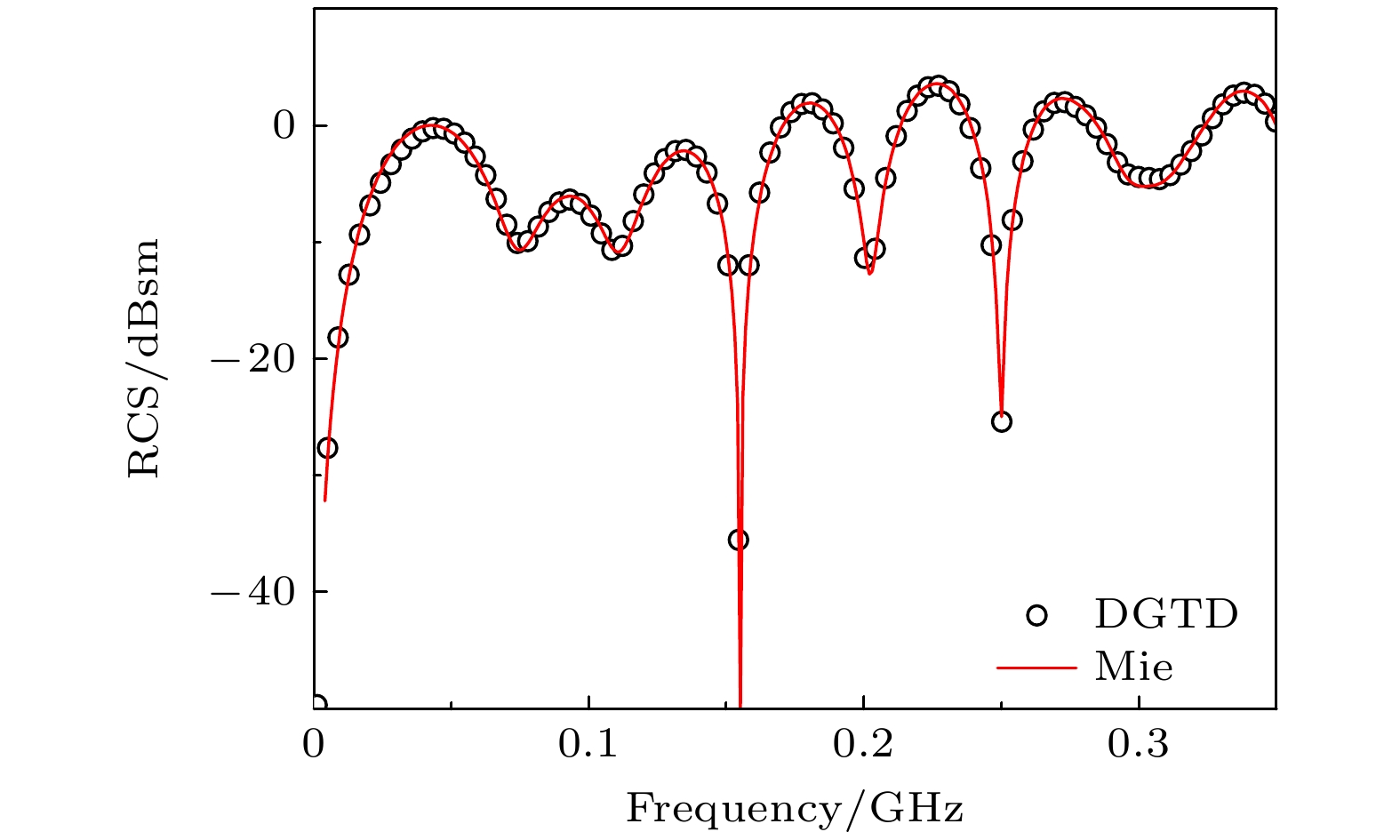
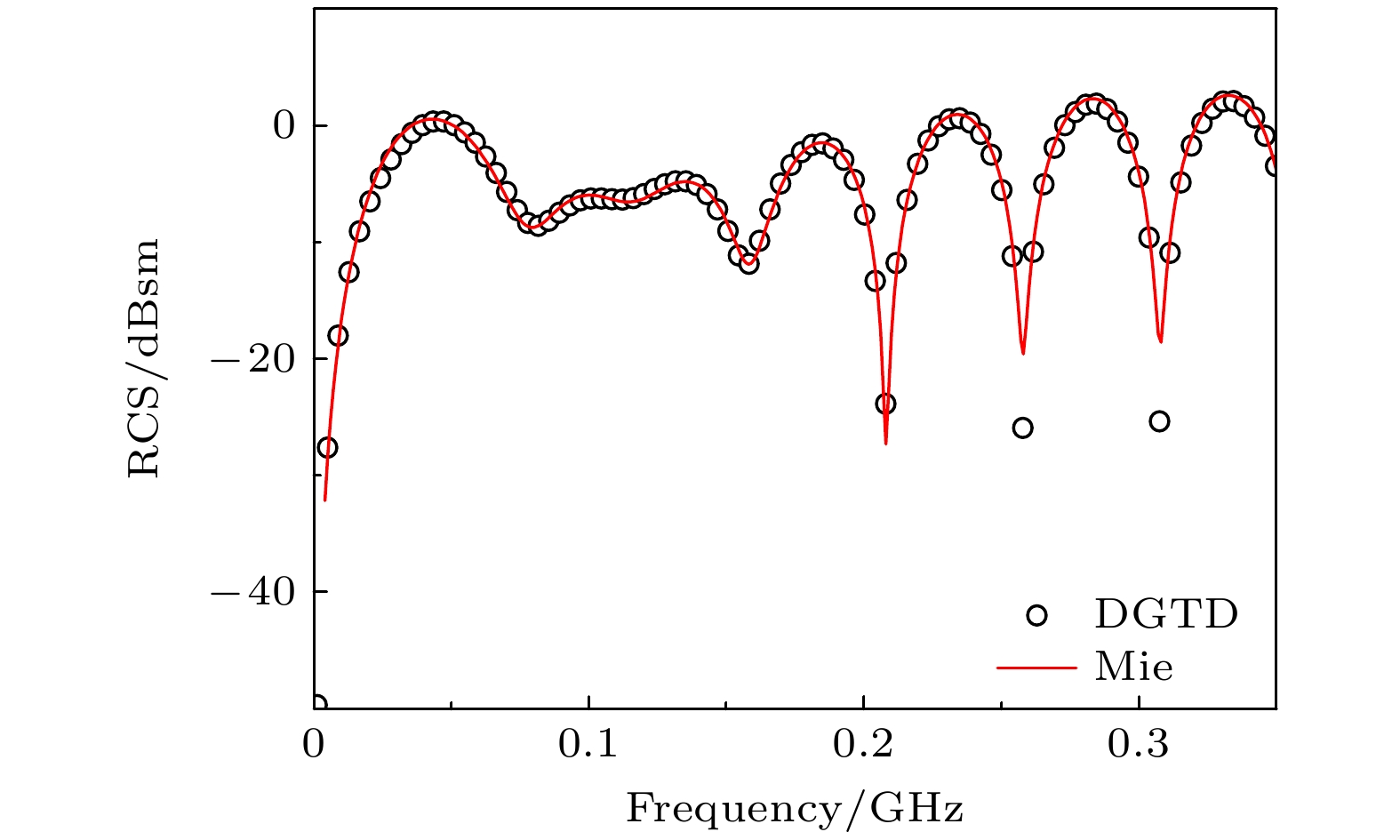
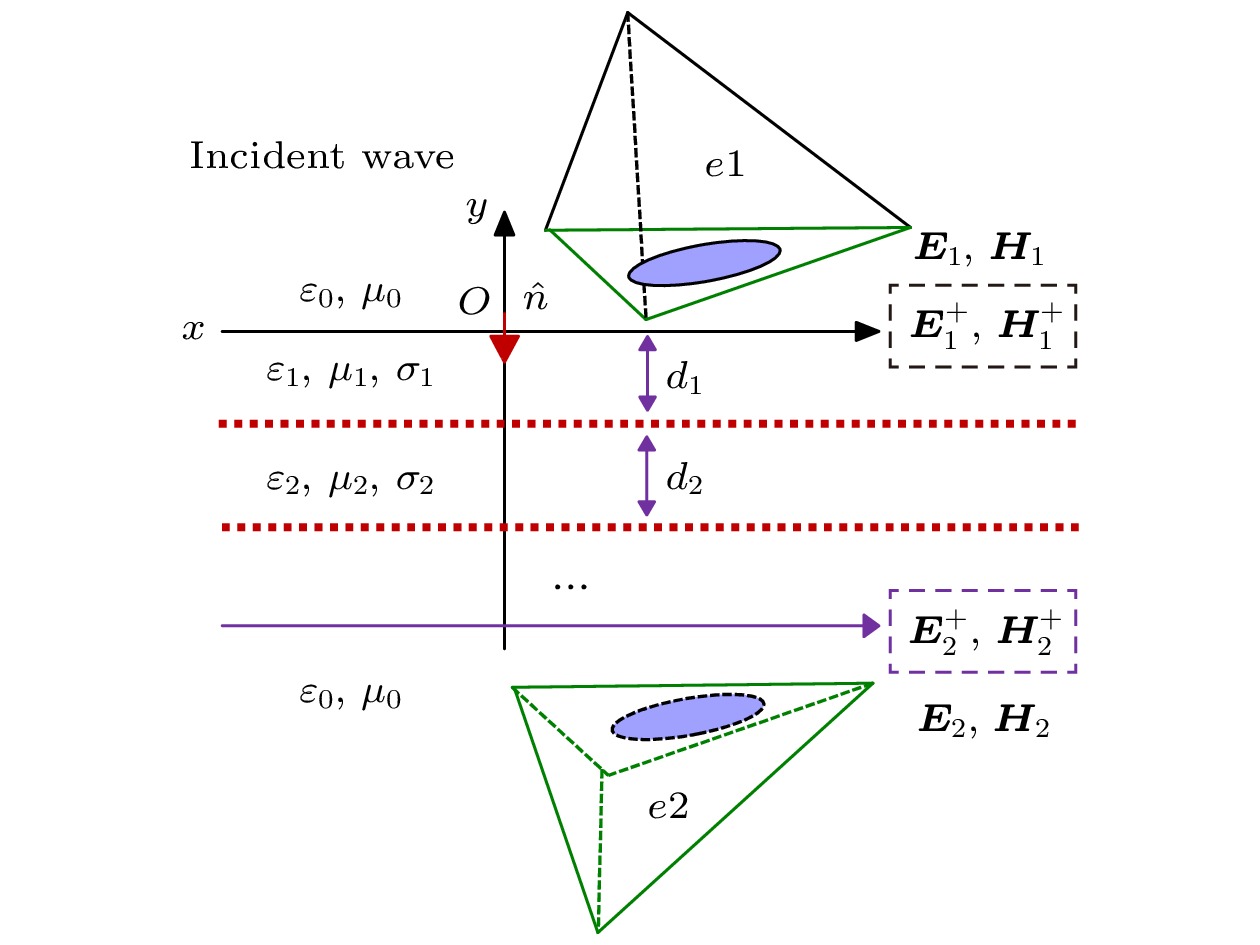
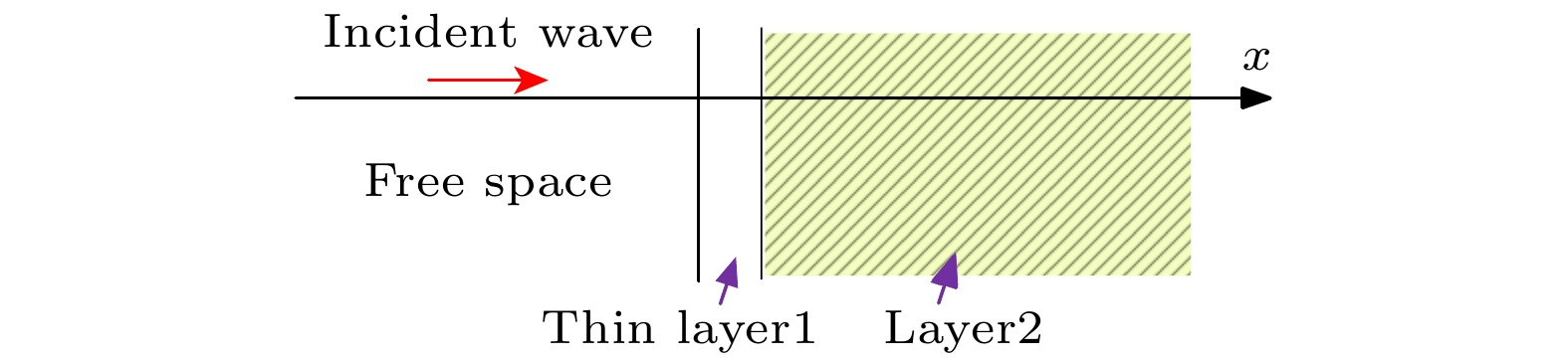
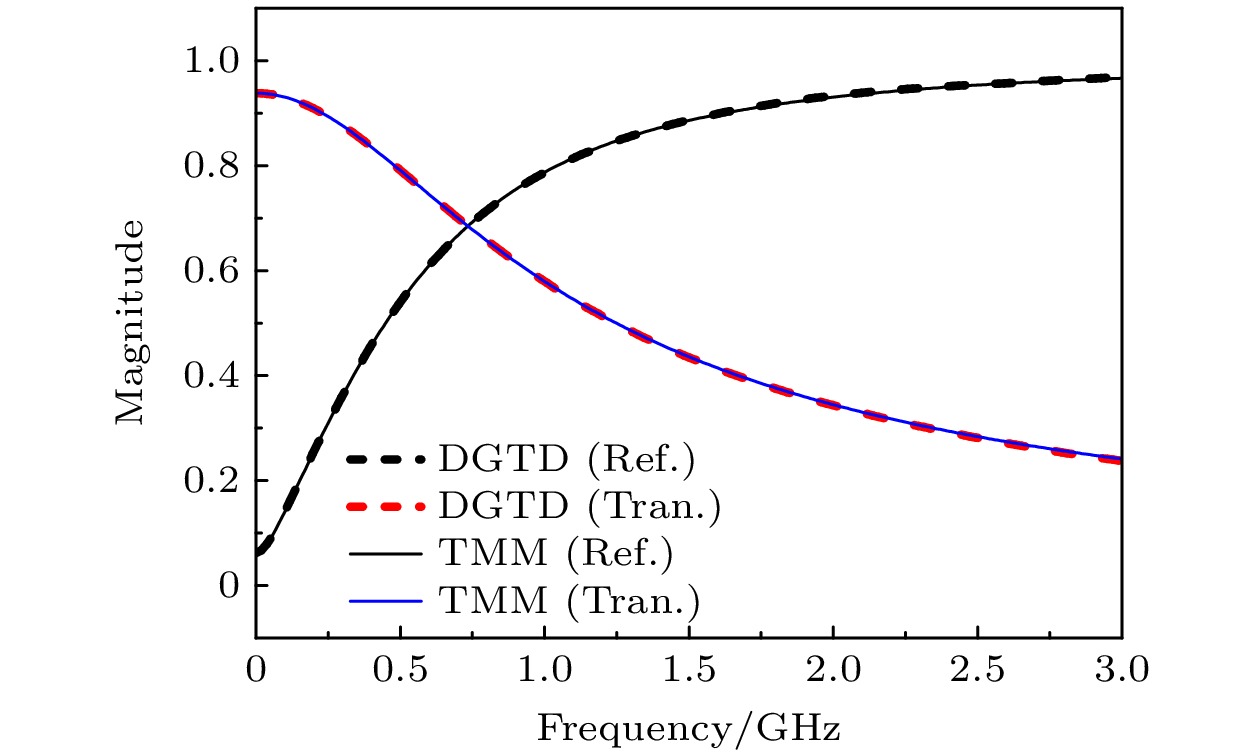
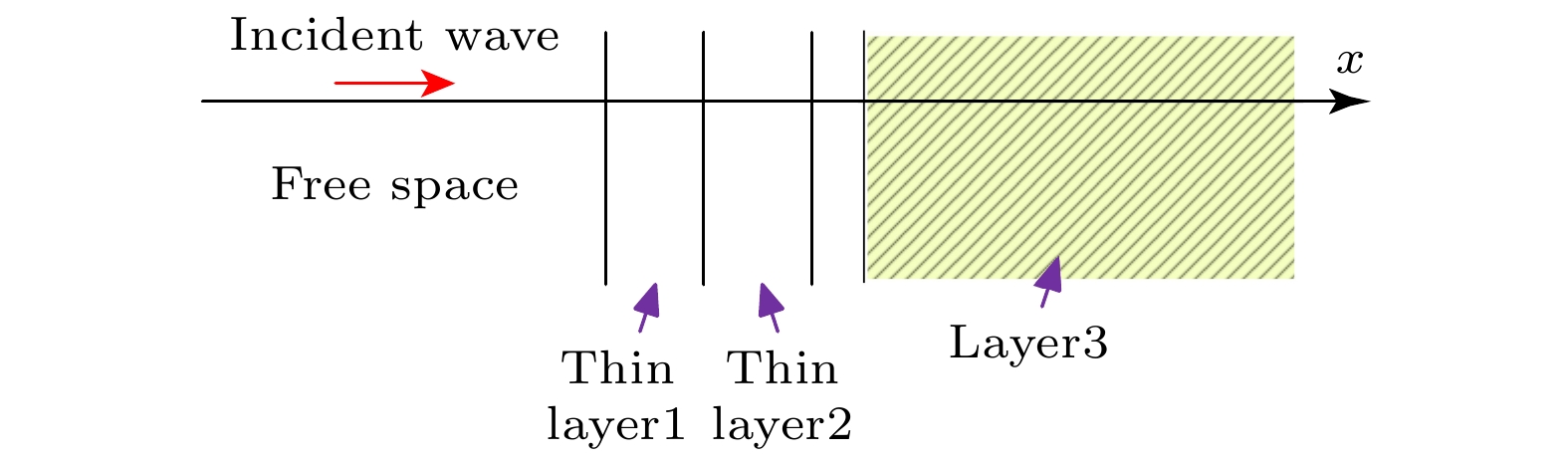
-
The thin layer problem is common in some engineering cases, such as a coating target or dielectric radome. If the skin depth of the medium behind the thin layer is much smaller than the medium scale, the transmission line impedance boundary can be used to solve the thin layer problem . When both sides of the thin layer are free space or the skin depth of the medium behind the thin layer is greater than or comparable to the scale of the medium, the transmission line impedance boundary condition is not applicable. Such problems need incident and reflected wave data and are also known as penetrable thin-layer problems. When dealing with penetrable thin-layer problems, we need to give the electromagnetic wave data on both sides. In addition, the thin layer problem can belong with multi-scale problems. The EM simulation is difficult to implement because of the high resource consumption of accurate modeling. The accurate modeling is a very expensive algorithm, and the mesh-size difference between the thin layer region and the surrounding ordinary region is too large, thus seriously affecting the quality of the elements (tetrahedrons). So, it is difficult to solve the problem of thin layer quickly by using the time-domain discontinuous Galerkin method or even by using local time steps or other optimization methods. To acquire a fast solution, the approximate boundary condition can be used to describe the thin layer. The DGTD has also the advantage of the geometric fitting property. If a thin layer model is curved, we can build a conformal geometric model to deal with the thin layer, thus avoiding the complicated interpolation correction scheme. In this work, A robust DGTD method for penetrable thin layers is proposed. In our study, we find that the current excitation scheme is prone to divergence when large dielectric coefficients are dealt with and its robustness is poor. To solve this problem, we use the electromagnetic field correction scheme in DGTD to deal with the thin layer problems. In addition, engineering problems may encounter multiple thin layers. In this work, a simulation scheme for multiple thin layers is presented and relevant numerical examples are given to verify it. The results illustrate the accuracy and effectiveness of the method in this work, and the method presented in this work can be used for the fast calculation of complex thin layer problems. [1] Feliziani M 2011 IEEE Trans. Electromagn. Compat. 54 299
Google Scholar
[2] Hanson G W 2008 J. Appl. Phys. 103 064302
Google Scholar
[3] Shapoval O V, Gomez-Diaz J S, Perruisseau-Carrier J, Mosig J R, Nosich A I 2013 IEEE Trans. Terahertz Sci. Technol. 3 666
Google Scholar
[4] Maloney J G, Smith G S 1992 IEEE Trans. Antennas Propag. 40 323
Google Scholar
[5] Richmond J 1965 IEEE Trans. Antennas Propag. 13 334
Google Scholar
[6] Harrington R, Mautz J 1975 IEEE Trans. Antennas Propag. 23 531
Google Scholar
[7] Luebbers R J, Kunz K 1992 IEEE Trans. Antennas Propag. 40 349
Google Scholar
[8] Van den Berghe S, Olyslager F, De Zutter D 1998 IEEE Microw. Guided Wave Lett. 8 75
Google Scholar
[9] Schild S, Chavannes N, Kuster N 2007 IEEE Trans. Antennas Propag. 55 3587
Google Scholar
[10] Wang Y, Langdon S 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI) Memphis, July 6–July 11, 2014 pp504–505
[11] Karlsson A 2009 IEEE Trans. Antennas Propag. 57 144
Google Scholar
[12] Nayyeri V, Soleimani M, Ramahi O M 2013 IEEE Trans. Electromagn. Compat. 56 385
Google Scholar
[13] Mi J, Ren Q, Su D 2020 IEEE Trans. Antennas Propag. 69 2230
Google Scholar
[14] Yang Q, Wei B, Li L, Ge D 2020 IEEE Trans. Antennas Propag. 69 3371
Google Scholar
[15] Ban Z G, Shi Y, Wang P 2021 IEEE Trans. Antennas Propag. 70 3916
Google Scholar
[16] Zhang T, Bao H, Gu P, Ding D, Werner D H, Chen R 2021 IEEE Trans. Antennas Propag. 70 526
Google Scholar
[17] Mitzner K 1968 IEEE Trans. Antennas Propag. 16 706
Google Scholar
[18] Li P, Shi Y, Jiang L J, Bağcι H 2015 IEEE Trans. Antennas Propag. 63 5686
Google Scholar
[19] Li P, Jiang L J, Bağcι H 2015 IEEE Trans. Antennas Propag. 63 3065
Google Scholar
[20] Li P, Jiang L J, Bağcı H 2018 IEEE Trans. Antennas Propag. 66 3590
Google Scholar
-
图 1 薄涂层示意图
Figure 1. Plane wave incident on a thin layer.
图 2 一维DGTD反射透射结果
Figure 2. The reflection and transmission coefficients (1D-DGTD).
图 3 薄层-四面体示意图 (DGTD)
Figure 3. Thin layer-tetrahedrons schematic (DGTD).
图 4 多薄层-四面体示意图(DGTD)
Figure 4. Thin layers-tetrahedrons schematic (DGTD).
图 5 一维DGTD反射透射结果
Figure 5. The reflection and transmission coefficients (1D-DGTD).
图 6 一维DGTD反射透射结果
Figure 6. The reflection and transmission coefficients (1D-DGTD).
图 7 一维模型示意图
Figure 7. One-dimensional model schematic.
图 8 一维DGTD反射透射结果
Figure 8. The reflection and transmission coefficients (1D-DGTD)
图 9 双薄层示意图
Figure 9. Thin layers schematic.
图 10 一维DGTD反射透射结果
Figure 10. The reflection and transmission coefficients (1D-DGTD).
图 11 双薄层示意图(一侧为介质层)
Figure 11. Thin layers with thick layer schematic.
图 12 一维DGTD反射透射结果
Figure 12. The reflection and transmission coefficients (1D-DGTD).
图 13 球形薄层
Figure 13. Spherical thin layer.
图 15 涂覆球
Figure 15. Spherical thin layer.
图 14 球形薄层单站RCS结果
Figure 14. Monostatic RCS of the spherical thin layer.
图 16 涂覆球单站RCS结果
Figure 16. Monostatic RCS of the coated sphere.
图 17 涂覆球(双层涂覆)
Figure 17. Coated sphere (double thin layers).
图 18 涂覆双层球单站RCS结果
Figure 18. Monostatic RCS of the coated sphere (double layers)
-
[1] Feliziani M 2011 IEEE Trans. Electromagn. Compat. 54 299
Google Scholar
[2] Hanson G W 2008 J. Appl. Phys. 103 064302
Google Scholar
[3] Shapoval O V, Gomez-Diaz J S, Perruisseau-Carrier J, Mosig J R, Nosich A I 2013 IEEE Trans. Terahertz Sci. Technol. 3 666
Google Scholar
[4] Maloney J G, Smith G S 1992 IEEE Trans. Antennas Propag. 40 323
Google Scholar
[5] Richmond J 1965 IEEE Trans. Antennas Propag. 13 334
Google Scholar
[6] Harrington R, Mautz J 1975 IEEE Trans. Antennas Propag. 23 531
Google Scholar
[7] Luebbers R J, Kunz K 1992 IEEE Trans. Antennas Propag. 40 349
Google Scholar
[8] Van den Berghe S, Olyslager F, De Zutter D 1998 IEEE Microw. Guided Wave Lett. 8 75
Google Scholar
[9] Schild S, Chavannes N, Kuster N 2007 IEEE Trans. Antennas Propag. 55 3587
Google Scholar
[10] Wang Y, Langdon S 2014 IEEE Antennas and Propagation Society International Symposium (APSURSI) Memphis, July 6–July 11, 2014 pp504–505
[11] Karlsson A 2009 IEEE Trans. Antennas Propag. 57 144
Google Scholar
[12] Nayyeri V, Soleimani M, Ramahi O M 2013 IEEE Trans. Electromagn. Compat. 56 385
Google Scholar
[13] Mi J, Ren Q, Su D 2020 IEEE Trans. Antennas Propag. 69 2230
Google Scholar
[14] Yang Q, Wei B, Li L, Ge D 2020 IEEE Trans. Antennas Propag. 69 3371
Google Scholar
[15] Ban Z G, Shi Y, Wang P 2021 IEEE Trans. Antennas Propag. 70 3916
Google Scholar
[16] Zhang T, Bao H, Gu P, Ding D, Werner D H, Chen R 2021 IEEE Trans. Antennas Propag. 70 526
Google Scholar
[17] Mitzner K 1968 IEEE Trans. Antennas Propag. 16 706
Google Scholar
[18] Li P, Shi Y, Jiang L J, Bağcι H 2015 IEEE Trans. Antennas Propag. 63 5686
Google Scholar
[19] Li P, Jiang L J, Bağcι H 2015 IEEE Trans. Antennas Propag. 63 3065
Google Scholar
[20] Li P, Jiang L J, Bağcı H 2018 IEEE Trans. Antennas Propag. 66 3590
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2872
- PDF Downloads: 47
- Cited By: 0
