-
Supported lipid bilayer (SLB) based biosensors possess biomedical applications such as in rapid detection of antigens and cytochromes. It is generally believed that the SLB can be formed by adsorbing and spontaneously rupturing vesicles on substrate. Recent findings highlight the importance of investigating the adsorption and rupture of individual vesicles during the SLB formation. Here, we use total internal reflection fluorescence microscopy (TIRFM) to characterize the spatiotemporal kinetics of the front spreading at patch boundary. Owing to the mixture of labeled and unlabeled vesicles individual vesicle or patch on the surface can be identified. The TIRFM is employed to investigate the adsorption, rupture of vesicles, and spreading of the patch front. Combining quartz crystal microbalance with dissipation monitoring (QCM-D) and TIRFM characterizations, we find that the size of vesicle has a significant effect on the front spreading at the patch boundary. Quantification of the number of patches and patches area displays that smaller vesicles are more prone to the formation of patches. The front spreading at the patch boundary is analyzed quantitatively using the average front growth velocity (
$ {v}_{\rm afv} $ ), which indicates that the$ {v}_{\rm afv} $ of 40-nm vesicles is one order of magnitude larger than that of the 112 nm vesicles. Both theoretical analysis and experimental observation show that the smaller vesicles can attain the higher concentration on the surface (C) and high diffusivity in the medium. The global growth theoretical model (GGM) presents that for the patches with the same surface area and vesicle exposure time, the growth of the patch depends on C and lipid loss percentage during the vesicle rupture. The calculated lipid loss of the smaller vesicles is slightly higher than that of the larger vesicles, while C plays a dominating role in determining the disparity of the patch growth between the different vesicles. This study promotes the understanding of the growth mechanism of patches on the surface. It demonstates the critcial role of the supply of vesicles in this process and provides an enlightenment for investigating the reassembly of lipids on a nanoscale.-
Keywords:
- vesicle size /
- surface concentration /
- front growth at patch boundary /
- global growth model
[1] Fu M F, Li J B 2018 Angew. Chem. Int. Ed. 57 11404
Google Scholar
[2] 王克青, 李自若, 费进波, 王晨蕾, 崔 巍, 赵 洁, 李峻柏 2021 高分子学报 52 1024
Google Scholar
Wang K Q, Li Z R, Fei J B, Wang C L, Cui W, Zhao J, Li J B 2021 Acta Polym. Sin. 52 1024
Google Scholar
[3] Kumar R K, Li M, Olof S N, Patil A J, Mann S 2013 Small 9 357
Google Scholar
[4] Xu Y Q, Fei J B, Li G L, Yuan T T, Li J B 2017 ACS Nano 11 10175
Google Scholar
[5] Ding H M, Yin Y W, Ni S D, Sheng Y J, Ma Y Q 2021 Chin. Phys. Lett. 38 018701
Google Scholar
[6] Jackman J A, Zhdanov V P, Cho N J 2014 Langmuir 30 9494
Google Scholar
[7] Richter R, Mukhopadhyay A, Brisson A 2003 Biophys. J. 85 3035
Google Scholar
[8] Keller C A, Glasmastar K, Zhdanov V P, Kasemo B 2000 Phys. Rev. Lett. 84 5443
Google Scholar
[9] Reimhult E, Hook F, Kasemo B 2002 J. Chem. Phys. 117 7401
Google Scholar
[10] Reimhult E, Hook F, Kasemo B 2003 Langmuir 19 1681
Google Scholar
[11] Zhu T, Jiang Z Y, Ma Y Q, Hu Y 2016 ACS Appl. Mater. Interfaces 8 5857
Google Scholar
[12] Hope M J, Walker D C, Cullis P R 1983 Biochem. Biophys. Res. Commun. 110 15
Google Scholar
[13] Seantier B, Kasemo B 2009 Langmuir 25 5767
Google Scholar
[14] Seantier B, Breffa C, Felix O, Decher G 2005 J. Phys. Chem. B 109 21755
Google Scholar
[15] Boudard S, Seantier B, Breffa C, Decher G, Felix O 2006 Thin Solid Films 495 246
Google Scholar
[16] Keller C A, Kasemo B 1998 Biophys. J. 75 1397
Google Scholar
[17] Roiter Y, Ornatska M, Rammohan A R, Balakrishnan J, Heine D R, Minko S 2008 Nano Lett. 8 941
Google Scholar
[18] Richter R P, Berat R, Brisson A R 2006 Langmuir 22 3497
Google Scholar
[19] Anderson T H, Min Y J, Weirich K L, Zeng H B, Fygenson D, Israelachvili J N 2009 Langmuir 25 6997
Google Scholar
[20] Jackman J A, Kim M C, Zhdanov V P, Cho N J 2016 Phys. Chem. Chem. Phys. 18 3065
Google Scholar
[21] 杨盼, 涂展春 2016 65 188701
Google Scholar
Yang P, Tu Z C 2016 Acta Phys. Sin. 65 188701
Google Scholar
[22] Reviakine I, Rossetti F F, Morozov A N, Textor M 2005 J. Chem. Phys. 122 204711
Google Scholar
[23] Reviakine I, Gallego M, Johannsmann D, Tellechea E 2012 J. Chem. Phys. 136 084702
Google Scholar
[24] Hatzakis N S, Bhatia V K, Larsen J, Madsen K L, Bolinger P Y, Kunding A H, Castillo J, Gether U, Hedegard P, Stamou D 2009 Nat. Chem. Biol. 5 835
Google Scholar
[25] Rabe M, Tabaei S R, Zetterberg H, Zhdanov V P, Hook F 2015 Angew. Chem. Int. Ed. 54 1022
Google Scholar
[26] Andrecka J, Spillane K M, Ortega-Arroyo J, Kukura P 2013 ACS Nano 7 10662
Google Scholar
[27] Weirich K L, Israelachvili J N, Fygenson D K 2010 Biophys. J. 98 85
Google Scholar
[28] Mapar M, Yoemetsa S, Pace H, Zhdanov V P, Agnarsson B, Hook F 2018 J. Phys. Chem. Lett. 9 5143
Google Scholar
[29] Xia Q S, Zhu T, Jiang Z Y, Ding H M, Ma Y Q 2020 Nanoscale 12 7804
Google Scholar
[30] 蒋中英, 张国梁, 马晶, 朱涛 2013 62 018701
Google Scholar
Jiang Z Y, Zhang G L, Ma J, Zhu T 2013 Acta Phys. Sin. 62 018701
Google Scholar
[31] Patty P J, Frisken B J 2003 Biophys. J. 85 996
Google Scholar
[32] Reimhult E, Zach M, Hook F, Kasemo B 2006 Langmuir 22 3313
Google Scholar
[33] Nabika H, Fukasawa A, Murakoshi K 2008 Phys. Chem. Chem. Phys. 10 2243
Google Scholar
-
图 1 支撑双层膜形成的动力学过程: 四张典型TIRFM照片显示了SLB形成过程的不同阶段. 第一次观测到的囊泡破裂用红色箭头标记表示形成了初始片层. 比例尺为20 μm
Figure 1. Spatiotemporal kinetics of the SLB formation: Four typical TIRFM images illustrating different stages of SLB formation. The first observed vesicle rupture is marked with red arrows to indicate the formation of the initial patch. The scale bar is 20 μm.
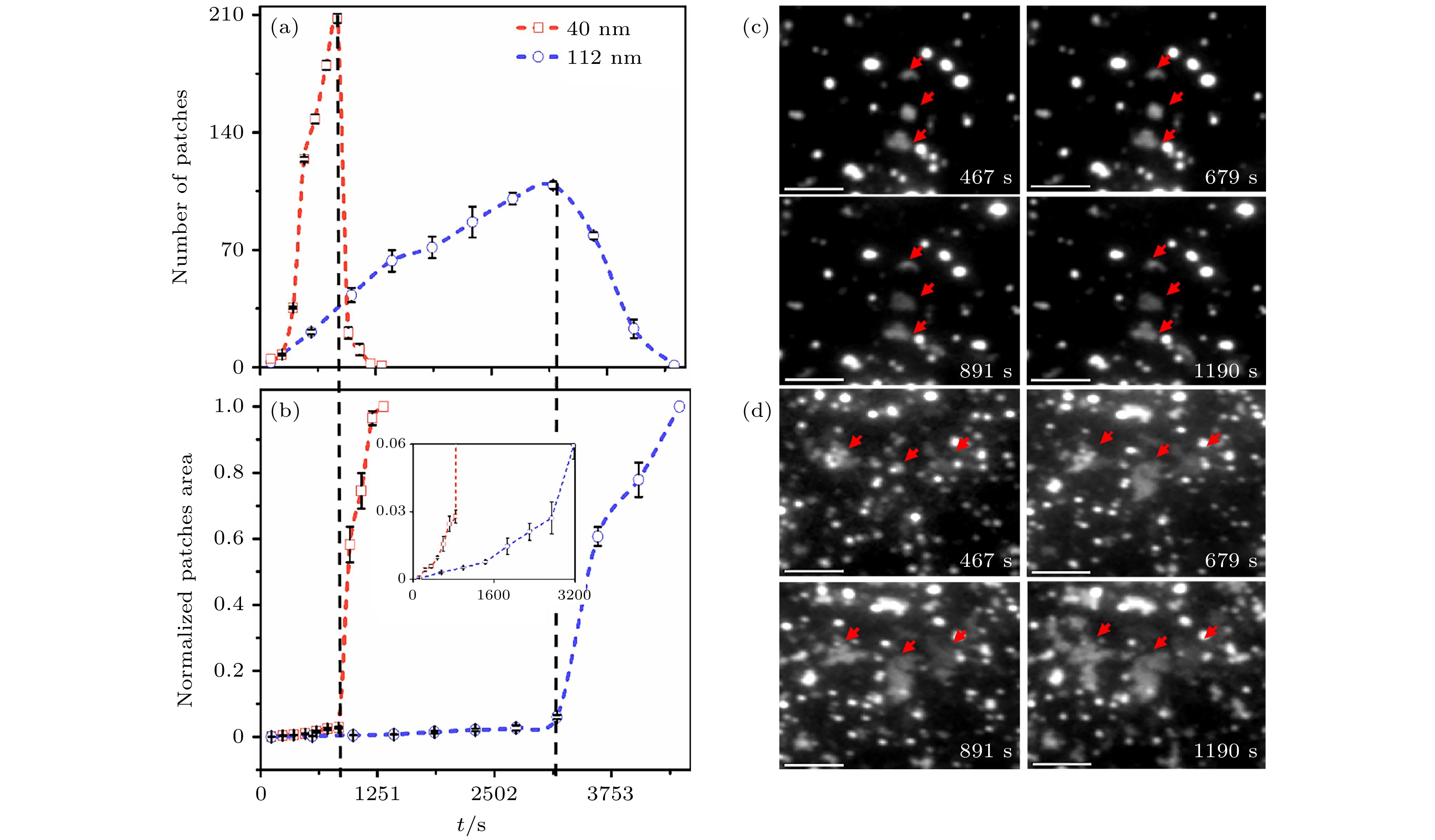
图 2 定量两种囊泡尺寸下, 片层成长动力学(统计区域为5812 μm2) (a) 片层数量随时间(t)变化; (b) 片层归一化面积随时间的变化, 插图为局域放大图; (c) 112 nm囊泡与 (d) 40 nm囊泡的TIRFM图像. 比例尺为20 μm
Figure 2. The kinetics of patch growth was quantitatively investigated using two vesicle samples with different sizes (Area of interest is 5812 μm2): (a) The number of patches changes with time (t); (b) the normalized area of patches changes with time. The inset shows the data on enlarged scales; TIRFM images of (c) 112 nm vesicles and (d) 40 nm vesicles. The scale bar is 20 μm.
图 3 片层成长期间观察到的代表性图像以及
$ {v}_{\mathrm{a}\mathrm{f}\mathrm{v}} $ 对时间的依赖性, 颜色指代了其前沿的成长速度 (a) 112 nm囊泡; (b) 40 nm囊泡. 比例尺为20 μmFigure 3. Representative images observed during the patch growth and the dependence of
$ {v}_{\mathrm{a}\mathrm{f}\mathrm{v}} $ on t, colors refer to the growth rate of patch boundary: (a) 112 nm vesicles; (b) 40 nm vesicles. The scale bar is 20 μm.
图 4 (a) 通过TIRFM表征不同尺寸囊泡初始片层形成、片层数量达到峰值及完全成膜的时间; (b) 囊泡数量与随时间变化(统计区域为5812 µm2); (c) 通过QCM-D表征不同尺寸囊泡的吸附与成膜
Figure 4. (a) The time spent for the initial patch formation, the maximum of patch number, and complete SLB formation using vesicles with different sizes, characterized by TIRFM; (b) The number of vesicles changes with time (The area of interest is 5812 µm2); (c) The vesicle-to-SLB transformation using vesicles with different sizes, characterized by QCM-D.
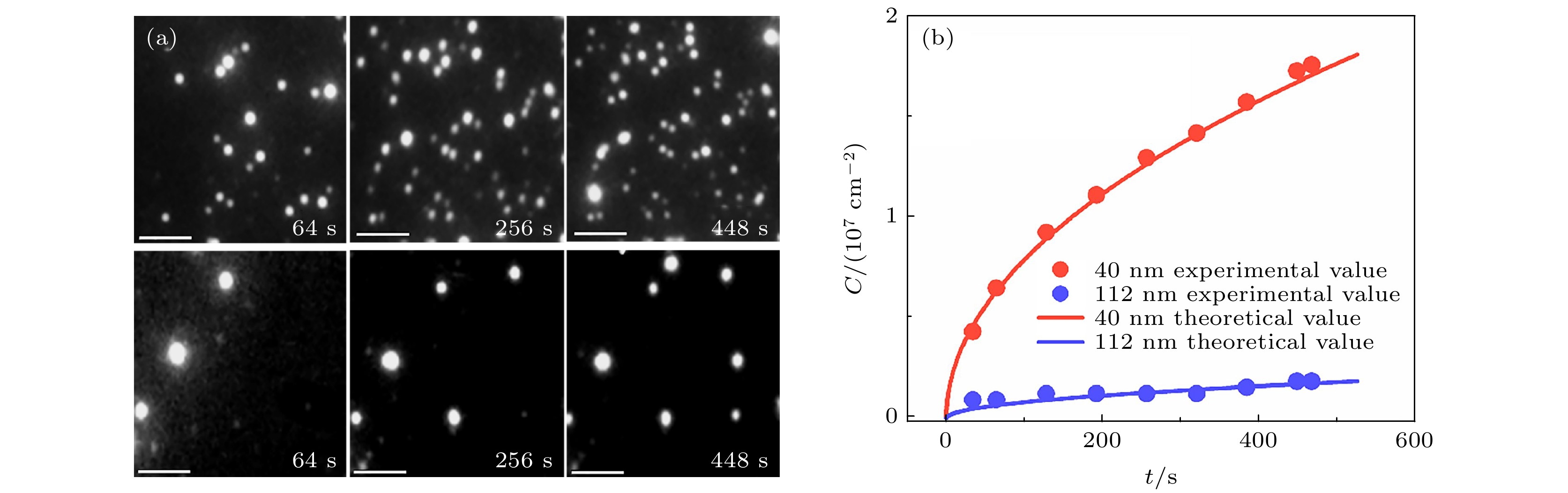
图 5 扩散受限的囊泡吸附动力学 (a) 40 nm (上)和112 nm (下)的囊泡表面浓度随时间变化的TIRFM图像; (b) 吸附囊泡数量的实验统计与理论计算值. 比例尺为20 μm
Figure 5. Diffusion-limited kinetics of vesicle adsorption: (a) TIRFM images of surface-attached vesicles, whose concentration changes with time. Vesicle diameter = 40 nm (upper) and 112 nm (lower); (b) Experimental statistics and theoretical estimation of the number of adsorbed vesicles. The scale bar is 20 μm.
图 6 片层的半径随kt的变化 (a)选用的40和112 nm囊泡形成的片层; (b) 两种尺寸囊泡的片层成长的全局(实线)和局域(虚线)模型拟合. 比例尺为20 μm
Figure 6. Radius of the patch changes as a function of kt: (a) Patches formed by 40 and 112 nm vesicles; (b) fit of the experimental data to the GGM and LGM using the vesicles with two sizes. The scale bar is 20 μm.
-
[1] Fu M F, Li J B 2018 Angew. Chem. Int. Ed. 57 11404
Google Scholar
[2] 王克青, 李自若, 费进波, 王晨蕾, 崔 巍, 赵 洁, 李峻柏 2021 高分子学报 52 1024
Google Scholar
Wang K Q, Li Z R, Fei J B, Wang C L, Cui W, Zhao J, Li J B 2021 Acta Polym. Sin. 52 1024
Google Scholar
[3] Kumar R K, Li M, Olof S N, Patil A J, Mann S 2013 Small 9 357
Google Scholar
[4] Xu Y Q, Fei J B, Li G L, Yuan T T, Li J B 2017 ACS Nano 11 10175
Google Scholar
[5] Ding H M, Yin Y W, Ni S D, Sheng Y J, Ma Y Q 2021 Chin. Phys. Lett. 38 018701
Google Scholar
[6] Jackman J A, Zhdanov V P, Cho N J 2014 Langmuir 30 9494
Google Scholar
[7] Richter R, Mukhopadhyay A, Brisson A 2003 Biophys. J. 85 3035
Google Scholar
[8] Keller C A, Glasmastar K, Zhdanov V P, Kasemo B 2000 Phys. Rev. Lett. 84 5443
Google Scholar
[9] Reimhult E, Hook F, Kasemo B 2002 J. Chem. Phys. 117 7401
Google Scholar
[10] Reimhult E, Hook F, Kasemo B 2003 Langmuir 19 1681
Google Scholar
[11] Zhu T, Jiang Z Y, Ma Y Q, Hu Y 2016 ACS Appl. Mater. Interfaces 8 5857
Google Scholar
[12] Hope M J, Walker D C, Cullis P R 1983 Biochem. Biophys. Res. Commun. 110 15
Google Scholar
[13] Seantier B, Kasemo B 2009 Langmuir 25 5767
Google Scholar
[14] Seantier B, Breffa C, Felix O, Decher G 2005 J. Phys. Chem. B 109 21755
Google Scholar
[15] Boudard S, Seantier B, Breffa C, Decher G, Felix O 2006 Thin Solid Films 495 246
Google Scholar
[16] Keller C A, Kasemo B 1998 Biophys. J. 75 1397
Google Scholar
[17] Roiter Y, Ornatska M, Rammohan A R, Balakrishnan J, Heine D R, Minko S 2008 Nano Lett. 8 941
Google Scholar
[18] Richter R P, Berat R, Brisson A R 2006 Langmuir 22 3497
Google Scholar
[19] Anderson T H, Min Y J, Weirich K L, Zeng H B, Fygenson D, Israelachvili J N 2009 Langmuir 25 6997
Google Scholar
[20] Jackman J A, Kim M C, Zhdanov V P, Cho N J 2016 Phys. Chem. Chem. Phys. 18 3065
Google Scholar
[21] 杨盼, 涂展春 2016 65 188701
Google Scholar
Yang P, Tu Z C 2016 Acta Phys. Sin. 65 188701
Google Scholar
[22] Reviakine I, Rossetti F F, Morozov A N, Textor M 2005 J. Chem. Phys. 122 204711
Google Scholar
[23] Reviakine I, Gallego M, Johannsmann D, Tellechea E 2012 J. Chem. Phys. 136 084702
Google Scholar
[24] Hatzakis N S, Bhatia V K, Larsen J, Madsen K L, Bolinger P Y, Kunding A H, Castillo J, Gether U, Hedegard P, Stamou D 2009 Nat. Chem. Biol. 5 835
Google Scholar
[25] Rabe M, Tabaei S R, Zetterberg H, Zhdanov V P, Hook F 2015 Angew. Chem. Int. Ed. 54 1022
Google Scholar
[26] Andrecka J, Spillane K M, Ortega-Arroyo J, Kukura P 2013 ACS Nano 7 10662
Google Scholar
[27] Weirich K L, Israelachvili J N, Fygenson D K 2010 Biophys. J. 98 85
Google Scholar
[28] Mapar M, Yoemetsa S, Pace H, Zhdanov V P, Agnarsson B, Hook F 2018 J. Phys. Chem. Lett. 9 5143
Google Scholar
[29] Xia Q S, Zhu T, Jiang Z Y, Ding H M, Ma Y Q 2020 Nanoscale 12 7804
Google Scholar
[30] 蒋中英, 张国梁, 马晶, 朱涛 2013 62 018701
Google Scholar
Jiang Z Y, Zhang G L, Ma J, Zhu T 2013 Acta Phys. Sin. 62 018701
Google Scholar
[31] Patty P J, Frisken B J 2003 Biophys. J. 85 996
Google Scholar
[32] Reimhult E, Zach M, Hook F, Kasemo B 2006 Langmuir 22 3313
Google Scholar
[33] Nabika H, Fukasawa A, Murakoshi K 2008 Phys. Chem. Chem. Phys. 10 2243
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 3589
- PDF Downloads: 60
- Cited By: 0
