-
An asymmetric envelope function for modulating the spectrum of circular Airy beam is proposed in this work. The propagation properties of the modified circular Airy beam are investigated in both theory and experiment. The three parameters of the asymmetric hyperbolic secant function can be used to adjust the ratio of the high frequency components to the low frequency components in Fourier space, and thus tuning the propagation properties of this modified circular Airy beam. The results demonstrate that the focal position is affected mainly by the high frequency components. The maximum focal intensity will not be enhanced continuously by increasing the proportion of the high frequency components. It depends on the ratio of the high frequency components to the low frequency components when the center frequency is determined. Therefore, using an asymmetric envelope in Fourier space is much more reasonable than using the high pass filtering or symmetric Gaussian envelope. The FWHM decreases significantly with the increase of center frequency. When the parameters are chosen appropriately, the size of focal spot will be reduced significantly, the maximum focal intensity, especially the abruptly autofocusing property will be enhanced greatly and the focal position can remain almost the same as the focal position of the common circular Airy beam. The maximum focal intensity of the proposed beam is 3.4 times that of the common circular Airy beam and the abruptly autofocusing property of the proposed beam is much better than that of the beam using the symmetric Gaussian envelope. The phase-only encoding method in Fourier space is used to generate the proposed beam in experiment. The experimental results are in reasonable agreement with the simulation results. It indicates that the modified beam can be generated conveniently by using the same method as that used to generate the common circular Airy beam.
[1] Siviloglou G A, Christodoulides D N 2007 Opt. Lett. 32 979
Google Scholar
[2] Siviloglou G A, Broky J, Dogariu A, Christodoulides D N 2007 Phys. Rev. Lett. 99 213901
Google Scholar
[3] Qian J, Liu B Y, Sun H X, Yuan S Q, Yu X Z 2017 Chin. Phys. B 26 114304
Google Scholar
[4] 崔省伟, 陈子阳, 胡克磊, 蒲继雄 2013 62 094205
Google Scholar
Cui S W, Chen Z Y, Hu K L, Pu J X 2013 Acta Phys. Sin. 62 094205
Google Scholar
[5] 张泽, 刘京郊, 张鹏, 倪培根, Prakash J, 胡洋, 姜东升, Christodoulides D N, 陈志刚 2013 62 034209
Google Scholar
Zhang Z, Liu J J, Zhang P, Ni P G, Prakash J, Hu Y, Jiang D S, Christodoulides D N, Chen Z G 2013 Acta Phys. Sin. 62 034209
Google Scholar
[6] Efremidis N K, Christodoulides D N 2010 Opt. Lett. 35 4045
Google Scholar
[7] Gu Y L, Gbur G 2010 Opt. Lett. 35 3456
Google Scholar
[8] Khonina S N, Ustinov A V 2017 J. Opt. Soc. Am. A 34 1991
Google Scholar
[9] Papazoglou D G, Efremidis N K, Christodoulides D N, Tzortzakis S 2011 Opt. Lett. 36 1842
Google Scholar
[10] Lu W, Sun X, Chen H, Liu S, Lin Z 2019 Phys. Rev. A 99 013817
Google Scholar
[11] Jiang Y, Huang K, Lu X 2013 Opt. Express 21 24413
Google Scholar
[12] Koulouklidis A D, Papazoglou D G, Fedorov V Y, Tzortzakis S 2017 Phys. Rev. Lett. 119 223901
Google Scholar
[13] Fedorov V Y, Papazoglou D G, Tzortzakis S 2019 Opt. Lett. 44 2974
Google Scholar
[14] Panagiotopoulos P, Papazoglou D G, Couairon A, Tzortzakis S 2013 Nat. Commun. 4 2622
Google Scholar
[15] Liu K, Koulouklidis A D, Papazoglou D G, Tzortzakis S, Zhang X C 2016 Optica 3 605
Google Scholar
[16] Li N, Jiang Y, Huang K, Lu X 2014 Opt. Express 22 22847
Google Scholar
[17] Jiang Y, Zhu X, Yu W, Shao H, Zheng W, Lu X 2015 Opt. Express 23 29834
Google Scholar
[18] Zhong H, Zhang Y, Beli¢ M R, Li C, Wen F, Zhang Z, Zhang Y 2016 Opt. Express 24 7495
Google Scholar
[19] Porfirev A P, Khonina S N 2017 J. Opt. Soc. Am. B 34 2544
Google Scholar
[20] Li T, Zhang X, Huang K, Lu X 2021 Opt. Laser Technol. 137 106814
Google Scholar
[21] Geng T, Zhang X X 2020 Opt. Express 28 2447
Google Scholar
[22] Chremmos I, Zhang P, Prakash J, Efremidis N K, Christodoulides D N, Chen Z 2011 Opt. Lett. 36 3675
Google Scholar
[23] Magni V, Cerullo G, De Silvestri S 1992 J. Opt. Soc. Am. A 9 2031
Google Scholar
-
图 1 参数
${r_0} = 1\;{\text{mm}}$ ,$w = $ 0.1 mm,$\alpha = 0.1$ 时 (a) CAB 的频谱$ F\left( k \right) $ ; (b) CAB频谱的绝对值$\left| {F\left( k \right)} \right|$ 及其包络曲线${E_{\text{V}}}\left( k \right)$ Figure 1. Calculation results of (a)
$ F\left( k \right) $ , (b)$\left| {F\left( k \right)} \right|$ and${E_{\text{V}}}\left( k \right)$ with${r_0} = 1\;{\text{mm}}$ ,$w = $ 0.1 mm and$\alpha = 0.1$ .
图 2 不同调制参数的AMCAB的频谱分布以及相对应的初始面光强分布 (a)
$ {\gamma _1} = 3\;{\text{m}}{{\text{m}}^{ - 1}} $ ,$ {\gamma _2} = 1.5\;{\text{m}}{{\text{m}}^{ - 1}} $ 保持不变,$\beta $ 不同时的频谱分布及相对应的(b)初始面光强分布; (c)$ \beta = 7\;{\text{m}}{{\text{m}}^{ - 1}} $ 、$ {\gamma _2} = 1\;{\text{m}}{{\text{m}}^{ - 1}} $ 保持不变,$ {\gamma _1} $ 不同时的频谱分布及相对应的(d)初始面光强分布; (e)$ \beta = 7\;{\text{m}}{{\text{m}}^{ - 1}} $ ,$ {\gamma _1} = 1\;{\text{m}}{{\text{m}}^{ - 1}} $ 保持不变,$ {\gamma _2} $ 不同时的频谱分布及相对应的(f)初始面光强分布Figure 2. Spectrum distributions and corresponding intensity distributions of AMCAB at the initial plane with different parameters. (a) Spectrum distributions and (b) corresponding intensity distributions with different
$\beta $ when$ {\gamma _1} = 3\;{\text{m}}{{\text{m}}^{ - 1}} $ ,$ {\gamma _2} = 1.5\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (c) spectrum distributions and (d) corresponding intensity distributions with different$ {\gamma _1} $ when$ \beta = 7\;{\text{m}}{{\text{m}}^{ - 1}} $ ,$ {\gamma _2} = 1\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (e) Spectrum distributions and (f) corresponding intensity distributions with different$ {\gamma _2} $ when$ \beta = 7\;{\text{m}}{{\text{m}}^{ - 1}} $ ,$ {\gamma _1} = 1\;{\text{m}}{{\text{m}}^{ - 1}} $ .
图 3 CAB和AMCAB的侧面光强分布 (a) CAB; (b)
$\beta = $ $ 8.3\;{\text{m}}{{\text{m}}^{ - 1}}$ ,${\gamma _{\text{1}}} = 5.5\;{\text{m}}{{\text{m}}^{ - 1}}$ ,${\gamma _{\text{2}}} = 0.1\;{\text{m}}{{\text{m}}^{ - 1}}$ 的AMCABFigure 3. Propagation dynamics of CAB and AMCAB: (a) CAB; (b) AMCAB with
$\beta = 8.3\;{\text{m}}{{\text{m}}^{ - 1}}$ ,${\gamma _{\text{1}}} = 5.5\;{\text{m}}{{\text{m}}^{ - 1}}$ and${\gamma _{\text{2}}} = 0.1\;{\text{m}}{{\text{m}}^{ - 1}}$ .
图 4
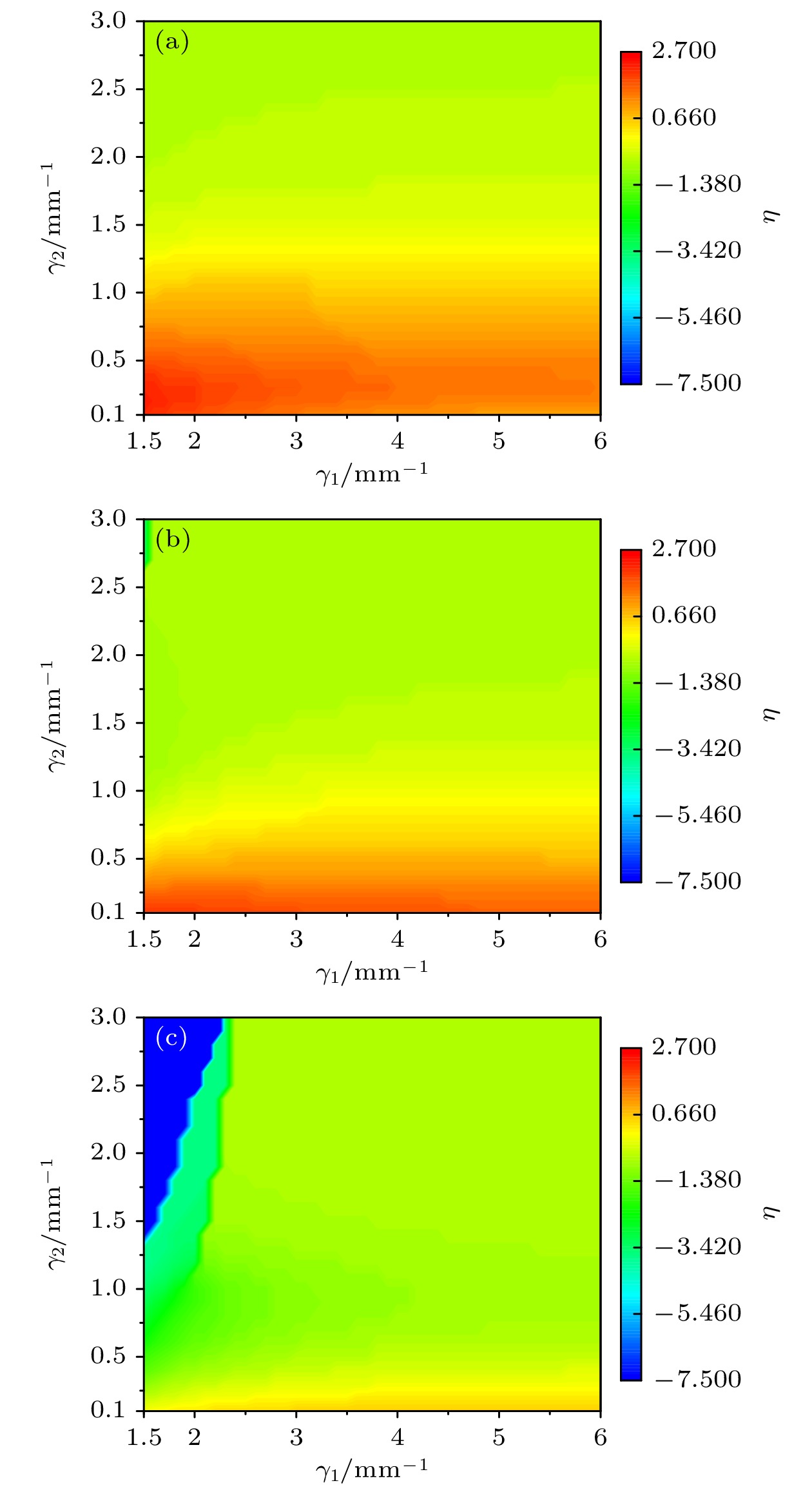
$\beta $ 不同时, AMCAB和CAB的相对焦距差$ \eta $ 随${\gamma _1}$ ,${\gamma _2}$ 的变化情况 (a)$ \beta = 6\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (b)$ \beta = 7\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (c)$\beta = $ $ 8\;{\text{m}}{{\text{m}}^{ - 1}}$ Figure 4. The relative focal distance difference between the CAB and the AMCAB as a function of
${\gamma _1}$ and${\gamma _2}$ with different$\beta $ . (a)$ \beta = 6\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (b)$ \beta = 7\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (c)$\beta = $ $ 8\;{\text{m}}{{\text{m}}^{ - 1}}$ .
图 5
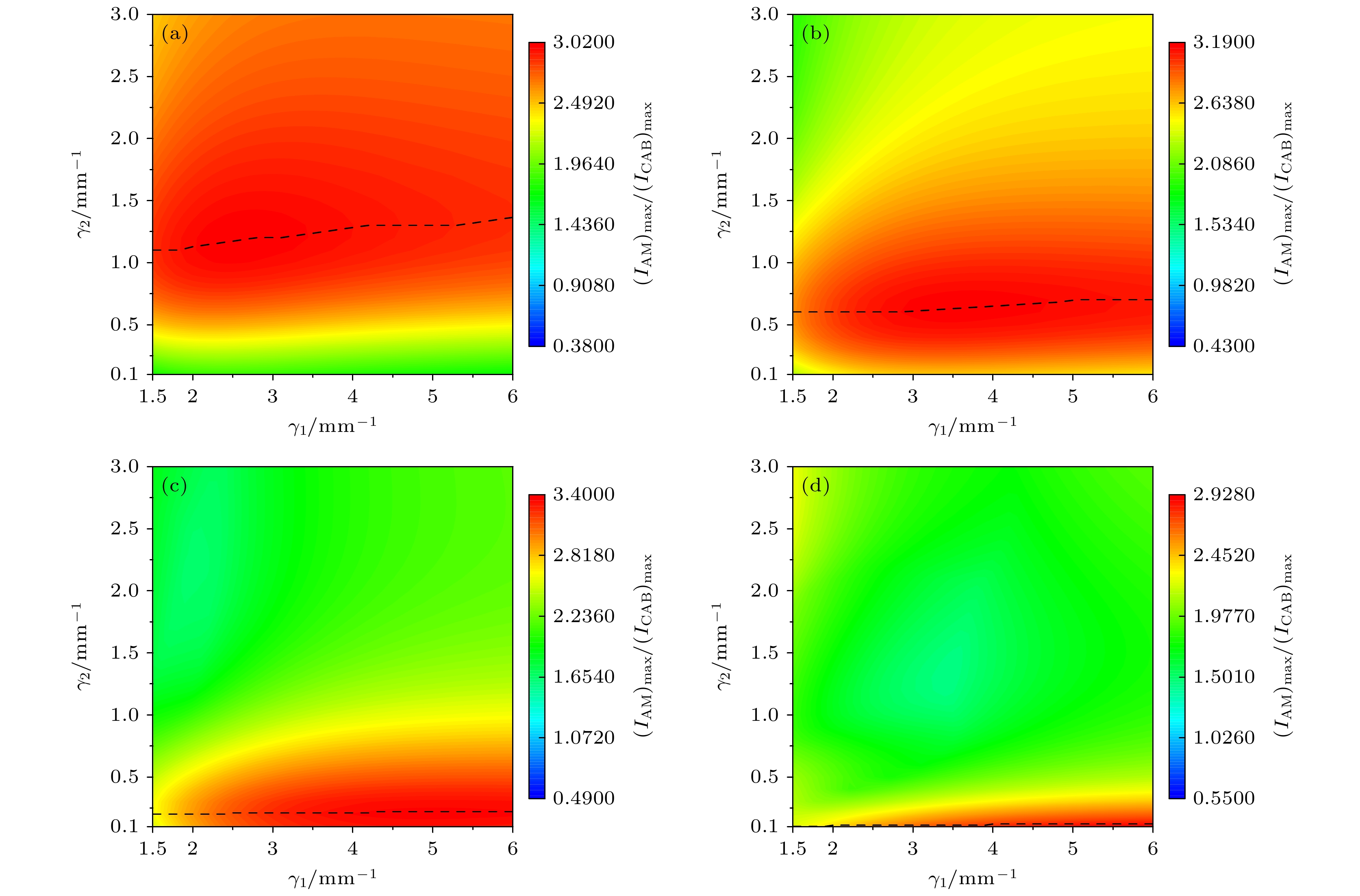
$\beta $ 不同时, AMCAB和CAB的焦点光强比值随${\gamma _1}$ ,${\gamma _2}$ 的变化情况, 其中虚线为光强比值的极大值位置随${\gamma _1}$ 和$ {\gamma _2} $ 的变化曲线 (a)$ \beta = 6\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (b)$ \beta = 7\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (c)$ \beta = 8\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (d)$ \beta = 9\;{\text{m}}{{\text{m}}^{ - 1}} $ Figure 5. The maximum focal intensity contrast between the AMCAB and the CAB as a function of
${\gamma _1}$ and${\gamma _2}$ with different$\beta $ . Here, the dash lines show the positions of the maximum values as a function of${\gamma _1}$ and$ {\gamma _2} $ . (a)$ \beta = 6\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (b)$ \beta = 7\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (c)$\beta = $ $ 8\;{\text{m}}{{\text{m}}^{ - 1}}$ ; (d)$ \beta = 9\;{\text{m}}{{\text{m}}^{ - 1}} $ .
图 6 不同参数的AMCAB在焦平面上的归一化光强分布 (a)
$ {\gamma _1} = 3\;{\text{m}}{{\text{m}}^{ - 1}} $ ,$ {\gamma _2} = 1.5\;{\text{m}}{{\text{m}}^{ - 1}} $ 时, 不同$\beta $ 的AMCAB; (b)$ \beta = 7\;{\text{m}}{{\text{m}}^{ - 1}} $ ,$ {\gamma _2} = 1\;{\text{m}}{{\text{m}}^{ - 1}} $ 时, 不同$ {\gamma _1} $ 的AMCAB; (c)$ \beta = 6\;{\text{m}}{{\text{m}}^{ - 1}} $ ,$ {\gamma _1} = 1\;{\text{m}}{{\text{m}}^{ - 1}} $ 时, 不同$ {\gamma _2} $ 的AMCAB.Figure 6. Normalized intensity distributions of AMCAB with different parameters at the focal plane: (a) AMCAB with different
$\beta $ when$ {\gamma _1} = 3\;{\text{m}}{{\text{m}}^{ - 1}} $ ,$ {\gamma _2} = 1.5\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (b) AMCAB with different$ {\gamma _1} $ when$ \beta = 7\;{\text{m}}{{\text{m}}^{ - 1}} $ ,$ {\gamma _2} = 1\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (c) AMCAB with different$ {\gamma _2} $ when$ \beta = 6\;{\text{m}}{{\text{m}}^{ - 1}} $ ,${\gamma _1} = $ $ 1\;{\text{m}}{{\text{m}}^{ - 1}}$ .
图 7 不同参数的AMCAB沿z轴的
${I_C}$ 分布仿真结果 (a)${\gamma _1} = 3\;{\text{m}}{{\text{m}}^{ - 1}}$ ,$ {\gamma _2} = 1.5\;{\text{m}}{{\text{m}}^{ - 1}} $ 时, 不同$\beta $ 的AMCAB; (b)$ \beta = 6\;{\text{m}}{{\text{m}}^{ - 1}} $ ,$ {\gamma _2} = 1.5\;{\text{m}}{{\text{m}}^{ - 1}} $ 时, 不同$ {\gamma _1} $ 的AMCAB; (c)$ \beta = 6\;{\text{m}}{{\text{m}}^{ - 1}} $ ,${\gamma _1} = 1\;{\text{m}}{{\text{m}}^{ - 1}}$ 时, 不同$ {\gamma _2} $ 的AMCAB.Figure 7. Simulated results of on-axis intensity contrast
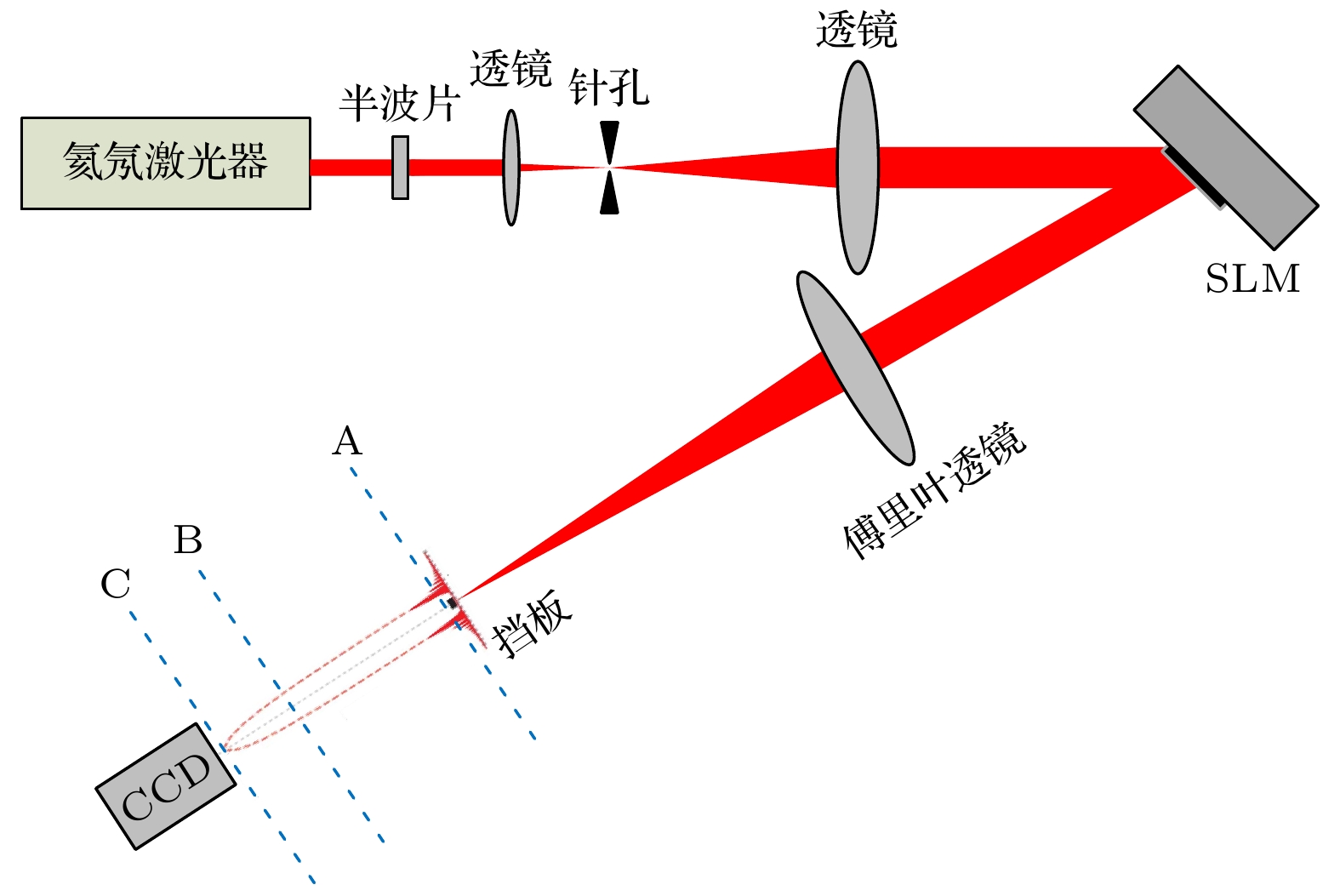
${I_C}$ of AMCAB with different parameters. (a) AMCAB with different$\beta $ when${\gamma _1} = 3\;{\text{m}}{{\text{m}}^{ - 1}}$ ,$ {\gamma _2} = 1.5\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (b) AMCAB with different$ {\gamma _1} $ when$ \beta = 6\;{\text{m}}{{\text{m}}^{ - 1}} $ ,$ {\gamma _2} = 1.5\;{\text{m}}{{\text{m}}^{ - 1}} $ ; (c) AMCAB with different$ {\gamma _2} $ when$ \beta = 6\;{\text{m}}{{\text{m}}^{ - 1}} $ ,${\gamma _1} = 1\;{\text{m}}{{\text{m}}^{ - 1}}$ .
图 8 实验光路示意图
Figure 8. Diagram of experimental setup.
图 9 初始面光强分布的实验(虚线)和仿真(实线)结果以及相应的加载于SLM上的相位分布图 (a) CAB的归一化径向光强分布和(b)二维光强分布实验结果以及(c)SLM上加载的相位分布; (d)
$ \beta = 6\;{\text{m}}{{\text{m}}^{ - 1}} $ ,${\gamma _{\text{1}}} = 2.3\;{\text{m}}{{\text{m}}^{ - 1}}$ ,${\gamma _{\text{2}}} = 0.8\;{\text{m}}{{\text{m}}^{ - 1}}$ 时, AMCAB的归一化径向光强分布和(e)二维光强分布实验结果以及(f)SLM上加载的相位分布; (g)$ \beta = 8.3\;{\text{m}}{{\text{m}}^{ - 1}} $ ,${\gamma _{\text{1}}} = 5.5\;{\text{m}}{{\text{m}}^{ - 1}}$ ,${\gamma _{\text{2}}} = 0.1\;{\text{m}}{{\text{m}}^{ - 1}}$ 时, AMCAB的归一化径向光强分布和(h)二维光强分布实验结果以及(i) SLM上加载的相位分布Figure 9. Phase masks on the SLM, experimental (dash line) and simulated (solid line) results of normalized intensity distributions profiles at initial plane: (a) Radial intensity distributions and (b) measured 2D intensity distributions of CAB, and (c) corresponding phase mask on the SLM; (d) radial intensity distributions and (e) measured 2D intensity distributions of AMCAB with
$ \beta = 6\;{\text{m}}{{\text{m}}^{ - 1}} $ ,${\gamma _{\text{1}}} = 2.3\;{\text{m}}{{\text{m}}^{ - 1}}$ ,${\gamma _{\text{2}}} = 0.8\;{\text{m}}{{\text{m}}^{ - 1}}$ , and (f) corresponding phase mask on the SLM; (g) radial intensity distributions and (h) measured 2D intensity distributions of AMCAB with$ \beta = 8.3\;{\text{m}}{{\text{m}}^{ - 1}} $ ,${\gamma _{\text{1}}} = 5.5\;{\text{m}}{{\text{m}}^{ - 1}}$ ,${\gamma _{\text{2}}} = 0.1\;{\text{m}}{{\text{m}}^{ - 1}}$ , and (i) corresponding phase mask on the SLM.
图 10 参数
$ \beta = 8.3\;{\text{m}}{{\text{m}}^{ - 1}} $ ,${\gamma _{\text{1}}} = 5.5\;{\text{m}}{{\text{m}}^{ - 1}}$ ,${\gamma _{\text{2}}} = 0.1\;{\text{m}}{{\text{m}}^{ - 1}}$ 时, AMCAB在不同截面光强分布的实验(虚线)和仿真(实线)结果, 其中${I_{\max }}\left( 0 \right)$ 为初始面光强峰值 (a)$z = 400\;{\text{mm}}$ 处的径向光强比值分布和相应的(b)二维光强分布实验结果; (c)焦平面($z = 655\;{\text{mm}}$ )处的径向光强比值分布和相应的(d)二维光强分布实验结果Figure 10. Experimental (dash line) and simulated (solid line) results of intensity contrast
$ I/{I_{\max }}(0) $ of AMCAB with$ \beta = 8.3\;{\text{m}}{{\text{m}}^{ - 1}} $ ,${\gamma _{\text{1}}} = 5.5\;{\text{m}}{{\text{m}}^{ - 1}}$ ,${\gamma _{\text{2}}} = 0.1\;{\text{m}}{{\text{m}}^{ - 1}}$ at different propagation planes: (a) Radial intensity contrast and (b) corresponding measured 2D intensity distributions at$z = 400\;{\text{mm}}$ ; (c) radial intensity contrast and (d) the corresponding measured 2D intensity distributions at the focal plane ($z = 655\;{\text{mm}}$ ).表 1 CAB与GCAB, AMCAB最佳调制结果的比较
Table 1. The optimized results of GCAB and AMCAB, and the results of CAB are also presented for comparison.
光束
类型$ {I_{\max }}/{\left( {{I_{\rm CAB}}} \right)_{\max }} $ $( I_{\rm{C} })_{\max } = $$ I_{\max }/I_{\max} (0)$ 焦斑F
WHM/μmCAB 1 52 38 GCAB[21] 2.9 694 34 AMCAB 3.4 1369 29 注: ${I_{\max }}$为焦点最大光强, $ {\left( {{I_{{\text{CAB}}}}} \right)_{\max }} $为CAB焦点最大光强, $ {I_{\max }}\left( 0 \right) $为初始面最大光强 
DownLoad: CSV
-
[1] Siviloglou G A, Christodoulides D N 2007 Opt. Lett. 32 979
Google Scholar
[2] Siviloglou G A, Broky J, Dogariu A, Christodoulides D N 2007 Phys. Rev. Lett. 99 213901
Google Scholar
[3] Qian J, Liu B Y, Sun H X, Yuan S Q, Yu X Z 2017 Chin. Phys. B 26 114304
Google Scholar
[4] 崔省伟, 陈子阳, 胡克磊, 蒲继雄 2013 62 094205
Google Scholar
Cui S W, Chen Z Y, Hu K L, Pu J X 2013 Acta Phys. Sin. 62 094205
Google Scholar
[5] 张泽, 刘京郊, 张鹏, 倪培根, Prakash J, 胡洋, 姜东升, Christodoulides D N, 陈志刚 2013 62 034209
Google Scholar
Zhang Z, Liu J J, Zhang P, Ni P G, Prakash J, Hu Y, Jiang D S, Christodoulides D N, Chen Z G 2013 Acta Phys. Sin. 62 034209
Google Scholar
[6] Efremidis N K, Christodoulides D N 2010 Opt. Lett. 35 4045
Google Scholar
[7] Gu Y L, Gbur G 2010 Opt. Lett. 35 3456
Google Scholar
[8] Khonina S N, Ustinov A V 2017 J. Opt. Soc. Am. A 34 1991
Google Scholar
[9] Papazoglou D G, Efremidis N K, Christodoulides D N, Tzortzakis S 2011 Opt. Lett. 36 1842
Google Scholar
[10] Lu W, Sun X, Chen H, Liu S, Lin Z 2019 Phys. Rev. A 99 013817
Google Scholar
[11] Jiang Y, Huang K, Lu X 2013 Opt. Express 21 24413
Google Scholar
[12] Koulouklidis A D, Papazoglou D G, Fedorov V Y, Tzortzakis S 2017 Phys. Rev. Lett. 119 223901
Google Scholar
[13] Fedorov V Y, Papazoglou D G, Tzortzakis S 2019 Opt. Lett. 44 2974
Google Scholar
[14] Panagiotopoulos P, Papazoglou D G, Couairon A, Tzortzakis S 2013 Nat. Commun. 4 2622
Google Scholar
[15] Liu K, Koulouklidis A D, Papazoglou D G, Tzortzakis S, Zhang X C 2016 Optica 3 605
Google Scholar
[16] Li N, Jiang Y, Huang K, Lu X 2014 Opt. Express 22 22847
Google Scholar
[17] Jiang Y, Zhu X, Yu W, Shao H, Zheng W, Lu X 2015 Opt. Express 23 29834
Google Scholar
[18] Zhong H, Zhang Y, Beli¢ M R, Li C, Wen F, Zhang Z, Zhang Y 2016 Opt. Express 24 7495
Google Scholar
[19] Porfirev A P, Khonina S N 2017 J. Opt. Soc. Am. B 34 2544
Google Scholar
[20] Li T, Zhang X, Huang K, Lu X 2021 Opt. Laser Technol. 137 106814
Google Scholar
[21] Geng T, Zhang X X 2020 Opt. Express 28 2447
Google Scholar
[22] Chremmos I, Zhang P, Prakash J, Efremidis N K, Christodoulides D N, Chen Z 2011 Opt. Lett. 36 3675
Google Scholar
[23] Magni V, Cerullo G, De Silvestri S 1992 J. Opt. Soc. Am. A 9 2031
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4343
- PDF Downloads: 97
- Cited By: 0
