-
Sulfur oxide (SO) is a kind of well-known diatomic molecule which becomes one of the major pollutants in the atmosphere. Control of the heat capacity of SO molecule is of great significance for elucidating its macroscopic evolution process. In the research of macroscopic systems composed of many particles as well as several matters, it is an important approach to obtain macroscopic thermodynamic quantities of the system by constructing a partition function from the microscopic information of molecule. For diatomic molecules in a certain electronic state, the partition function can directly be obtained by calculating the rovibrational energy of the system to acquire the macroscopic molar heat capacities. In this work, the contribution of rotational behavior to molar heat capacity is further considered. The potential energy function for the ground electronic state of SO is constructed by the variational algebraic method (VAM) and RKR (Rydberg-Klein-Rees) method, in which the former one can determine the complete vibrational energy levels of an electronic state of a molecule. The rovibrational energy level of the system is obtained by analytical solution, and then the molar heat capacity of SO macroscopic gas in the temperature range of 300–6000 K is calculated by quantum statistical ensemble theory The above calculation depends only on the experimental vibrational energy, experimental rotational spectral constant and the dissociation energy of SO molecule. Fortunately, through comparison between theoretical calculation results and experimental data, we find that the molar heat capacity of gaseous SO molecule can be well predicted by employing the full set of rovibrational energy to describe the internal vibration and rotation of SO molecule. The idea of calculating the molar heat capacity by using the full set of rovibrational energy makes up for the shortcomings of previous work where molar heat capacity is calculated by using the approximate model characterizing the molecular rotational behavior, and also provides a new research paradigm for solving macro thermodynamic quantities based on micro statistical processes . -
Keywords:
- SO /
- variational algebraic method /
- rovibrational energies /
- molar heat capacities
[1] McBride B J, Zehe M J, Gordon S 2002 NASA Glenn Coefficients for Calculating Thermodynamic Properties of Individual Species (Cleveland: National Aeronautics and Space Administration) p1
[2] 汪志诚 2013 热力学·统计物理 (第五版) (北京: 高等教育出版社) 第1页
Wang Z C 2013 Thermodynamic·statistical physics (Vol. 5) (Beijing: Higher Education Press) p1 (in Chinese)
[3] Gabriel V O, Luis A A H 2018 Int. J. Quantum Chem. 118 1
Google Scholar
[4] Irwin A W 1988 Astron. Astrophys. Suppl. Ser. 74 145
[5] Fischer J, Gamache R R, Goldman A, Rothman L S, Perrin A 2003 J. Quant. Spectrosc. Radiat. Transfer 82 401
Google Scholar
[6] 伍冬兰, 万慧军, 谢安东, 程新路, 杨向东 2009 58 7410
Google Scholar
Wu D L, Wan H J, Xie A D, Cheng X L, Yang X D 2009 Acta Phys. Sin. 58 7410
Google Scholar
[7] Jia C S, Zhang L H, Wang C W 2017 Chem. Phys. Lett. 667 211
Google Scholar
[8] Maltsev M A, Kulikov A N, Morozov I V 2016 J. Phys. Conf. Ser. 774 012023
Google Scholar
[9] Maltsev M A, Morozov I V, Osina E L 2019 High Temp. 57 335
Google Scholar
[10] Ikot A N, Chukwuocha E O, Onyeaju M C, Onate C A, Ita B I, Udoh M E 2018 Pramana-J. Phys. 90 22
Google Scholar
[11] 王小霞, 刘鑫, 张琼, 陈宏善 2017 66 103601
Google Scholar
Wang X X, Liu X, Zhang Q, Chen H S 2017 Acta Phys. Sin. 66 103601
Google Scholar
[12] Maltsev M A, Morozov I V, Osina E L 2019 High Temp. 57 42
Google Scholar
[13] Horchani R, Jelassi H 2020 Chem. Phys. 532 1
Google Scholar
[14] Zúñiga J, Bastida A, Requena A, Cerezo J 2021 J. Phys. Chem. A 125 9226
Google Scholar
[15] Sun W G, Hou S L, Feng H, Ren W Y 2002 J. Mol. Spectrosc. 215 93
Google Scholar
[16] Fu J, Fan Q C, Liu G Y, Li H D, Xu Y G, Fan Z X, Zhang Y 2017 Comput. Theor. Chem. 1115 136
Google Scholar
[17] McDowell R S 1988 J. Chem. Phys. 88 356
Google Scholar
[18] 蹇君, 雷娇, 樊群超, 范志祥, 马杰, 付佳, 李会东, 徐勇根 2020 69 053301
Google Scholar
Jian J, Lei J, Fan Q C, Fan Z X, Ma J, Fu J, Li H D, Xu Y G 2020 Acta Phys. Sin. 69 053301
Google Scholar
[19] Rydberg R 1932 Z. Phys. 73 376
Google Scholar
[20] Klein V O 1932 Z. Phys. 76 226
Google Scholar
[21] Rees A L G 1947 Proc. Phys. Soc. 59 998
Google Scholar
[22] Pathria R K 1977 Statistical Mechanics (London: Pcrgamon Press) p100
[23] Le Roy R J 2017 J. Quant. Spectrosc. Radiat. Transfer 186 167
Google Scholar
[24] Li C L, Li Y C, Ji Z H, Qiu X B, Lai Y Z, Wei J L, Zhao Y T, Deng L H, Chen Y Q, Liu J J 2018 Phys. Rev. A 97 062501
Google Scholar
[25] Laurendeau N M 2005 Statistical Thermodynamics: Fundamentals and Applications (England: Cambridge University Press) p1
[26] Huang K 1965 Phys. Today 18 92
[27] Babou Y, Rivière P, Perrin M Y, Soufiani A 2009 Int. J. Thermophys. 30 416
Google Scholar
[28] Jaffe R L 1987 AIAA 22nd Thermophysics Conference (New York: American Institute of Aeronautics and Astronautics) p1633
[29] Capitelli M, Colonna G, Giordano D, Maraffa L, Casavola A, Minelli P, Pagano D, Pietanza L D, Taccogna F 2005 Tables of Internal Partition Functions and Thermodynamic Properties of High-Temperature Mars-Atmosphere Species from 50 K to 50000 K (Netherlands: European Space Agency Publications Division) p3
[30] Huber K P, Herzberg G 1950 Molecular Spectra and Molecular Structure: Spectra of Diatomic Molecules (New York: Van Nostrand Reinhold Company) p9
[31] 朱华, 谢代前, 鄢国森 1999 高等学校化学学报 20 1910
Google Scholar
Zhu H, Xie D Q, Yan G S 1999 Chem. J. Chin. Univ. 20 1910
Google Scholar
[32] James B B, Edward R L, Philip D H, Carleton J H 1987 J. Mol. Spectrosc. 124 379
Google Scholar
[33] Gottlieb C A, Gottlieb E W, Litvak M M, Ball J A, Penfield H 1978 Astrophys. J. 219 77
Google Scholar
[34] Clyne M A A, Mcdermid I S 1979 J. Chem. Soc. , Faraday Trans. 2 75 905
Google Scholar
[35] Peterson K A, Woods R C 1990 J. Chem. Phys. 93 1876
Google Scholar
[36] Martin-Drumel M A, Hindle F, Mouret G, Cuisset A, Cernicharo J 2015 Astrophys. J. 799 115
Google Scholar
[37] Chase M W 1998 Journal of Physical and Chemical Reference DataMonograph (Vol. 9) (New York: National Institute of Standards and Technology Gaithersburg) p1726
-
图 1 基于VAM和RKR方法构建的势能曲线与实验势能曲线的对比
Figure 1. Comparisons of the potential energy curves constructed based on the VAM and RKR method with those experimentally.
图 2 不同摩尔热容误差的比较
Figure 2. Comparisons of the errors of different molar heat capacities.
表 1 不同方法所得SO分子电子基态的振动光谱常数 (单位: cm–1)
Table 1. Vibrational spectral constants of SO in the ground electronic state obtained by different methods (in cm–1)
$ {\omega _0} $ $ {\omega _{\text{e}}} $ $ {\omega _{\text{e}}}{x_{\text{e}}} $ $ {\omega _{\text{e}}}{y_{\text{e}}} $ $ {\omega _{\text{e}}}{z_{\text{e}}} $ $ {\omega _{\text{e}}}{t_{\text{e}}} $ 实验[34] 1148.19 6.12 CASS-
CF[35]1161.80 6.50 CI-SD[35] 1263.50 5.35 MP4
SDQ[35]1173.10 5.09 VAM 0.75 1147.71 5.99 –1.55×10–2 7.59×10–4 –1.30×10–5 
DownLoad: CSV
表 2 不同摩尔热容与实验值的误差 (单位: J·mol–1·K–1)
Table 2. Errors between different molar heat capacities and observed experimentally (in J·mol–1·K–1)
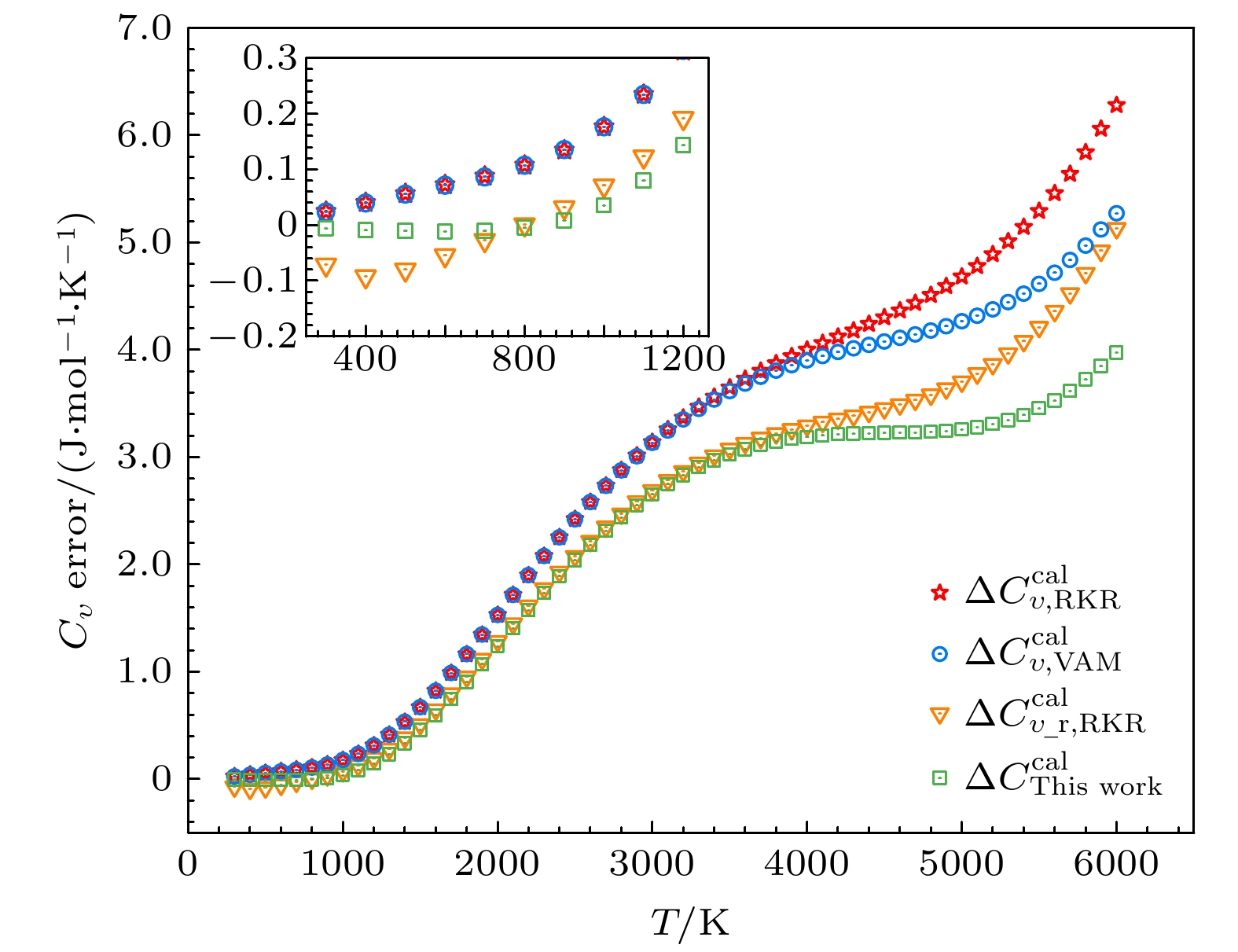
T/K ${ C_\upsilon ^{ {\text{expt} } } }^{\rm\; a}$ ${ \Delta C_{\upsilon {\text{, RKR} } }^{ {\text{cal} } } } ^{\rm\; b}$ ${ \Delta C_{\upsilon {\text{, VAM} } }^{ {\text{cal} } } }^{\rm\; c}$ ${ \Delta C_{\upsilon \_r{\text{, RKR} } }^{ {\text{cal} } } } ^{\rm\; d}$ ${ \Delta C_{ {\text{This work} } }^{ {\text{cal} } } }^{\rm\; e}$ 300 30.197 –0.025 –0.024 0.071 0.006 400 31.560 –0.041 –0.040 0.092 0.009 500 32.826 –0.057 –0.056 0.080 0.011 600 33.838 –0.073 –0.072 0.054 0.011 700 34.612 –0.088 –0.087 0.027 0.011 800 35.206 –0.108 –0.108 –0.001 0.005 900 35.672 –0.135 –0.136 –0.032 –0.008 1000 36.053 –0.177 –0.177 –0.071 –0.035 1100 36.379 –0.235 –0.235 –0.123 –0.079 1200 36.672 –0.313 –0.314 –0.192 –0.143 1300 36.946 –0.412 –0.413 –0.280 –0.228 1400 37.210 –0.532 –0.533 –0.386 –0.333 1500 37.469 –0.670 –0.670 –0.508 –0.455 1600 37.725 –0.822 –0.823 –0.645 –0.593 1700 37.980 –0.989 –0.989 –0.795 –0.743 1800 38.232 –1.163 –1.164 –0.952 –0.902 1900 38.482 –1.345 –1.346 –1.116 –1.068 2000 38.727 –1.530 –1.530 –1.282 –1.236 2100 38.967 –1.715 –1.716 –1.449 –1.404 2200 39.200 –1.899 –1.900 –1.614 –1.571 2300 39.425 –2.079 –2.079 –1.775 –1.733 2400 39.641 –2.254 –2.254 –1.929 –1.889 2500 39.847 –2.422 –2.421 –2.077 –2.038 2600 40.043 –2.582 –2.581 –2.217 –2.180 2700 40.229 –2.735 –2.733 –2.349 –2.313 2800 40.404 –2.879 –2.876 –2.472 –2.436 2900 40.568 –3.014 –3.009 –2.585 –2.549 3000 40.721 –3.140 –3.133 –2.689 –2.652 3100 40.864 –3.258 –3.248 –2.784 –2.746 3200 40.996 –3.367 –3.352 –2.869 –2.830 3300 41.119 –3.469 –3.449 –2.946 –2.904 3400 41.232 –3.562 –3.536 –3.015 –2.969 3500 41.336 –3.649 –3.615 –3.076 –3.025 3600 41.432 –3.729 –3.686 –3.130 –3.072 3700 41.520 –3.804 –3.749 –3.178 –3.111 3800 41.601 –3.874 –3.806 –3.220 –3.143 3900 41.676 –3.940 –3.857 –3.259 –3.168 4000 41.745 –4.002 –3.902 –3.293 –3.187 4100 41.810 –4.063 –3.943 –3.326 –3.202 4200 41.871 –4.122 –3.980 –3.356 –3.211 4300 41.929 –4.180 –4.014 –3.387 –3.217 4400 41.986 –4.241 –4.047 –3.419 –3.221 4500 42.042 –4.303 –4.079 –3.453 –3.224 4600 42.098 –4.367 –4.111 –3.490 –3.226 4700 42.156 –4.437 –4.144 –3.533 –3.229 4800 42.217 –4.512 –4.181 –3.581 –3.235 4900 42.282 –4.593 –4.221 –3.637 –3.244 5000 42.352 –4.682 –4.266 –3.702 –3.258 5100 42.429 –4.781 –4.318 –3.778 –3.279 5200 42.514 –4.891 –4.377 –3.865 –3.307 5300 42.608 –5.012 –4.445 –3.966 –3.344 5400 42.712 –5.146 –4.523 –4.080 –3.392 5500 42.829 –5.295 –4.614 –4.211 –3.453 5600 42.959 –5.459 –4.718 –4.359 –3.527 5700 43.104 –5.641 –4.837 –4.526 –3.617 5800 43.265 –5.841 –4.971 –4.714 –3.724 5900 43.444 –6.061 –5.123 –4.923 –3.849 6000 43.620 –6.280 –5.273 –5.133 –3.973 $ \Delta {C_{{\text{aver}}}} $f 2.896 2.721 2.363 2.084 注: a. 实验热容; b. 基于实验振动能级运用近似模型所得热容值与实验值的误差; c. 基于VAM完全振动能级运用近似模型所得热容值与实验值的误差; d. 基于实验振转能级所得热容值与实验值的误差; e. 基于完全振转能级所得热容值与实验值的误差; f. $\Delta {C_{ {\text{aver} } } } = \dfrac{ {\text{1} } }{w} \displaystyle\sum {\left| { {C_{\text{m} } } - {C_{ {\text{expt} } } } } \right|}$, w为参与计算的热容值个数.
DownLoad: CSV
-
[1] McBride B J, Zehe M J, Gordon S 2002 NASA Glenn Coefficients for Calculating Thermodynamic Properties of Individual Species (Cleveland: National Aeronautics and Space Administration) p1
[2] 汪志诚 2013 热力学·统计物理 (第五版) (北京: 高等教育出版社) 第1页
Wang Z C 2013 Thermodynamic·statistical physics (Vol. 5) (Beijing: Higher Education Press) p1 (in Chinese)
[3] Gabriel V O, Luis A A H 2018 Int. J. Quantum Chem. 118 1
Google Scholar
[4] Irwin A W 1988 Astron. Astrophys. Suppl. Ser. 74 145
[5] Fischer J, Gamache R R, Goldman A, Rothman L S, Perrin A 2003 J. Quant. Spectrosc. Radiat. Transfer 82 401
Google Scholar
[6] 伍冬兰, 万慧军, 谢安东, 程新路, 杨向东 2009 58 7410
Google Scholar
Wu D L, Wan H J, Xie A D, Cheng X L, Yang X D 2009 Acta Phys. Sin. 58 7410
Google Scholar
[7] Jia C S, Zhang L H, Wang C W 2017 Chem. Phys. Lett. 667 211
Google Scholar
[8] Maltsev M A, Kulikov A N, Morozov I V 2016 J. Phys. Conf. Ser. 774 012023
Google Scholar
[9] Maltsev M A, Morozov I V, Osina E L 2019 High Temp. 57 335
Google Scholar
[10] Ikot A N, Chukwuocha E O, Onyeaju M C, Onate C A, Ita B I, Udoh M E 2018 Pramana-J. Phys. 90 22
Google Scholar
[11] 王小霞, 刘鑫, 张琼, 陈宏善 2017 66 103601
Google Scholar
Wang X X, Liu X, Zhang Q, Chen H S 2017 Acta Phys. Sin. 66 103601
Google Scholar
[12] Maltsev M A, Morozov I V, Osina E L 2019 High Temp. 57 42
Google Scholar
[13] Horchani R, Jelassi H 2020 Chem. Phys. 532 1
Google Scholar
[14] Zúñiga J, Bastida A, Requena A, Cerezo J 2021 J. Phys. Chem. A 125 9226
Google Scholar
[15] Sun W G, Hou S L, Feng H, Ren W Y 2002 J. Mol. Spectrosc. 215 93
Google Scholar
[16] Fu J, Fan Q C, Liu G Y, Li H D, Xu Y G, Fan Z X, Zhang Y 2017 Comput. Theor. Chem. 1115 136
Google Scholar
[17] McDowell R S 1988 J. Chem. Phys. 88 356
Google Scholar
[18] 蹇君, 雷娇, 樊群超, 范志祥, 马杰, 付佳, 李会东, 徐勇根 2020 69 053301
Google Scholar
Jian J, Lei J, Fan Q C, Fan Z X, Ma J, Fu J, Li H D, Xu Y G 2020 Acta Phys. Sin. 69 053301
Google Scholar
[19] Rydberg R 1932 Z. Phys. 73 376
Google Scholar
[20] Klein V O 1932 Z. Phys. 76 226
Google Scholar
[21] Rees A L G 1947 Proc. Phys. Soc. 59 998
Google Scholar
[22] Pathria R K 1977 Statistical Mechanics (London: Pcrgamon Press) p100
[23] Le Roy R J 2017 J. Quant. Spectrosc. Radiat. Transfer 186 167
Google Scholar
[24] Li C L, Li Y C, Ji Z H, Qiu X B, Lai Y Z, Wei J L, Zhao Y T, Deng L H, Chen Y Q, Liu J J 2018 Phys. Rev. A 97 062501
Google Scholar
[25] Laurendeau N M 2005 Statistical Thermodynamics: Fundamentals and Applications (England: Cambridge University Press) p1
[26] Huang K 1965 Phys. Today 18 92
[27] Babou Y, Rivière P, Perrin M Y, Soufiani A 2009 Int. J. Thermophys. 30 416
Google Scholar
[28] Jaffe R L 1987 AIAA 22nd Thermophysics Conference (New York: American Institute of Aeronautics and Astronautics) p1633
[29] Capitelli M, Colonna G, Giordano D, Maraffa L, Casavola A, Minelli P, Pagano D, Pietanza L D, Taccogna F 2005 Tables of Internal Partition Functions and Thermodynamic Properties of High-Temperature Mars-Atmosphere Species from 50 K to 50000 K (Netherlands: European Space Agency Publications Division) p3
[30] Huber K P, Herzberg G 1950 Molecular Spectra and Molecular Structure: Spectra of Diatomic Molecules (New York: Van Nostrand Reinhold Company) p9
[31] 朱华, 谢代前, 鄢国森 1999 高等学校化学学报 20 1910
Google Scholar
Zhu H, Xie D Q, Yan G S 1999 Chem. J. Chin. Univ. 20 1910
Google Scholar
[32] James B B, Edward R L, Philip D H, Carleton J H 1987 J. Mol. Spectrosc. 124 379
Google Scholar
[33] Gottlieb C A, Gottlieb E W, Litvak M M, Ball J A, Penfield H 1978 Astrophys. J. 219 77
Google Scholar
[34] Clyne M A A, Mcdermid I S 1979 J. Chem. Soc. , Faraday Trans. 2 75 905
Google Scholar
[35] Peterson K A, Woods R C 1990 J. Chem. Phys. 93 1876
Google Scholar
[36] Martin-Drumel M A, Hindle F, Mouret G, Cuisset A, Cernicharo J 2015 Astrophys. J. 799 115
Google Scholar
[37] Chase M W 1998 Journal of Physical and Chemical Reference DataMonograph (Vol. 9) (New York: National Institute of Standards and Technology Gaithersburg) p1726
DownLoad:
Catalog
Metrics
- Abstract views: 3553
- PDF Downloads: 41
- Cited By: 0
