Stochastic resonance in periodic potential system with memory damping function

Xu Peng-Fei; Gong Xu-Lu; Li Yi-Wei; Jin Yan-Fei

doi:10.7498/aps.71.20211732

Abstract

The stochastic dynamical system with memory effects describes a non-Markovian process that can happen in some complex systems or disordered media, such as viscoelastic media and living cell. Its velocity yields the memory effects because of the nonlocality in time, giving rise to a generalized Langevin equation for describing the dynamics of the system. In particular, the friction term in generalized Langevin equation is given by the time-dependent memory kernel. Besides, the research of stochastic resonance in periodic potential models emerges as an important subject because such systems have potential applications in diverse areas of natural sciences. However, the analysis of the influence of memory on stochastic resonance has not been reported so far in periodic potential model. In this paper, the phenomenon of stochastic resonance is investigated in the periodic potential system with friction memory kernel driven by an external periodic signal and internal noise. The generalized Langevin equation is converted into the three-dimensional Markovian Langevin equations. Analytical expression for the spectral amplification, together with the amplitude of the response, is derived in the periodic potential with an arbitrary number of simultaneously stable steady states, which can be applied to the general multi-stable dynamical model. The obtained results indicate that the curve of spectral amplification versus temperature exhibits a pronounced peak. Obviously, this typical phenomenon is a signature of stochastic resonance. The stochastic resonance effect is enhanced with the increase of the memory time or the number of stable steady states. For a certain range of the particle motion, the existence of an optimal number of stable steady states for which the output of the system can be maximized is established. Moreover, the phenomenon of stochastic resonance is studied according to the stochastic energetics. The average input energy per period is calculated over all the trajectories for quantifying stochastic resonance. It is found that the stochastic resonance effect is first weakened and then enhanced with increasing memory time. Specifically, under appropriate temperature conditions, there is an optimal memory time, which can maximize the work done by the external periodic force on the system.

Keywords:

Authors and contacts

1.
Department of Mathematics, Shanxi Agricultural University, Taigu 030801, China
2.
School of Software, Shanxi Agricultural University, Taigu 030801, China
3.
Department of Mechanics, Beijing Institute of Technology, Beijing 100081, China

Corresponding author: Jin Yan-Fei, jinyf@bit.edu.cn

Funds: Project supported by the Excellent Talents Coming to Shanxi Reward Scientific Research Project, China (Grant No. SXBYKY2021081), the Starting Foundation of Scientific Research for the Doctor of Shanxi Agricultural University, China (Grant No. 2021BQ12), the Science and Technology Innovation Foundation for Young Scientists of Shanxi Agricultural University, China (Grant Nos. 2019019, 2020QC04), and the Teaching Reform Project for Postgraduate of Beijing Institute of Technology, China.

FullText HTML : translate this paragraph

References

[1]	Benzi R, Sutera A, Vulpiani A 1981 J. Phys. A 14 L453 Google Scholar
[2]	Gammaitoni L, Hänggi P, Jung P, Marchesoni F 1998 Rev. Mod. Phys. 70 223 Google Scholar
[3]	Nicolis C 2010 Phys. Rev. E 82 011139 Google Scholar
[4]	Qiao Z J, Lei Y G, Li N P 2019 Mech. Syst. Sig. Process. 122 502 Google Scholar
[5]	Goychuk I, Pöschel T 2020 New J. Phys. 22 113018 Google Scholar
[6]	Mokshin A V, Yulmetyev R M, Hänggi P 2005 Phys. Rev. Lett. 95 200601 Google Scholar
[7]	Despósito M A, Pallavicini C, Levi V, Bruno L 2011 Physica A 390 1026 Google Scholar
[8]	Tolić-Nørrelykke I M, Munteanu E L, Thon G, Oddershede L, Berg-Sørensen K 2004 Phys. Rev. Lett. 93 078102 Google Scholar
[9]	Viñales A D, Despósito M A 2006 Phys. Rev. E 73 016111 Google Scholar
[10]	Bao J D, Zhuo Y Z 2003 Phys. Rev. Lett. 91 138104 Google Scholar
[11]	Goychuk I 2010 Chem. Phys. 375 450 Google Scholar
[12]	Wang K G, Masoliver J 1996 Physica A 231 615 Google Scholar
[13]	Xu P F, Jin Y F 2020 Chaos, Solitons & Fractals 138 109857 Google Scholar
[14]	Kumar N 2012 Phys. Rev. E 85 011114 Google Scholar
[15]	Kubo R, Toda M, Hashitsume N 1985 Statistical Physics II: Non-equilibrium Statistical Mechanics (Berlin: Springer-Verlag) p31
[16]	Goswami G, Mukherjee B, Bag B C 2005 Chem. Phys. 312 47 Google Scholar
[17]	Hohenegger C, Durr R, Senter D M 2017 J. Non-Newton. Fluid 242 48 Google Scholar
[18]	Zhong S C, Zhang L, Wang H Q, Ma H, Luo M K 2017 Nonlinear Dyn. 89 1327 Google Scholar
[19]	谢文贤, 李东平, 许鹏飞, 蔡力, 靳艳飞 2014 63 100502 Google Scholar Xie W X, Li D P, Xu P F, Cai L, Jin Y F 2014 Acta Phys. Sin. 63 100502 Google Scholar
[20]	He G T, Guo D L, Tian Y, Li T J, Luo M K 2017 Physica A 484 91 Google Scholar
[21]	Hasegawa H 2013 Physica A 392 2532 Google Scholar
[22]	Srokowski T 2013 Eur. Phys. J. B 86 239 Google Scholar
[23]	Coffey W T, Kalmykov Y P, Massawe E S 1993 Phys. Rev. E 48 77 Google Scholar
[24]	Elston T C, Peskin C S 2000 SIAM J. Appl. Math. 60 842 Google Scholar
[25]	Hänggi P, Bartussek R, Talkner P, Łuczka J 1996 Europhys. Lett. 35 315 Google Scholar
[26]	Reenbohn W L, Mahato M C 2015 Phys. Rev. E 91 052151 Google Scholar
[27]	Li J H 2010 J. Phys. Condens. Mater. 22 115702 Google Scholar
[28]	Jin Y F, Ma Z M, Xiao S M 2017 Chaos, Solitons & Fractals 103 470 Google Scholar
[29]	Saikia S 2014 Physica A 416 411 Google Scholar
[30]	Reenbohn W L, Pohlong S S, Mahato M C 2012 Phys. Rev. E 85 031144 Google Scholar
[31]	谢勇, 刘若男 2017 66 120501 Google Scholar Xie Y, Liu R N 2017 Acta Phys. Sin. 66 120501 Google Scholar
[32]	Sawkmie I S, Mahato M C 2019 Commun. Nonlinear Sci. Numer. Simul. 78 104859 Google Scholar
[33]	Liu R N, Kang Y M 2018 Phys. Lett. A 382 1656 Google Scholar
[34]	Liu K H, Jin Y F 2013 Physica A 392 5283 Google Scholar
[35]	Neiman A, Sung W 1996 Phys. Lett. A 223 341 Google Scholar
[36]	Bao J D, Bai Z W 2005 Chin. Phys. Lett. 22 1845 Google Scholar
[37]	康艳梅, 徐健学, 谢勇 2003 52 802 Google Scholar Kang Y M, Xu J X, Xie Y 2003 Acta Phys. Sin. 52 802 Google Scholar
[38]	Nicolis C 2012 Phys. Rev. E 86 011133 Google Scholar
[39]	Dykman M I, Haken H, Hu G, Luchinsky D G, Mannella R, Mcclintock P V E, Ning C Z, Stein N D, Stocks N G 1993 Phys. Lett. A 180 332 Google Scholar
[40]	Jin Y F 2012 Physica A 391 1928 Google Scholar

Cited By

图 1 (a)周期势函数; (b)离散的多稳态过程

Figure 1. (a) Periodic potential; (b) discrete multi-stable process.

DownLoad: Full-Size Img PowerPoint

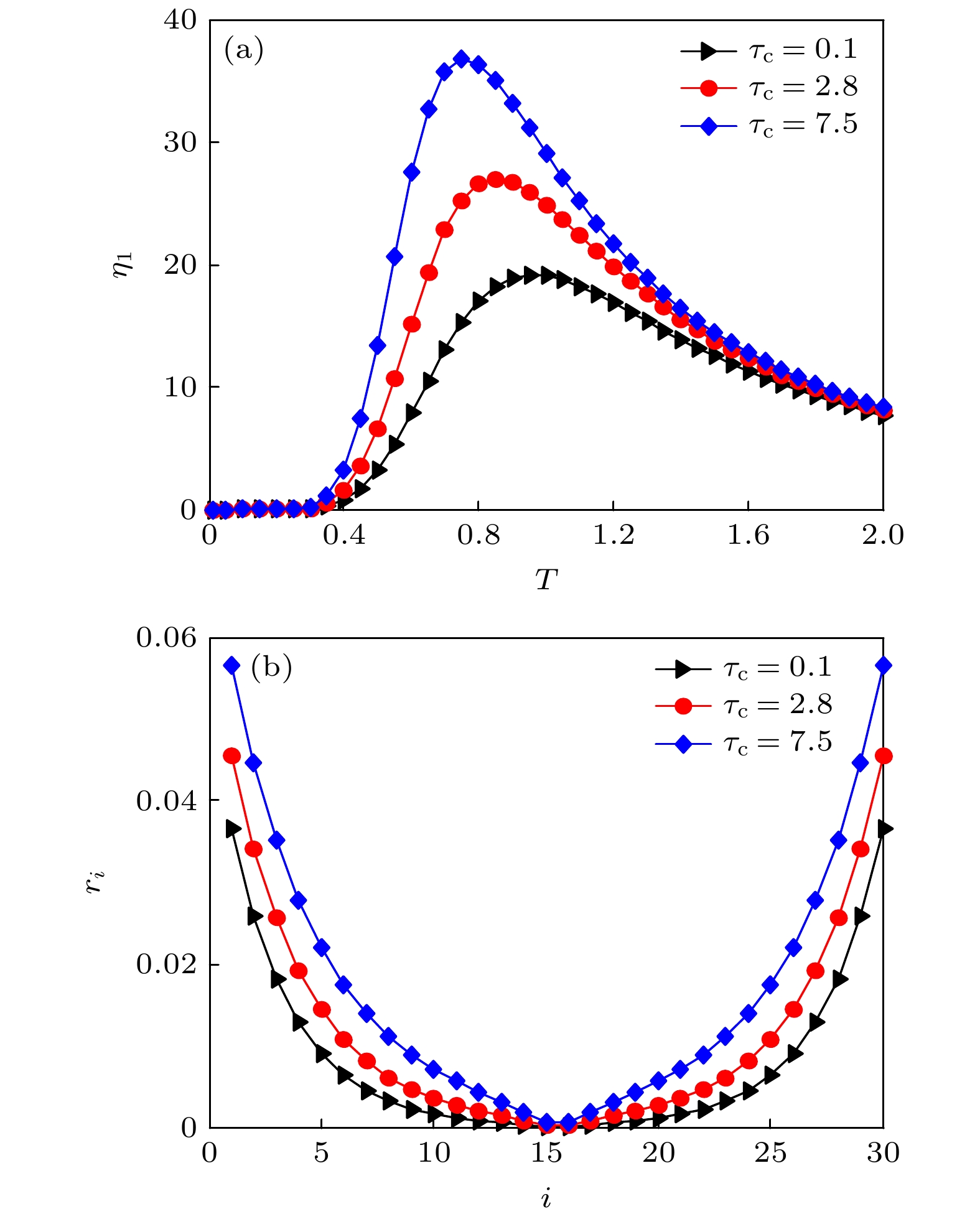
图 2 记忆时间$ {\tau _c} $对随机共振的影响　(a) 功率谱放大因子$ {\eta _1} $随温度T的变化曲线($ n = 6 $); (b)第i个稳态点对应的响应振幅$ {r_i} $的变化曲线. 其他参数取值为$\varGamma = 4$, ${\gamma _0} = $$ 1$, $ \omega = 0.001 $和$ {m_0} = 1 $

Figure 2. The effects of memory time $ {\tau _c} $ on stochastic resonance: (a) Spectral amplification $ {\eta _1} $versus temperature T; (b) amplitude of the response $ {r_i} $ versus i. Other parameter values are chosen as $\varGamma = 4$, $ {\gamma _0} = 1 $, $ \omega = 0.001 $ and $ {m_0} = 1 $.

DownLoad: Full-Size Img PowerPoint

图 3 功率谱密度(PSD)作为频率的函数曲线　(a)不同的温度T和$ {\tau _c} = 1 $; (b)不同的记忆时间$ {\tau _c} $和$ T = 0.75 $. 其他参数取值为$\varGamma = 4$, $ {\gamma _0} = 1 $, $ {\varepsilon _0} = 0.3 $, $ \omega = 0.001 $和$ {m_0} = 1 $

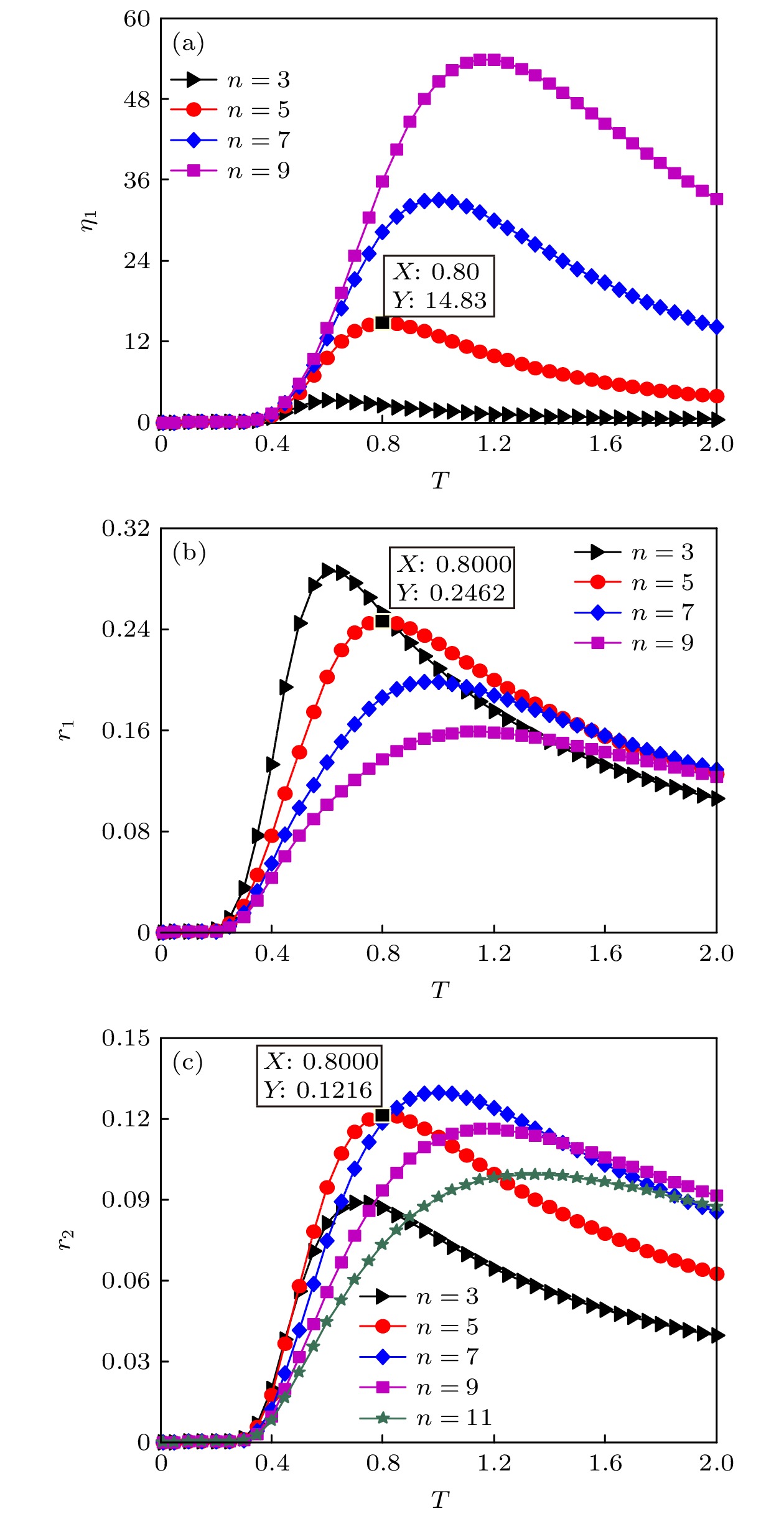
Figure 3. Power spectrum density (PSD) of the system as a function of frequency with different values of (a) temperature T ($ {\tau _c} = 1 $); (b) memory time $ {\tau _c} $ ($ T = 0.75 $). Other parameter values are chosen as $\varGamma = 4$, $ {\gamma _0} = 1 $, $ {\varepsilon _0} = 0.3 $, $ \omega = 0.001 $ and $ {m_0} = 1 $.

DownLoad: Full-Size Img PowerPoint

图 4 稳态点个数n对随机共振的影响　(a)功率谱放大因子$ {\eta _1} $随温度T的变化曲线; (b)响应振幅$ {r_1} $随T的变化曲线; (c)响应振幅$ {r_2} $随T的变化曲线. 其他参数取值为$ {\tau _c} = 3 $, $\varGamma = 5$, $ {\gamma _0} = 1 $, $ \omega = 0.001 $和$ {m_0} = 1 $

Figure 4. The effects of the number of stable steady states n on stochastic resonance: (a) Spectral amplification $ {\eta _1} $ versus temperature T; (b) amplitude of the response $ {r_1} $ versus T; (c) amplitude of the response $ {r_2} $ versus T. Other parameter values are chosen as $ {\tau _c} = 3 $, $\varGamma = 5$, $ {\gamma _0} = 1 $, $ \omega = 0.001 $ and $ {m_0} = 1 $.

DownLoad: Full-Size Img PowerPoint

图 5 功率谱放大因子$ {\eta _1} $作为区间内稳态点个数n的函数曲线　(a)不同的区间长度L和$\varGamma = 3$; (b)不同的记忆强度Γ和固定的长度$ L = 10 $. 其他参数取值为$ {\tau _c} = 4 $, ${\gamma _0} = $$ 1$, $ \omega = 0.002 $和$ T = 0.8 $

Figure 5. Spectral amplification $ {\eta _1} $ versus the number of stable steady states n with different values of (a) interval length L ($\varGamma = 3$) and (b) memory strength Γ ($ L = 10 $). Other parameter values are chosen as $ {\tau _c} = 4 $, $ {\gamma _0} = 1 $, $ \omega = 0.002 $ and $ T = 0.8 $.

DownLoad: Full-Size Img PowerPoint

图 6 平均输入能量$ \overline W $作为初始位置$ x(0) $的函数随不同温度T的变化情况, 黑色线代表系统的输入信号$ {\varepsilon _0}\cos (\omega t) $　(a) T = 0.001; (b) T = 0.003; (c) T = 0.009; (d) T = 0.018. 其他参数取值为$ {\tau _c} = 2.3 $, $ {\gamma _0} = 0.12 $, $\varGamma = 0.02$和$ \omega = {\pi {\left/ {\vphantom {\pi 4}} \right.} 4} $

Figure 6. Average input energy $ \overline W $ averaged over an entire trajectory with initial position $ x(0) $ for different values of temperature T, where the black line denotes the input signal $ {\varepsilon _0}\cos (\omega t) $: (a) T = 0.001; (b) T = 0.003; (c) T = 0.009; (d) T = 0.018. Other parameter values are chosen as $ {\tau _c} = 2.3 $, $ {\gamma _0} = 0.12 $, $\varGamma = 0.02$ and $ \omega = {\pi {\left/ {\vphantom {\pi 4}} \right. } 4} $.

DownLoad: Full-Size Img PowerPoint

图 7 记忆强度Γ对输入能量的影响　(a)平均输入能量$ \left\langle {\overline W } \right\rangle $随温度T的变化曲线; (b)相位差$\overline \varPhi$随T的变化曲线. 其他参数取值为$ {\tau _c} = 2.3 $, $ {\gamma _0} = 0.12 $和$ \omega = {\pi {\left/ {\vphantom {\pi 4}} \right. } 4} $

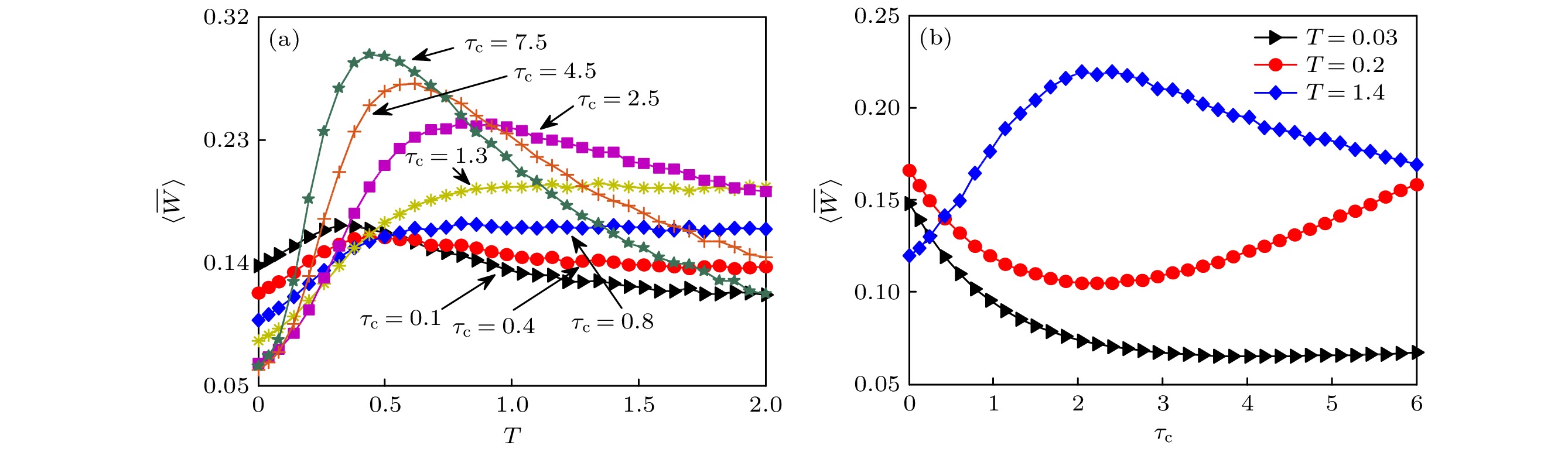
Figure 7. The effects of memory strength Γ on input energy: (a) Average input energy $ \left\langle {\overline W } \right\rangle $ versus temperature T; (b) phase lag $\overline \varPhi$ versus T. Other parameter values are chosen as $ {\tau _c} = 2.3 $, $ {\gamma _0} = 0.12 $ and $ \omega = {\pi {\left/ {\vphantom {\pi 4}} \right. } 4} $.

DownLoad: Full-Size Img PowerPoint

图 8 记忆时间$ {\tau _c} $对输入能量的影响　(a)$ \left\langle {\overline W } \right\rangle $随T的变化曲线; (b)$ \left\langle {\overline W } \right\rangle $随$ {\tau _c} $的变化曲线. 其他参数取值为$ \varGamma = 0.7 $, $ {\gamma _0} = 0.12 $和$ \omega = {\pi {\left/ {\vphantom {\pi 4}} \right. } 4} $

Figure 8. The effects of memory time $ {\tau _{\rm{c}}} $ on input energy: (a) $ \left\langle {\overline W } \right\rangle $ versus T; (b) $ \left\langle {\overline W } \right\rangle $ versus $ {\tau _c} $. Other parameter values are chosen as $\varGamma = 0.7$, $ {\gamma _0} = 0.12 $ and $ \omega = {\pi {\left/ {\vphantom {\pi 4}} \right. } 4} $.

DownLoad: Full-Size Img PowerPoint

map

[1]	Benzi R, Sutera A, Vulpiani A 1981 J. Phys. A 14 L453 Google Scholar
[2]	Gammaitoni L, Hänggi P, Jung P, Marchesoni F 1998 Rev. Mod. Phys. 70 223 Google Scholar
[3]	Nicolis C 2010 Phys. Rev. E 82 011139 Google Scholar
[4]	Qiao Z J, Lei Y G, Li N P 2019 Mech. Syst. Sig. Process. 122 502 Google Scholar
[5]	Goychuk I, Pöschel T 2020 New J. Phys. 22 113018 Google Scholar
[6]	Mokshin A V, Yulmetyev R M, Hänggi P 2005 Phys. Rev. Lett. 95 200601 Google Scholar
[7]	Despósito M A, Pallavicini C, Levi V, Bruno L 2011 Physica A 390 1026 Google Scholar
[8]	Tolić-Nørrelykke I M, Munteanu E L, Thon G, Oddershede L, Berg-Sørensen K 2004 Phys. Rev. Lett. 93 078102 Google Scholar
[9]	Viñales A D, Despósito M A 2006 Phys. Rev. E 73 016111 Google Scholar
[10]	Bao J D, Zhuo Y Z 2003 Phys. Rev. Lett. 91 138104 Google Scholar
[11]	Goychuk I 2010 Chem. Phys. 375 450 Google Scholar
[12]	Wang K G, Masoliver J 1996 Physica A 231 615 Google Scholar
[13]	Xu P F, Jin Y F 2020 Chaos, Solitons & Fractals 138 109857 Google Scholar
[14]	Kumar N 2012 Phys. Rev. E 85 011114 Google Scholar
[15]	Kubo R, Toda M, Hashitsume N 1985 Statistical Physics II: Non-equilibrium Statistical Mechanics (Berlin: Springer-Verlag) p31
[16]	Goswami G, Mukherjee B, Bag B C 2005 Chem. Phys. 312 47 Google Scholar
[17]	Hohenegger C, Durr R, Senter D M 2017 J. Non-Newton. Fluid 242 48 Google Scholar
[18]	Zhong S C, Zhang L, Wang H Q, Ma H, Luo M K 2017 Nonlinear Dyn. 89 1327 Google Scholar
[19]	谢文贤, 李东平, 许鹏飞, 蔡力, 靳艳飞 2014 63 100502 Google Scholar Xie W X, Li D P, Xu P F, Cai L, Jin Y F 2014 Acta Phys. Sin. 63 100502 Google Scholar
[20]	He G T, Guo D L, Tian Y, Li T J, Luo M K 2017 Physica A 484 91 Google Scholar
[21]	Hasegawa H 2013 Physica A 392 2532 Google Scholar
[22]	Srokowski T 2013 Eur. Phys. J. B 86 239 Google Scholar
[23]	Coffey W T, Kalmykov Y P, Massawe E S 1993 Phys. Rev. E 48 77 Google Scholar
[24]	Elston T C, Peskin C S 2000 SIAM J. Appl. Math. 60 842 Google Scholar
[25]	Hänggi P, Bartussek R, Talkner P, Łuczka J 1996 Europhys. Lett. 35 315 Google Scholar
[26]	Reenbohn W L, Mahato M C 2015 Phys. Rev. E 91 052151 Google Scholar
[27]	Li J H 2010 J. Phys. Condens. Mater. 22 115702 Google Scholar
[28]	Jin Y F, Ma Z M, Xiao S M 2017 Chaos, Solitons & Fractals 103 470 Google Scholar
[29]	Saikia S 2014 Physica A 416 411 Google Scholar
[30]	Reenbohn W L, Pohlong S S, Mahato M C 2012 Phys. Rev. E 85 031144 Google Scholar
[31]	谢勇, 刘若男 2017 66 120501 Google Scholar Xie Y, Liu R N 2017 Acta Phys. Sin. 66 120501 Google Scholar
[32]	Sawkmie I S, Mahato M C 2019 Commun. Nonlinear Sci. Numer. Simul. 78 104859 Google Scholar
[33]	Liu R N, Kang Y M 2018 Phys. Lett. A 382 1656 Google Scholar
[34]	Liu K H, Jin Y F 2013 Physica A 392 5283 Google Scholar
[35]	Neiman A, Sung W 1996 Phys. Lett. A 223 341 Google Scholar
[36]	Bao J D, Bai Z W 2005 Chin. Phys. Lett. 22 1845 Google Scholar
[37]	康艳梅, 徐健学, 谢勇 2003 52 802 Google Scholar Kang Y M, Xu J X, Xie Y 2003 Acta Phys. Sin. 52 802 Google Scholar
[38]	Nicolis C 2012 Phys. Rev. E 86 011133 Google Scholar
[39]	Dykman M I, Haken H, Hu G, Luchinsky D G, Mannella R, Mcclintock P V E, Ning C Z, Stein N D, Stocks N G 1993 Phys. Lett. A 180 332 Google Scholar
[40]	Jin Y F 2012 Physica A 391 1928 Google Scholar

[1]	Xie Yong, Liu Ruo-Nan. Stochastic resonance in overdamped washboard potential system. Acta Physica Sinica, 2017, 66(12): 120501. doi: 10.7498/aps.66.120501
[2]	Jiao Shang-Bin, Sun Di, Liu Ding, Xie Guo, Wu Ya-Li, Zhang Qing. Vibrational resonance in a periodic potential system with stable noise. Acta Physica Sinica, 2017, 66(10): 100501. doi: 10.7498/aps.66.100501
[3]	Li Shuang, Li Qian, Li Jiao-Rui. Mechanism for the coexistence phenomenon of random phase suppressing chaos and stochastic resonance in Duffing system. Acta Physica Sinica, 2015, 64(10): 100501. doi: 10.7498/aps.64.100501
[4]	Lai Zhi-Hui, Leng Yong-Gang. Dynamic response and stochastic resonance of a tri-stable system. Acta Physica Sinica, 2015, 64(20): 200503. doi: 10.7498/aps.64.200503
[5]	Ma Zheng-Mu, Jin Yan-Fei. Stochastic resonance in periodic potential driven by dichotomous noise. Acta Physica Sinica, 2015, 64(24): 240502. doi: 10.7498/aps.64.240502
[6]	Ji Yuan-Dong, Zhang Lu, Luo Mao-Kang. Generalized stochastic resonance of power function type single-well system. Acta Physica Sinica, 2014, 63(16): 164302. doi: 10.7498/aps.63.164302
[7]	Xie Wen-Xian, Li Dong-Ping, Xu Peng-Fei, Cai Li, Jin Yan-Fei. Stochastic resonance of a memorial-damped linear system with natural frequency fluctuation. Acta Physica Sinica, 2014, 63(10): 100502. doi: 10.7498/aps.63.100502
[8]	Tian Yan, Huang Li, Luo Mao-Kang. Effects of time-periodic modulation of cross-correlation intensity between noises on stochastic resonance of over-damped linear system. Acta Physica Sinica, 2013, 62(5): 050502. doi: 10.7498/aps.62.050502
[9]	Lai Zhi-Hui, Leng Yong-Gang, Fan Sheng-Bo. Stochastic resonance of cascaded bistable duffing system. Acta Physica Sinica, 2013, 62(7): 070503. doi: 10.7498/aps.62.070503
[10]	Lin Min, Huang Yong-Mei. The mechanism of energy input to bistable system to generate stochastic resonance. Acta Physica Sinica, 2012, 61(22): 220205. doi: 10.7498/aps.61.220205
[11]	Yang Ming, Li Xiang-Lian, Wu Da-Jin. Simulation study on the stochastic resonance of single-mode laser system. Acta Physica Sinica, 2012, 61(16): 160502. doi: 10.7498/aps.61.160502
[12]	Gao Shi-Long, Zhong Su-Chuan, Wei Kun, Ma Hong. Overdamped fractional Langevin equation and its stochastic resonance. Acta Physica Sinica, 2012, 61(10): 100502. doi: 10.7498/aps.61.100502
[13]	Lin Min, Meng Ying. Frequency coupling in bistable system and the mechanism of stochastic resonance. Acta Physica Sinica, 2010, 59(6): 3627-3632. doi: 10.7498/aps.59.3627
[14]	Lin Min, Huang Yong-Mei, Fang Li-Min. The stochastic resonance control of coupled bistable systems. Acta Physica Sinica, 2008, 57(4): 2048-2052. doi: 10.7498/aps.57.2048
[15]	Zhou Bing-Chang, Xu Wei. Stochastic resonance in an asymmetric bistable system driven by correlated noise. Acta Physica Sinica, 2008, 57(4): 2035-2040. doi: 10.7498/aps.57.2035
[16]	Lin Min, Huang Yong-Mei, Fang Li-Min. The feedback control of stochastic resonance in bistable system. Acta Physica Sinica, 2008, 57(4): 2041-2047. doi: 10.7498/aps.57.2041
[17]	Zhou Bing-Chang, Xu Wei. Stochastic resonance in an asymmetric bistable system driven by mixed periodic force and noises. Acta Physica Sinica, 2007, 56(10): 5623-5628. doi: 10.7498/aps.56.5623
[18]	Ning Li-Juan, Xu Wei. Stochastic resonance in optical bistable system. Acta Physica Sinica, 2007, 56(4): 1944-1947. doi: 10.7498/aps.56.1944
[19]	Jin Yan-Fei, Xu Wei, Li Wei, Xu Meng. Stochastic resonance for periodically modulated noise in a linear system. Acta Physica Sinica, 2005, 54(6): 2562-2567. doi: 10.7498/aps.54.2562
[20]	Leng Yong-Gang, Wang Tai-Yong, Guo Yan, Wang Wen-Jin, Hu Shi-Guang. Stochastic resonance behaviors of bistable systems connected in series. Acta Physica Sinica, 2005, 54(3): 1118-1125. doi: 10.7498/aps.54.1118

Catalog

Vol. 71, Issue 8 - 2022-04-20

Metrics

Abstract views: 4946
PDF Downloads: 124
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板