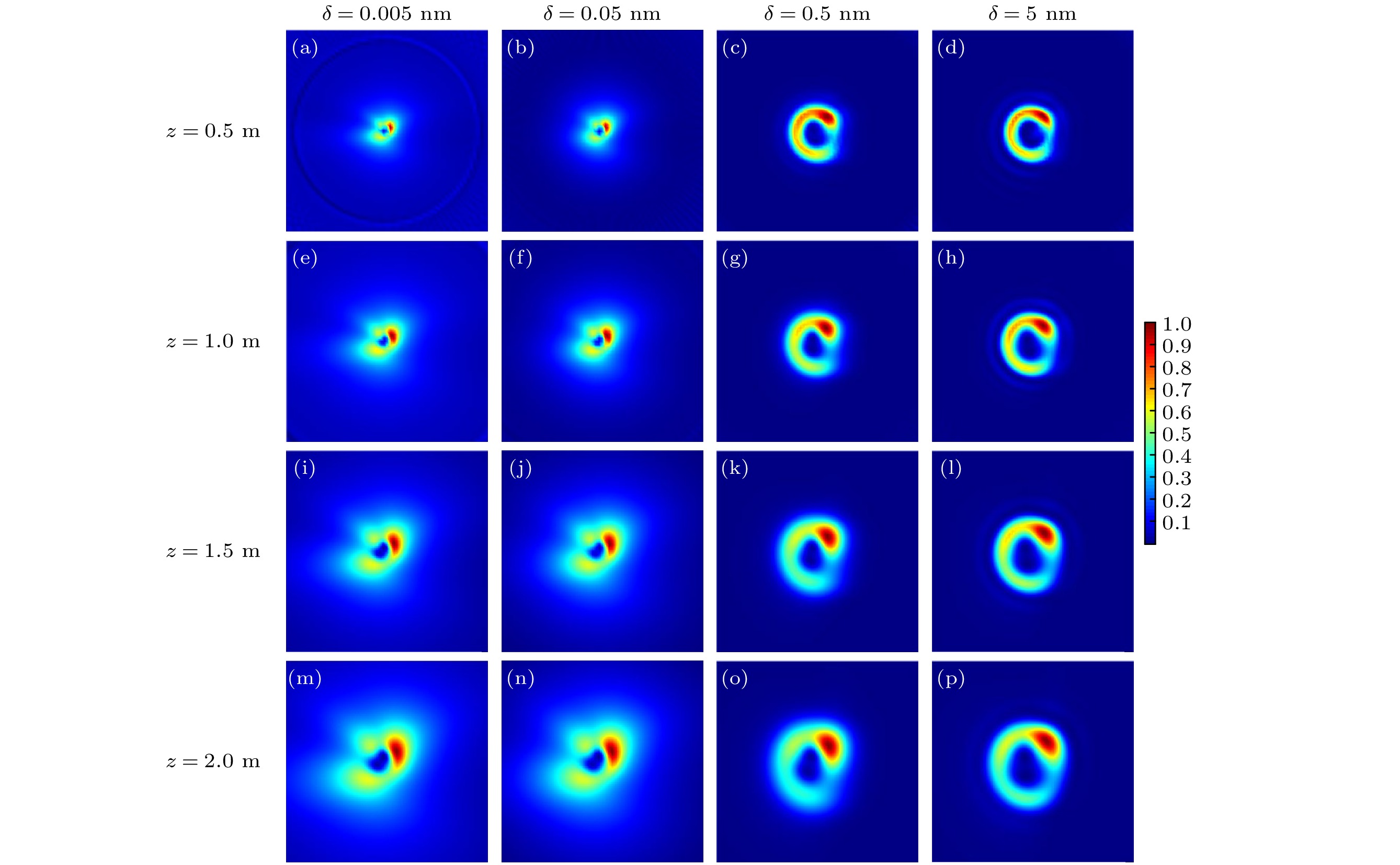
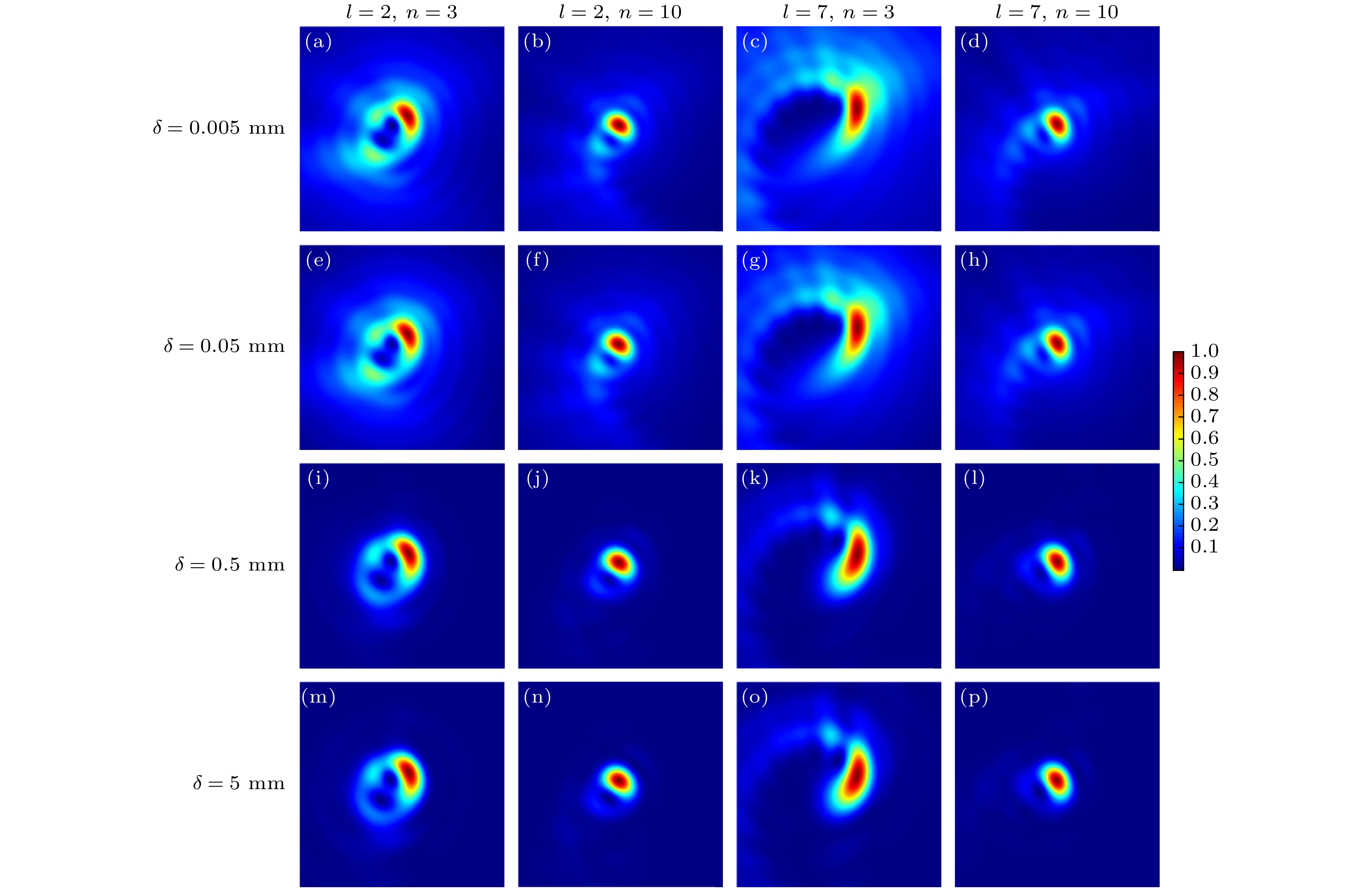
-
In this work, the propagation properties of partially coherent power-exponent-phase vortex beam are studied. Firstly, the propagation model of partially coherent power-exponent-phase vortex beam is established. Then, the propagation properties of partially coherent power-exponent-phase vortex beams in free space and ABCD optical system are simulated. The results show that when power-exponent-phase vortex beams propagate in free space, the topological charge, power order and coherence length have a great influence on the distribution of light intensity, and the area of light spot gradually increases with the increase of propagation distance. When the beam propagates in a focusing system, the changes of topological charge and power order will affect the light intensity distribution, while the coherence length has little effect on the overall intensity distribution of the beam, but only the quality of the spot. The research results of this work reveal the propagation properties of partially coherent power-exponent-phase vortex beam, which will lay a theoretical foundation for its applications in optical capture and other fields, and has important significance in promoting the theory and applications of new light field regulation.
-
Keywords:
- partially coherent beam /
- power-exponent-phase vortex beam /
- propagation properties /
- intensity distribution
[1] Yao A M, Padgett M J 2011 Adv. Opt. Photonics 3 161
Google Scholar
[2] Ng J, Lin Z, Chan C T 2010 Phys. Rev. Lett. 104 103601
Google Scholar
[3] Willner A E, Huang H, Yan Y, Ren Y, Ahmed N, Xie G 2015 Adv. Opt. Photonics 7 66
Google Scholar
[4] Huang K, Liu H, Restuccia S, Mehmood M Q, Mei S T, Giovannini D 2018 Light Sci. Appl. 7 17156
Google Scholar
[5] Ni J, Wang C, Zhang C, Hu Y, Yang L, Lao Z 2017 Light Sci. Appl. 26 e17011
[6] Chow T W, Pechprasarn S, Meng J 2016 Opt. Express 24 10797
Google Scholar
[7] Li P, Liu S, Peng T, Xie G, Gan X, Zhao J 2014 Opt. Express 22 7598
Google Scholar
[8] Lao G, Zhang Z, Zhao D 2016 Opt. Express 24 18082
Google Scholar
[9] Pei Z, Huang S, Chen Y 2021 J. Mod. Opt. 68 224
Google Scholar
[10] Wang F, Liu X, Yuan Y 2013 Opt. Lett. 38 1814
Google Scholar
[11] Yu J, Zhu X, Lin S 2020 Opt. Lett. 45 3824
Google Scholar
[12] Cai Y J, Zhu S Y 2004 Opt. Lett. 29 2716
[13] Clark J N, Huang X, Harder R, Robinson I K 2012 Nat. Commun. 3 1
[14] Zhao C, Cai Y J, Lu X, Eyyuboğlu H T 2009 Opt. Express 17 1753
Google Scholar
[15] Wang F, Cai Y J, Dong Y 2012 Appl. Phys. Lett. 100 051108
Google Scholar
[16] 刘森森, 宋华冬, 林伟强, 陈旭东, 蒲继雄 2019 68 074201
Liu S S, Song H D, Lin W Q, Chen X D, Pu J X 2019 Acta Phys. Sin. 68 074201
[17] Xu H F, Zhou Y, Wu H W 2018 Opt. Express 26 20076
Google Scholar
[18] 张磊, 陈子阳, 崔省伟, 刘绩林, 蒲继雄 2015 64 034205
Zhang L, Chen Z Y, Cui X W, Liu J L, Pu J X 2015 Acta Phys. Sin. 64 034205
[19] 王飞, 余佳益, 刘显龙, 蔡阳健 2018 67 184203
Wang F, Yu J Y, Liu X L, Cai Y J 2018 Acta Phys. Sin. 67 184203
[20] Xu H F, Zhang R, Sheng Z Q 2019 Opt. Express 27 23959
Google Scholar
[21] Dong M, Zhao C L, Cai Y J 2021 Sci. China. Phys. Mech. 64 1
Google Scholar
[22] Liu X, Zeng J, Cai Y J 2019 Adv. Phys. X 4 1626766
[23] Stahl C S D 2018 (The University of North Carolina at Charlotte).
[24] Wolf E 2017 Introduction to the Theory of Coherence and Polarization of Light (Cambridge University Press) p88
[25] Mandel L, Wolf E 1995 Optical Coherence and Quantum Optics (Cambridge University Press) p276
[26] Ma P, Kacerovská B, Khosravi R 2019 Appl. Sci. 9 2084
Google Scholar
[27] Zhao C, Dong Y, Wang Y 2012 Appl. Phys. B 109 345
Google Scholar
[28] Wang T, Pu J, Chen Z 2008 Opt. Eng. 47 036002
Google Scholar
-
图 1 (a), (c) 拓扑荷数l=4的涡旋光束和(b), (d)拓扑荷数l = 4及幂指数n = 2的幂指数相位涡旋光束在源平面上的相位和强度分布
Figure 1. Phase and intensity distributions of (a), (c) vortex beam (l = 4) and (b), (d) power-exponent-phase vortex beam (l = 4, n = 2) on the source plane.
图 2 部分相干幂指数相位涡旋光束的传输特性与拓扑荷数l和幂指数n的关系
Figure 2. Relationship between propagation properties of partially coherent power-exponent-phase vortex beams with the topological charge l and power order n
图 3 部分相干幂指数相位涡旋光束传输特性与相干长度δ和传输距离z的关系
Figure 3. Relationship between propagation properties of partially coherent power-exponent-phase vortex beams with the coherence length δ and propagation distance z.
图 4 聚焦系统示意图
Figure 4. Schematic diagram of focusing system.
图 5 相干长度δ = 0.5 mm时, 部分相干幂指数相位涡旋光束聚焦特性与幂指数n、拓扑荷数l的关系
Figure 5. Relationship between focusing properties of partially coherent power-exponent-phase vortex beams and power order n and topological charge l with coherent length δ = 0.5 mm.
图 6 部分相干幂指数相位涡旋的聚焦特性与相干长度δ的关系
Figure 6. Relationship between focusing properties of partially coherent power-exponent-phase vortex beams and coherent length δ
-
[1] Yao A M, Padgett M J 2011 Adv. Opt. Photonics 3 161
Google Scholar
[2] Ng J, Lin Z, Chan C T 2010 Phys. Rev. Lett. 104 103601
Google Scholar
[3] Willner A E, Huang H, Yan Y, Ren Y, Ahmed N, Xie G 2015 Adv. Opt. Photonics 7 66
Google Scholar
[4] Huang K, Liu H, Restuccia S, Mehmood M Q, Mei S T, Giovannini D 2018 Light Sci. Appl. 7 17156
Google Scholar
[5] Ni J, Wang C, Zhang C, Hu Y, Yang L, Lao Z 2017 Light Sci. Appl. 26 e17011
[6] Chow T W, Pechprasarn S, Meng J 2016 Opt. Express 24 10797
Google Scholar
[7] Li P, Liu S, Peng T, Xie G, Gan X, Zhao J 2014 Opt. Express 22 7598
Google Scholar
[8] Lao G, Zhang Z, Zhao D 2016 Opt. Express 24 18082
Google Scholar
[9] Pei Z, Huang S, Chen Y 2021 J. Mod. Opt. 68 224
Google Scholar
[10] Wang F, Liu X, Yuan Y 2013 Opt. Lett. 38 1814
Google Scholar
[11] Yu J, Zhu X, Lin S 2020 Opt. Lett. 45 3824
Google Scholar
[12] Cai Y J, Zhu S Y 2004 Opt. Lett. 29 2716
[13] Clark J N, Huang X, Harder R, Robinson I K 2012 Nat. Commun. 3 1
[14] Zhao C, Cai Y J, Lu X, Eyyuboğlu H T 2009 Opt. Express 17 1753
Google Scholar
[15] Wang F, Cai Y J, Dong Y 2012 Appl. Phys. Lett. 100 051108
Google Scholar
[16] 刘森森, 宋华冬, 林伟强, 陈旭东, 蒲继雄 2019 68 074201
Liu S S, Song H D, Lin W Q, Chen X D, Pu J X 2019 Acta Phys. Sin. 68 074201
[17] Xu H F, Zhou Y, Wu H W 2018 Opt. Express 26 20076
Google Scholar
[18] 张磊, 陈子阳, 崔省伟, 刘绩林, 蒲继雄 2015 64 034205
Zhang L, Chen Z Y, Cui X W, Liu J L, Pu J X 2015 Acta Phys. Sin. 64 034205
[19] 王飞, 余佳益, 刘显龙, 蔡阳健 2018 67 184203
Wang F, Yu J Y, Liu X L, Cai Y J 2018 Acta Phys. Sin. 67 184203
[20] Xu H F, Zhang R, Sheng Z Q 2019 Opt. Express 27 23959
Google Scholar
[21] Dong M, Zhao C L, Cai Y J 2021 Sci. China. Phys. Mech. 64 1
Google Scholar
[22] Liu X, Zeng J, Cai Y J 2019 Adv. Phys. X 4 1626766
[23] Stahl C S D 2018 (The University of North Carolina at Charlotte).
[24] Wolf E 2017 Introduction to the Theory of Coherence and Polarization of Light (Cambridge University Press) p88
[25] Mandel L, Wolf E 1995 Optical Coherence and Quantum Optics (Cambridge University Press) p276
[26] Ma P, Kacerovská B, Khosravi R 2019 Appl. Sci. 9 2084
Google Scholar
[27] Zhao C, Dong Y, Wang Y 2012 Appl. Phys. B 109 345
Google Scholar
[28] Wang T, Pu J, Chen Z 2008 Opt. Eng. 47 036002
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5723
- PDF Downloads: 169
- Cited By: 0
