-
In this paper, the effects of a Gaussian white noise excitation on the one-dimensional Frenkel-Kontorova (FK) model are studied by the stochastic Runge-Kutta method under two different types of substrate cases, i.e. incommensurate case and commensurate case. The noise excitation is considered through the inclusion of a stochastic force via a Langevin molecular dynamics approach, and we uncover the mechanism of nano-friction phenomenon in the FK model driven by the stochastic force. The relationship between the noise intensity and the nano-friction phenomenon, such as hysteresis, maximum static friction force, and the super-lubricity, is investigated by using the stochastic Runge-Kutta algorithm. It is shown that with the increase of noise intensity, the area of the hysteresis becomes smaller and the maximum static friction force tends to decrease, which can promote the generation of super-lubricity. Similar results are obtained from the two cases, in which the ratios of the atomic distance to the period of the substrate potential field are incommensurate and commensurate, respectively. In particular, a suitable noise density gives rise to super-lubricity where the maximum static friction force vanishes. Hence, the noise excitation in this sense is beneficial to the decrease of the hysteresis and the maximum static friction force. Meanwhile, with the appropriate external driving force, the introduction of a noise excitation can accelerate the motion of the system, making the atoms escape from the substrate potential well more easily. But when the chain mobility reaches a saturation state (B = 1), it is no longer affected by the stochastic excitation. Furthermore, the difference between the two circumstances lies in the fact that for the commensurate interface, the influence of the noise is much stronger and more beneficial to triggering the motion of the FK model than for the incommensurate interface since the atoms in the former case are coupled and entrapped more strongly by the substrate potential.
-
Keywords:
- Frenkel-Kontorova model /
- Gaussian white noise /
- hysteresis /
- super-lubricity
[1] 温诗铸 2007 机械工程学报 43 1
Google Scholar
Wen S Z 2007 Chin. J. Mech. Eng. 43 1
Google Scholar
[2] Braun O M, Kivshar Y S 2004 The Frenkel-Kontorova model: Concepts, Methods, and Applications (Berlin: Springer) pp2−20
[3] Wolfgang Q, Josep M B 2019 Eur. Phys. J. B 92 1
Google Scholar
[4] Lei Y M, Zheng F, Shao X Z 2017 Int. J. Bifurcation Chaos 27 1750052
Google Scholar
[5] Zhang Z J, Tang C M, Tong P Q 2016 Phys. Rev. E 93 022216
Google Scholar
[6] Vanossi A, Benassi A, Varini N, Tosatti E 2013 Phys. Rev. B 87 045412
Google Scholar
[7] Zhang J Q, Nie L R, Zhang X Y, Chen R Y 2014 Eur. Phys. J. B 87 1
Google Scholar
[8] 雷佑铭, 李毅伟, 赵云平 2014 63 220502
Google Scholar
LeiY M, Li Y W, Zhao Y P 2014 Acta Phys. Sin. 63 220502
Google Scholar
[9] Yung K L, Lei Y M, Xu Y 2010 Chin. Phys. B 19 010503
Google Scholar
[10] 杨阳, 王苍龙, 段文山, 石玉仁, 陈建敏 2012 61 130501
Google Scholar
Yang Y, Wang C L, Duan W S, Shi Y R, Chen J M 2012 Acta Phys. Sin. 61 130501
Google Scholar
[11] Yang Y, Duan W S, Yang L, Chen J M, Lin M M 2011 Europhys. Lett. 93 16001
Google Scholar
[12] Vanossi A, Santoro G, Bortolani V 2004 J. Phys. Condens. Matter 16 2895
Google Scholar
[13] Braun O M, Bishop A, Röder J 1997 Phys. Rev. Lett 79 3692
Google Scholar
[14] Vanossi A, Röder J, Bishop A, Bortolani V 2003 Phys. Rev. E 67 016605
Google Scholar
[15] Tekić J, Hu B 2008 Phys. Rev. B 78 104305
Google Scholar
[16] Tekić J, He D, Hu B 2009 Phys. Rev. E 79 036604
Google Scholar
[17] Tekić J, Hu B 2010 Phys. Rev. E 81 036604
Google Scholar
[18] Hu B, Tekić J 2007 Phys. Rev. E 75 056608
Google Scholar
[19] Capozza R, Vanossi A, Vezzani A, Zapperi S 2012 Tribol. Lett. 48 95
Google Scholar
[20] Braun O M, Zhang H, Hu B, Tekić J 2003 Phys. Rev. E 67 066602
Google Scholar
[21] Capozza R, Vanossi A, Vezzani A, Zapperi S 2009 Phys. Rev. Lett. 103 085502
Google Scholar
[22] Lin M M, Duan W S, Chen J M 2010 Chin. Phys. B 19 026201
Google Scholar
[23] Vanossi A, Braun O M 2007 J. Phys. Condens. Matter 19 305017
Google Scholar
[24] Guerra R, Vanossi A, Ferrario M 2007 Surf. Sci. 601 3676
Google Scholar
[25] Braun O M, Dauxois T, Paliy M V, Peyrard M 1997 Phys. Rev. E 55 3598
Google Scholar
[26] 李晓礼, 刘锋, 林麦麦, 陈建敏, 段文山 2010 59 2589
Google Scholar
Li X L, Liu F, Lin M M, Chen J M, Duan W S 2010 Acta Phys. Sin. 59 2589
Google Scholar
[27] 秦文新 2017 中国科学: 数学 47 1853
Google Scholar
Qin W X 2017 Sci. Sin. Math. 47 1853
Google Scholar
[28] Honeycutt R 1992 Phys. Rev. A 45 600
Google Scholar
[29] 许爱国, 王光瑞, 陈式刚, 杨展如 1999 物理学进展 19 109
Google Scholar
Xu A G, Wang G R, Chen S G, Yang Z R 1999 Prog. Phys. 19 109
Google Scholar
-
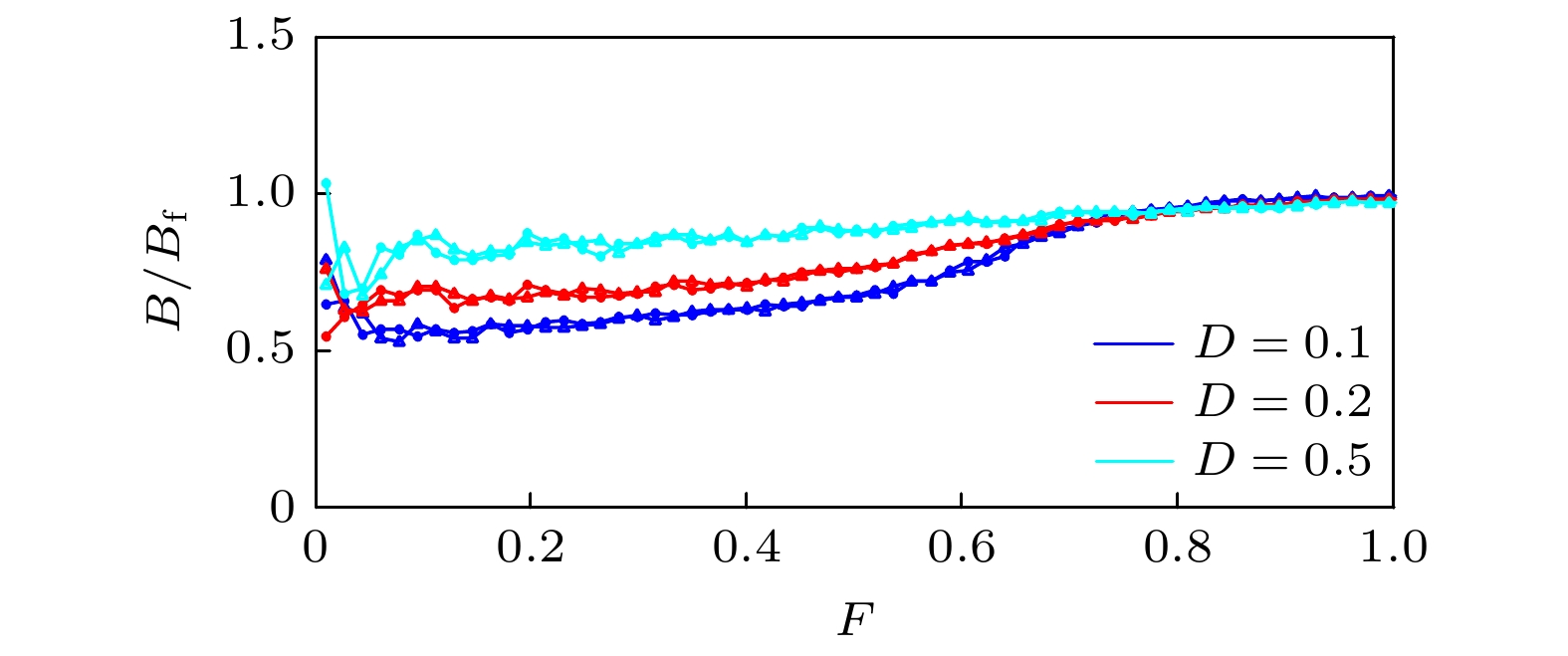
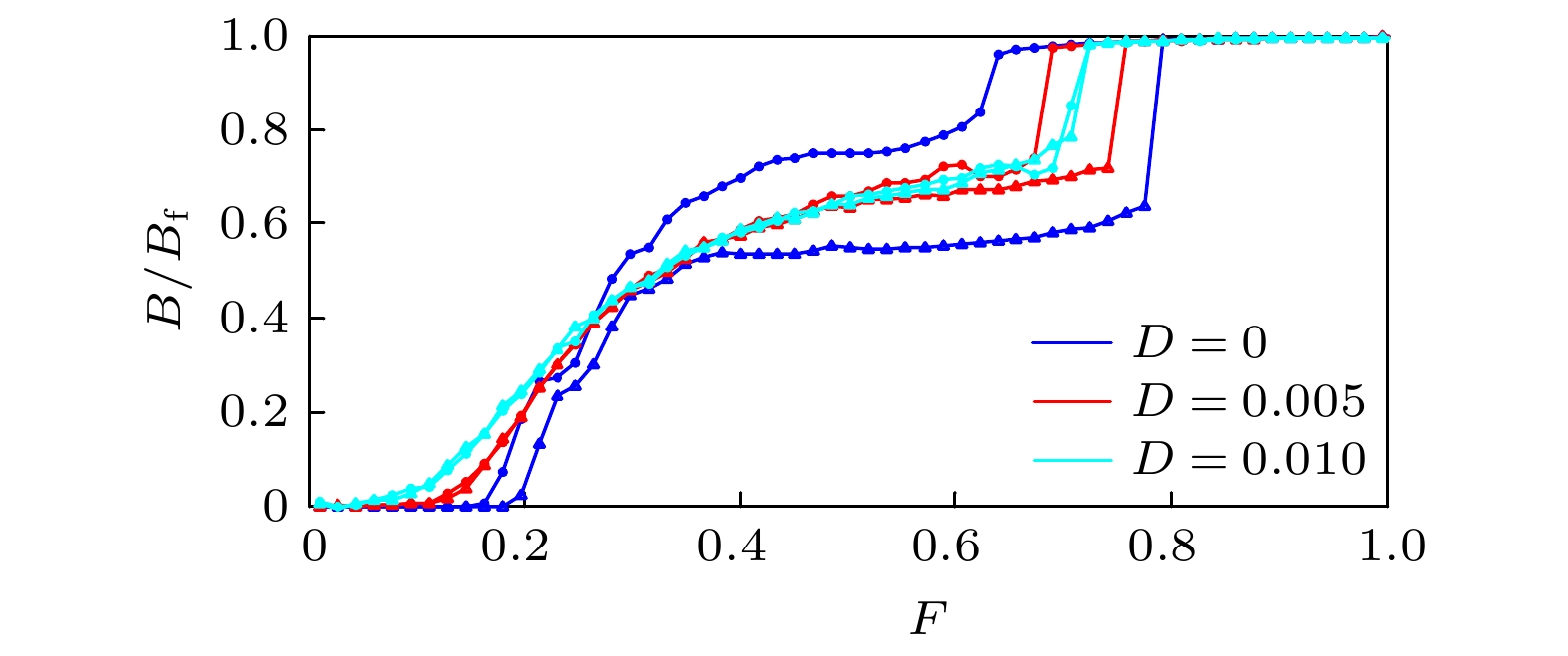
图 1 D = 0, 0.005, 0.010时, 非公度情形下系统机动性能B随外力F的改变的变化规律(图中三角形和原点分别表示外力F绝热增加和减小的过程)
Figure 1. Noise effects on static friction and hysteresis of the
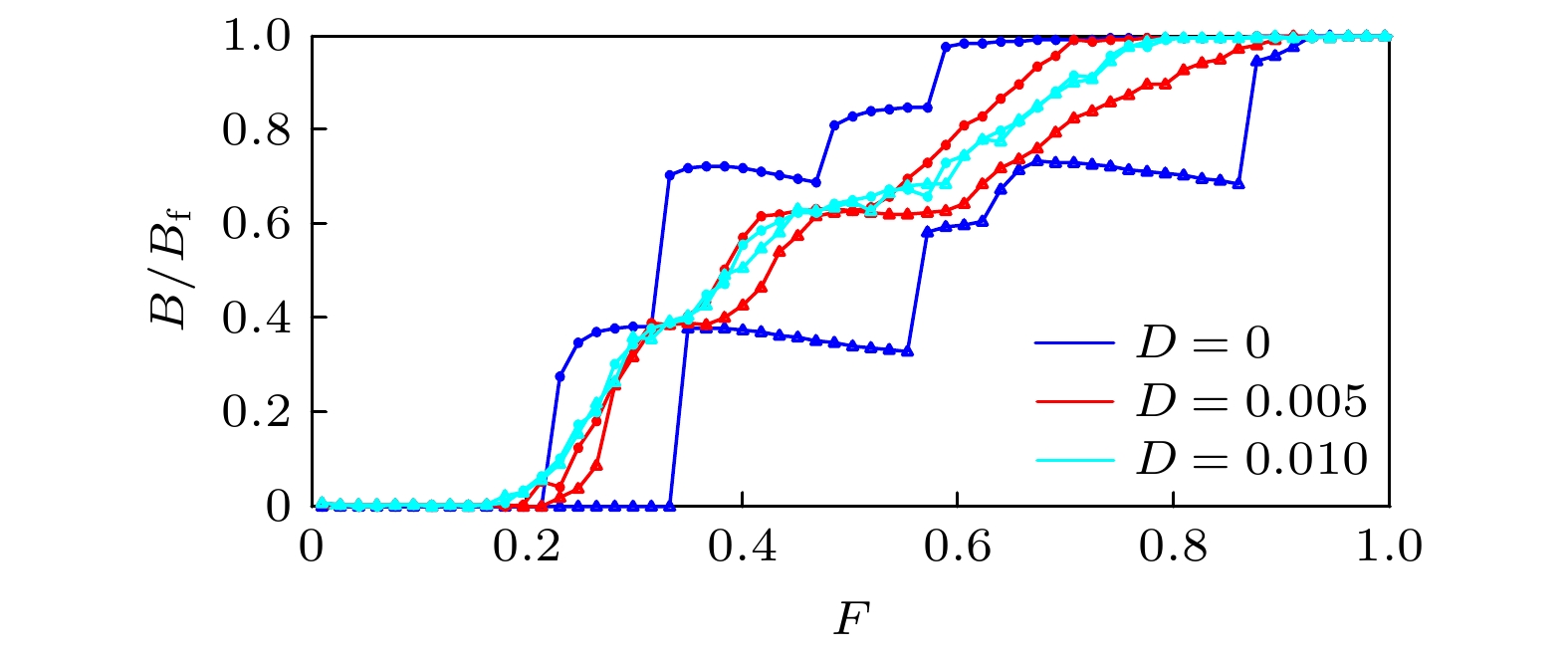
$B(F)$ characteristics for the incommensurate case when D = 0, 0.005, 0.010. Triangles and circles denote, respectively, the adiabatic increasing and decreasing process of F.
图 2 D = 0.1, 0.2, 0.5时, 非公度情形下系统机动性能B随外力F的改变的变化规律
Figure 2. Noise effects on static friction and hysteresis of the
$B(F)$ characteristics for the incommensurate case when D = 0.1, 0.2, 0.5.
图 3 非公度情形下最大静摩擦力
${F_{\rm{s}}}$ 随噪声强度D的改变的变化规律Figure 3. Noise effects on maximum static friction for the incommensurate case.
图 4 D = 0, 0.005, 0.010时, 公度情形下系统机动性能B随外力F的改变的变化规律(图中三角形和原点分别表示外力F绝热增加和减小的过程)
Figure 4. Noise effects on static friction and hysteresis of the
$B(F)$ characteristics for the commensurate case when D = 0, 0.005, 0.010. Triangles and circles denote, respectively, the adiabatic increasing and decreasing process of F.
图 5 D = 0.1, 0.2, 0.5时公度情形下系统机动性能B随外力F的改变的变化规律
Figure 5. Noise effects on static friction and hysteresis of the
$B(F)$ characteristics for the commensurate case when D = 0.1, 0.2, 0.5.
图 6 公度与非公度情形下最大静摩擦力
${F_{\rm{s}}}$ 随噪声强度D的改变的变化规律Figure 6. Noise effects on maximum static friction for the incommensurate case (blue) and the commensurate case (red)
-
[1] 温诗铸 2007 机械工程学报 43 1
Google Scholar
Wen S Z 2007 Chin. J. Mech. Eng. 43 1
Google Scholar
[2] Braun O M, Kivshar Y S 2004 The Frenkel-Kontorova model: Concepts, Methods, and Applications (Berlin: Springer) pp2−20
[3] Wolfgang Q, Josep M B 2019 Eur. Phys. J. B 92 1
Google Scholar
[4] Lei Y M, Zheng F, Shao X Z 2017 Int. J. Bifurcation Chaos 27 1750052
Google Scholar
[5] Zhang Z J, Tang C M, Tong P Q 2016 Phys. Rev. E 93 022216
Google Scholar
[6] Vanossi A, Benassi A, Varini N, Tosatti E 2013 Phys. Rev. B 87 045412
Google Scholar
[7] Zhang J Q, Nie L R, Zhang X Y, Chen R Y 2014 Eur. Phys. J. B 87 1
Google Scholar
[8] 雷佑铭, 李毅伟, 赵云平 2014 63 220502
Google Scholar
LeiY M, Li Y W, Zhao Y P 2014 Acta Phys. Sin. 63 220502
Google Scholar
[9] Yung K L, Lei Y M, Xu Y 2010 Chin. Phys. B 19 010503
Google Scholar
[10] 杨阳, 王苍龙, 段文山, 石玉仁, 陈建敏 2012 61 130501
Google Scholar
Yang Y, Wang C L, Duan W S, Shi Y R, Chen J M 2012 Acta Phys. Sin. 61 130501
Google Scholar
[11] Yang Y, Duan W S, Yang L, Chen J M, Lin M M 2011 Europhys. Lett. 93 16001
Google Scholar
[12] Vanossi A, Santoro G, Bortolani V 2004 J. Phys. Condens. Matter 16 2895
Google Scholar
[13] Braun O M, Bishop A, Röder J 1997 Phys. Rev. Lett 79 3692
Google Scholar
[14] Vanossi A, Röder J, Bishop A, Bortolani V 2003 Phys. Rev. E 67 016605
Google Scholar
[15] Tekić J, Hu B 2008 Phys. Rev. B 78 104305
Google Scholar
[16] Tekić J, He D, Hu B 2009 Phys. Rev. E 79 036604
Google Scholar
[17] Tekić J, Hu B 2010 Phys. Rev. E 81 036604
Google Scholar
[18] Hu B, Tekić J 2007 Phys. Rev. E 75 056608
Google Scholar
[19] Capozza R, Vanossi A, Vezzani A, Zapperi S 2012 Tribol. Lett. 48 95
Google Scholar
[20] Braun O M, Zhang H, Hu B, Tekić J 2003 Phys. Rev. E 67 066602
Google Scholar
[21] Capozza R, Vanossi A, Vezzani A, Zapperi S 2009 Phys. Rev. Lett. 103 085502
Google Scholar
[22] Lin M M, Duan W S, Chen J M 2010 Chin. Phys. B 19 026201
Google Scholar
[23] Vanossi A, Braun O M 2007 J. Phys. Condens. Matter 19 305017
Google Scholar
[24] Guerra R, Vanossi A, Ferrario M 2007 Surf. Sci. 601 3676
Google Scholar
[25] Braun O M, Dauxois T, Paliy M V, Peyrard M 1997 Phys. Rev. E 55 3598
Google Scholar
[26] 李晓礼, 刘锋, 林麦麦, 陈建敏, 段文山 2010 59 2589
Google Scholar
Li X L, Liu F, Lin M M, Chen J M, Duan W S 2010 Acta Phys. Sin. 59 2589
Google Scholar
[27] 秦文新 2017 中国科学: 数学 47 1853
Google Scholar
Qin W X 2017 Sci. Sin. Math. 47 1853
Google Scholar
[28] Honeycutt R 1992 Phys. Rev. A 45 600
Google Scholar
[29] 许爱国, 王光瑞, 陈式刚, 杨展如 1999 物理学进展 19 109
Google Scholar
Xu A G, Wang G R, Chen S G, Yang Z R 1999 Prog. Phys. 19 109
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4667
- PDF Downloads: 68
- Cited By: 0
