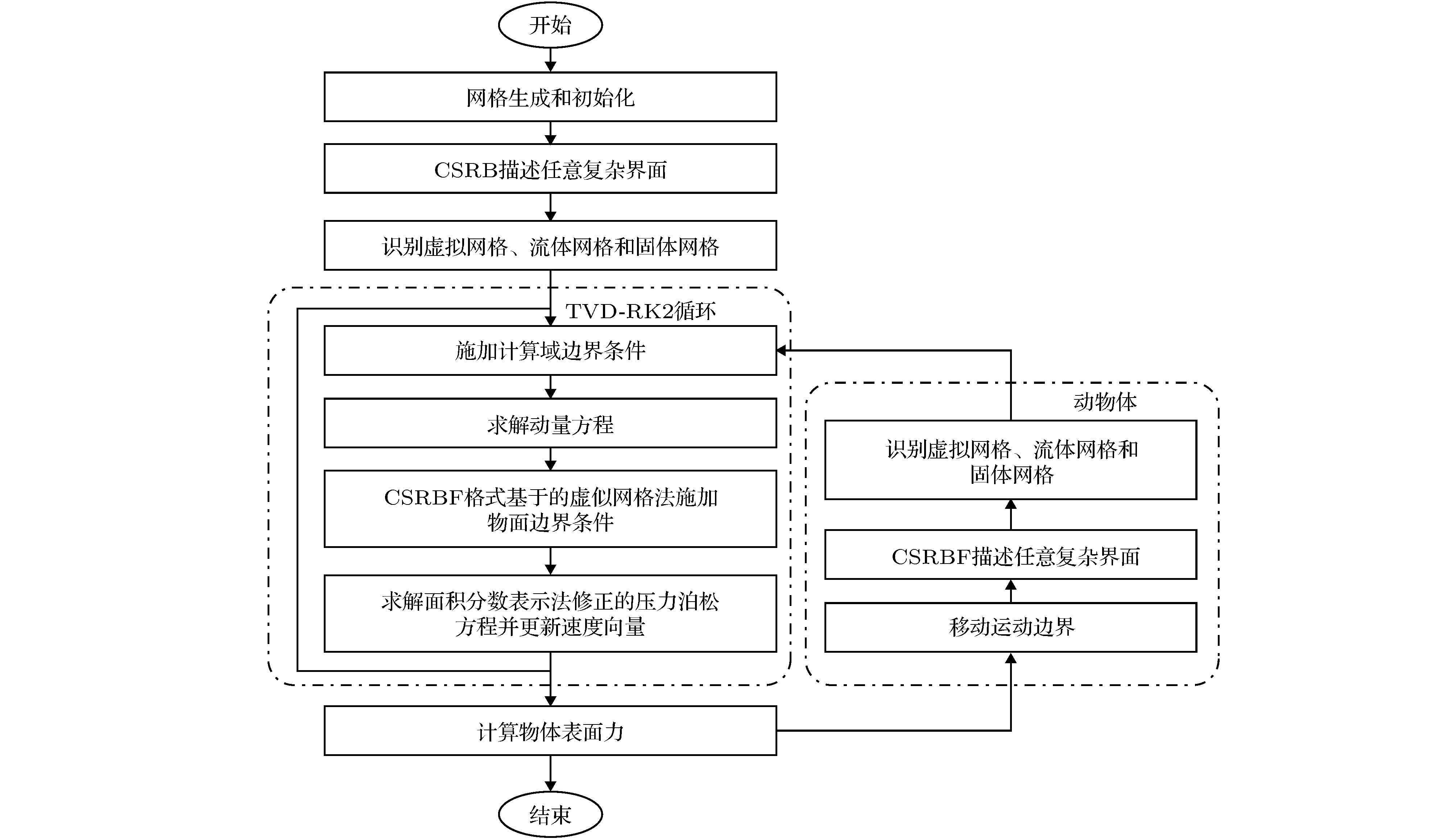
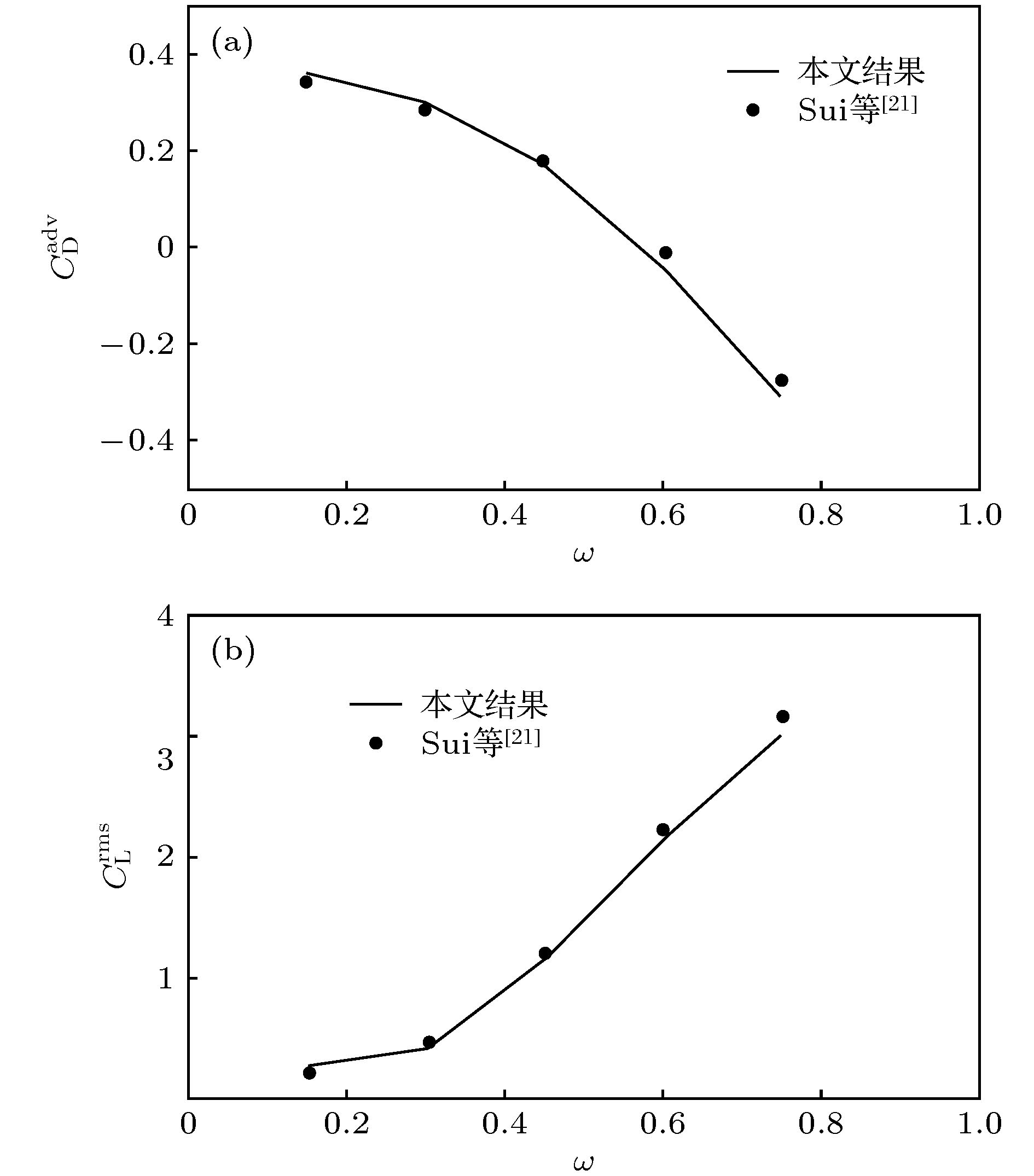
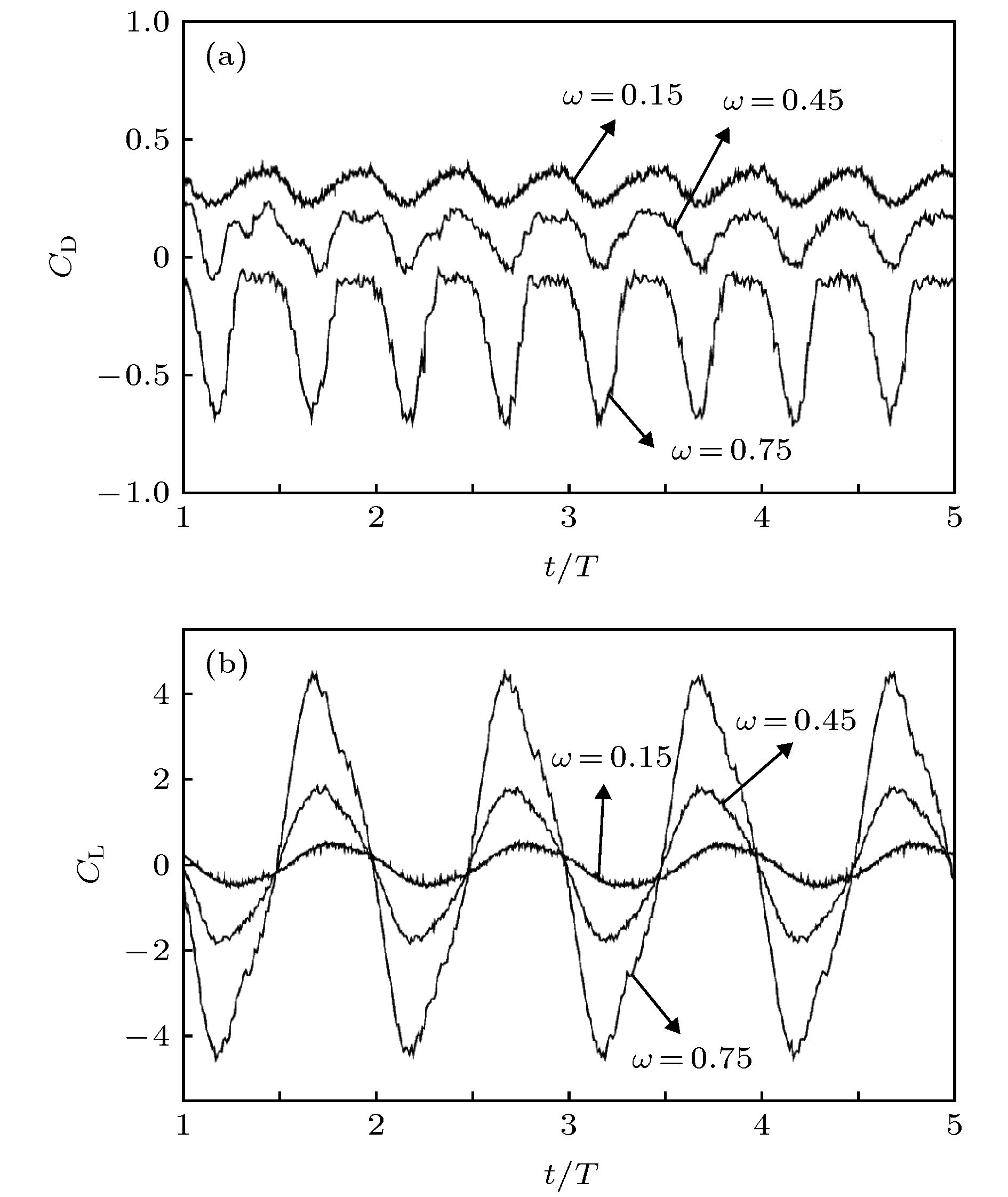
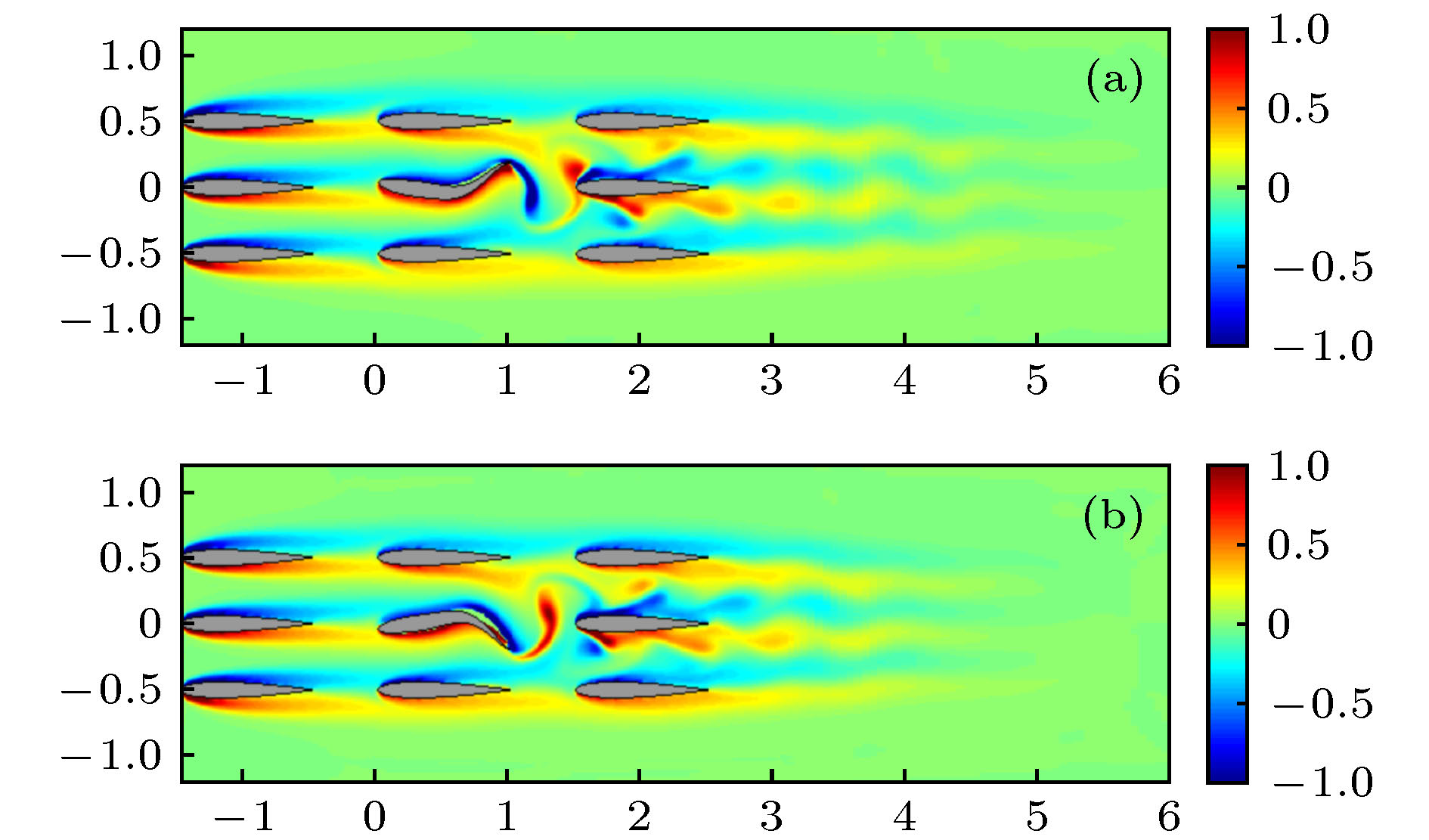
-
Studies on hydrodynamic characteristics of viscous incompressible flows around flexible hydrofoils are of practical importance for the design and performance optimization of marine structures such as ship rudders and stabilizing fins. The aim of this paper is to extend a radial basis function based ghost cell method to simulate flows around single or multiple flexible moving hydrofoils in array arrangement. The numerical model is based on a ghost cell finite difference method for considering the influence of the immersed boundaries on the flow. Also, a compact supported radial basis function (CSRBF) is introduced to track the complex flexible boundary with some controlling points of the body surface. Based on the present method, the uniform flow around a flexible hydrofoil swimming like a fish is simulated. Good grid convergence of drag and lift coefficients demonstrates the accuracy and reliability of the present method. Also, the hydrodynamics patterns of the flexible hydrofoil under different oscillation frequencies are studied. Further, the thrust generation mechanism of the hydrofoil is explained. Afterwards, flows around the undulating hydrofoils in array arrangement are simulated. The force coefficients and wake patterns under different distances and oscillation frequencies are investigated. It is observed that the thrust coefficients of the hydrofoils under narrow arrangement and high oscillation frequencies have significant amplification effects. In addition, the critical frequency at zero thrust reduces.
-
Keywords:
- Cartesian grid /
- radial basis function /
- flexible hydrofoils /
- array arrangement
[1] Zabihi M, Lari K, Amiri H 2017 J. Mech. Sci. Technol. 31 3539
Google Scholar
[2] Yang J M 2016 J. Hydrodyn. Ser. B 28 713
Google Scholar
[3] 王力, 田方宝 2018 中国科学: 物理学 力学 天文学 48 094703
Google Scholar
Wang L, Tian F B 2018 Sci. China Phys. Mech. Astron. 48 094703
Google Scholar
[4] Al-Marouf M, Samtaney R 2017 J. Comput. Phys. 337 339
Google Scholar
[5] Huang W X, Chang C B, Sung H J 2011 J. Comput. Phys. 230 5061
Google Scholar
[6] Tullio M D D, Pascazio G 2016 J. Comput. Phys. 325 201
Google Scholar
[7] 吴晓笛, 刘华坪, 陈浮 2017 22 224702
Google Scholar
Wu X D, Liu H P, Chen F 2017 Acta Phys. Sin. 22 224702
Google Scholar
[8] Yeo K S, Ang S J, Shu C 2010 Comput. Fluids 39 403
Google Scholar
[9] Tian F B, Wang W, Wu J, Sui Y 2016 Comput. Fluids 124 1
Google Scholar
[10] Bergmann M, Iollo A, Mittal R 2014 Bioinspiration Biomimetics 9 046001
Google Scholar
[11] Khalid M S U, Akhtar I, Dong H 2016 J. Fluids Struct. 66 19
Google Scholar
[12] Khalid M S U, Akhtar I, Imtiaz H, Dong H, Wu B 2018 Ocean Eng. 157 108
Google Scholar
[13] Mittal R, Dong H, Bozkurttas M, Najjar F M, Vargas A, Loebbecke A V 2008 J. Comput. Phys. 227 4825
Google Scholar
[14] 王亮, 吴锤结 2011 力学学报 43 18
Google Scholar
Wang L, Wu C J 2011 Chin. J. Theor. Appl. Mech. 43 18
Google Scholar
[15] 王文全 2014 计算力学学报 31 646
Google Scholar
Wang W Q 2014 Chin. J. Comput. Mech. 31 646
Google Scholar
[16] 辛建建, 石伏龙, 金秋 2017 66 186
Xin J J, Shi F L, Jin Q 2017 Acta Phys. Sin. 66 186
[17] Xin J J, Shi F L, Jin Q, Lin C 2018 Comput. Fluids 176 210
Google Scholar
[18] Leer B V 1979 J. Comput. Phys. 32 101
Google Scholar
[19] Van d V H A, Kohn R V, Iserles A, Ciarlet P G, Wright M H 2006 Iterative Krylov Methods for Large Linear Systems (Cambridge: Cambridge University Press) pp133–135
[20] Liu G R, Gu Y T 2005 An Introduction to Meshfree Methods and Their Programming (Netherlands: Springer) p73
[21] Sui Y, Chew Y T, Roy P, Low H T 2007 Int. J. Numer. Methods Fluids 53 1727
Google Scholar
-
图 1 虚拟网格法的二维插值格式 (a)无虚拟网格; (b)一个虚拟网格; (c)两个虚拟网格
Figure 1. Two-dimensional interpolation stencil of the ghost cell method: (a) No ghost cells; (b) one ghost cell; (c) two ghost cells.
图 2 静止或运动边界流动求解算法的流程图
Figure 2. Flowchart of numerical algorithm for stationary or moving boundary flows.
图 3 五个频率下的力系数比较 (a) 平均阻力系数; (b) 均方根升力系数
Figure 3. Comparison of force coefficients under five oscillation frequencies: (a) Average drag coefficient; (b) root mean square lift coefficient.
图 4 三个频率下升阻力系数随无因次时间的变化趋势 (a) 阻力系数; (b) 升力系数
Figure 4. Variation of drag and lift coefficients with the dimensionless time under three oscillation frequencies: (a) Drag coefficient; (b) lift coefficient.
图 5
$\omega $ = 0.15时在两个时刻的局部瞬时涡等值线 (a)$\theta = $ $ {\text{π}}/2$ ; (b)$\theta = 3{\text{π}}/2$ Figure 5. Local instantaneous vortex contours for
$\omega $ = 0.15 at two moments: (a)$\theta = {\text{π}}/2$ ; (b)$\theta = 3{\text{π}}/2$ .
图 7
$\omega $ = 0.75时在两个时刻的局部瞬时涡等值线 (a)$\theta = $ ${\text{π}}/2$ ; (b)$\theta = 3{\text{π}}/2$ Figure 7. Local instantaneous vortex contours for
$\omega $ = 0.75 at two moments: (a)$\theta = {\text{π}}/2$ ; (b)$\theta = 3{\text{π}}/2$ .
图 6
$\omega $ = 0.45时在两个时刻的局部瞬时涡等值线 (a)$\theta = $ $ {\text{π}}/2$ ; (b)$\theta = 3{\text{π}}/2$ Figure 6. Local instantaneous vortex contours for
$\omega $ = 0.45 at two moments: (a)$\theta = {\text{π}}/2$ ; (b)$\theta = 3{\text{π}}/2$ .
图 8 阵列布置水翼游动的几何模型
Figure 8. Geometrical model of the undulating hydrofoil in array arrangement.
图 9 三个间距下群游中间位置水翼和单水翼在五个频率下的力系数比较 (a)平均阻力系数; (b)均方根升力系数
Figure 9. Comparison of force coefficients between the central hydrofoil in array arrangement for three gap distances and the single hydrofoil under five frequencies: (a) Average drag coefficient; (b) root mean square lift coefficient.
图 10 群游中间位置水翼在三个频率下升阻力系数随无因次时间的变化趋势 (a)阻力系数; (b)升力系数
Figure 10. Variation of drag and lift coefficients on the central hydrofoil in array arrangement with the dimensionless time under three oscillation frequencies: (a) Drag coefficient; (b) lift coefficient.
图 11
$\omega $ = 0.15时在两时刻的水翼群游局部涡场图 (a)$\theta = {\text{π}}/2$ ; (b)$\theta = 3{\text{π}}/2$ Figure 11. Local instantaneous vortex contours of undulating hydrofoils in array arrangement for
$\omega $ = 0.15 at two moments: (a)$\theta = {\text{π}}/2$ ; (b)$\theta = 3{\text{π}}/2$ .
图 12
$\omega $ = 0.45时在两时刻的水翼群游局部涡场图 (a)$\theta = $ $ {\text{π}}/2$ ; (b)$\theta = 3{\text{π}}/2$ Figure 12. Local instantaneous vortex contours of undulating hydrofoils in array arrangement for
$\omega $ = 0.45 at two moments: (a)$\theta = {\text{π}}/2$ ; (b)$\theta = 3{\text{π}}/2$ .
图 13
$\omega $ = 0.75时在两时刻的水翼群游局部涡场图 (a)$\theta = $ $ {\text{π}}/2$ ; (b)$\theta = 3{\text{π}}/2$ Figure 13. Local instantaneous vortex contours of undulating hydrofoils in array arrangement for
$\omega $ = 0.75 at two moments: (a)$\theta = {\text{π}}/2$ ; (b)$\theta = 3{\text{π}}/2$ . -
[1] Zabihi M, Lari K, Amiri H 2017 J. Mech. Sci. Technol. 31 3539
Google Scholar
[2] Yang J M 2016 J. Hydrodyn. Ser. B 28 713
Google Scholar
[3] 王力, 田方宝 2018 中国科学: 物理学 力学 天文学 48 094703
Google Scholar
Wang L, Tian F B 2018 Sci. China Phys. Mech. Astron. 48 094703
Google Scholar
[4] Al-Marouf M, Samtaney R 2017 J. Comput. Phys. 337 339
Google Scholar
[5] Huang W X, Chang C B, Sung H J 2011 J. Comput. Phys. 230 5061
Google Scholar
[6] Tullio M D D, Pascazio G 2016 J. Comput. Phys. 325 201
Google Scholar
[7] 吴晓笛, 刘华坪, 陈浮 2017 22 224702
Google Scholar
Wu X D, Liu H P, Chen F 2017 Acta Phys. Sin. 22 224702
Google Scholar
[8] Yeo K S, Ang S J, Shu C 2010 Comput. Fluids 39 403
Google Scholar
[9] Tian F B, Wang W, Wu J, Sui Y 2016 Comput. Fluids 124 1
Google Scholar
[10] Bergmann M, Iollo A, Mittal R 2014 Bioinspiration Biomimetics 9 046001
Google Scholar
[11] Khalid M S U, Akhtar I, Dong H 2016 J. Fluids Struct. 66 19
Google Scholar
[12] Khalid M S U, Akhtar I, Imtiaz H, Dong H, Wu B 2018 Ocean Eng. 157 108
Google Scholar
[13] Mittal R, Dong H, Bozkurttas M, Najjar F M, Vargas A, Loebbecke A V 2008 J. Comput. Phys. 227 4825
Google Scholar
[14] 王亮, 吴锤结 2011 力学学报 43 18
Google Scholar
Wang L, Wu C J 2011 Chin. J. Theor. Appl. Mech. 43 18
Google Scholar
[15] 王文全 2014 计算力学学报 31 646
Google Scholar
Wang W Q 2014 Chin. J. Comput. Mech. 31 646
Google Scholar
[16] 辛建建, 石伏龙, 金秋 2017 66 186
Xin J J, Shi F L, Jin Q 2017 Acta Phys. Sin. 66 186
[17] Xin J J, Shi F L, Jin Q, Lin C 2018 Comput. Fluids 176 210
Google Scholar
[18] Leer B V 1979 J. Comput. Phys. 32 101
Google Scholar
[19] Van d V H A, Kohn R V, Iserles A, Ciarlet P G, Wright M H 2006 Iterative Krylov Methods for Large Linear Systems (Cambridge: Cambridge University Press) pp133–135
[20] Liu G R, Gu Y T 2005 An Introduction to Meshfree Methods and Their Programming (Netherlands: Springer) p73
[21] Sui Y, Chew Y T, Roy P, Low H T 2007 Int. J. Numer. Methods Fluids 53 1727
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6526
- PDF Downloads: 61
- Cited By: 0
