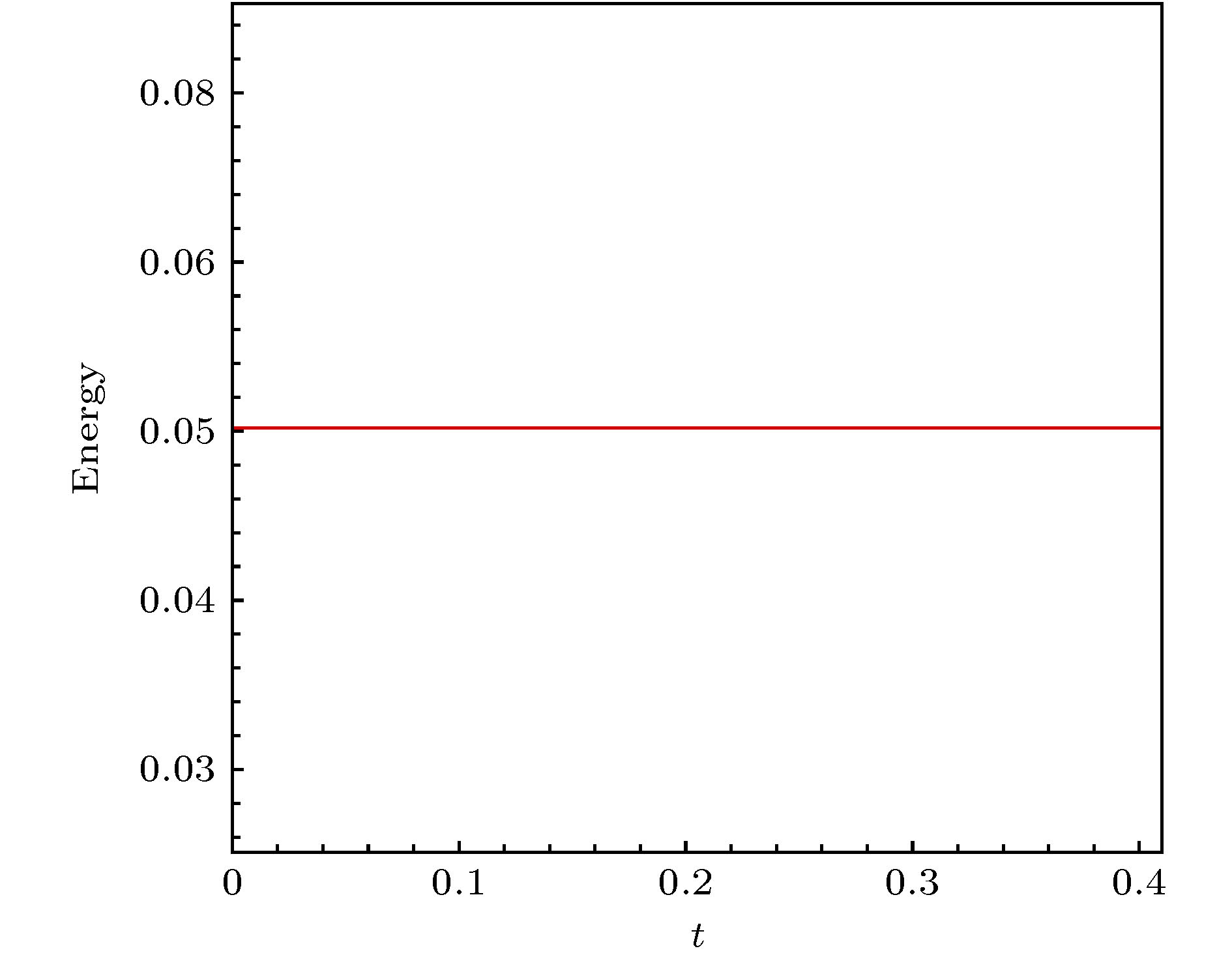
-
The wave propagation is often carried out in complex geological structures. Solving the wave propagation problem effectively in inhomogeneous medium is of great interest and has many applications in physics and engineering. In this paper, the local discontinuous Galekin (LDG) method is applied to the numerical solution of the second-order wave equation. Firstly, the auxiliary variables are introduced, and the second-order wave equations are written as a system of first-order partial differential equations. Then the discontinuous Galerkin format is applied to the corresponding linearized wave equations and adjoint equations. We consider the triangulation in this paper. In order to ensure that the discrete format satisfies the energy conservation, the generalized alternating flux is chosen on the element boundary. We proves that the LDG method satisfies the energy conservation. The exponential integral factor method is used in time discretization. In order to improve the computational efficiency, the Krylov subspace method is used to approximate the product of the exponential matrix and the vector. Numerical examples with exact solutions are given in numerical experiments. The numerical results verify the numerical precision and energy conservation of the LDG method. In addition, the calculation of inhomogeneous medium and complex computational regions are considered. The results show that the LDG method is suitable for simulation of complex structures and propagation in multi-scale structured medium.
-
Keywords:
- wave equation /
- generalized alternating /
- local discontinuous Galerkin method /
- energy conservation
[1] 周聪, 王庆良 2015 64 239101
Google Scholar
Zhou C, Wang Q L 2015 Acta Phys. Sin. 64 239101
Google Scholar
[2] 王飞, 魏兵, 李林茜 2014 63 104101
Google Scholar
Wang F, Wei B, Li L X 2014 Acta Phys. Sin. 63 104101
Google Scholar
[3] 王婷, 崔志文, 刘金霞, 王克协 2018 67 114301
Google Scholar
Wang T, Cui Z W, Liu J X, Wang K X 2018 Acta Phys. Sin. 67 114301
Google Scholar
[4] Kampanis N A, Ekaterinaris J, Dougalis V 2008 Effective Computational Methods for Wave Propagation (Virginia beach: Chapman & Hall/CRC) pp135−164
[5] Sjögreen B, Anders P N 2011 J. Sci. Comput. 52 17
[6] Appelö D, Petersson N A 2009 Commun. Comput. Phys. 5 84
[7] 王同科 2010 数值计算和计算机应用 31 64
Wang T K 2010 J. Numerical Methods & Computer Applications 31 64
[8] Safjan A, Oden J 1993 Comput. Methods Appl. Mech. Eng. 103 187
Google Scholar
[9] Cockburn B, Shu C W 1997 SIAM J. Numer. Anal. 35 2440
[10] 赵国忠, 蔚喜军 2012 61 110208
Google Scholar
Zhao G Z, Yu X J 2012 Acta Phys. Sin. 61 110208
Google Scholar
[11] Chung E, Engquist B 2009 SIAM J. Numer. Anal. 47 3820
Google Scholar
[12] Chou C S, Shu C W, Xing Y 2014 J. Comput. Phys. 272 88
Google Scholar
[13] Nie Q, Zhang Y T, Zhao R 2006 J. Comput. Phys. 214 521
Google Scholar
[14] 张荣培, 王震, 王语, 韩子健 2018 67 050503
Google Scholar
Zhang R P, Wang Z, Wang Y, Han Z J 2018 Acta Phys. Sin. 67 050503
Google Scholar
[15] Wang Y, Zhang R P, Wang Z J, Han Z 2019 Chin. Phys. B 28 50503
Google Scholar
[16] Chen S, Zhang Y 2011 J. Comput. Phys. 230 4336
Google Scholar
-
图 1 (a)算例2的网格剖分和数值解
${w_h}$ 在不同时刻(b)$t = 0.2$ , (c)$t = 0.{\rm{3}}$ , (d)$t = 0.{\rm{4}}$ 时的波传播Figure 1. (a) The triangulation mesh of Example 2; contour plot of solution
${w_h}$ at different time: (b)$t = 0.2$ ; (c)$t = 0.{\rm{3}}$ ; (d)$t = 0.{\rm{4}}$ .
图 2 算例2的能量随时间的演化
Figure 2. Energy evolution with time for Example 2.
图 3 (a)算例3的网格剖分和数值解
${w_h}$ 在不同时刻 (b)$t = 0.{\rm{1}}$ , (c)$t = 0.{\rm{3}}$ , (d)$t = 0.{\rm{45}}$ 时的波传播Figure 3. (a) The triangulation mesh of Example 3; contour plot of solution
${w_h}$ at different time: (b)$t = 0.{\rm{1}}$ ; (c)$t = 0.{\rm{3}}$ ; (d)$t = 0.{\rm{45}}$ .表 1 数值解
${w_h}$ 和p的误差和收敛阶数Table 1. Error and convergence order of numerical solution
${w_h}$ and p.网格数 w的误差 p的误差 ${L^2}$范数下误差 收敛阶 ${L^2}$范数下误差 收敛阶 $8 \times 8$ 2.80 × 10–2 — 6.63× 10–2 — $16 \times 16$ 5.75 × 10–3 2.28 3.40× 10–2 0.96 $32 \times 32$ 1.64 × 10–3 1.81 1.70× 10–2 1.00 $64 \times 64$ 4.62 × 10–4 1.83 8.56× 10–3 0.99 $128 \times 128$ 9.20 × 10–5 2.32 4.30 × 10–3 0.99 
DownLoad: CSV
-
[1] 周聪, 王庆良 2015 64 239101
Google Scholar
Zhou C, Wang Q L 2015 Acta Phys. Sin. 64 239101
Google Scholar
[2] 王飞, 魏兵, 李林茜 2014 63 104101
Google Scholar
Wang F, Wei B, Li L X 2014 Acta Phys. Sin. 63 104101
Google Scholar
[3] 王婷, 崔志文, 刘金霞, 王克协 2018 67 114301
Google Scholar
Wang T, Cui Z W, Liu J X, Wang K X 2018 Acta Phys. Sin. 67 114301
Google Scholar
[4] Kampanis N A, Ekaterinaris J, Dougalis V 2008 Effective Computational Methods for Wave Propagation (Virginia beach: Chapman & Hall/CRC) pp135−164
[5] Sjögreen B, Anders P N 2011 J. Sci. Comput. 52 17
[6] Appelö D, Petersson N A 2009 Commun. Comput. Phys. 5 84
[7] 王同科 2010 数值计算和计算机应用 31 64
Wang T K 2010 J. Numerical Methods & Computer Applications 31 64
[8] Safjan A, Oden J 1993 Comput. Methods Appl. Mech. Eng. 103 187
Google Scholar
[9] Cockburn B, Shu C W 1997 SIAM J. Numer. Anal. 35 2440
[10] 赵国忠, 蔚喜军 2012 61 110208
Google Scholar
Zhao G Z, Yu X J 2012 Acta Phys. Sin. 61 110208
Google Scholar
[11] Chung E, Engquist B 2009 SIAM J. Numer. Anal. 47 3820
Google Scholar
[12] Chou C S, Shu C W, Xing Y 2014 J. Comput. Phys. 272 88
Google Scholar
[13] Nie Q, Zhang Y T, Zhao R 2006 J. Comput. Phys. 214 521
Google Scholar
[14] 张荣培, 王震, 王语, 韩子健 2018 67 050503
Google Scholar
Zhang R P, Wang Z, Wang Y, Han Z J 2018 Acta Phys. Sin. 67 050503
Google Scholar
[15] Wang Y, Zhang R P, Wang Z J, Han Z 2019 Chin. Phys. B 28 50503
Google Scholar
[16] Chen S, Zhang Y 2011 J. Comput. Phys. 230 4336
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7900
- PDF Downloads: 82
- Cited By: 0
