Interpolating element-free Galerkin method for viscoelasticity problems

Zhang Peng-Xuan; Peng Miao-Juan

doi:10.7498/aps.68.20191047

Abstract

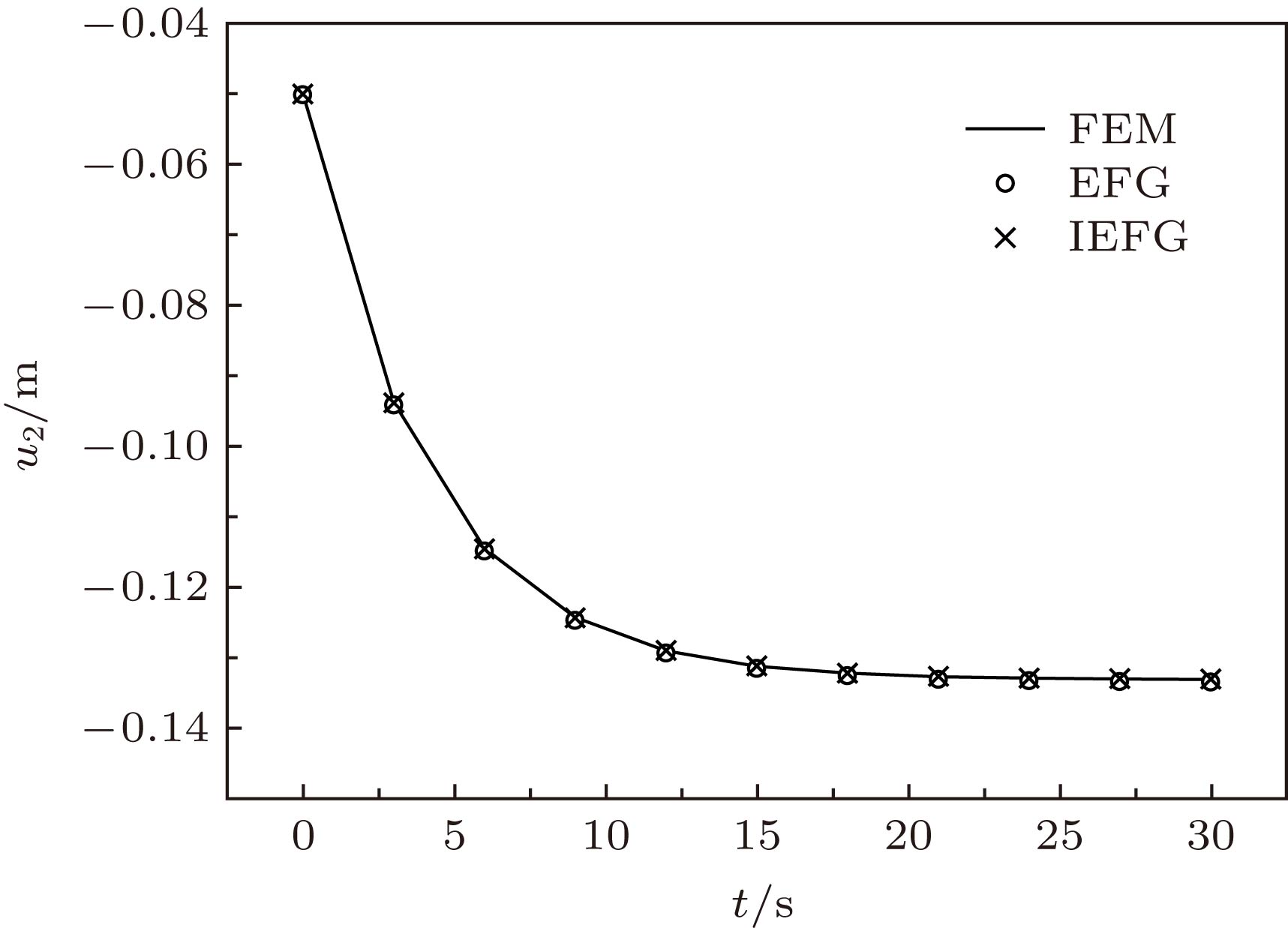
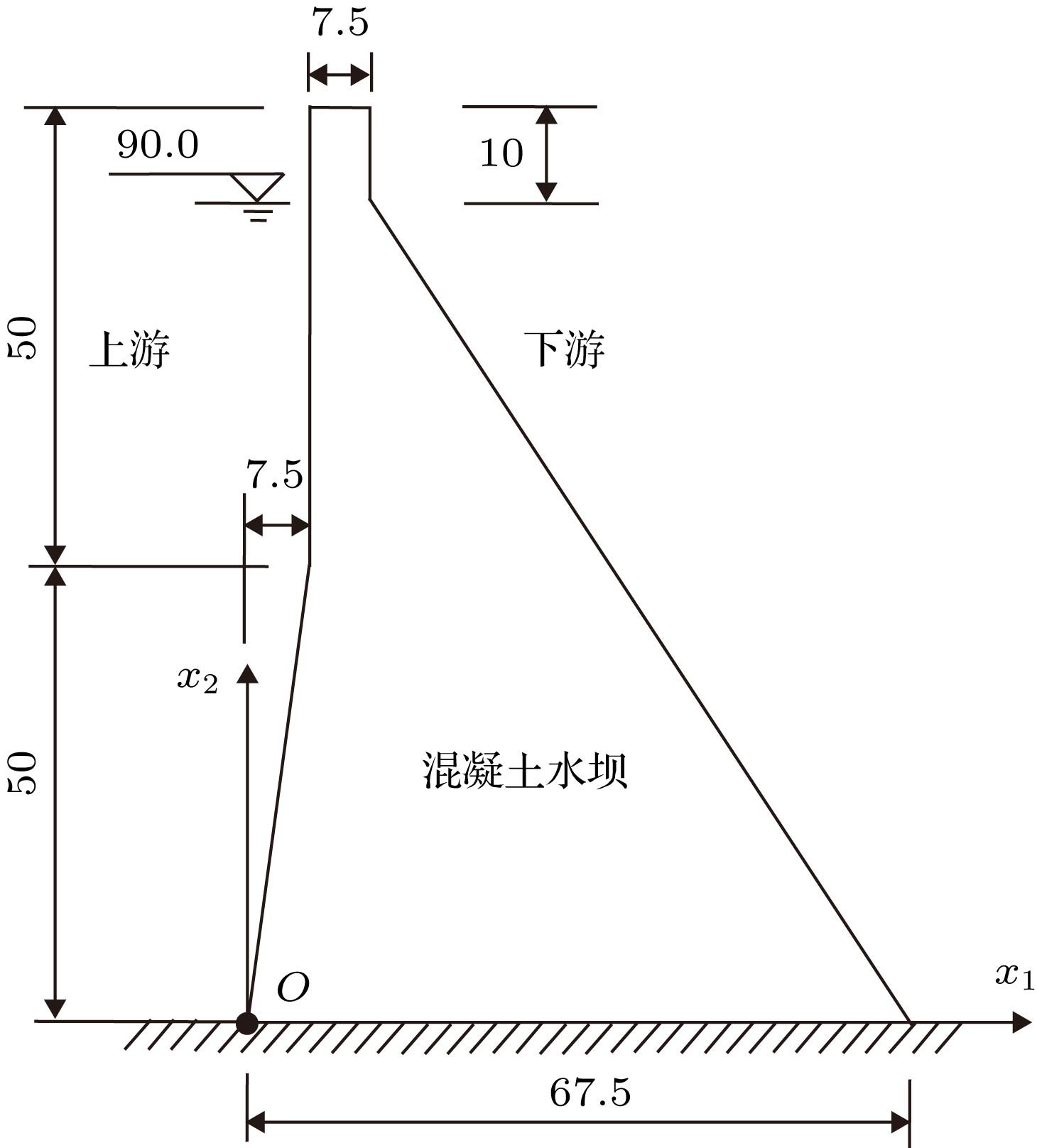
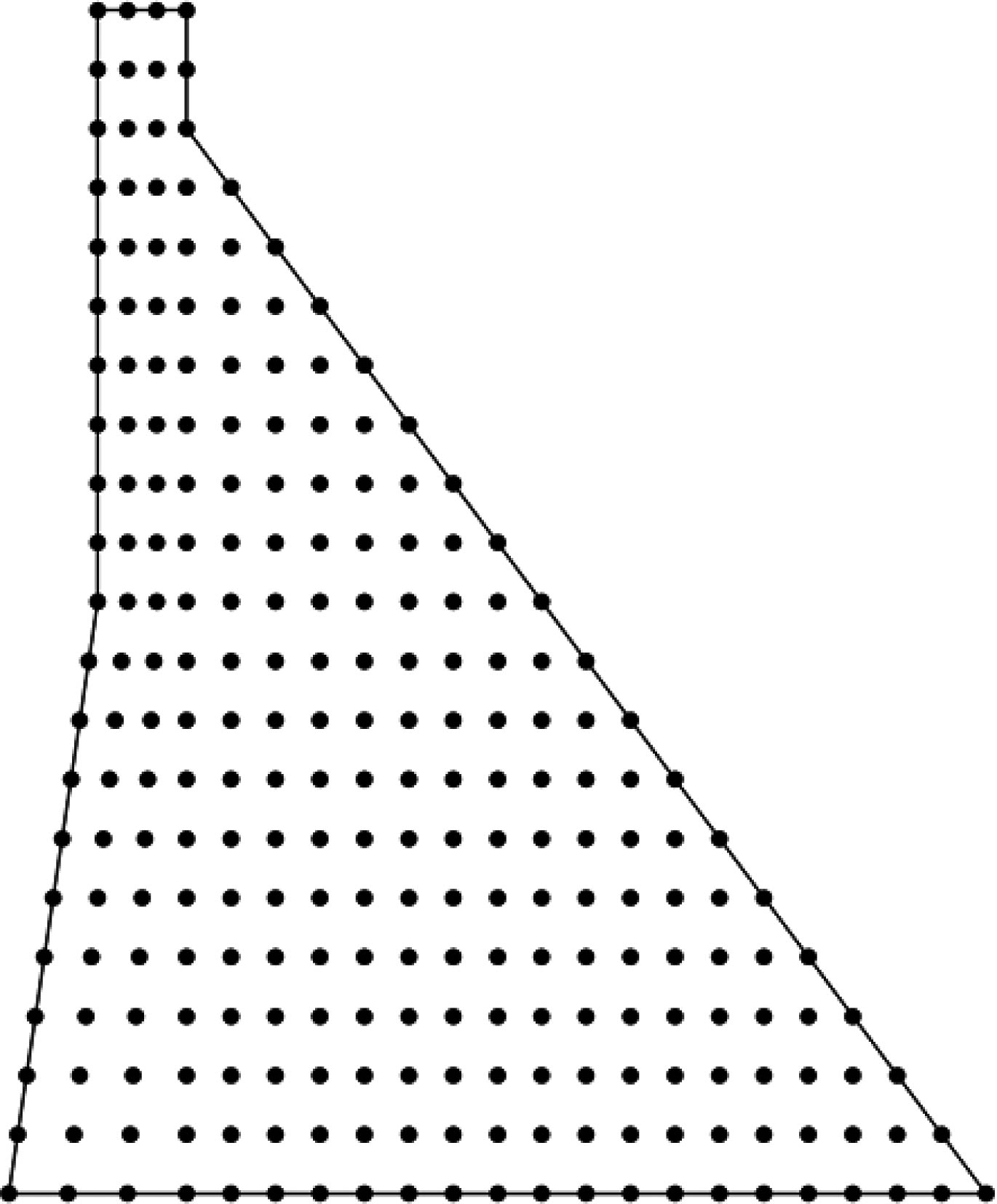
In this paper, based on the improved interpolating moving least-square (IMLS) approximation, the interpolating element-free Galerkin (IEFG) method for two-dimensional viscoelasticity problems is presented. The shape function constructed by the IMLS approximation can overcome the shortcomings that the shape function of the moving least-squares (MLS) can-not satisfy the property of Kronecker function, so the essential boundary conditions can be directly applied to the IEFG method. Under a similar computational precision, compared with the meshless method based on the MLS approximation, the meshless method using the IMLS approximation has a high computational efficiency. Using the IMLS approximation to form the shape function and adopting the Galerkin weak form of the two-dimensional viscoelasticity problem to obtain the final discretized equation, the formulae for two-dimensional viscoelasticity problem are derived by the IEFG method. The IEFG method has some advantages over the conventional element-free Galerkin (EFG) method, such as the concise formulae and direct application of the essential boundary conditions, For the IEFG method of two-dimensional viscoelasticity problems proposed in this paper, three numerical examples and one engineering example are given. The convergence of the method is analyzed by considering the effects of the scale parameters of influence domains and the node distribution on the computational precision of the solutions. It is shown that when d_max = 1.01−2.00, the method in this paper has a good convergence. The numerical results from the IEFG method are compared with those from the EFG method and from the finite element method or analytical solution. We can see that the IEFG method in this paper is effective. The results of the examples show that the IEFG method has the advantage in improving the computational efficiency of the EFG method under a similar computational accuracy. And the engineering example shows that the IEFG method can not only has higher computational precision, but also improve the computational efficiency.

Keywords:

Authors and contacts

Department of Civil Engineering, Shanghai University, Shanghai 200444, China

Corresponding author: Peng Miao-Juan, mjpeng@shu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11571223)

FullText HTML : translate this paragraph

References

[1]	程玉民 2015 无网格方法 (北京: 科学出版社) 第1−13 页 Cheng Y M 2015 Meshless Methods (Beijing: Science Press) pp1−13 (in Chinese)
[2]	程荣军, 程玉民 2008 57 6037 Google Scholar Cheng R J, Cheng Y M 2008 Acta Phys. Sin. 57 6037 Google Scholar
[3]	Cheng Y M, Wang J F, Li R X 2012 Int. J. Appl. Mech. 4 1250042 Google Scholar
[4]	Chen L, Cheng Y M, Ma H P 2015 Comput. Mech. 55 591 Google Scholar
[5]	Chen L, Cheng Y M 2018 Comput. Mech. 62 67 Google Scholar
[6]	Chen L, Cheng Y M 2010 Chin. Phys. B 19 090204 Google Scholar
[7]	Cheng R J, Cheng Y M 2008 Appl. Numer. Math. 58 884 Google Scholar
[8]	Chen L, Liu C, Ma H P, et al. 2014 Int. J. Appl. Mech. 6 1450009 Google Scholar
[9]	李树忱, 程玉民 2004 力学学报 36 496 Google Scholar Li S C, Cheng Y M 2004 Acta Mech. Sin. 36 496 Google Scholar
[10]	Gao H F, Cheng Y M 2010 Int. J. Comput. Meth. 7 55 Google Scholar
[11]	程玉民, 李九红 2005 54 4463 Google Scholar Cheng Y M, Li J H 2005 Acta Phys. Sin. 54 4463 Google Scholar
[12]	Cheng Y M, Li J H 2006 Sci. China Ser. G 49 46
[13]	程玉民, 彭妙娟, 李九红 2005 力学学报 37 719 Google Scholar Cheng Y M, Peng M J, Li J H 2005 Acta Mech. Sin. 37 719 Google Scholar
[14]	Bai F N, Li D M, Wang J F, Cheng Y M 2012 Chin. Phys. B 21 020204 Google Scholar
[15]	Cheng Y M, Wang J F, Bai F N 2012 Chin. Phys. B 21 090203 Google Scholar
[16]	Cheng H, Peng M J, Cheng Y M 2017 Eng. Anal. Boundary Elem. 84 52 Google Scholar
[17]	Cheng H, Peng M J, Cheng Y M 2017 Int. J. Appl. Mech. 9 1750090 Google Scholar
[18]	Cheng H, Peng M J, Cheng Y M 2018 Int. J. Numer. Methods Eng. 114 321 Google Scholar
[19]	Cheng H, Peng M J, Cheng Y M 2018 Eng. Anal. Boundary Elem. 97 39 Google Scholar
[20]	程玉民, 陈美娟 2003 力学学报 35 181 Google Scholar Cheng Y M, Chen M J 2003 Acta Mech. Sin. 35 181 Google Scholar
[21]	Cheng Y M, Peng M J 2005 Sci. China Ser. G 48 641
[22]	秦义校, 程玉民 2006 55 3215 Google Scholar Qin Y X, Cheng Y M 2006 Acta Phys. Sin. 55 3215 Google Scholar
[23]	Peng M J, Cheng Y M 2009 Eng. Anal. Boundary Elem. 33 77 Google Scholar
[24]	Ren H P, Cheng Y M, Zhang W 2009 Chin. Phys. B 18 4065 Google Scholar
[25]	Ren H P, Cheng Y M, Zhang W 2010 Sci. China Ser. G 53 758 Google Scholar
[26]	Wang J F, Wang J F, Sun F X, Cheng Y M 2013 Int. J. Comput. Methods 10 1350043 Google Scholar
[27]	Zhang Z, Li D M, Cheng Y M, et al. 2012 Acta Mech. Sin. 28 808 Google Scholar
[28]	Zhang Z, Hao S Y, Liew K M, et al. 2013 Eng. Anal. Boundary Elem. 37 1576 Google Scholar
[29]	Zhang Z, Wang J F, Cheng Y M, et al. 2013 Sci. China Ser. G 56 1568 Google Scholar
[30]	Cheng R J, Liew K M 2012 Eng. Anal. Boundary Elem. 36 1322 Google Scholar
[31]	Cheng R J, Wei Q 2013 Chin. Phys. B 22 060209 Google Scholar
[32]	Peng M J, Li R X, Cheng Y M 2014 Eng. Anal. Boundary Elem. 40 104 Google Scholar
[33]	蔡小杰, 彭妙娟, 程玉民 2018 中国科学: 物理学力学天文学 48 024701 Google Scholar Cai X J, Peng M J, Cheng Y M 2018 Sci. China: Phys. Mech. Astron. 48 024701 Google Scholar
[34]	Yu S Y, Peng M J, Cheng H, Cheng Y M 2019 Eng. Anal. Boundary Elem. 104 215 Google Scholar
[35]	邹诗莹, 席伟成, 彭妙娟, 程玉民 2017 66 120204 Google Scholar Zou S Y, Xi W C, Peng M J, Cheng Y M 2017 Acta Phys. Sin. 66 120204 Google Scholar
[36]	Wu Y, Ma Y Q, Feng W, Cheng Y M 2017 Chin. Phys. B 26 080203 Google Scholar
[37]	Meng Z J, Cheng H, Ma L D, Cheng Y M 2018 Acta Mech. Sin. 34 462 Google Scholar
[38]	Meng Z J, Cheng H, Ma L D, Cheng Y M 2019 Sci. China Ser. G 62 040711 Google Scholar
[39]	Meng Z J, Cheng H, Ma L D, Cheng Y M 2019 Int. J. Numer. Methods Eng. 117 15 Google Scholar
[40]	Lancaster P, Salkauskas K 1981 Math. Comput. 37 141 Google Scholar
[41]	Ren H P, Cheng Y M 2011 Int. J. Appl. Mech. 3 735 Google Scholar
[42]	Ren H P, Cheng Y M 2012 Eng. Anal. Boundary Elem. 36 873 Google Scholar
[43]	Cheng Y M, Bai F N, Peng M J 2014 Appl. Math. Model. 38 5187 Google Scholar
[44]	Cheng Y M, Bai F N, Liu C, Peng M J 2016 Int. J. Comput. Mater. Sci. Eng. 5 1650023
[45]	Deng Y J, Liu C, Peng M J, Cheng Y M 2015 Int. J. Appl. Mech. 7 1550017 Google Scholar
[46]	Wang J F, Sun F X, Cheng Y M 2012 Chin. Phys. B 21 090204 Google Scholar
[47]	Sun F X, Wang J F, Cheng Y M 2013 Chin. Phys. B 22 120203 Google Scholar
[48]	Sun F X, Wang J F, Cheng Y M 2016 Int. J. Appl. Mech. 8 1650096 Google Scholar
[49]	Wang J F, Hao S Y, Cheng Y M 2014 Math. Probl. Eng. 2014 641592
[50]	Wang J F, Sun F X, Cheng Y M, Huang A X 2014 Appl. Math. Comput. 245 321
[51]	Sun F X, Wang J F, Cheng Y M 2015 Appl. Numer. Math. 98 79 Google Scholar
[52]	Liu F B, Cheng Y M 2018 Int. J. Comput. Mater. Sci. Eng. 7 1850023
[53]	Liu F B, Cheng Y M 2018 Int. J. Appl. Mech. 10 1850047 Google Scholar
[54]	Liu F B, Wu Q, Cheng Y M 2019 Int. J. Appl. Mech. 11 1950006 Google Scholar
[55]	Yang H T, Liu Y 2003 Int. J. Solids Struct. 40 701 Google Scholar
[56]	Canelas A, Sensale B 2010 Eng. Anal. Boundary Elem. 34 845 Google Scholar
[57]	Cheng Y M, Li R X, Peng M J 2012 Chin. Phys. B 21 090205 Google Scholar
[58]	彭妙娟, 刘茜 2014 63 180203 Google Scholar Peng M J, Liu Q 2014 Acta Phys. Sin. 63 180203 Google Scholar

Cited By

图 1 受均布荷载的悬臂梁

Figure 1. A cantilever beam subjected to a distributed loading

DownLoad: Full-Size Img PowerPoint

图 2 不同节点分布下有限元法解的方差

Figure 2. The variances of the solutions of FEM under different node distributions.

DownLoad: Full-Size Img PowerPoint

图 3 不同节点分布下的相对误差

Figure 3. The relative error under different node distributions.

DownLoad: Full-Size Img PowerPoint

图 4 节点布置

Figure 4. Node distribution.

DownLoad: Full-Size Img PowerPoint

图 5 不同影响域比例参数下的相对误差

Figure 5. The relative error for different scale parameters of influence domains.

DownLoad: Full-Size Img PowerPoint

图 6 $t = 20 \;{\rm{s}}$时悬臂梁中轴线上各点的挠度

Figure 6. Vertical displacements of nodes on the neutral axis of the beam when $t = 20 \;{\rm{s}}$.

DownLoad: Full-Size Img PowerPoint

图 7 梁右端中点的挠度随时间的变化

Figure 7. Time history of vertical displacement of midpoint in the right end of the beam.

DownLoad: Full-Size Img PowerPoint

图 8 纯弯曲的梁

Figure 8. A beam subjected to simple bending

DownLoad: Full-Size Img PowerPoint

图 9 节点分布

Figure 9. Node distribution.

DownLoad: Full-Size Img PowerPoint

图 10 $t = 30 \;{\rm{s}}$时梁中轴线上的节点挠度

Figure 10. Vertical displacements of nodes on the neutral axis of the beam when $t = 30 \;{\rm{s}}$.

DownLoad: Full-Size Img PowerPoint

图 11 梁右端中点的挠度随时间$t$的变化

Figure 11. Time history of vertical displacement of midpoint in the right end of the beam.

DownLoad: Full-Size Img PowerPoint

图 12 受均布内压的厚壁圆筒

Figure 12. Circular ring under a distributed inner pressure

DownLoad: Full-Size Img PowerPoint

图 13 受均布内压1/4圆筒

Figure 13. A quarter of the circular ring under a distributed inner pressure

DownLoad: Full-Size Img PowerPoint

图 14 1/4圆筒的节点分布

Figure 14. Node distribution of a quarter of the circular ring.

DownLoad: Full-Size Img PowerPoint

图 15 $t = 30 \;{\rm{s}}$时沿${x_2} = {\rm{0}}$线上节点的位移

Figure 15. Radial displacements at${x_2} = {\rm{0}}$ when $t = 30 \;{\rm{s}}$.

DownLoad: Full-Size Img PowerPoint

图 16 点$(2,0)$的径向位移随时间$t$的变化

Figure 16. Time history of radial displacement at point $(2,0)$.

DownLoad: Full-Size Img PowerPoint

图 17 受静水压力的混凝土水坝

Figure 17. A concrete dam under hydrostatic pressure.

DownLoad: Full-Size Img PowerPoint

图 18 混凝土水坝的节点分布

Figure 18. Node distribution of a concrete dam.

DownLoad: Full-Size Img PowerPoint

图 19 $t = 500$ d时沿${x_1} = 15$方向上节点的水平位移

Figure 19. Horizontal displacements at ${x_1} = 15$ when $t = 500\; {\rm d}$.

DownLoad: Full-Size Img PowerPoint

图 20 混凝土坝上点$(15, 50)$的水平位移与时间的关系

Figure 20. Time history of horizontal displacement of the point $(15, 50)$.

DownLoad: Full-Size Img PowerPoint

map

[1]	程玉民 2015 无网格方法 (北京: 科学出版社) 第1−13 页 Cheng Y M 2015 Meshless Methods (Beijing: Science Press) pp1−13 (in Chinese)
[2]	程荣军, 程玉民 2008 57 6037 Google Scholar Cheng R J, Cheng Y M 2008 Acta Phys. Sin. 57 6037 Google Scholar
[3]	Cheng Y M, Wang J F, Li R X 2012 Int. J. Appl. Mech. 4 1250042 Google Scholar
[4]	Chen L, Cheng Y M, Ma H P 2015 Comput. Mech. 55 591 Google Scholar
[5]	Chen L, Cheng Y M 2018 Comput. Mech. 62 67 Google Scholar
[6]	Chen L, Cheng Y M 2010 Chin. Phys. B 19 090204 Google Scholar
[7]	Cheng R J, Cheng Y M 2008 Appl. Numer. Math. 58 884 Google Scholar
[8]	Chen L, Liu C, Ma H P, et al. 2014 Int. J. Appl. Mech. 6 1450009 Google Scholar
[9]	李树忱, 程玉民 2004 力学学报 36 496 Google Scholar Li S C, Cheng Y M 2004 Acta Mech. Sin. 36 496 Google Scholar
[10]	Gao H F, Cheng Y M 2010 Int. J. Comput. Meth. 7 55 Google Scholar
[11]	程玉民, 李九红 2005 54 4463 Google Scholar Cheng Y M, Li J H 2005 Acta Phys. Sin. 54 4463 Google Scholar
[12]	Cheng Y M, Li J H 2006 Sci. China Ser. G 49 46
[13]	程玉民, 彭妙娟, 李九红 2005 力学学报 37 719 Google Scholar Cheng Y M, Peng M J, Li J H 2005 Acta Mech. Sin. 37 719 Google Scholar
[14]	Bai F N, Li D M, Wang J F, Cheng Y M 2012 Chin. Phys. B 21 020204 Google Scholar
[15]	Cheng Y M, Wang J F, Bai F N 2012 Chin. Phys. B 21 090203 Google Scholar
[16]	Cheng H, Peng M J, Cheng Y M 2017 Eng. Anal. Boundary Elem. 84 52 Google Scholar
[17]	Cheng H, Peng M J, Cheng Y M 2017 Int. J. Appl. Mech. 9 1750090 Google Scholar
[18]	Cheng H, Peng M J, Cheng Y M 2018 Int. J. Numer. Methods Eng. 114 321 Google Scholar
[19]	Cheng H, Peng M J, Cheng Y M 2018 Eng. Anal. Boundary Elem. 97 39 Google Scholar
[20]	程玉民, 陈美娟 2003 力学学报 35 181 Google Scholar Cheng Y M, Chen M J 2003 Acta Mech. Sin. 35 181 Google Scholar
[21]	Cheng Y M, Peng M J 2005 Sci. China Ser. G 48 641
[22]	秦义校, 程玉民 2006 55 3215 Google Scholar Qin Y X, Cheng Y M 2006 Acta Phys. Sin. 55 3215 Google Scholar
[23]	Peng M J, Cheng Y M 2009 Eng. Anal. Boundary Elem. 33 77 Google Scholar
[24]	Ren H P, Cheng Y M, Zhang W 2009 Chin. Phys. B 18 4065 Google Scholar
[25]	Ren H P, Cheng Y M, Zhang W 2010 Sci. China Ser. G 53 758 Google Scholar
[26]	Wang J F, Wang J F, Sun F X, Cheng Y M 2013 Int. J. Comput. Methods 10 1350043 Google Scholar
[27]	Zhang Z, Li D M, Cheng Y M, et al. 2012 Acta Mech. Sin. 28 808 Google Scholar
[28]	Zhang Z, Hao S Y, Liew K M, et al. 2013 Eng. Anal. Boundary Elem. 37 1576 Google Scholar
[29]	Zhang Z, Wang J F, Cheng Y M, et al. 2013 Sci. China Ser. G 56 1568 Google Scholar
[30]	Cheng R J, Liew K M 2012 Eng. Anal. Boundary Elem. 36 1322 Google Scholar
[31]	Cheng R J, Wei Q 2013 Chin. Phys. B 22 060209 Google Scholar
[32]	Peng M J, Li R X, Cheng Y M 2014 Eng. Anal. Boundary Elem. 40 104 Google Scholar
[33]	蔡小杰, 彭妙娟, 程玉民 2018 中国科学: 物理学力学天文学 48 024701 Google Scholar Cai X J, Peng M J, Cheng Y M 2018 Sci. China: Phys. Mech. Astron. 48 024701 Google Scholar
[34]	Yu S Y, Peng M J, Cheng H, Cheng Y M 2019 Eng. Anal. Boundary Elem. 104 215 Google Scholar
[35]	邹诗莹, 席伟成, 彭妙娟, 程玉民 2017 66 120204 Google Scholar Zou S Y, Xi W C, Peng M J, Cheng Y M 2017 Acta Phys. Sin. 66 120204 Google Scholar
[36]	Wu Y, Ma Y Q, Feng W, Cheng Y M 2017 Chin. Phys. B 26 080203 Google Scholar
[37]	Meng Z J, Cheng H, Ma L D, Cheng Y M 2018 Acta Mech. Sin. 34 462 Google Scholar
[38]	Meng Z J, Cheng H, Ma L D, Cheng Y M 2019 Sci. China Ser. G 62 040711 Google Scholar
[39]	Meng Z J, Cheng H, Ma L D, Cheng Y M 2019 Int. J. Numer. Methods Eng. 117 15 Google Scholar
[40]	Lancaster P, Salkauskas K 1981 Math. Comput. 37 141 Google Scholar
[41]	Ren H P, Cheng Y M 2011 Int. J. Appl. Mech. 3 735 Google Scholar
[42]	Ren H P, Cheng Y M 2012 Eng. Anal. Boundary Elem. 36 873 Google Scholar
[43]	Cheng Y M, Bai F N, Peng M J 2014 Appl. Math. Model. 38 5187 Google Scholar
[44]	Cheng Y M, Bai F N, Liu C, Peng M J 2016 Int. J. Comput. Mater. Sci. Eng. 5 1650023
[45]	Deng Y J, Liu C, Peng M J, Cheng Y M 2015 Int. J. Appl. Mech. 7 1550017 Google Scholar
[46]	Wang J F, Sun F X, Cheng Y M 2012 Chin. Phys. B 21 090204 Google Scholar
[47]	Sun F X, Wang J F, Cheng Y M 2013 Chin. Phys. B 22 120203 Google Scholar
[48]	Sun F X, Wang J F, Cheng Y M 2016 Int. J. Appl. Mech. 8 1650096 Google Scholar
[49]	Wang J F, Hao S Y, Cheng Y M 2014 Math. Probl. Eng. 2014 641592
[50]	Wang J F, Sun F X, Cheng Y M, Huang A X 2014 Appl. Math. Comput. 245 321
[51]	Sun F X, Wang J F, Cheng Y M 2015 Appl. Numer. Math. 98 79 Google Scholar
[52]	Liu F B, Cheng Y M 2018 Int. J. Comput. Mater. Sci. Eng. 7 1850023
[53]	Liu F B, Cheng Y M 2018 Int. J. Appl. Mech. 10 1850047 Google Scholar
[54]	Liu F B, Wu Q, Cheng Y M 2019 Int. J. Appl. Mech. 11 1950006 Google Scholar
[55]	Yang H T, Liu Y 2003 Int. J. Solids Struct. 40 701 Google Scholar
[56]	Canelas A, Sensale B 2010 Eng. Anal. Boundary Elem. 34 845 Google Scholar
[57]	Cheng Y M, Li R X, Peng M J 2012 Chin. Phys. B 21 090205 Google Scholar
[58]	彭妙娟, 刘茜 2014 63 180203 Google Scholar Peng M J, Liu Q 2014 Acta Phys. Sin. 63 180203 Google Scholar

[1]	Zhou Hao, Li Yi, Liu Hai, Chen Hong, Ren Lei-Sheng. Optimized transportation meshfree method and its apllication in simulating droplet surface tension effect. Acta Physica Sinica, 2021, 70(24): 240203. doi: 10.7498/aps.70.20211078
[2]	Zou Shi-Ying, Xi Wei-Cheng, Peng Miao-Juan, Cheng Yu-Min. Analysis of fracture problems of airport pavement by improved element-free Galerkin method. Acta Physica Sinica, 2017, 66(12): 120204. doi: 10.7498/aps.66.120204
[3]	Du Chao-Fan, Zhang Ding-Guo. A meshfree method based on point interpolation for dynamic analysis of rotating cantilever beams. Acta Physica Sinica, 2015, 64(3): 034501. doi: 10.7498/aps.64.034501
[4]	Du Hong-Xiu, Wei Hong, Qin Yi-Xiao, Li Zhong-Hua, Wang Tong-Zun. Interpolating particle method for mechanical analysis of space axisymmetric components. Acta Physica Sinica, 2015, 64(10): 100204. doi: 10.7498/aps.64.100204
[5]	Fan Ji-Hua, Zhang Ding-Guo. Bezier interpolation method for the dynamics of rotating flexible cantilever beam. Acta Physica Sinica, 2014, 63(15): 154501. doi: 10.7498/aps.63.154501
[6]	Peng Miao-Juan, Liu Qian. Improved complex variable element-free Galerkin method for viscoelasticity problems. Acta Physica Sinica, 2014, 63(18): 180203. doi: 10.7498/aps.63.180203
[7]	Feng Zhao, Wang Xiao-Dong, Ouyang Jie. The element-free Galerkin method based on the shifted basis for solving the Kuramoto- Sivashinsky equation. Acta Physica Sinica, 2012, 61(23): 230204. doi: 10.7498/aps.61.230204
[8]	Yang Xiu-Li, Dai Bao-Dong, Li Zhen-Feng. Meshless local Petrov-Galerkin method with complex variables for elasticity. Acta Physica Sinica, 2012, 61(5): 050204. doi: 10.7498/aps.61.050204
[9]	Li Zhong-Hua, Qin Yi-Xiao, Cui Xiao-Chao. Interpolating reproducing kernel particle method for elastic mechanics. Acta Physica Sinica, 2012, 61(8): 080205. doi: 10.7498/aps.61.080205
[10]	Cheng Yu-Min, Cheng Rong-Jun. Error estimate of element-free Galerkin method for elasticity. Acta Physica Sinica, 2011, 60(7): 070206. doi: 10.7498/aps.60.070206
[11]	Zheng Bao-Jing, Dai Bao-Dong. Improved meshless local Petrov-Galerkin method for two-dimensional potential problems. Acta Physica Sinica, 2010, 59(8): 5182-5189. doi: 10.7498/aps.59.5182
[12]	Li Jun, Dong Hai-Ying. Modelling of chaotic systems using wavelet kernel partial least squares regression method. Acta Physica Sinica, 2008, 57(8): 4756-4765. doi: 10.7498/aps.57.4756
[13]	Tang Bo, Li Jun-Feng, Wang Tian-Shu. Numerical simulation of liquid drop phenomenon by least square particle finite element method. Acta Physica Sinica, 2008, 57(11): 6722-6729. doi: 10.7498/aps.57.6722
[14]	Chen Li, Cheng Yu-Min. Reproducing kernel particle method with complex variables for elasticity. Acta Physica Sinica, 2008, 57(1): 1-10. doi: 10.7498/aps.57.1
[15]	Cheng Rong-Jun, Cheng Yu-Min. Error estimates of element-free Galerkin method for potential problems. Acta Physica Sinica, 2008, 57(10): 6037-6046. doi: 10.7498/aps.57.6037
[16]	Dai Bao-Dong, Cheng Yu-Min. Local boundary integral equation method based on radial basis functions for potential problems. Acta Physica Sinica, 2007, 56(2): 597-603. doi: 10.7498/aps.56.597
[17]	Cheng Rong-Jun, Cheng Yu-Min. The meshless method for solving the inverse heat conduction problem with a source parameter. Acta Physica Sinica, 2007, 56(10): 5569-5574. doi: 10.7498/aps.56.5569
[18]	Qin Yi-Xiao, Cheng Yu-Min. Reproducing kernel particle boundary element-free method for elasticity. Acta Physica Sinica, 2006, 55(7): 3215-3222. doi: 10.7498/aps.55.3215
[19]	Li Shu-Chen, Cheng Yu-Min, Li Shu-Cai. Meshless manifold method for dynamic fracture mechanics. Acta Physica Sinica, 2006, 55(9): 4760-4766. doi: 10.7498/aps.55.4760
[20]	Cheng Yu-Min, Li Jiu-Hong. A meshless method with complex variables for elasticity. Acta Physica Sinica, 2005, 54(10): 4463-4471. doi: 10.7498/aps.54.4463

Catalog

Vol. 68, Issue 17 - 2019-09-05

Metrics

Abstract views: 7223
PDF Downloads: 44
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板