-
Vibration noise has an influence on the sensitivity and stability for many precision instruments, especially for atom interferometers. In this paper, a mobile three-dimensional active vibration isolation system is established for portable atom interferometer that is effectively isolated from the ground vibration, thereby improving the sensitivity of the portable atom interferometer, and can be deployed and recovered to working state rapidly. With the home-developed integrated feedback algorithm, this system achieves a good vibration suppression in a wide frequency range in three directions. It suppresses the ground vibration by three orders of magnitude in the vertical direction, and one order of magnitude in the horizontal direction. In a frequency range less than 10 Hz which the atom interferometer is sensitive to, the vibration noise is suppressed to 4.8 × 10–9 m/s2/Hz1/2 in the vertical direction and to 2.7 × 10–7 m/s2/Hz1/2 in the horizontal direction. The influence of vibration noise on the sensitivity of the atom interferometer reaches to 2 μGal/Hz1/2, which is reduced by two orders of magnitude compared with the result without our system.
[1] Abbott B, Abbott R, Abbott T D, Abernathy M R, Acernese F, Ackley K, Adams C, Adams T, Addesso P, Adhikari R 2016 Phys. Rev. Lett. 116 061102
Google Scholar
[2] Abbott B P, Abbott R, Abbott T D, Acernese F, Ackley K, Adams C, Adams T, Addesso P, Adhikari R X, Adya V B 2017 Astrophys. J. 851 1
Google Scholar
[3] Matichard F, Lantz B, Mason K, Mittleman R, Abbott B, Abbott S, Allwine E, Barnum S, Birch J, Biscans S 2015 Precis. Eng. 40 273
Google Scholar
[4] Campbell S L, Hutson R, Marti G E, Goban A, Oppong N D, Mcnally R L, Sonderhouse L, Robinson J M, Zhang W, Bloom B 2017 Science 358 90
Google Scholar
[5] Ludlow A D, Boyd M M, Ye J, Peik E, Schmidt P O 2015 Rev. Mod. Phys. 87 637
Google Scholar
[6] Chen L, Hall J L, Ye J, Yang T, Zang E, Li T 2006 Phys. Rev. A 74 053801
Google Scholar
[7] Li Q, Xue C, Liu J, Wu J, Yang S, Shao C, Quan L, Tan W, Tu L, Liu Q 2018 Nature 560 582
Google Scholar
[8] Li Q, Liu J P, Xue C, Wu J F, Yang S Q, Luo J 2016 Rev. Sci. Instrum. 87 351
[9] Jones L, Wang S, Hu X, Rahman S, Castell M R 2018 Adv. Struct. Chem. Imaging 4 7
Google Scholar
[10] Wu X, Zi F, Dudley J, Bilotta R J, Canoza P, Muller H 2017 Optica 4 1545
Google Scholar
[11] Li G, Hu H, Wu K, Wang G, Wang L J 2014 Rev. Sci. Instrum. 85 104502
Google Scholar
[12] Lautier J, Volodimer L, Hardin T, Merlet S, Lours M, Santos F P D, Landragin A 2014 Appl. Phys. Lett. 105 144102
Google Scholar
[13] Hauth M, Freier C, Schkolnik V, Senger A, Schmidt M, Peters A 2013 Phys. Rev. B 113 49
[14] Nelson P G 1991 Rev. Sci. Instrum. 62 2069
Google Scholar
[15] 胡华, 伍康, 申磊, 李刚, 王力军 2012 61 099101
Google Scholar
Hu H, Wu K, Shen L, Li G, Wang L J 2012 Acta Phys. Sin. 61 099101
Google Scholar
[16] Kasevich M A, Chu S 1992 Appl. Phys. B 54 321
Google Scholar
[17] Peters A, Chung K Y, Chu S 2001 Metrologia 38 25
Google Scholar
[18] Dickerson S M, Hogan J M, Sugarbaker A, Johnson D M S, Kasevich M A 2013 Phys. Rev. Lett. 111 083001
Google Scholar
[19] Freier C, Hauth M, Schkolnik V, Keykauf B, Schilling M, Wziontek H, Scherneck H, Muller J, Peters A 2016 J. Phys.: Conf. Ser. 723 012050
Google Scholar
[20] Hu Z K, Sun B L, Duan X C, Zhou M K, Chen L L, Zhan S, Zhang Q Z, Luo J 2013 Phys. Rev. A 88 43610
Google Scholar
[21] Zhang X W, Zhong J Q, Tang B, Chen X, Zhu L, Huang P W, Wang J, Zhan M S 2018 Appl. Opt. 57 6545
Google Scholar
[22] Wang Q, Wang Z, Fu Z, Liu W, Lin Q 2016 Opt. Commun. 358 82
Google Scholar
[23] Wang S K, Zhao Y, Zhuang W, Li T C, Wu S Q, Feng J Y, Li C J 2018 Metrologia 55 360
Google Scholar
[24] Hensley J M, Peters A, Chu S 1999 Rev. Sci. Instrum. 70 2735
Google Scholar
[25] Tang B, Zhou L, Xiong Z Y, Wang J, Zhan M S 2014 Rev. Sci. Instrum. 85 093109
Google Scholar
[26] Zhou M K, Xiong X, Chen L L, Cui J F, Duan X C, Hu Z K 2015 Rev. Sci. Instrum. 86 046108
Google Scholar
[27] Cheinet P, Canuel B, Pereira D S F, Gauguet A, Yverleduc F, Landragin A 2008 IEEE Trans. Instrum. Meas. 57 1141
Google Scholar
-
图 1 三维主动减振系统的结构示意图(地震计测量X, Y, Z三个方向的振动信号输出到低噪声电压放大器进行放大, 再经模数转换器转化为数字信号送入反馈运算器进行综合反馈运算; 得到的反馈信号经数模转换后通过压控电流源驱动音圈电机产生与平台运动方向相反的力从而抑制振动)
Figure 1. Structrue of three-dimension active vibration isolator. Vibration signals measured in the X, Y, Z direction by the seismometer are amplified by a low-noise voltage amplifier, and then converted to digital signals by analog-to-digital converters and sent to a feedback unit for integrated feedback calculation. After passing digital-to-analog converters, the feedback signals drive voice coil actuators by voltage controlled current sources to generate a force opposite to movement direction of the platform to suppress vibration.
图 2 地震计的频率响应曲线(红色实线是理论计算结果, 黑色实点是实验标定的结果) (a)幅频响应; (b)相频响应
Figure 2. Frequency response of the seismometer: (a) Amplitude response; (b) phase response. The red solid line is the theoretical calculation result, and the black solid dot is the experimental measurement result.
图 3 反馈控制算法示意图(
$U_{1}$ ,$U_{2}$ ,$U_{3}$ 分别表示Z, X, Y方向数字化的输入振动信号;$H_{1}$ —$H_{5}$ 表示高通滤波器;$L_{1}$ ,$L_{2}$ 表示低通滤波器;$C_{1}$ ,$C_{2}$ 表示水平耦合系数;$A_{1}$ —$A_{4}$ 表示增益系数;$V_{1}$ ,$V_{2}$ ,$V_{3}$ 分别表示Z, X, Y方向数字化的输出反馈信号)Figure 3. Structure of feedback control algorithm.
$U_{1}$ ,$U_{2}$ ,$U_{3}$ represent the digitized input vibration signals in Z, X and Y directions respectively.$H_{1}$ −$H_{5}$ represent high-pass filters.$C_{1}$ ,$C_{2}$ represent horizontal coupling coefficient.$A_{1}$ −$A_{4}$ represent gain coefficient.$V_{1}$ ,$V_{2}$ ,$V_{3}$ represent the digitized output feedback signals in Z, X and Y directions respectively.
图 4 T = 80 ms时, 振动噪声传递函数(随着振动频率的增大, 传递函数非常迅速地衰减)
Figure 4. Transfor function of the vibration noise (T = 80 ms). The transfer function decays very rapidly as the vibration frequency increases.
图 5 中国科学技术大学上海研究院冷原子干涉仪研究室测试的三维主动减振效果示意图(红色实线为实验室地面上的振动加速度噪声谱, 蓝色实线为被动减振后的结果, 黑色实线为主动减振后的结果)
Figure 5. Performance of the three-dimension active vibration isolator at Shanghai branch, University of Science and Technology of China. The red solid line is the vibration acceleration noise spectrum of the laboratory ground, the bule soild line is the result of the passive isolator, the black solid line is the result of active vibration isolator.
图 6 中国计量院重力精测实验室(II)重力测量点位测试的三维主动减振效果图(红色实线为实验室地面上的振动加速度噪声谱, 蓝色实线为被动减振后的结果, 黑色实线为主动减振后的结果)
Figure 6. Performance of the three-dimension active vibration isolator at Precision Measurement Laboratory II of Gravity, National Institute of Metrology, China. The red solid line is the vibration acceleration noise spectrum of the laboratory ground, the bule soild line is the result of the passive isolator, the black solid line is the result of active vibration isolator.
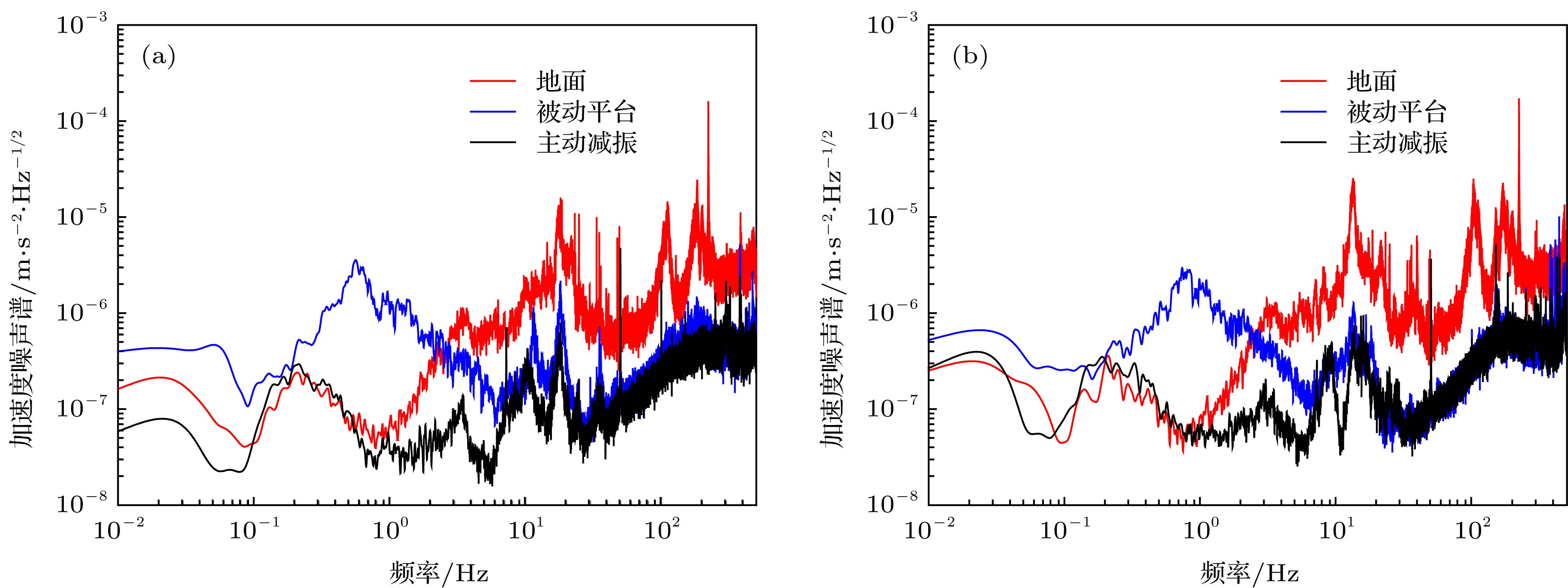
图 7 水平X方向与Y方向的减振效果(红色实线为实验室地面上的振动加速度噪声谱, 蓝色实线为被动减振后的结果, 黑色实线为主动减振后的结果) (a) X方向的减振效果; (b) Y方向的减振效果
Figure 7. Performance of the three-dimension active vibration isolator in X and Y directions: (a) The performance in X direction; (b) the performance in Y direction. The red solid line is the vibration acceleration noise spectrum of the laboratory ground, the bule soild line is the result of the passive isolator, the black solid line is the result of active vibration isolator.
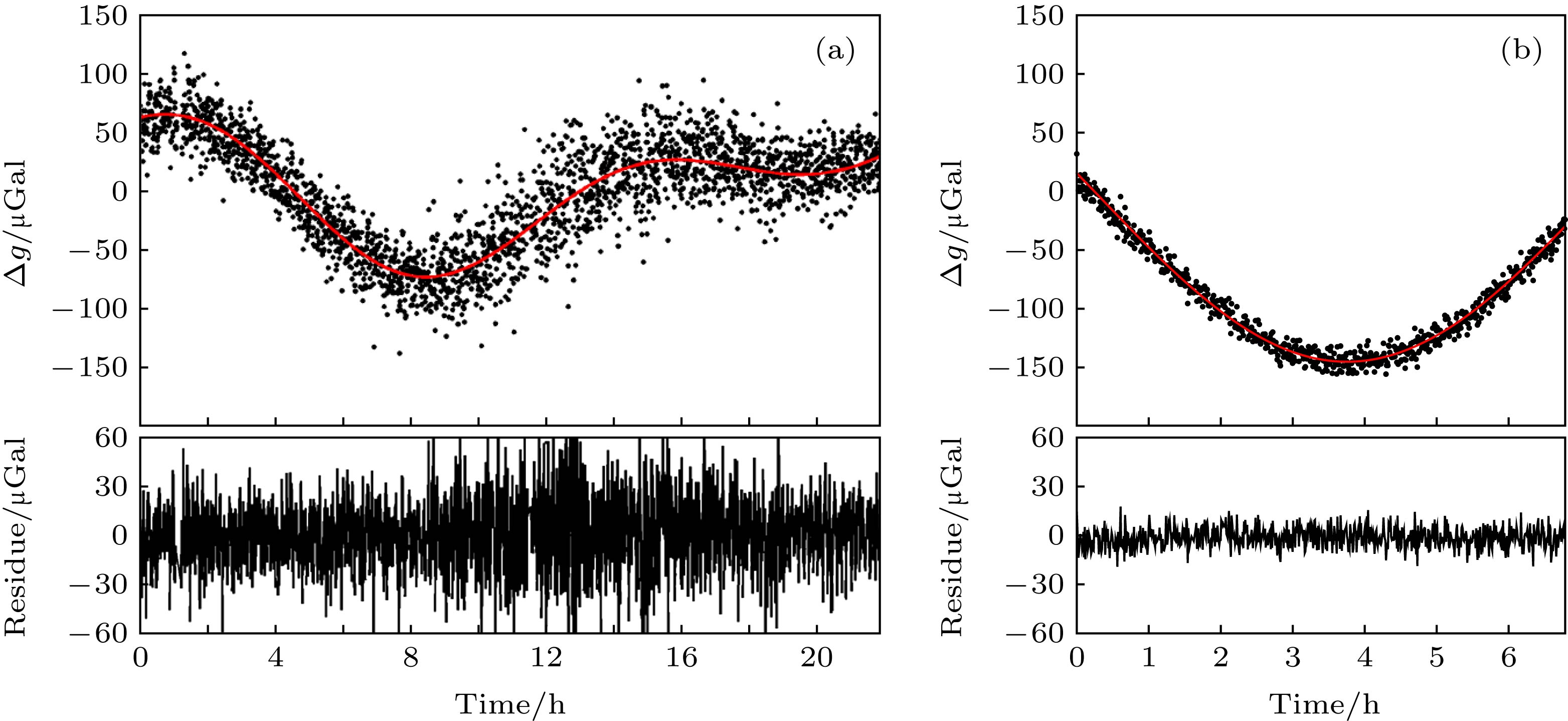
图 8 重力加速度g值的测量结果及其与理论值的残差(黑色的点为实测的数据, 红色的实线为理论潮汐模型) (a)将干涉仪探头直接放置于地面上测量得到的结果; (b)对干涉激光反射镜进行主动减振后测量得到的结果
Figure 8. Measured and theoretical data of tidal signal and the difference between them: (a) The result obtained by placing the atom interferometry probe directly on the ground; (b) the result obtained by actively vibration isolating the interferometric laser reflector. The black dot is the measured data, and the red line is the theoretical tidal model.
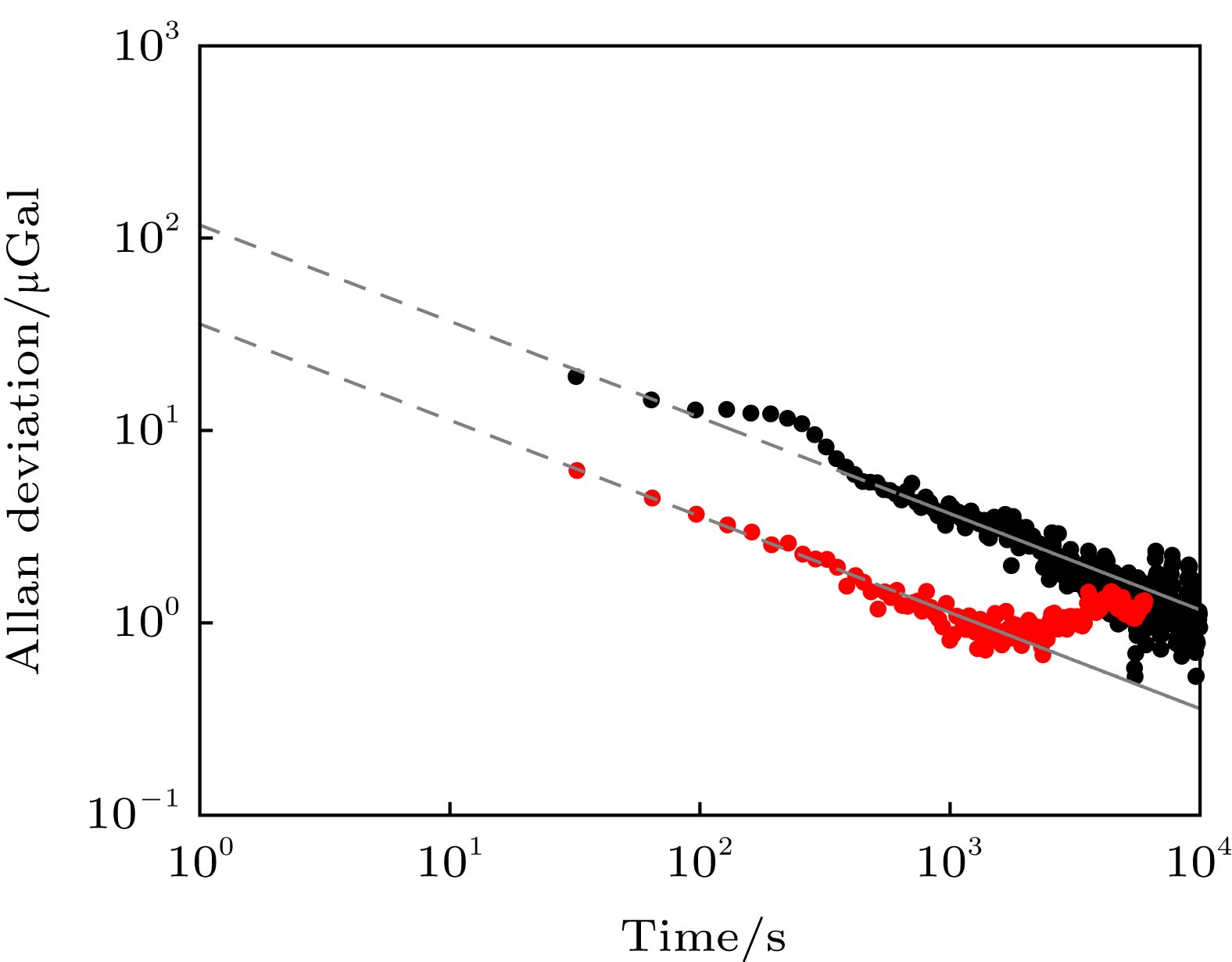
图 9 Allan方差评估结果(黑色实点为干涉仪探头直接放地面上得到的残差(Residue)的Allan方差评估结果, 评估结果显示原子重力仪直接放地面上的测量灵敏度为117 μGal/Hz1/2; 红色实点为对干涉激光反射镜进行主动减振后得到的残差(Residue)的Allan方差评估结果, 评估结果显示进行主动减振以后原子干涉仪测量灵敏度为35 μGal/Hz1/2 )
Figure 9. Allan deviations of the residual gravity accelerations. The black solid dot is the Allan deviation of the residual obtained by placing the atom interferometry probe directly on the ground. The result shows the sensitivity for the atom interferometry in this condition is 117 μGal/Hz1/2. The red solid dot is the Allan deviation of the residual obtained by actively vibration isolating the interferometric laser reflector. The result shows the sensitivity for the atom interferometry in this condition is 35 μGal/Hz1/2.
表 1 反馈控制系统参数设定值
Table 1. Parameters of the feedback control system
滤波器 截止频率
fc/Hz反馈
系数设定值 耦合
系数设定值 $H_{1}$ 0.25 $A_{1}$ 0.11 $C_{1}$ 0.01 $H_{2}$ 0.25 $A_{2}$ 9 $C_{2}$ 0.01 $H_{3}$ 0.001 $A_{3}$ 0.03 $H_{4}$ 0.45 $A_{4}$ 0.03 $H_{5}$ 0.45 $L_{1}$ 6 $L_{2}$ 6 
DownLoad: CSV
-
[1] Abbott B, Abbott R, Abbott T D, Abernathy M R, Acernese F, Ackley K, Adams C, Adams T, Addesso P, Adhikari R 2016 Phys. Rev. Lett. 116 061102
Google Scholar
[2] Abbott B P, Abbott R, Abbott T D, Acernese F, Ackley K, Adams C, Adams T, Addesso P, Adhikari R X, Adya V B 2017 Astrophys. J. 851 1
Google Scholar
[3] Matichard F, Lantz B, Mason K, Mittleman R, Abbott B, Abbott S, Allwine E, Barnum S, Birch J, Biscans S 2015 Precis. Eng. 40 273
Google Scholar
[4] Campbell S L, Hutson R, Marti G E, Goban A, Oppong N D, Mcnally R L, Sonderhouse L, Robinson J M, Zhang W, Bloom B 2017 Science 358 90
Google Scholar
[5] Ludlow A D, Boyd M M, Ye J, Peik E, Schmidt P O 2015 Rev. Mod. Phys. 87 637
Google Scholar
[6] Chen L, Hall J L, Ye J, Yang T, Zang E, Li T 2006 Phys. Rev. A 74 053801
Google Scholar
[7] Li Q, Xue C, Liu J, Wu J, Yang S, Shao C, Quan L, Tan W, Tu L, Liu Q 2018 Nature 560 582
Google Scholar
[8] Li Q, Liu J P, Xue C, Wu J F, Yang S Q, Luo J 2016 Rev. Sci. Instrum. 87 351
[9] Jones L, Wang S, Hu X, Rahman S, Castell M R 2018 Adv. Struct. Chem. Imaging 4 7
Google Scholar
[10] Wu X, Zi F, Dudley J, Bilotta R J, Canoza P, Muller H 2017 Optica 4 1545
Google Scholar
[11] Li G, Hu H, Wu K, Wang G, Wang L J 2014 Rev. Sci. Instrum. 85 104502
Google Scholar
[12] Lautier J, Volodimer L, Hardin T, Merlet S, Lours M, Santos F P D, Landragin A 2014 Appl. Phys. Lett. 105 144102
Google Scholar
[13] Hauth M, Freier C, Schkolnik V, Senger A, Schmidt M, Peters A 2013 Phys. Rev. B 113 49
[14] Nelson P G 1991 Rev. Sci. Instrum. 62 2069
Google Scholar
[15] 胡华, 伍康, 申磊, 李刚, 王力军 2012 61 099101
Google Scholar
Hu H, Wu K, Shen L, Li G, Wang L J 2012 Acta Phys. Sin. 61 099101
Google Scholar
[16] Kasevich M A, Chu S 1992 Appl. Phys. B 54 321
Google Scholar
[17] Peters A, Chung K Y, Chu S 2001 Metrologia 38 25
Google Scholar
[18] Dickerson S M, Hogan J M, Sugarbaker A, Johnson D M S, Kasevich M A 2013 Phys. Rev. Lett. 111 083001
Google Scholar
[19] Freier C, Hauth M, Schkolnik V, Keykauf B, Schilling M, Wziontek H, Scherneck H, Muller J, Peters A 2016 J. Phys.: Conf. Ser. 723 012050
Google Scholar
[20] Hu Z K, Sun B L, Duan X C, Zhou M K, Chen L L, Zhan S, Zhang Q Z, Luo J 2013 Phys. Rev. A 88 43610
Google Scholar
[21] Zhang X W, Zhong J Q, Tang B, Chen X, Zhu L, Huang P W, Wang J, Zhan M S 2018 Appl. Opt. 57 6545
Google Scholar
[22] Wang Q, Wang Z, Fu Z, Liu W, Lin Q 2016 Opt. Commun. 358 82
Google Scholar
[23] Wang S K, Zhao Y, Zhuang W, Li T C, Wu S Q, Feng J Y, Li C J 2018 Metrologia 55 360
Google Scholar
[24] Hensley J M, Peters A, Chu S 1999 Rev. Sci. Instrum. 70 2735
Google Scholar
[25] Tang B, Zhou L, Xiong Z Y, Wang J, Zhan M S 2014 Rev. Sci. Instrum. 85 093109
Google Scholar
[26] Zhou M K, Xiong X, Chen L L, Cui J F, Duan X C, Hu Z K 2015 Rev. Sci. Instrum. 86 046108
Google Scholar
[27] Cheinet P, Canuel B, Pereira D S F, Gauguet A, Yverleduc F, Landragin A 2008 IEEE Trans. Instrum. Meas. 57 1141
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 9645
- PDF Downloads: 180
- Cited By: 0
