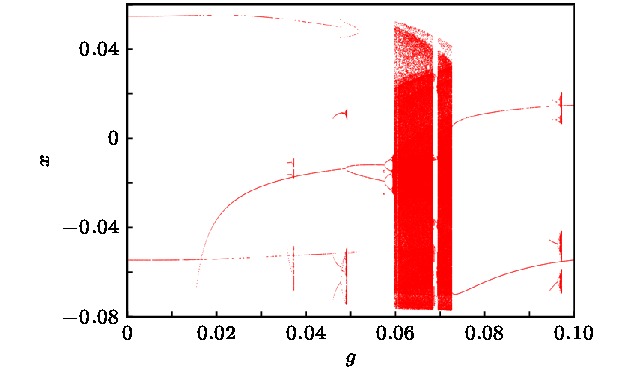
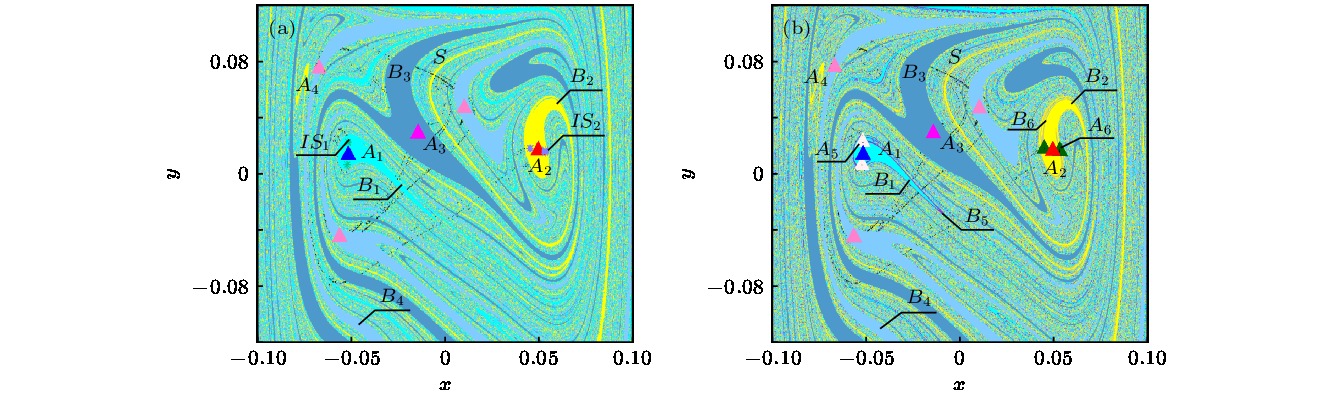
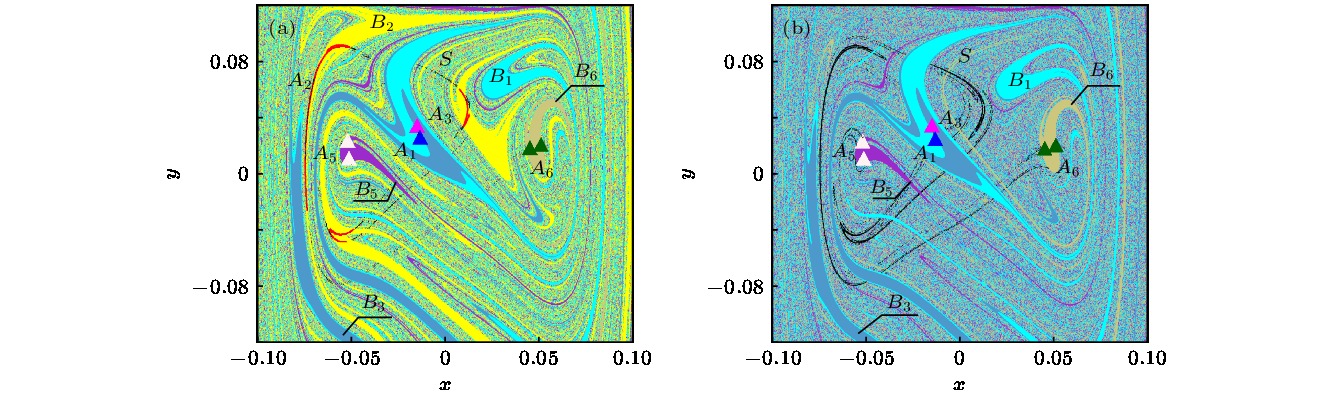
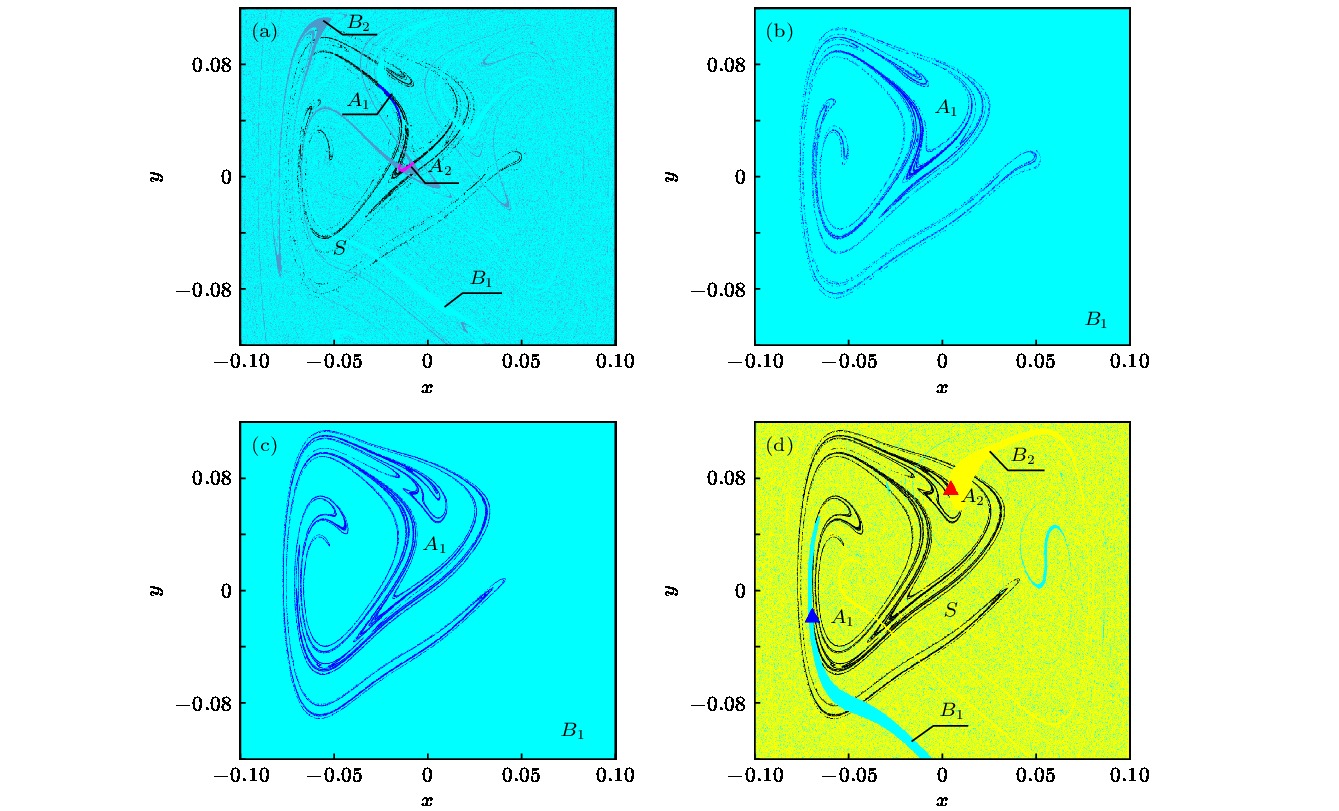
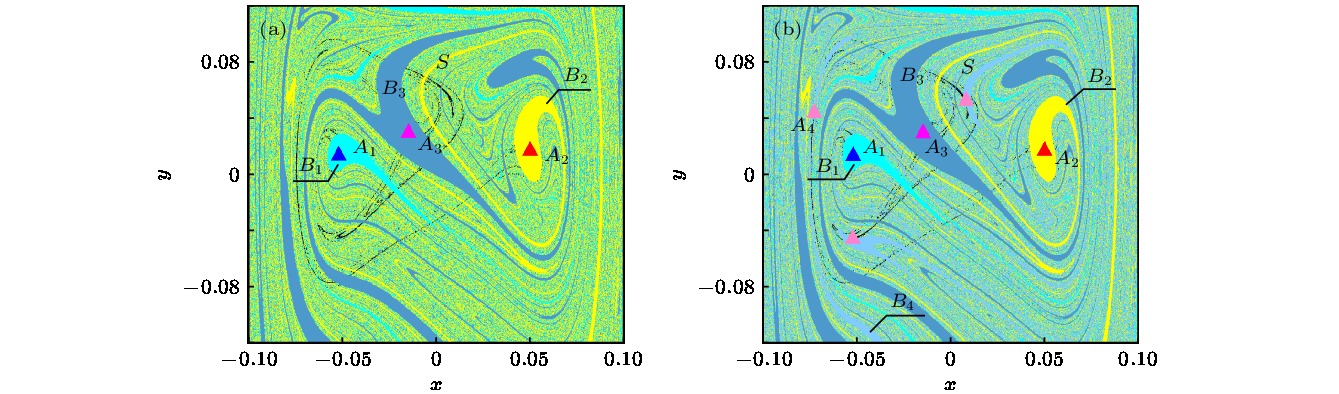
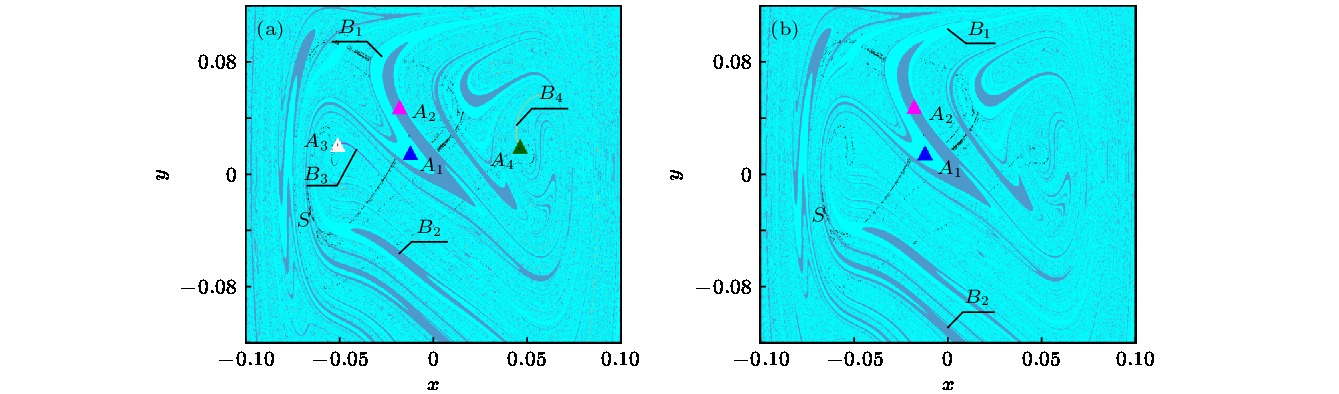
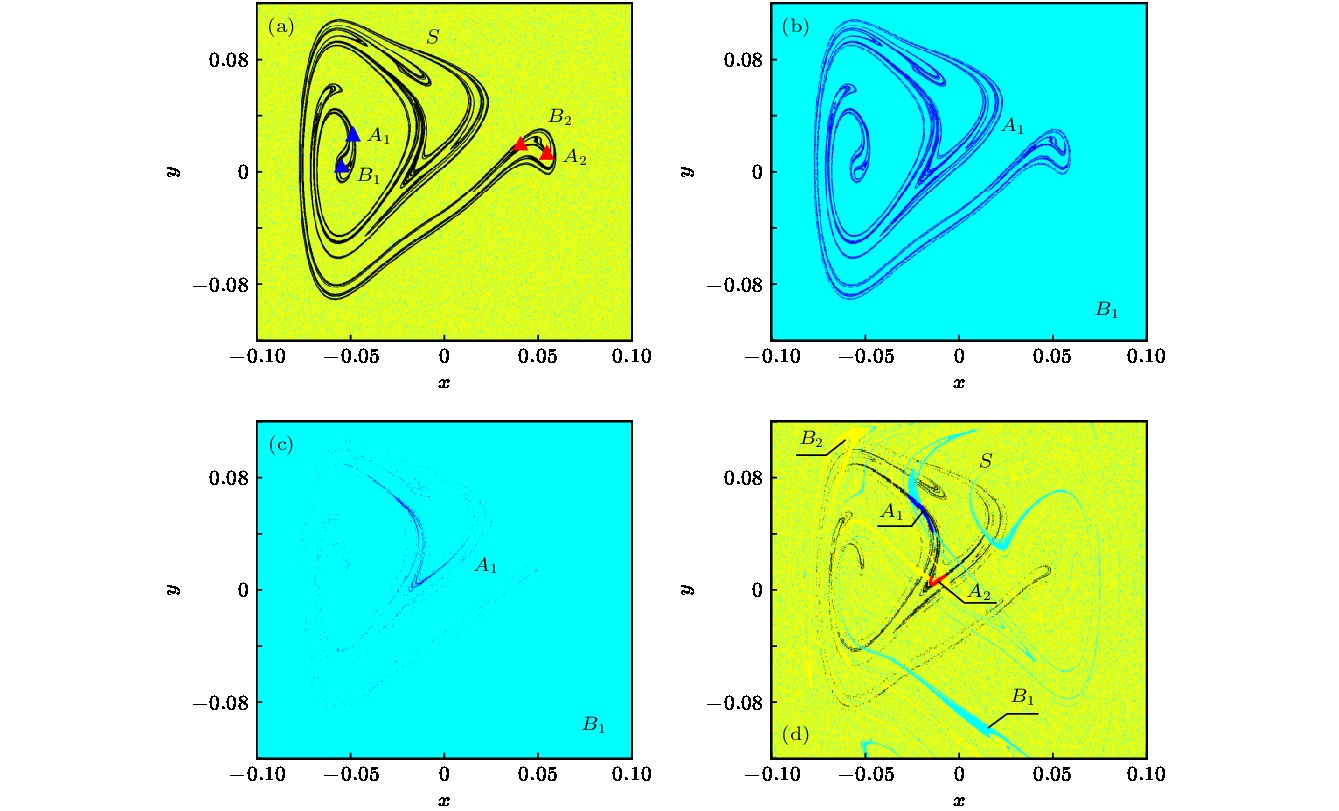
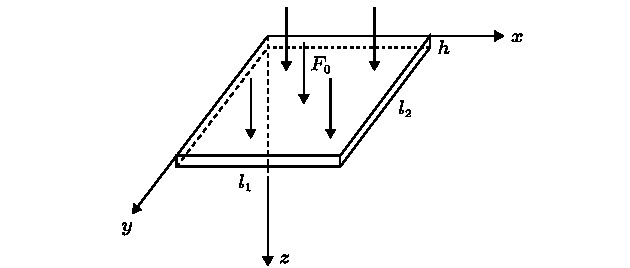
-
The unique global properties of shape memory alloy are mainly derived from the martensite phase transition and its inverse, which result from the change of temperature and external load. In this paper, the global characteristics of shape memory alloy thin plate system are analyzed with the temperature and harmonic excitation amplitude as control parameters. Based on the method of Poincare map, the complex crisis phenomenon of the system including the sudden change in number, size and type of attractors can be observed through the global multivalued bifurcation diagram. However, the specific crisis type is not clear, it is necessary to be analyzed from the global viewpoint. By computing the global diagram with the composite cell coordinate system method which constructs a composite cell state space by multistage division of the continuous phase space, the attractors, saddles and basins of attraction of the system can be obtained more accurately. The vivid evolutionary processes of the crisis phenomena of the system are illustrated, and it can be found that the system presents a complex global structure with amplitude and temperature changing. There exist two kinds of crises: one is the boundary crisis resulting from the collision between a chaotic/periodic attractor and a chaotic saddle within the basin boundary, which causes the attractor to vanish, and the other is the merging crisis caused by the collision of two or more attractors with the chaotic saddle within the basin boundary where a new chaotic attractor appears. When multiple attractors coexist in the system, the basin boundary may be smooth or fractal, and for any point at boundary, its small open neighborhood always has a nonempty intersection with three or more basins, which is known as Wada basin boundary. It is difficult to predict the dynamic behavior of the system accurately due to the fractal, the Wada-Wada, Wada-fractal and fractal-Wada basin boundary metamorphoses which can be observed along with the variation of temperature and amplitude through the composite cell coordinate system method, which owns a unique advantage in depicting basin boundary. Furthermore, the Wada property is displayed more clearly by refining specified region. The results of this paper provide a theoretical analysis tool for adjusting the dynamic response of shape memory alloy thin plate system and optimizing the deformation and vibration control of mechanical equipment through controlling temperature and excitation intensity.
-
Keywords:
- shape memory alloy /
- global dynamics /
- crisis /
- fractal basin boundary
[1] Yuan B, Zhu M, Chung C 2018 Materials 11 1716
Google Scholar
[2] Hartl D J, Lagoudas D C 2007 Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 221 535
[3] Lee J, Jin M, Ahn K K 2013 Mechatronics 23 310
Google Scholar
[4] Jani J M, Leary M, Subic A, Gibson M A 2014 Mater. Des. 56 1078
Google Scholar
[5] Song G, Ma N, Li H N 2006 Eng. Struct. 28 1266
Google Scholar
[6] Bernardini D, Rega G 2011 Int. J. Bifurcation Chaos 21 2769
Google Scholar
[7] Paula A S, Savi M A, Lagoudas D C 2012 J. Braz. Soc. Mech. Sci. Eng. 34 401
Google Scholar
[8] Sado D, Pietrzakowski M 2010 Int. J. Non-Linear Mech. 45 859
Google Scholar
[9] Hashemi S M T, Khadem S E 2006 Int. J. Mech. Sci. 48 44
Google Scholar
[10] Savi M A 2015 Int. J. Non-Linear Mech. 70 2
Google Scholar
[11] Han Q, Xu W, Yue X 2014 Int. J. Bifurcation Chaos 24 1450051
Google Scholar
[12] Grebogi C, Ott E, Yorke J A 1982 Phys. Rev. Lett. 48 1507
Google Scholar
[13] Grebogi C, Ott E, Yorke J A 1983 Physica D 7 181
Google Scholar
[14] Chian A C L, Borotto F A, Rempel E L, Rogers C 2005 Chaos Solitons Fractals 24 869
Google Scholar
[15] Yue X, Xu W, Zhang Y 2012 Nonlinear Dyn. 69 437
Google Scholar
[16] 刘莉, 徐伟, 岳晓乐, 韩群 2013 62 200501
Google Scholar
Liu L, Xu W, Yue X L, Han Q 2013 Acta Phys. Sin. 62 200501
Google Scholar
[17] 刘晓君, 洪灵, 江俊 2016 65 180502
Google Scholar
Liu X J, Hong L, Jiang J 2016 Acta Phys. Sin. 65 180502
Google Scholar
[18] Yue X, Xu W, Wang L 2013 Commun. Nonlinear Sci. Numer. Simul. 18 3567
Google Scholar
[19] Zhang Y 2013 Phys. Lett. A 377 1269
Google Scholar
[20] Hsu C S 1992 Int. J. Bifurcation Chaos 2 727
Google Scholar
[21] Hsu C S 1995 Int. J. Bifurcation Chaos 5 1085
Google Scholar
[22] Tongue B H 1987 Physica D 28 401
Google Scholar
[23] Falk F 1980 Acta Metall. Sin. 28 1773
Google Scholar
[24] Machado L G, Savi M A, Pacheco P M C L 2004 Shock Vib. 11 67
Google Scholar
[25] 黄志华, 刘平, 杜长城, 李映辉 2009 力学季刊 30 71
Google Scholar
Huang Z H, Liu P, Du C C, Li Y H 2009 Chin. Quarterly Mech. 30 71
Google Scholar
-
图 1 SMA薄板的横向振动
Figure 1. Transverse vibration of SMA thin plate.
-
[1] Yuan B, Zhu M, Chung C 2018 Materials 11 1716
Google Scholar
[2] Hartl D J, Lagoudas D C 2007 Proc. Inst. Mech. Eng. Part G: J. Aerosp. Eng. 221 535
[3] Lee J, Jin M, Ahn K K 2013 Mechatronics 23 310
Google Scholar
[4] Jani J M, Leary M, Subic A, Gibson M A 2014 Mater. Des. 56 1078
Google Scholar
[5] Song G, Ma N, Li H N 2006 Eng. Struct. 28 1266
Google Scholar
[6] Bernardini D, Rega G 2011 Int. J. Bifurcation Chaos 21 2769
Google Scholar
[7] Paula A S, Savi M A, Lagoudas D C 2012 J. Braz. Soc. Mech. Sci. Eng. 34 401
Google Scholar
[8] Sado D, Pietrzakowski M 2010 Int. J. Non-Linear Mech. 45 859
Google Scholar
[9] Hashemi S M T, Khadem S E 2006 Int. J. Mech. Sci. 48 44
Google Scholar
[10] Savi M A 2015 Int. J. Non-Linear Mech. 70 2
Google Scholar
[11] Han Q, Xu W, Yue X 2014 Int. J. Bifurcation Chaos 24 1450051
Google Scholar
[12] Grebogi C, Ott E, Yorke J A 1982 Phys. Rev. Lett. 48 1507
Google Scholar
[13] Grebogi C, Ott E, Yorke J A 1983 Physica D 7 181
Google Scholar
[14] Chian A C L, Borotto F A, Rempel E L, Rogers C 2005 Chaos Solitons Fractals 24 869
Google Scholar
[15] Yue X, Xu W, Zhang Y 2012 Nonlinear Dyn. 69 437
Google Scholar
[16] 刘莉, 徐伟, 岳晓乐, 韩群 2013 62 200501
Google Scholar
Liu L, Xu W, Yue X L, Han Q 2013 Acta Phys. Sin. 62 200501
Google Scholar
[17] 刘晓君, 洪灵, 江俊 2016 65 180502
Google Scholar
Liu X J, Hong L, Jiang J 2016 Acta Phys. Sin. 65 180502
Google Scholar
[18] Yue X, Xu W, Wang L 2013 Commun. Nonlinear Sci. Numer. Simul. 18 3567
Google Scholar
[19] Zhang Y 2013 Phys. Lett. A 377 1269
Google Scholar
[20] Hsu C S 1992 Int. J. Bifurcation Chaos 2 727
Google Scholar
[21] Hsu C S 1995 Int. J. Bifurcation Chaos 5 1085
Google Scholar
[22] Tongue B H 1987 Physica D 28 401
Google Scholar
[23] Falk F 1980 Acta Metall. Sin. 28 1773
Google Scholar
[24] Machado L G, Savi M A, Pacheco P M C L 2004 Shock Vib. 11 67
Google Scholar
[25] 黄志华, 刘平, 杜长城, 李映辉 2009 力学季刊 30 71
Google Scholar
Huang Z H, Liu P, Du C C, Li Y H 2009 Chin. Quarterly Mech. 30 71
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7045
- PDF Downloads: 67
- Cited By: 0
