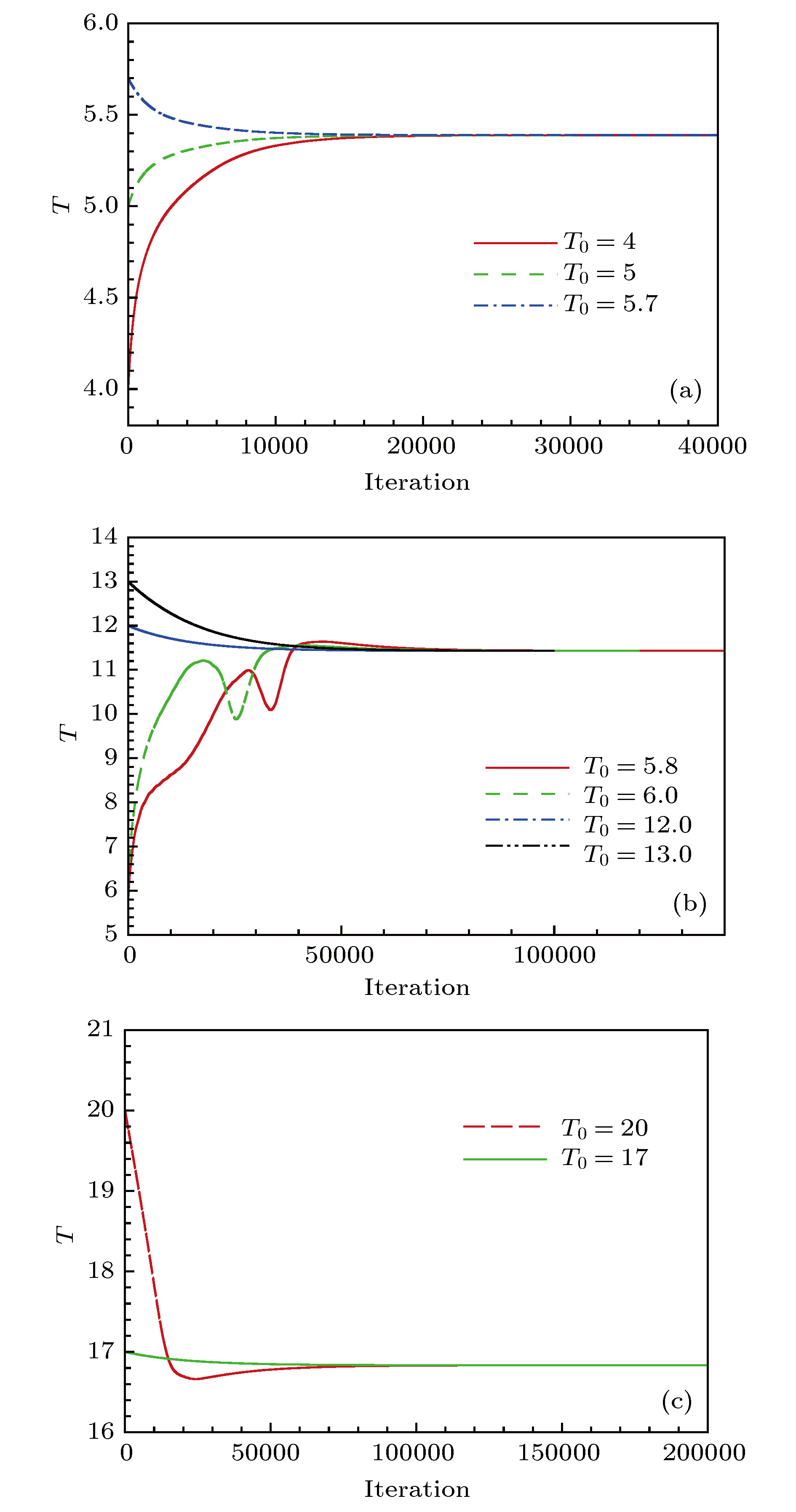
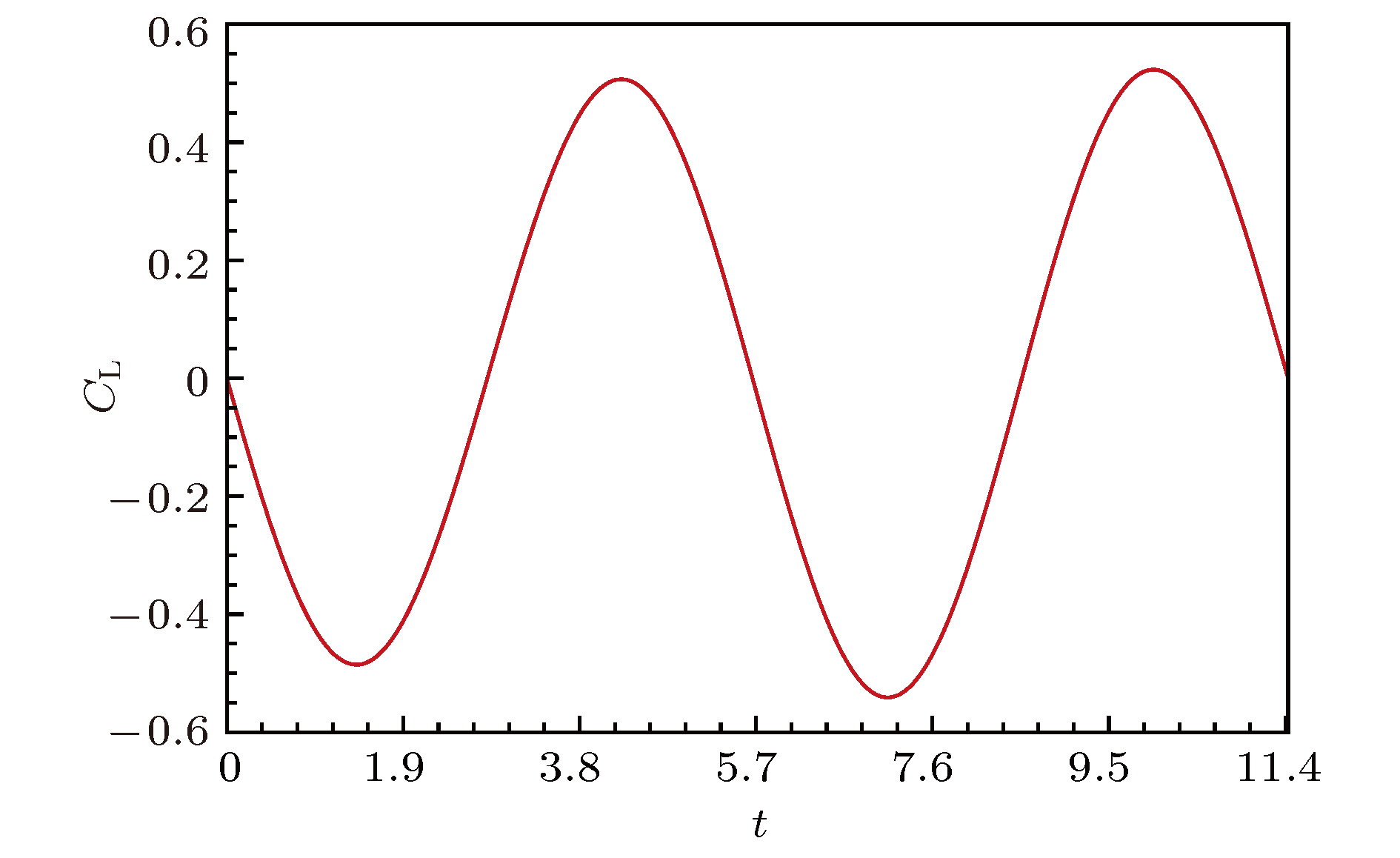
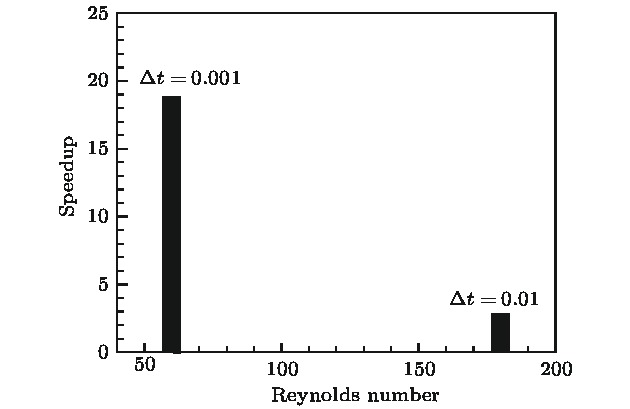
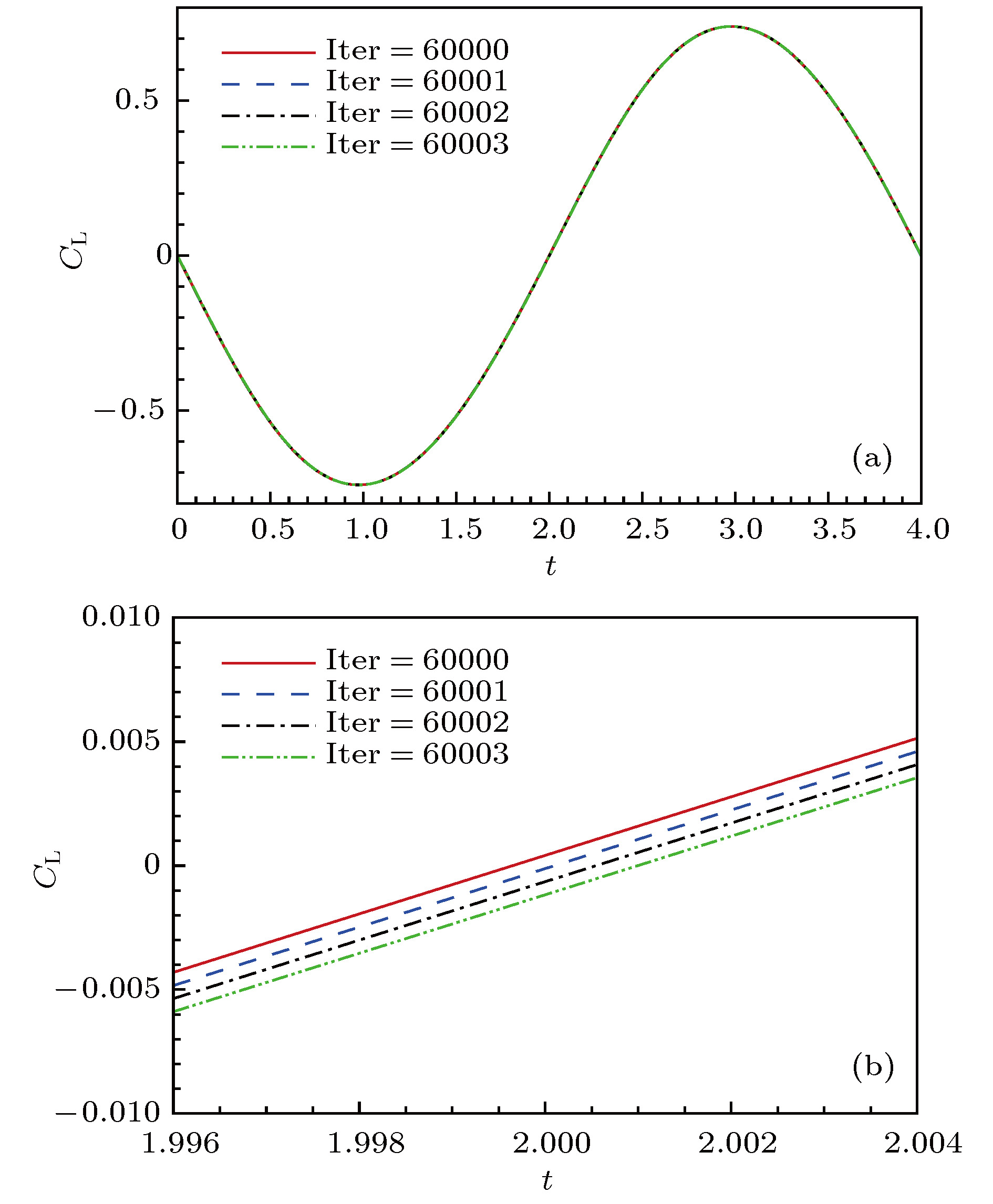
-
The harmonic balance method (HBM) is an efficient frequency-domain approach to computing periodically unsteady flows. The basic principle of this method is to decompose the flow variables into a Fourier series, and transform the unsteady flow into several steady problems coupled by a spectral time-derivative operator, from which the whole time history of a complete unsteady periodic flow can be reconstructed. In the present work, we investigate the ability of the HBM to be used for modeling the periodic unsteady vortex shedding behind a bluff body at low Reynolds numbers via solving the unsteady incompressible Navier-Stokes equations. For the periodic problem where the time period T of the unsteadiness is unknown, a variable-time-period method based on residual gradients is used to compute the exact time period iteratively starting from an initial guess T0. By simulating the two-dimensional laminar flows over a circular cylinder and a square cylinder, the accuracy and efficiency of the HBM are investigated and the effects of different parameters on the final results are analyzed. Comparisons with the results of fixed-time-period HBM using a constant time period are also implemented. Three practical methods of optimization are used to iterate the time period, and the values of accuracy and efficiency of different methods are compared with each other. The results show that the HBM can accurately capture the complex nonlinear flow field physics with only three harmonics. The Strouhal frequency and mean drag coefficient each as a function of the Reynolds number agree well with existing experimental and computational data. For both test cases, the computational efficiency of HBM is higher than that from the traditional time-domain method. For the square cylinder test case, the HBM offers speedup rate up to nearly 18 times. The real time period of vortex shedding can be predicted by the gradient based variable-time-period method, and the final result is insensitive to search step λ. The calculation result is sensitive to the initial T0, and when such a variable is greater than a certain value, the result will converge to an approximate integer multiple of the real one. Therefore, it deserves further exploration on how to specify this initial condition. The shedding time periods computed by different optimization methods are converged to the same value. The computational efficiency from the FR conjugate gradient method and that from Newton method are both equivalent to that from the steepest descent method with the maximum search step λ = 100. Avoiding prescribing parameters such as the search step λ, the Newton method possesses higher application value in engineering calculation than the other two schemes.
-
Keywords:
- periodic unsteady flows /
- numerical simulation /
- harmonic balance method /
- variable-time-period method
[1] McMullen M, Jameson A, Alonso J 2006 AIAA J. 44 1428
Google Scholar
[2] Mosahebi A, Nadarajah S 2013 Comput. Fluids 75 140
Google Scholar
[3] Hall K C, Grawley E F 1989 AIAA J. 27 777
Google Scholar
[4] Zhang Z, Yang S, Chen P C 2012 J. Aircraft 49 922
Google Scholar
[5] Ning W, He L 1998 J. Turbomach. 120 508
Google Scholar
[6] Hall K C, Thomas J P, Clark W S 2002 AIAA J. 40 879
Google Scholar
[7] Ekici K, Hall K C 2007 AIAA J. 45 1047
Google Scholar
[8] McMullen M, Jameson A, Alonso J 2001 39th Aerospace Sciences Meeting and Exhibit Reno, NV, January 8−11, 2001 AIAA 2001-0152
[9] Gopinath A, Jameson A 2005 43rd AIAA Aerospace Sciences Meeting and Exhibit Reno, Nevada, January 10−13, 2005 AIAA 2005-1220
[10] Rubino A, Pini M, Colonna P, Albring T, Nimmagadda S, Economon T, Alonso J 2018 J. Comput. Phys. 372 220
Google Scholar
[11] Lindblad D, Montero Villar G, Andersson N, Capitao Patrao A, Courty-Audren S K, Napias G 2018 AIAA Aerospace Sciences Meeting Kissimmee, Florida, January 8−12, 2018 AIAA 2018-1004
[12] Reddy T S R, Bakhle M 2009 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit Denver, Colorado, August 2−5, 2009 AIAA 2009-5420
[13] Cvijetic G, Jasak H 2018 AIAA Aerospace Sciences Meeting Kissimmee, Florida, January 8−12, 2018 AIAA 2018-0833
[14] Hall K C, Thomas J P, Ekici K, Voytovych D M 2003 33rd AIAA Fluid Dynamics Conference and Exhibit Orlando, Florida, June 23−26, 2003 AIAA 2003-3998
[15] Hall K C, Ekici K, Thomas J P, Dowell E H 2013 Int. J. Comput. Fluid Dyn. 27 54
[16] Lindblad D, Andersson N 2017 55th AIAA Aerospace Sciences Meeting Grapevine, Texas, January 9−13, 2017 AIAA 2017-1171
[17] 杜鹏程, 宁方飞 2017 航空动力学报 32 528
Du P C, Ning F F 2017 Journal of Aerospace Power 32 528
[18] Thomas J P, Custer C H, Dowell E H, Hall K C, Corre C 2013 AIAA J. 51 1374
Google Scholar
[19] Thomas J P, Custer C H, Dowell E H, Hall K C 19th AIAA Computational Fluid Dynamics San Antonio, Texas, June 22−25, 2009 AIAA 2009-4270
[20] Guillaume D, Frédéric S, Guillaume P 2010 AIAA J. 48 788
Google Scholar
[21] Ekici K, Hall K C, Dowell E H 2008 J. Comput. Phys. 227 6206
Google Scholar
[22] Da Ronch A, Vallespin D, Ghoreyshi M, Badcock K J 2012 AIAA J. 50 470
Google Scholar
[23] Da Ronch A, McCracken A J, Badcock K J, Widhalm M, Campobasso M S 2013 J. Aircraft 50 694
Google Scholar
[24] Murman S M 2005 43rd AIAA Aerospace Sciences Meeting Reno, NV, January 10−13, 2005 AIAA 2005-0840
[25] Hassan D, Sicot F 2011 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition Orlando, Florida, January 4−7, 2011 AIAA 2011-1242
[26] 陈琦, 陈坚强, 袁先旭, 谢昱飞 2014 力学学报 46 183
Google Scholar
Chen Q, Chen J Q, Yuan X X, Xie Y F 2014 Chinese Journal of Theoretical and Applied Mechanics 46 183
Google Scholar
[27] 柴振霞, 刘伟, 刘绪, 杨小亮 2018 国防科技大学学报 40 30
Google Scholar
Chai Z X, Liu W, Liu X, Yang X L 2018 J. Nat. Univ. Defense Technol. 40 30
Google Scholar
[28] Clark E B, Ekici K, Beran P S 2014 44th AIAA Fluid Dynamics Conference Atlanta, GA, June 16−20, 2014 AIAA 2014-3323
[29] Cvijetic G, Jasak H, Vukcevic V 2016 54th AIAA Aerospace Sciences Meetin San Diego, California, USA, January 4−8, 2016 AIAA 2006-0070
[30] McMullen M, Jameson A, Alonso J J 2002 40th AIAA Aerospace Sciences Meeting & Exhibit Reno, NV, January 14−17, 2002 AIAA 2002-0120
[31] Gopinath A K, Jameson A 2006 44th AIAA Aerospace Sciences Meeting and Exhibit Reno, Nevada, January 9−12, 2006 AIAA 2006-449
[32] Spiker M A, Thomas J P, Hall K C, Kielb R E, Dowell E H 2006 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference Newport, Rhode Island, May 1−4, 2006 AIAA 2006-1965
[33] Mosahebi A, Nadarajah S K 2010 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition Orlando, Florida, January 4−7, 2010 AIAA 2010-1267
[34] Yao W, Jaiman R K 2016 J. Fluids Struct. 65 313
Google Scholar
[35] Yao W, Marques S 2015 AIAA J. 53 2040
Google Scholar
[36] 张炜, 席光 2009 西安交通大学学报 43 114
Google Scholar
Zhang W, Xi G 2009 Journal of Xi'an Jiaotong University 43 114
Google Scholar
[37] Jameson A 1991 10th Computational Fluid Dynamics Conference Honolulu, HI, June 24−26, 1991 AlAA 1991-1596
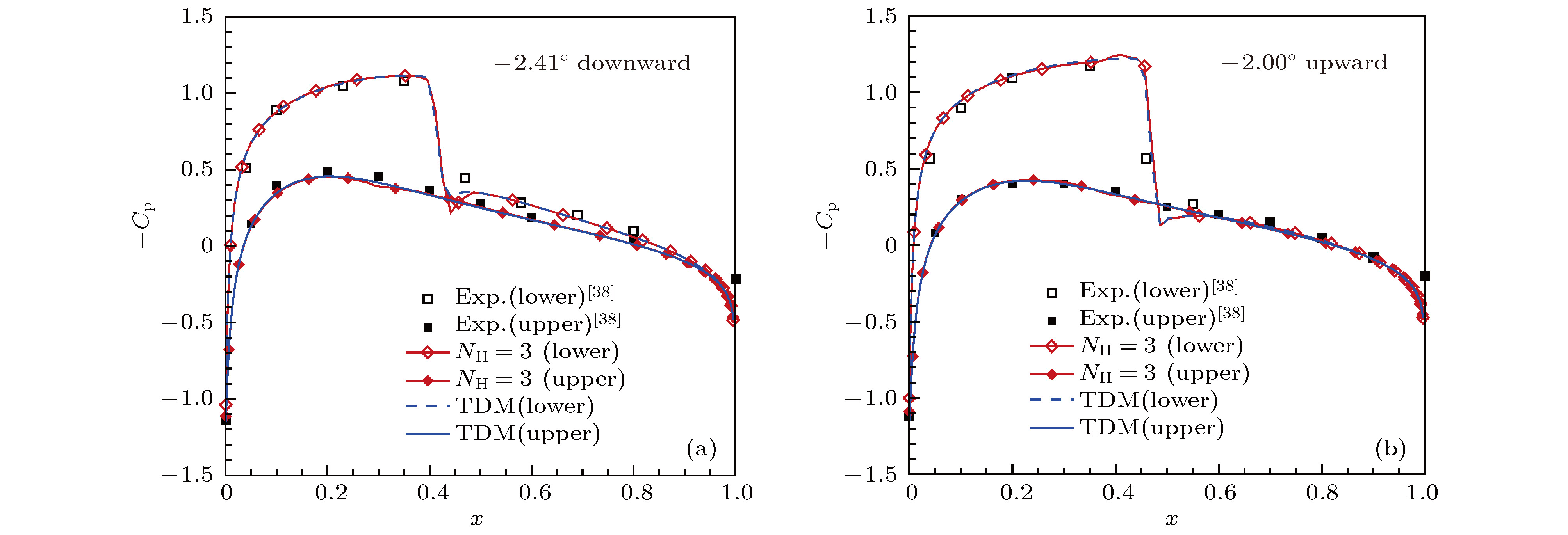
[38] Landon R H 1982 NACA 0012 Oscillatory and Transient Pitching Tech. Rep. AGARD-R-702
[39] Batina J T 1990 AIAA J. 28 1381
Google Scholar
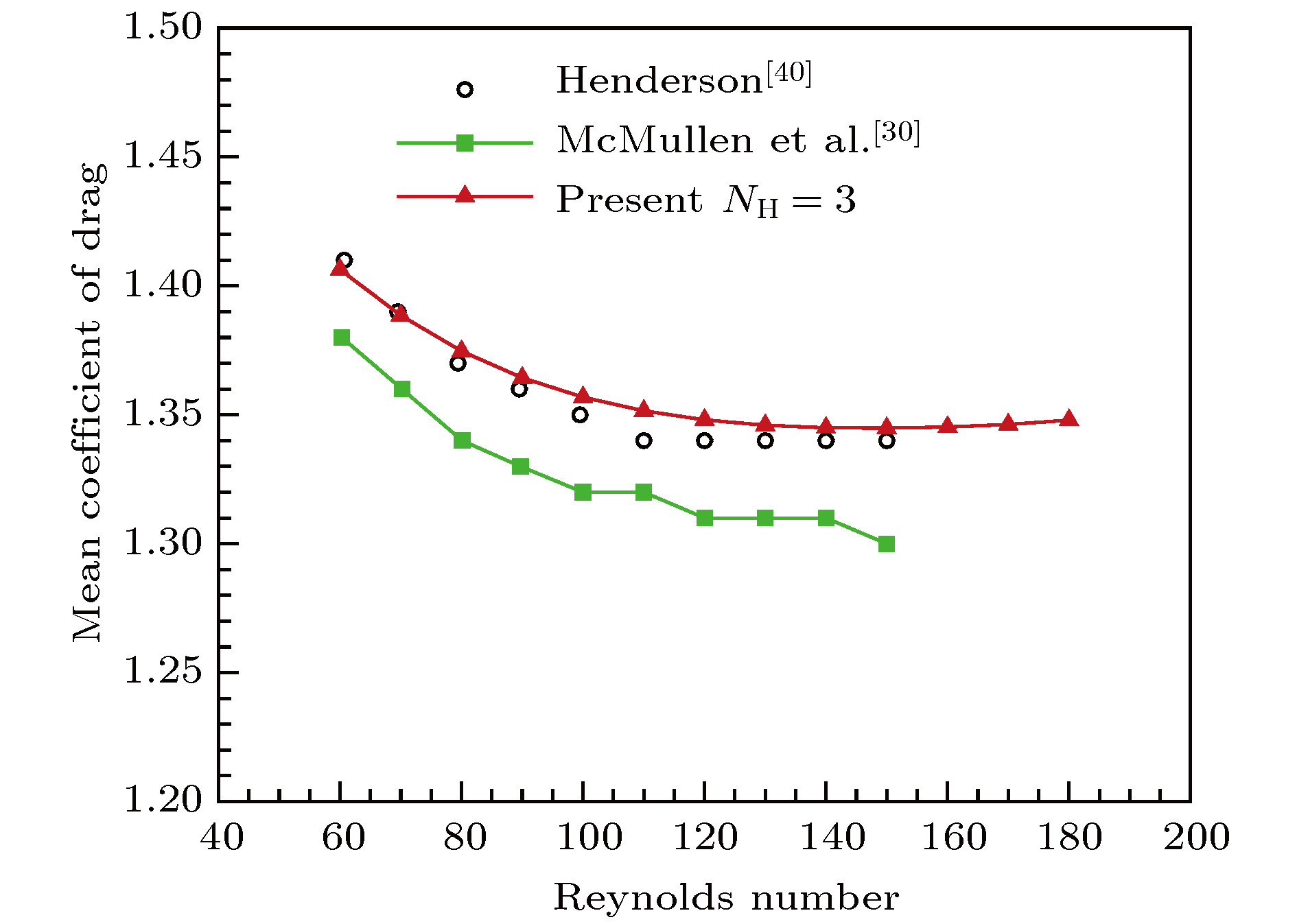
[40] Henderson R D 1995 Phys. Fluids 7 2102
Google Scholar
[41] Wieselsberger C 1922 Physik. Z. 22 321
[42] Roshko A 1954 On the Development of Turbulent Wakes From Vortex Streets (California Institute of Technology, NACA) Tech. Rep. 1191
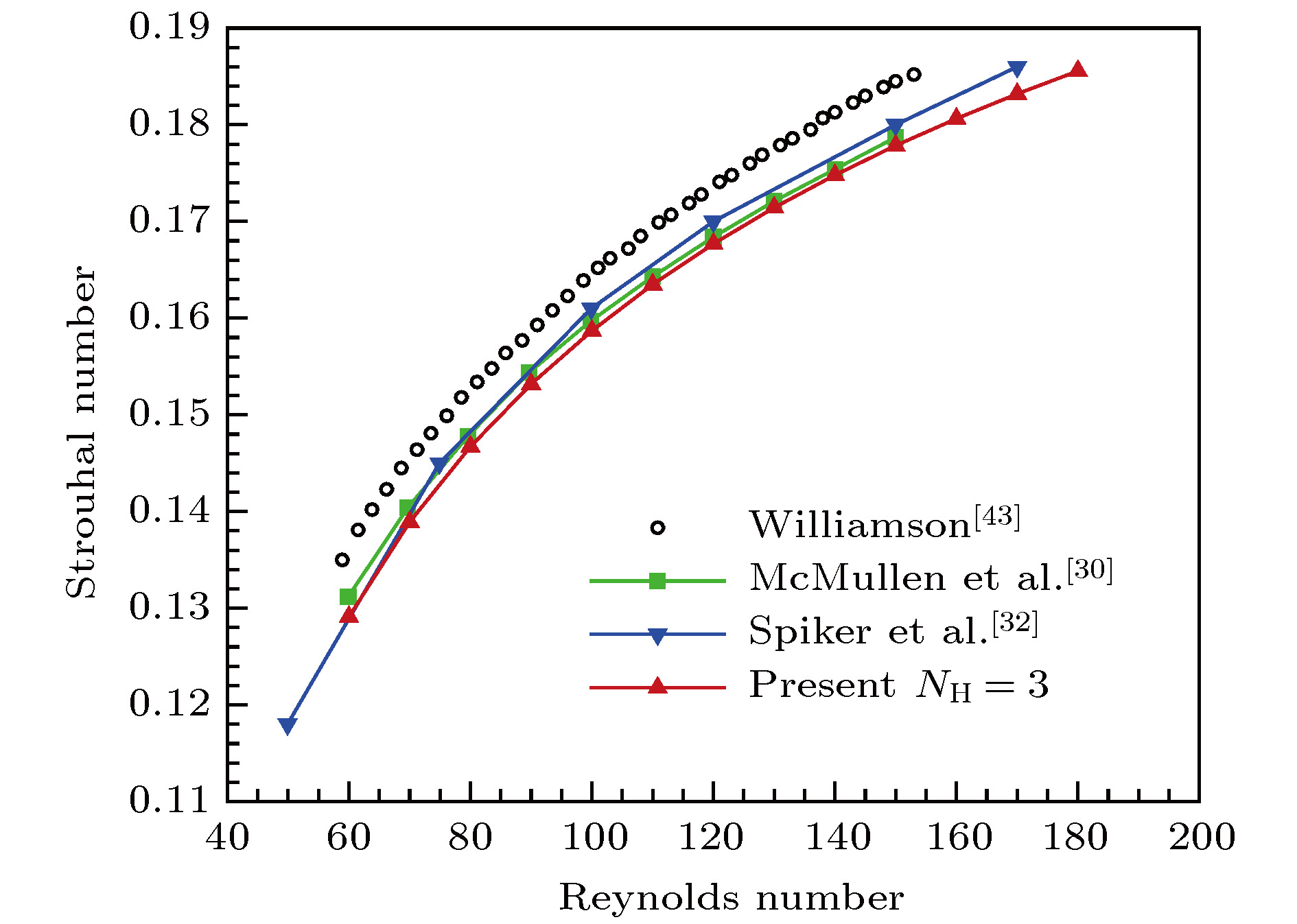
[43] Williamson C H K 1988 Phys. Fluids 31 2742
Google Scholar
[44] Williamson C H K 1998 J. Fluids Struct. 12 1073
Google Scholar
[45] 张宝林 2005 最优化理论与算法 (北京: 清华大学出版社)
Zhang B L 2005 Theory and Algorithms of Optimization (Beijing: Tsinghua University Press) (in Chinese)
[46] Sohankar A, Davidson L, Norberg C 1995 Twelfth Australaian Fluid Mechanics Conference Sydney, Australia, December, 199 p517
-
图 1 NACA0012翼型计算网格
Figure 1. Mesh for the NACA0012 airfoil.
图 2 NACA0012翼型的(a)升力系数和(b)俯仰力矩系数迟滞曲线
Figure 2. (a) Lift and (b) pitching moment coefficients dynamic dependence of NACA0012 airfoil.
图 3 NACA0012翼型俯仰振荡过程中的瞬时压力系数分布 (a) 攻角减小过程中α = –2.41°; (b) 攻角增大过程中α = –2.00°
Figure 3. Instantaneous pressure coefficient distribution compared to experimental data of NACA0012 airfoil: (a) α = –2.41° for decreasing angle; (b) α = –2.00° for increasing angle.
图 4 HBM取不同谐波数时俯仰力矩系数收敛曲线 (a) NH = 1; (b) NH = 3
Figure 4. Pitching moment coefficient convergence history for the HBM with respect to the number of harmonics: (a) NH = 1; (b) NH = 3.
图 5 CPU时间加速比随谐波数的变化
Figure 5. CPU time speedup of the HBM with respect to the TDM.
图 6 二维圆柱计算网格
Figure 6. Computational grid for cylinder in cross flow.
图 7 升、阻力系数收敛曲线
Figure 7. Time history of lift coefficient CL and drag CD.
图 8 不同谐波数下的周期T收敛曲线
Figure 8. Convergence from initial guess to exact time period with varying number of harmonics.
图 9 升力系数收敛曲线(NH = 3)
Figure 9. Time history of lift coefficient CL with NH = 3.
图 10 升力系数随时间的变化
Figure 10. Variation of CL over one period.
图 11 阻力系数随时间的变化
Figure 11. Variation of CD over one period.
图 12 Re = 180, NH = 3条件下不同时刻的流线图 (a) t = T/3; (b) t = 2T/3; (c) t = T
Figure 12. Streamlines at various time instances over one period (Re = 180, NH = 3): (a) t = T/3; (b) t = 2T/3; (c) t = T.
图 13 熵等值线图(CL最小时刻) (a) TDM计算结果; (b) HBM计算结果（NH = 3）
Figure 13. Comparison of instantaneous entropy contours: (a) TDM results; (b) HBM results (NH = 3).
图 14 Strouhal数随Re的变化
Figure 14. Strouhal number as a function of Reynolds number.
图 15 平均阻力系数随Re的变化
Figure 15. Mean coefficient of drag versus Reynolds number.
图 16 不同步长λ下的周期T收敛曲线
Figure 16. Time period convergence computed with three different step sizes λ.
图 17 不同步长T0下计算的周期T收敛曲线
Figure 17. Time period convergence with various starting guesses T0.
图 18 T = 11.43 时重建的升力系数曲线
Figure 18. Variation of CL over one period with converged time period T = 11.43.
图 19 HBM计算的St与TDM计算结果的对比
Figure 19. Comparison of the HBM St data results with TDM results.
图 20 不同雷诺下的加速比
Figure 20. CPU time speedup of various Reynolds number.
图 21 升力系数和t = T时刻的残差收敛曲线(Re = 180, T = 4, NH = 3) (a)升力系数; (b)残差
Figure 21. Time history of lift coefficient CL at various time instances over one period and residual at t = T (Re = 180, T = 4, NH = 3): (a) Lift coefficient; (b) residual.
图 22 不同迭代步重建的升力系数随时间的变化(Re = 180, T = 4, NH = 3) (a)整体; (b)局部
Figure 22. Variation of CL over one period at different iterations: (a) Overall; (b) local.
图 23 T = 5.389时各个时刻升力系数收敛曲线(NH = 3)
Figure 23. Time history of lift coefficient CL at various time instances over one period with T = 5.389 (NH = 3).
图 24 相位差随周期T的变化(Re = 180, NH = 3)
Figure 24. Change in phase of unsteady lift versus time period for Re = 180 (NH = 3).
图 25 残差随周期T的变化(Re = 180, NH = 3)
Figure 25. HBM solution residual versus time period for Re = 180 (NH = 3).
图 26 采用牛顿法和SDM计算的周期T收敛曲线对比图 (a)初始T0 = 4; (b)初始T0 = 5.41
Figure 26. Convergence of shedding time period computed by Newton method and SDM: (a) T0 = 4; (b) T0 = 5.41.
图 27 采用FR法计算的周期T收敛曲线(a)及其与SDM计算结果的比较(b)
Figure 27. Convergence of shedding time period computed by FR conjugate gradient method (a) and compared with the SDM results (b).
图 28 采用三种不同优化方法计算得到的周期T收敛曲线图
Figure 28. Convergence of shedding time period computed by three different methods of optimization.
图 29 二维方柱绕流计算网格
Figure 29. Computational grid for rectangular in cross flow.
图 30 升力系数随时间的变化
Figure 30. Comparison of lift coefficients of HBM and TDM at Re = 100.
图 31 熵等值线图(CL最小时刻) (a) TDM计算结果; (b) HBM计算结果(NH = 3)
Figure 31. Comparison of the instantaneous entropy contours: (a) TDM results; (b) HBM results (NH = 3).
表 1 NACA0012翼型俯仰振荡AGARD CT5算例计算条件
Table 1. Computational conditions of the AGARD CT5 test case for the NACA0012 airfoil.
Parameter Value Ma 0.755 α0 0.016° αm 2.51° k 0.1628 
DownLoad: CSV
表 2 时域计算结果与实验结果对比
Table 2. Time-averaged coefficient and Strouhal number compared with experiment data.
DownLoad: CSV
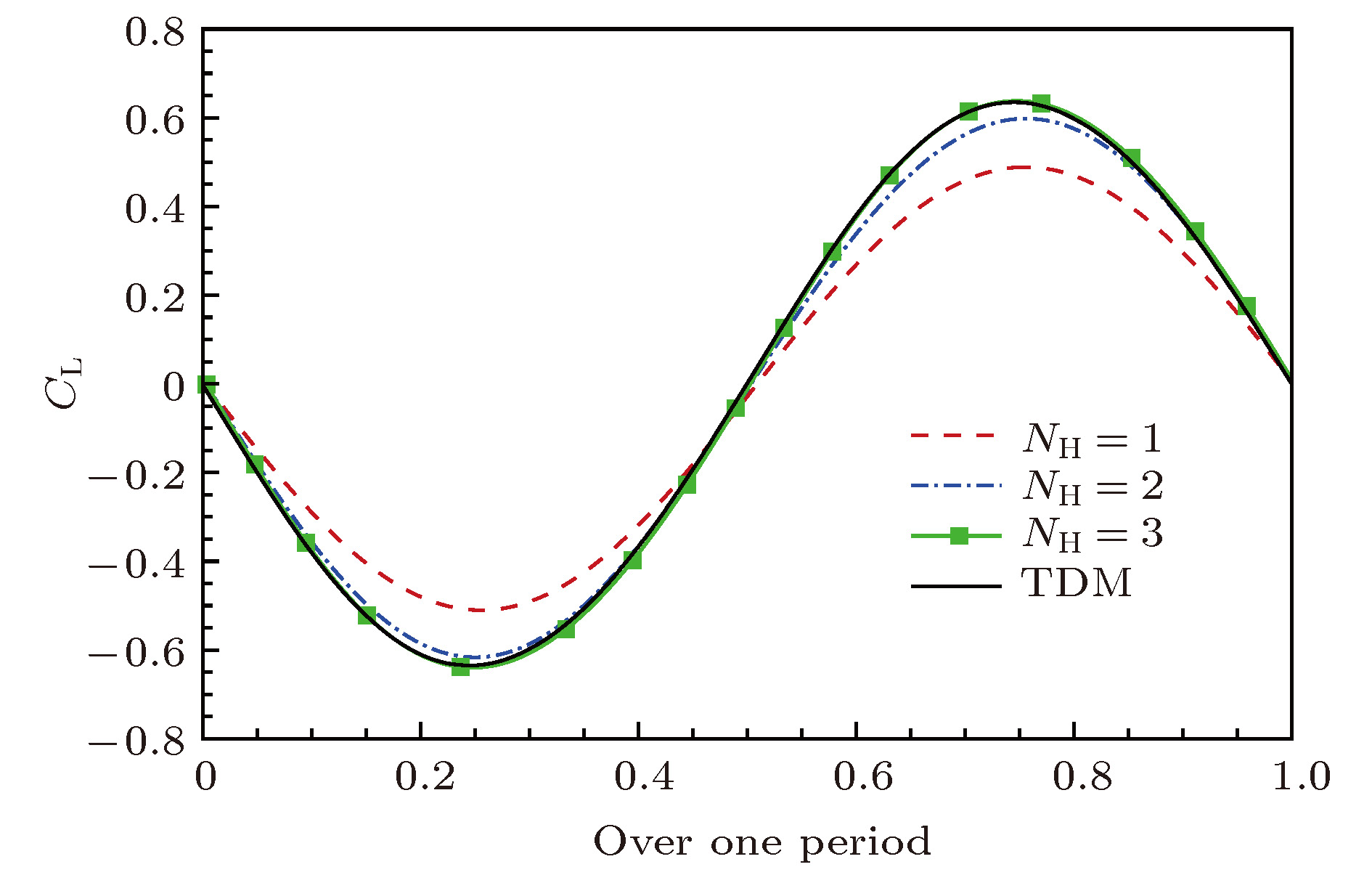
表 3 不同谐波数下的计算结果
Table 3. Strouhal number and time-averaged coefficient computed by different number of harmonics.
NH St CD0 1 0.1745 1.2817 2 0.188 1.3440 3 0.1856 1.3479 4 0.1857 1.3506 TDM 0.185 1.3457 Roshko[42] 0.185
DownLoad: CSV
表 4 时域计算结果
Table 4. Time-averaged coefficient and Strouhal number computed by time-domain solver using different physical time steps.
∆t St Cd, avg 0.1 0.134 1.443 0.01 0.1415 1.487 Sohankar[46] 0.142 1.466
DownLoad: CSV
表 5 Re = 100时不同谐波数下的计算结果对比
Table 5. Convergency of frequency and time-averaged coefficient with speedup estimates.
NH St Cd, avg Speedup 2 0.1419 1.4846 23.27 3 0.1414 1.4863 17.88 4 0.1414 1.4865 1.944 TDM 0.1415 1.487 1
DownLoad: CSV
-
[1] McMullen M, Jameson A, Alonso J 2006 AIAA J. 44 1428
Google Scholar
[2] Mosahebi A, Nadarajah S 2013 Comput. Fluids 75 140
Google Scholar
[3] Hall K C, Grawley E F 1989 AIAA J. 27 777
Google Scholar
[4] Zhang Z, Yang S, Chen P C 2012 J. Aircraft 49 922
Google Scholar
[5] Ning W, He L 1998 J. Turbomach. 120 508
Google Scholar
[6] Hall K C, Thomas J P, Clark W S 2002 AIAA J. 40 879
Google Scholar
[7] Ekici K, Hall K C 2007 AIAA J. 45 1047
Google Scholar
[8] McMullen M, Jameson A, Alonso J 2001 39th Aerospace Sciences Meeting and Exhibit Reno, NV, January 8−11, 2001 AIAA 2001-0152
[9] Gopinath A, Jameson A 2005 43rd AIAA Aerospace Sciences Meeting and Exhibit Reno, Nevada, January 10−13, 2005 AIAA 2005-1220
[10] Rubino A, Pini M, Colonna P, Albring T, Nimmagadda S, Economon T, Alonso J 2018 J. Comput. Phys. 372 220
Google Scholar
[11] Lindblad D, Montero Villar G, Andersson N, Capitao Patrao A, Courty-Audren S K, Napias G 2018 AIAA Aerospace Sciences Meeting Kissimmee, Florida, January 8−12, 2018 AIAA 2018-1004
[12] Reddy T S R, Bakhle M 2009 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit Denver, Colorado, August 2−5, 2009 AIAA 2009-5420
[13] Cvijetic G, Jasak H 2018 AIAA Aerospace Sciences Meeting Kissimmee, Florida, January 8−12, 2018 AIAA 2018-0833
[14] Hall K C, Thomas J P, Ekici K, Voytovych D M 2003 33rd AIAA Fluid Dynamics Conference and Exhibit Orlando, Florida, June 23−26, 2003 AIAA 2003-3998
[15] Hall K C, Ekici K, Thomas J P, Dowell E H 2013 Int. J. Comput. Fluid Dyn. 27 54
[16] Lindblad D, Andersson N 2017 55th AIAA Aerospace Sciences Meeting Grapevine, Texas, January 9−13, 2017 AIAA 2017-1171
[17] 杜鹏程, 宁方飞 2017 航空动力学报 32 528
Du P C, Ning F F 2017 Journal of Aerospace Power 32 528
[18] Thomas J P, Custer C H, Dowell E H, Hall K C, Corre C 2013 AIAA J. 51 1374
Google Scholar
[19] Thomas J P, Custer C H, Dowell E H, Hall K C 19th AIAA Computational Fluid Dynamics San Antonio, Texas, June 22−25, 2009 AIAA 2009-4270
[20] Guillaume D, Frédéric S, Guillaume P 2010 AIAA J. 48 788
Google Scholar
[21] Ekici K, Hall K C, Dowell E H 2008 J. Comput. Phys. 227 6206
Google Scholar
[22] Da Ronch A, Vallespin D, Ghoreyshi M, Badcock K J 2012 AIAA J. 50 470
Google Scholar
[23] Da Ronch A, McCracken A J, Badcock K J, Widhalm M, Campobasso M S 2013 J. Aircraft 50 694
Google Scholar
[24] Murman S M 2005 43rd AIAA Aerospace Sciences Meeting Reno, NV, January 10−13, 2005 AIAA 2005-0840
[25] Hassan D, Sicot F 2011 49th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition Orlando, Florida, January 4−7, 2011 AIAA 2011-1242
[26] 陈琦, 陈坚强, 袁先旭, 谢昱飞 2014 力学学报 46 183
Google Scholar
Chen Q, Chen J Q, Yuan X X, Xie Y F 2014 Chinese Journal of Theoretical and Applied Mechanics 46 183
Google Scholar
[27] 柴振霞, 刘伟, 刘绪, 杨小亮 2018 国防科技大学学报 40 30
Google Scholar
Chai Z X, Liu W, Liu X, Yang X L 2018 J. Nat. Univ. Defense Technol. 40 30
Google Scholar
[28] Clark E B, Ekici K, Beran P S 2014 44th AIAA Fluid Dynamics Conference Atlanta, GA, June 16−20, 2014 AIAA 2014-3323
[29] Cvijetic G, Jasak H, Vukcevic V 2016 54th AIAA Aerospace Sciences Meetin San Diego, California, USA, January 4−8, 2016 AIAA 2006-0070
[30] McMullen M, Jameson A, Alonso J J 2002 40th AIAA Aerospace Sciences Meeting & Exhibit Reno, NV, January 14−17, 2002 AIAA 2002-0120
[31] Gopinath A K, Jameson A 2006 44th AIAA Aerospace Sciences Meeting and Exhibit Reno, Nevada, January 9−12, 2006 AIAA 2006-449
[32] Spiker M A, Thomas J P, Hall K C, Kielb R E, Dowell E H 2006 47th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference Newport, Rhode Island, May 1−4, 2006 AIAA 2006-1965
[33] Mosahebi A, Nadarajah S K 2010 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition Orlando, Florida, January 4−7, 2010 AIAA 2010-1267
[34] Yao W, Jaiman R K 2016 J. Fluids Struct. 65 313
Google Scholar
[35] Yao W, Marques S 2015 AIAA J. 53 2040
Google Scholar
[36] 张炜, 席光 2009 西安交通大学学报 43 114
Google Scholar
Zhang W, Xi G 2009 Journal of Xi'an Jiaotong University 43 114
Google Scholar
[37] Jameson A 1991 10th Computational Fluid Dynamics Conference Honolulu, HI, June 24−26, 1991 AlAA 1991-1596
[38] Landon R H 1982 NACA 0012 Oscillatory and Transient Pitching Tech. Rep. AGARD-R-702
[39] Batina J T 1990 AIAA J. 28 1381
Google Scholar
[40] Henderson R D 1995 Phys. Fluids 7 2102
Google Scholar
[41] Wieselsberger C 1922 Physik. Z. 22 321
[42] Roshko A 1954 On the Development of Turbulent Wakes From Vortex Streets (California Institute of Technology, NACA) Tech. Rep. 1191
[43] Williamson C H K 1988 Phys. Fluids 31 2742
Google Scholar
[44] Williamson C H K 1998 J. Fluids Struct. 12 1073
Google Scholar
[45] 张宝林 2005 最优化理论与算法 (北京: 清华大学出版社)
Zhang B L 2005 Theory and Algorithms of Optimization (Beijing: Tsinghua University Press) (in Chinese)
[46] Sohankar A, Davidson L, Norberg C 1995 Twelfth Australaian Fluid Mechanics Conference Sydney, Australia, December, 199 p517
DownLoad:
Catalog
Metrics
- Abstract views: 10018
- PDF Downloads: 74
- Cited By: 0
