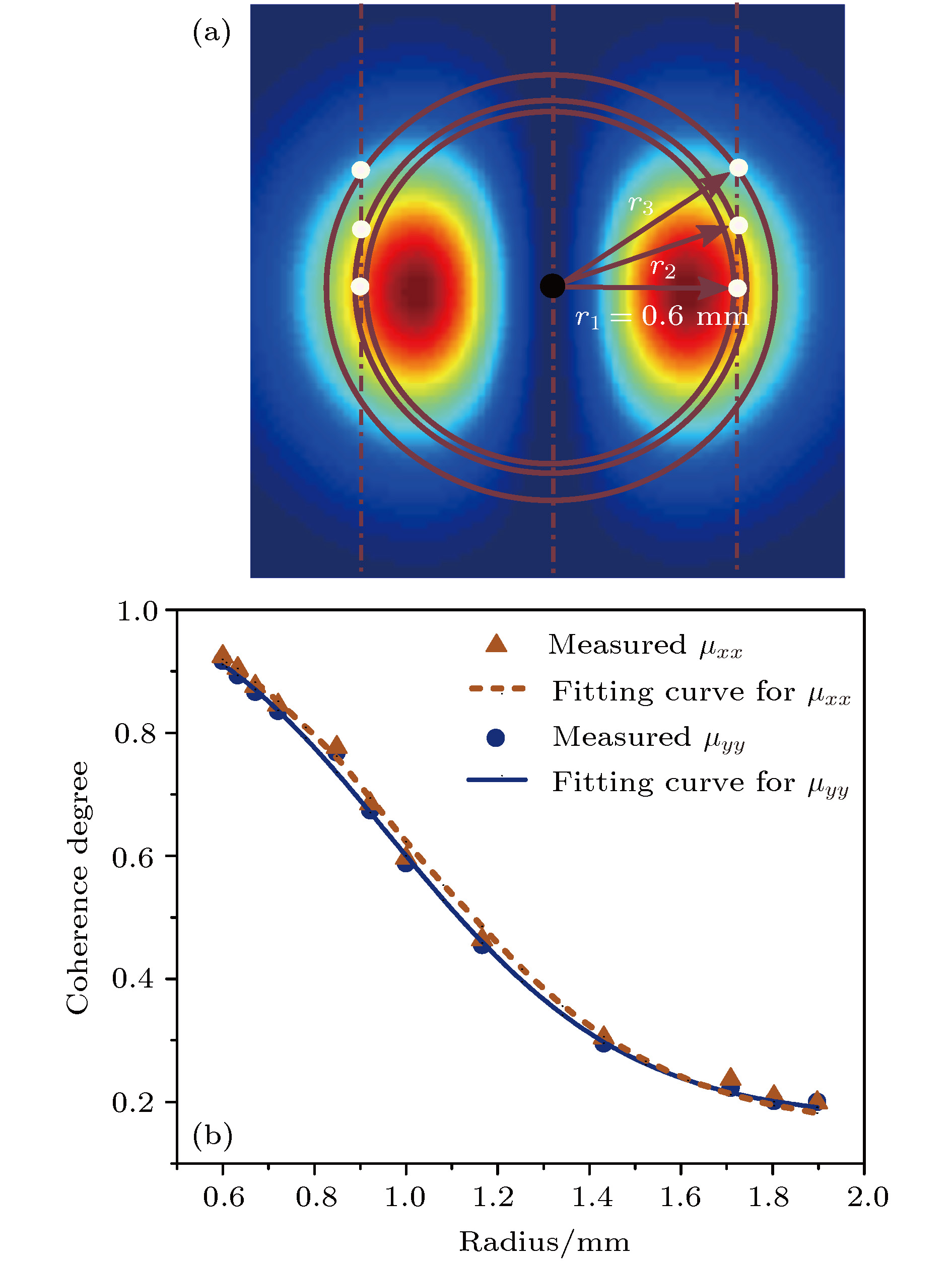
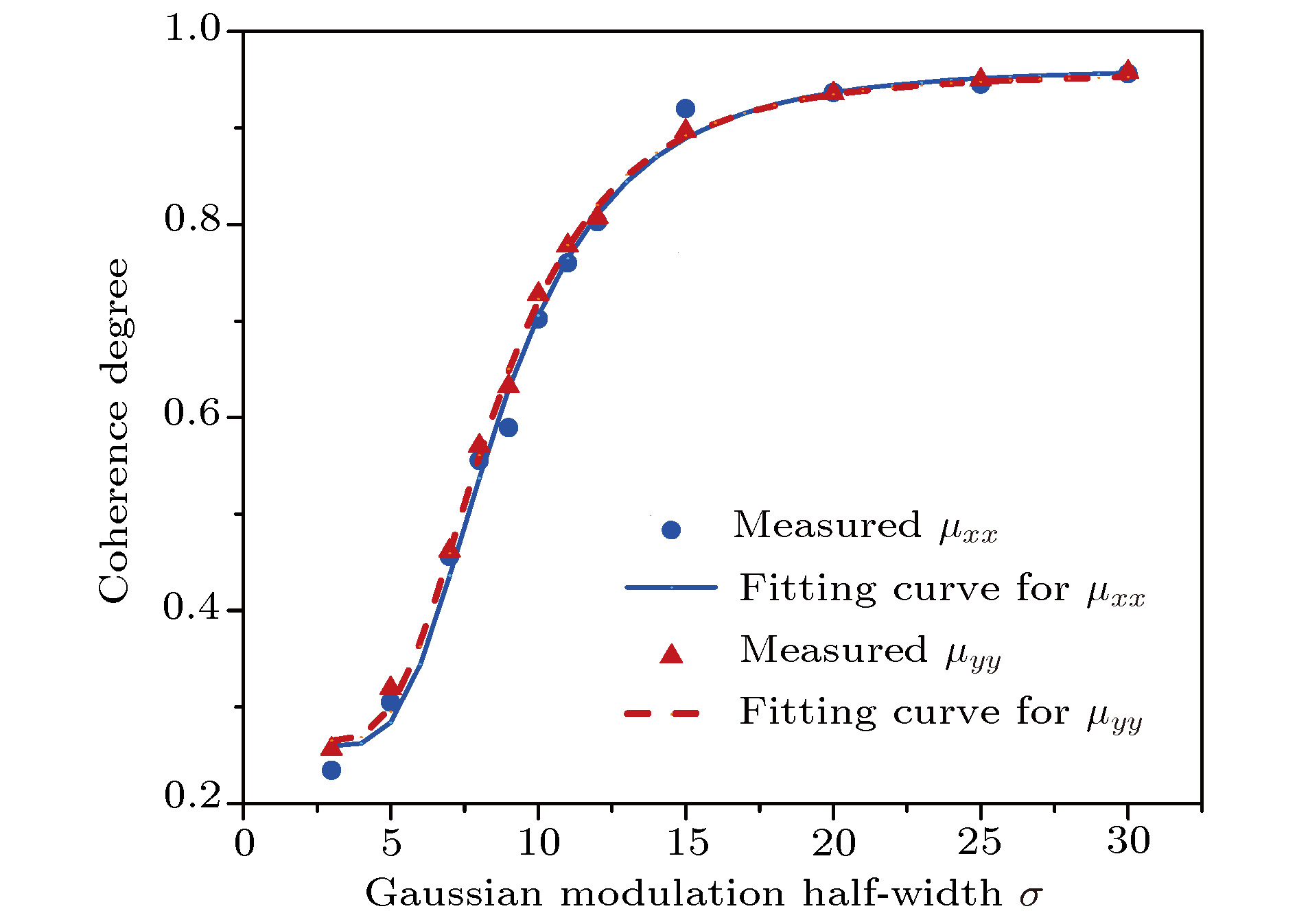
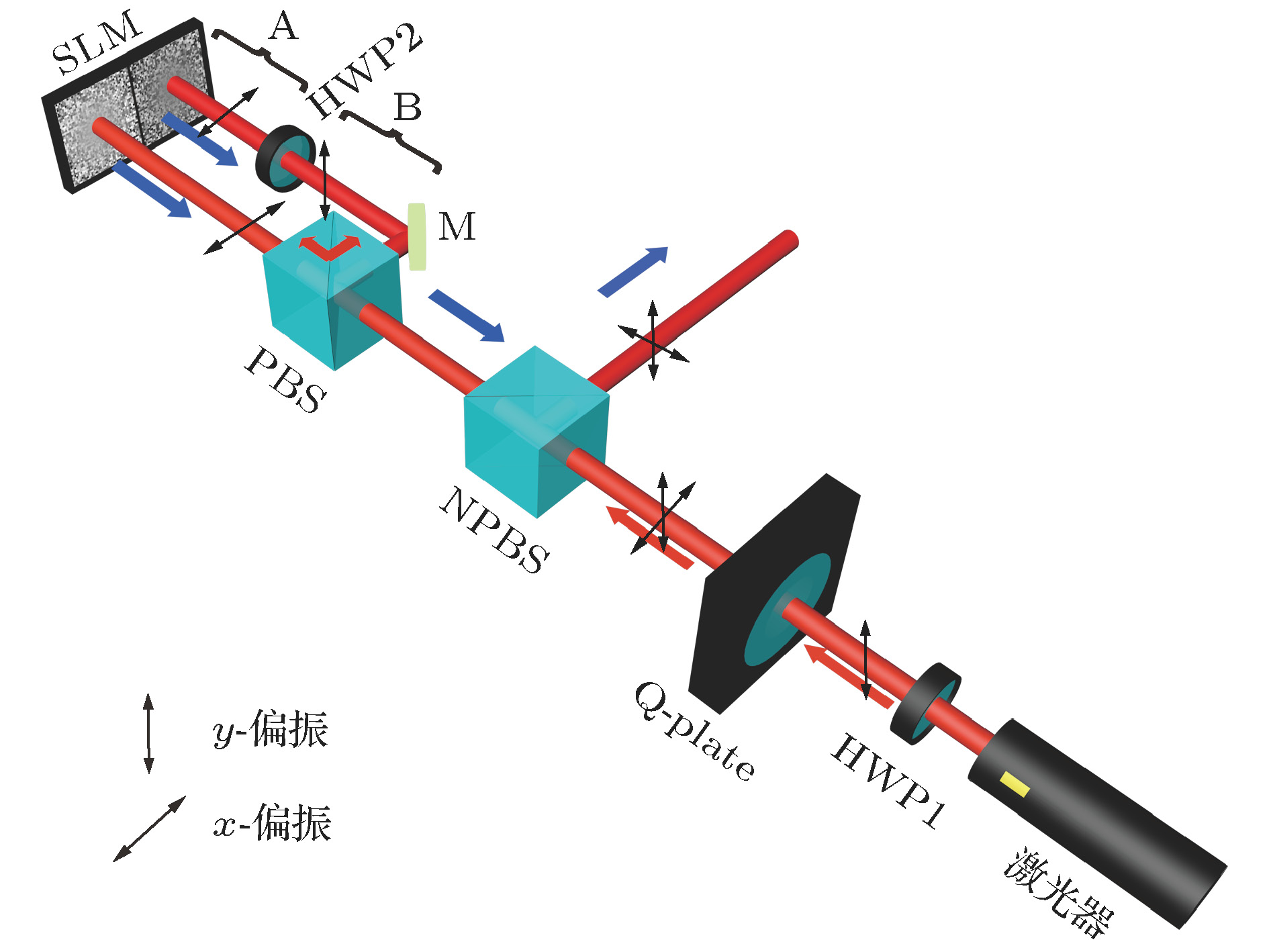
-
Since the unified theory of coherence and polarization for partially coherent vector beams was proposed by Gori and Wolf, the characterization, generation and propagation of partially coherent vector beams have been extensively studied. During the last decade, partially coherent vector beams with non-uniform polarization, also referred to as cylindrical vector partially coherent beams, have gained more and more attention. It was found that the intensity profile of focused azimuthally/radially polarized beam could be shaped by varying its initial spatial coherence. This characteristic may have potential applications in material thermal processing and particle trapping. Until now, there have been several reports concerning the generation of cylindrical vector partially coherent beams. However, in most of these reports a ground-glass diffuser was used, which generally restricts the generation of shell-model sources. In this paper, we theoretically and experimentally investigate the generation of radially polarized partially coherent beams with non-uniform correlation. According to the relation between phase correlation and optical coherence, we theoretically investigate the 2 × 2 cross-spectral density matrix and the coherence distribution of our generated non-uniformly correlated radially polarized partially coherent beams. In experiment, we generate dynamic random phase patterns with uniform distribution in time and inverse Gaussian distribution in space. A complete coherent radially polarized beam is divided into two parts by a polarizing beam splitter, i.e., the transmitted x-polarization component (HG10 beam) and the reflected y-polarization component (HG01 beam). The two orthogonally polarized components are respectively modulated with the two halves of a single phase-only liquid crystal spatial light modulator, thus generating a radially polarized partially coherent beam. We measure the correlation distribution of the generated beam in Young’s two-pinhole experiment. It is shown that the experimental observations are in agreement with our theoretical analyses. The generated partially coherent beam has an un-uniform correlation structure, and its coherence degree may be controlled by varying the Gaussian modulation half-width of the random phase. Our experimental results have also shown that the intensity profile of the radially polarized partially coherent beam can be modulated with the Gaussian modulation half-width. With the increase of Gaussian modulation half-widths and the gradual decrease of coherence degree, the intensity profile gradually transforms from a dark hollow beam profile into a flat-topped-like beam profile. The radially polarized partially coherent beams with non-uniform correlation may have some applications in optical manipulation and material thermal processing.
-
Keywords:
- non-uniformly correlated /
- radially polarized beam /
- cylindrical vector partially coherent beam /
- spatial coherence
[1] Mandel L, Wolf E 1995 Optical Coherence and Quantum Optics (Cambridge: Cambridge University Press) pp340―373
[2] Zhan Q W 2009 Adv. Opt. Photon. 1 1
Google Scholar
[3] Naidoo D, Roux F S, Dudley A, Litvin I, Piccirillo B, Marrucci L, Forbes A 2016 Nat. Photonics 10 327
Google Scholar
[4] Lin H C, Zhou X M, Chen Z Y, Sasaki O, Li Y, Pu J X 2018 J. Opt. Soc. Am. A 35 1974
Google Scholar
[5] Wolf E 2007 Introduction to the Theory of Coherence and Polarization of Light (Cambridge: Cambridge University Press) pp 174―179
[6] Zhan Q W 2014 Vectorial Optical Fields: Fundamentals and Applications (Hackensack New Jersey: World Scientific) pp 221―277
[7] Ostrovsky A S, Rodriguez-Zurita G, Meneses-Fabian C, Olvera-Santamaria M A, Rickenstorff-Parrao C 2010 Opt. Express 18 12864
Google Scholar
[8] Zhang Y T, Cui Y, Wang F, Cai Y J 2015 Opt. Express 23 11483
Google Scholar
[9] Guo M W, Zhao D M 2018 Opt. Express 26 8581
Google Scholar
[10] Cai Y J, Korotkova O, Eyyuboglu H T, Baykal Y 2008 Opt. Express 16 15834
Google Scholar
[11] Mei Z R, Korotkova O, Shchepakina E 2013 J. Opt. 15 025705
Google Scholar
[12] Liang C H, Wang F, Liu X L, Cai Y J, Korotkova O 2014 Opt. Lett. 39 769
Google Scholar
[13] Tong Z S, Korotkova O 2012 J. Opt. Soc. Am. A 29 2154
Google Scholar
[14] Cai Y J, Chen Y H, Wang F 2014 J. Opt. Soc. Am. A 31 2083
Google Scholar
[15] 张磊, 陈子阳, 崔省伟, 刘绩林, 蒲继雄 2015 64 034205
Google Scholar
Zhang L, Chen Z Y, Cui S W, Liu J L, Pu J X 2015 Acta Phys. Sin. 64 034205
Google Scholar
[16] Gu Y L, Gbur G 2013 Opt. Lett. 38 1395
Google Scholar
[17] Dong Y M, Cai Y J, Zhao C L, Yao M 2011 Opt. Express 19 5979
Google Scholar
[18] Dong Y M, Wang F, Zhao C L, Cai Y J 2012 Phys. Rev. A 86 324
Google Scholar
[19] Wang F, Liu X L, Liu L, Yuan Y S, Cai Y J 2013 Appl. Phys. Lett. 103 91102
Google Scholar
[20] Zhu S J, Chen Y H, Wang J, Wang H Y, Li Z H, Cai Y J 2015 Opt. Express 23 33099
Google Scholar
[21] Luo Y M, Lü B D 2010 J. Opt. 12 115703
Google Scholar
[22] Lin H C, Pu J X 2009 J. Mod. Opt. 56 1296
Google Scholar
[23] Wang F, Cai Y J, Dong Y M, Korotkova O 2012 Appl. Phys. Lett. 100 51108
Google Scholar
[24] Wu G F, Wang F, Cai Y J 2012 Opt. Express 20 28301
Google Scholar
[25] Cui S W, Chen Z Y, Zhang L, Pu J X 2013 Opt. Lett. 38 4821
Google Scholar
[26] Chen X D, Chang C C, Chen Z Y, Lin Z L, Pu J X 2016 Opt. Express 24 21587
Google Scholar
[27] 昌成成, 蒲继雄, 陈子阳, 陈旭东 2017 66 054212
Google Scholar
Chang C C, Pu J X, Chen Z Y, Chen X D 2017 Acta Phys. Sin. 66 054212
Google Scholar
[28] Tervo J, Setala T, Friberg A T 2012 Opt. Lett. 37 151
Google Scholar
[29] Zhang B, Chu X L, Li Q 2002 J. Opt. Soc. Am. A 19 1370
Google Scholar
[30] Ji X L, Zhang T R, Jia X H 2009 J. Opt. A: Pure Appl. Opt. 11 105705
Google Scholar
[31] Zhou G Q 2009 J. Opt. A: Pure Appl. Opt. 12 015701
Google Scholar
[32] Zhang Y J, Ding B F, Suyama T 2010 Phys. Rev. A 81 109
Google Scholar
[33] Zhao C L, Cai Y J 2011 Opt. Lett. 36 2251
Google Scholar
-
图 1 产生非均匀关联径向偏振部分相干光的光路示意图
Figure 1. An optical arrangement for producing partially coherent radially polarized beam with non-uniform correlation
图 2 动态相位图样的一帧图样, 高斯调制半宽
${\sigma }$ = 20 (即${\sigma _x}$ =${\sigma _y}$ = 20)Figure 2. One frame of dynamic phase patterns. Both the left pattern and the right one are generated with
${\sigma }$ = 20 (i.e.${\sigma _x}$ =${\sigma _y}$ = 20)
图 3 (a)利用杨氏-双孔干涉实验测量相干度的原理图; (b)相干度的测量结果
Figure 3. (a) The schematics for measuring the coherence degree by two-pinhole interference experiment; (b) experimental resuls and fitting results of coherence degree
图 4 不同调制半宽的动态随机相位图的一帧 (a)
${\sigma }$ = ∞; (b)${\sigma }$ = 15; (c)${\sigma }$ = 10; (d)${\sigma }$ = 3Figure 4. One frame of dynamic phase patterns with different Gaussian modulaton half-widths: (a)
${\sigma }$ = ∞; (b)${\sigma }$ = 15; (c)${\sigma }$ = 10; (d)${\sigma }$ = 3
图 5 两个小孔位置之间的相干度随高斯调制半宽
${\sigma }$ 变化的曲线Figure 5. Experimental results of coherence degree between two fixed points as a function of
${\sigma }$ 
图 6 光束质量因子M2随高斯调制半宽
${\sigma }$ 变化的曲线Figure 6. Experimental results of M2 as a function of
${\sigma }$ 
图 7 不同调制半宽度下的部分相干径向偏振光的光强分布图样 (a)
${\sigma }$ = ∞; (b)${\sigma }$ = 15; (c)${\sigma }$ = 10; (d)${\sigma }$ = 3Figure 7. Intensity distributions of partially coherent radially polarized beams generated with different
${\sigma }$ : (a)${\sigma }$ = ∞; (b)${\sigma }$ = 15; (c)${\sigma }$ = 10; (d)${\sigma }$ = 3
图 8 不同调制半宽度下径向偏振部分相干光经过0°偏振片后的光斑图样 (a)
${\sigma }$ = ∞; (b)${\sigma }$ = 15; (c)${\sigma }$ = 10; (d)${\sigma }$ = 3Figure 8. Intensity profiles of partially coherent radially polarized beams with different
${\sigma }$ after passing through a linear polarizer with a transmission angle of 0°: (a)${\sigma }$ = ∞; (b)${\sigma }$ = 15; (c)${\sigma }$ = 10; (d)${\sigma }$ = 3
图 9 不同调制半宽度下径向偏振部分相干光经过90°偏振片后的光斑图样 (a)
${\sigma }$ = ∞; (b)${\sigma }$ = 15; (c)${\sigma }$ = 10; (d)${\sigma }$ = 3Figure 9. Intensity profiles of partially coherent radially polarized beams with different
${\sigma }$ after passing through a linear polarizer with a transmission angle of 90°: (a)${\sigma }$ = ∞; (b)${\sigma }$ = 15; (c)${\sigma }$ = 10; (d)${\sigma }$ = 3 -
[1] Mandel L, Wolf E 1995 Optical Coherence and Quantum Optics (Cambridge: Cambridge University Press) pp340―373
[2] Zhan Q W 2009 Adv. Opt. Photon. 1 1
Google Scholar
[3] Naidoo D, Roux F S, Dudley A, Litvin I, Piccirillo B, Marrucci L, Forbes A 2016 Nat. Photonics 10 327
Google Scholar
[4] Lin H C, Zhou X M, Chen Z Y, Sasaki O, Li Y, Pu J X 2018 J. Opt. Soc. Am. A 35 1974
Google Scholar
[5] Wolf E 2007 Introduction to the Theory of Coherence and Polarization of Light (Cambridge: Cambridge University Press) pp 174―179
[6] Zhan Q W 2014 Vectorial Optical Fields: Fundamentals and Applications (Hackensack New Jersey: World Scientific) pp 221―277
[7] Ostrovsky A S, Rodriguez-Zurita G, Meneses-Fabian C, Olvera-Santamaria M A, Rickenstorff-Parrao C 2010 Opt. Express 18 12864
Google Scholar
[8] Zhang Y T, Cui Y, Wang F, Cai Y J 2015 Opt. Express 23 11483
Google Scholar
[9] Guo M W, Zhao D M 2018 Opt. Express 26 8581
Google Scholar
[10] Cai Y J, Korotkova O, Eyyuboglu H T, Baykal Y 2008 Opt. Express 16 15834
Google Scholar
[11] Mei Z R, Korotkova O, Shchepakina E 2013 J. Opt. 15 025705
Google Scholar
[12] Liang C H, Wang F, Liu X L, Cai Y J, Korotkova O 2014 Opt. Lett. 39 769
Google Scholar
[13] Tong Z S, Korotkova O 2012 J. Opt. Soc. Am. A 29 2154
Google Scholar
[14] Cai Y J, Chen Y H, Wang F 2014 J. Opt. Soc. Am. A 31 2083
Google Scholar
[15] 张磊, 陈子阳, 崔省伟, 刘绩林, 蒲继雄 2015 64 034205
Google Scholar
Zhang L, Chen Z Y, Cui S W, Liu J L, Pu J X 2015 Acta Phys. Sin. 64 034205
Google Scholar
[16] Gu Y L, Gbur G 2013 Opt. Lett. 38 1395
Google Scholar
[17] Dong Y M, Cai Y J, Zhao C L, Yao M 2011 Opt. Express 19 5979
Google Scholar
[18] Dong Y M, Wang F, Zhao C L, Cai Y J 2012 Phys. Rev. A 86 324
Google Scholar
[19] Wang F, Liu X L, Liu L, Yuan Y S, Cai Y J 2013 Appl. Phys. Lett. 103 91102
Google Scholar
[20] Zhu S J, Chen Y H, Wang J, Wang H Y, Li Z H, Cai Y J 2015 Opt. Express 23 33099
Google Scholar
[21] Luo Y M, Lü B D 2010 J. Opt. 12 115703
Google Scholar
[22] Lin H C, Pu J X 2009 J. Mod. Opt. 56 1296
Google Scholar
[23] Wang F, Cai Y J, Dong Y M, Korotkova O 2012 Appl. Phys. Lett. 100 51108
Google Scholar
[24] Wu G F, Wang F, Cai Y J 2012 Opt. Express 20 28301
Google Scholar
[25] Cui S W, Chen Z Y, Zhang L, Pu J X 2013 Opt. Lett. 38 4821
Google Scholar
[26] Chen X D, Chang C C, Chen Z Y, Lin Z L, Pu J X 2016 Opt. Express 24 21587
Google Scholar
[27] 昌成成, 蒲继雄, 陈子阳, 陈旭东 2017 66 054212
Google Scholar
Chang C C, Pu J X, Chen Z Y, Chen X D 2017 Acta Phys. Sin. 66 054212
Google Scholar
[28] Tervo J, Setala T, Friberg A T 2012 Opt. Lett. 37 151
Google Scholar
[29] Zhang B, Chu X L, Li Q 2002 J. Opt. Soc. Am. A 19 1370
Google Scholar
[30] Ji X L, Zhang T R, Jia X H 2009 J. Opt. A: Pure Appl. Opt. 11 105705
Google Scholar
[31] Zhou G Q 2009 J. Opt. A: Pure Appl. Opt. 12 015701
Google Scholar
[32] Zhang Y J, Ding B F, Suyama T 2010 Phys. Rev. A 81 109
Google Scholar
[33] Zhao C L, Cai Y J 2011 Opt. Lett. 36 2251
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7917
- PDF Downloads: 81
- Cited By: 0
