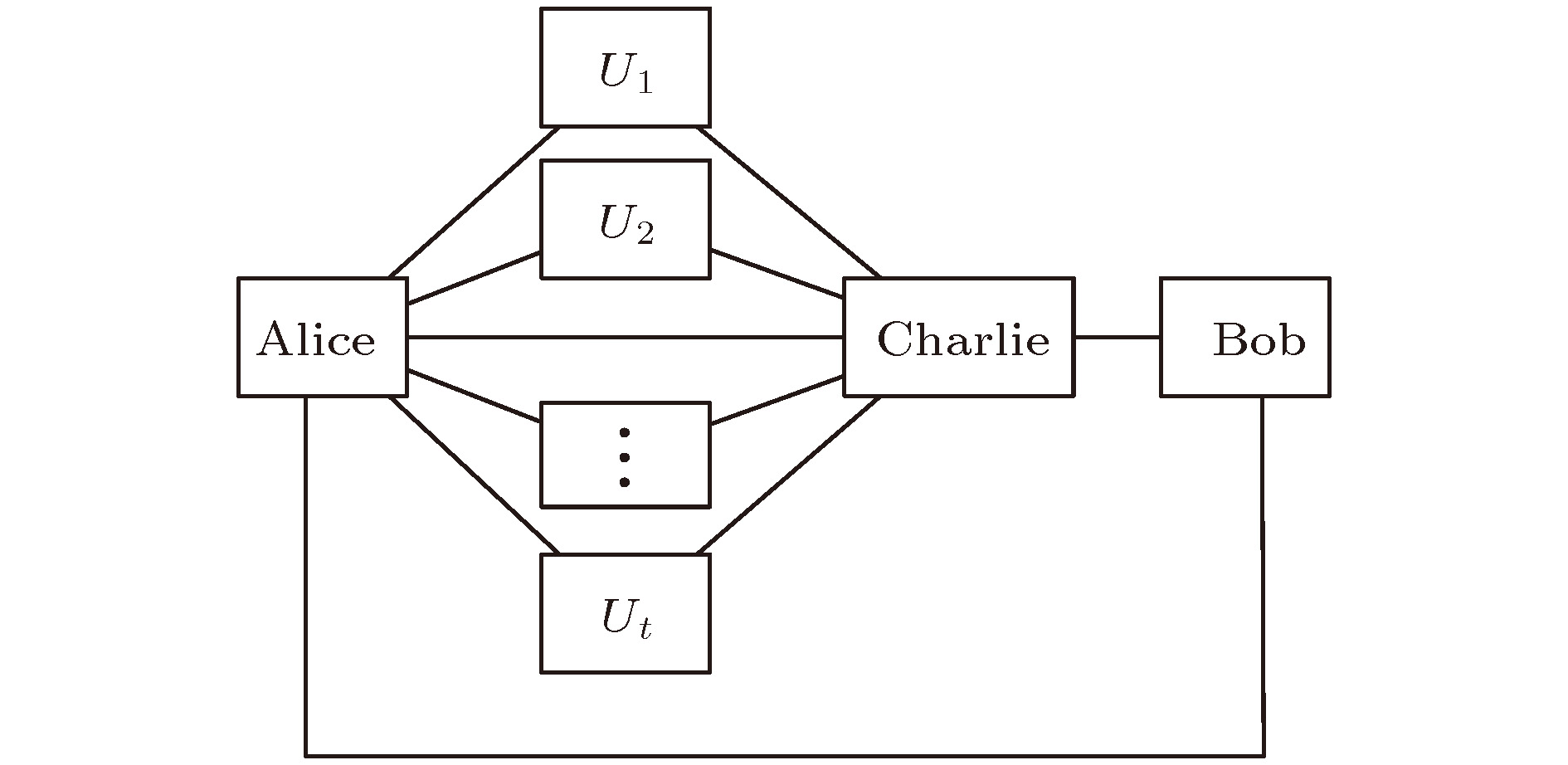
-
Recently, a quantum broadcasting multiple blind signature scheme based on GHZ state has been proposed, which could be used to settle the problem that a message is so important that it needs to be signed by multiple signatories, in order to guarantee the message privacy: none of signatories can acquire the content of the message they have signed. Maybe it can be applied to an E-bank system. For example, a large amount of money has to be transferred through E-bank system on the internet. The E-bank system operator submits the request to the bank after filling the application form including payment amount, bank transfer account and some other information. When the request arrives, the bank clerk signs to approve. However, it is not enough, it has to ask the manager for authority, and then it needs to be signed by the manager. In the whole process, all the signatories cannot learn what they have signed, but the application form has been recorded in the E-bank system. So, once disagreement takes place, the bank can track the message sender. In this paper, we present a new quantum broadcasting multiple blind signature scheme which is based on a three-particle partial entanglement state. Comparing with the original scheme, the partial entanglement state is utilized in our new scheme in place of the GHZ state, and this does not bring down the security of the scheme. Particularly, using the partial entanglement state can not only save the entanglement resource to some extent, but also make the scheme much easier to be realized. As is well known, It is not easy to keep the maximum entanglement state shared among the participants in the whole quantum communication process. By using the partial entanglement in place of the maximum entanglement can improve the new scheme applicability to make it more practical. It is also indicated that multi-qubit entangled systems which are partially entangled can be efficiently used as a resource in quantum information processing with perfect performance. -
Keywords:
- quantum broadcasting multiple blind signature scheme /
- three-particle partial entanglement state /
- hash function
[1] Shor P W 1994 Proceeding of IEEE Symposium on Foundations of Computer Science Santa Fe NM USA, November 20―22, 1994 p124
[2] Wallden P, Dunjko V, Kent A, et al. 2014 Phys. Rev. A 91 042304
[3] Amiri R, Andersson E 2015 Entropy 17 5635
Google Scholar
[4] Gottesman D, Chuang I 2001 arXiv:quant-ph/0105032v2
[5] Zeng G, Keitel C 2002 Phys. Rev. A 65 042312
Google Scholar
[6] Li Q, Chan W, Long D 2009 Phys. Rev. A 79 054307
Google Scholar
[7] Zou X, Qiu D 2010 Phys. Rev. A 82 042325
Google Scholar
[8] Yin X, Ma W, Liu W 2012 Int. J. Quantum Inf. 10 1250041
Google Scholar
[9] Wang T, Wei Z 2012 Quantum Inf. Process. 11 455
Google Scholar
[10] Yang Y 2008 Chin. Phys. B 17 415
Google Scholar
[11] Cao H, Huang J, Yu Y, et al. 2014 Int. J. Theor. Phys. 53 3095
Google Scholar
[12] Xu G 2015 Int. J. Theor. Phys. 54 2605
Google Scholar
[13] Wen X, Tian Y, Ji L, et al. 2010 Phys. Scr. 81 055001
Google Scholar
[14] Wen X 2010 Phys. Scr. 82 065403
Google Scholar
[15] Xu R, Huang L, Yang W, et al. 2011 Opt. Commun. 284 3654
Google Scholar
[16] Zhang K, Song T, Zuo H, et al. 2013 Phys. Scr. 87 045012
Google Scholar
[17] Xu G, Zhang K 2015 Quantum Inf. Process. 14 2577
Google Scholar
[18] Su Q, Huang Z, Wen Q, et al. 2010 Opt. Commun. 283 4408
Google Scholar
[19] Yin X, Ma W, Liu W 2012 Int. J. Theor. Phys. 51 455
Google Scholar
[20] Lin T, Chen Y, Chang T, et al. 2014 Proceeding of 2014 IEEE 14th International Conference on Nanotechnology Toronto Canada, August 18―21, 2014 p868
[21] Shi W, Zhang J, Zhou Y, et al. 2015 Quantum Inf. Process. 14 3019
Google Scholar
[22] Wen X, Liu Y, Sun Y 2007 Z. Naturforsch. A 62 147
[23] Wen X, Liu Y, Zhou N 2008 Int. J. Mod. Phys. B 22 4251
Google Scholar
[24] Wen X, Niu X, Ji L, et al. 2009 Opt. Commun. 282 666
Google Scholar
[25] Xiao M, Li Z 2016 Quantum Inf. Process. 15 3841
Google Scholar
[26] Tian Y, Chen H, Ji S, et al. 2014 Opt. Quant. Electron. 46 769
Google Scholar
[27] Zhang W, Qiu D, Zou X 2016 Quantum Inf. Process. 15 2499
Google Scholar
[28] Tian Y, Chen H, Gao Y, et al. 2014 Int. J. Mod. Phys.: Conf. Ser. 33 1460369
Google Scholar
[29] Zhang W, Qiu D, Zou X, et al. 2017 Quantum Inf. Process. 16 150
Google Scholar
[30] Kim T, Choi J, Jho N, et al. 2015 Phys. Scr. 90 025101
Google Scholar
[31] Yu C, Guo G, Lin S 2014 Sci. China Phys. Mech. Astron. 57 2079
Google Scholar
[32] Kumar A, Adhikari S, Banerjee S, Roy S 2013 Phys. Rev. A 87 022307
Google Scholar
-
图 1 量子广播多重盲签名协议的图示
Figure 1. The graph of quantum broadcasting multiple blind signature scheme.
-
[1] Shor P W 1994 Proceeding of IEEE Symposium on Foundations of Computer Science Santa Fe NM USA, November 20―22, 1994 p124
[2] Wallden P, Dunjko V, Kent A, et al. 2014 Phys. Rev. A 91 042304
[3] Amiri R, Andersson E 2015 Entropy 17 5635
Google Scholar
[4] Gottesman D, Chuang I 2001 arXiv:quant-ph/0105032v2
[5] Zeng G, Keitel C 2002 Phys. Rev. A 65 042312
Google Scholar
[6] Li Q, Chan W, Long D 2009 Phys. Rev. A 79 054307
Google Scholar
[7] Zou X, Qiu D 2010 Phys. Rev. A 82 042325
Google Scholar
[8] Yin X, Ma W, Liu W 2012 Int. J. Quantum Inf. 10 1250041
Google Scholar
[9] Wang T, Wei Z 2012 Quantum Inf. Process. 11 455
Google Scholar
[10] Yang Y 2008 Chin. Phys. B 17 415
Google Scholar
[11] Cao H, Huang J, Yu Y, et al. 2014 Int. J. Theor. Phys. 53 3095
Google Scholar
[12] Xu G 2015 Int. J. Theor. Phys. 54 2605
Google Scholar
[13] Wen X, Tian Y, Ji L, et al. 2010 Phys. Scr. 81 055001
Google Scholar
[14] Wen X 2010 Phys. Scr. 82 065403
Google Scholar
[15] Xu R, Huang L, Yang W, et al. 2011 Opt. Commun. 284 3654
Google Scholar
[16] Zhang K, Song T, Zuo H, et al. 2013 Phys. Scr. 87 045012
Google Scholar
[17] Xu G, Zhang K 2015 Quantum Inf. Process. 14 2577
Google Scholar
[18] Su Q, Huang Z, Wen Q, et al. 2010 Opt. Commun. 283 4408
Google Scholar
[19] Yin X, Ma W, Liu W 2012 Int. J. Theor. Phys. 51 455
Google Scholar
[20] Lin T, Chen Y, Chang T, et al. 2014 Proceeding of 2014 IEEE 14th International Conference on Nanotechnology Toronto Canada, August 18―21, 2014 p868
[21] Shi W, Zhang J, Zhou Y, et al. 2015 Quantum Inf. Process. 14 3019
Google Scholar
[22] Wen X, Liu Y, Sun Y 2007 Z. Naturforsch. A 62 147
[23] Wen X, Liu Y, Zhou N 2008 Int. J. Mod. Phys. B 22 4251
Google Scholar
[24] Wen X, Niu X, Ji L, et al. 2009 Opt. Commun. 282 666
Google Scholar
[25] Xiao M, Li Z 2016 Quantum Inf. Process. 15 3841
Google Scholar
[26] Tian Y, Chen H, Ji S, et al. 2014 Opt. Quant. Electron. 46 769
Google Scholar
[27] Zhang W, Qiu D, Zou X 2016 Quantum Inf. Process. 15 2499
Google Scholar
[28] Tian Y, Chen H, Gao Y, et al. 2014 Int. J. Mod. Phys.: Conf. Ser. 33 1460369
Google Scholar
[29] Zhang W, Qiu D, Zou X, et al. 2017 Quantum Inf. Process. 16 150
Google Scholar
[30] Kim T, Choi J, Jho N, et al. 2015 Phys. Scr. 90 025101
Google Scholar
[31] Yu C, Guo G, Lin S 2014 Sci. China Phys. Mech. Astron. 57 2079
Google Scholar
[32] Kumar A, Adhikari S, Banerjee S, Roy S 2013 Phys. Rev. A 87 022307
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7301
- PDF Downloads: 51
- Cited By: 0
