-
With the rapid development of computer network technology, information security has drawn considerable attention in recent years. Owing to the characteristics of multi-dimensional operation and parallel processing capability, optical image encryption techniques are arousing great interest in many exciting fields. Since the pioneering work on optical image encryption using double random phase encoding technique, a large number of algorithms and architectures have been proposed and realized. However, with the further analysis of the securities of these schemes, most of them have been verified to be vulnerable to different types of attack algorithms. Recently, optical encryption schemes based on the polarization properties of light wave have been extensively studied, for an additional flexibility in the encryption key design is provided, which can achieve high robustness against brute force attack by a combination of multiple private keys. Nevertheless, optical encryption schemes based on the polarization properties of light wave could still be vulnerable to known- and chosen- plaintext attacks. Therefore, in this paper, a novel asymmetric polarization encryption method is implemented for dual images, and combined with interference-based optical image encryption method and a Q-plate. First, the information about the two images to be encrypted is separated into two pure phase plates by means of interference optical image encryption, which will be further encoded into two mutually orthogonally polarized light beams. Next, the Q-plate and pixelated polarizer are used for realizing different polarization distributions of the two light beam. Ultimately, the output intensity distribution is recorded by a charge coupled device (CCD) which will be treated as the final ciphertext. For actualizing the asymmetric encryption, one of the pure phase plates acts as a decryption key, which is different from the encryption key. We can control the polarization state of each pixel according to the parameter q, causing the Q-plate to be electrically controllable and the optic-axis orientation of each pixel to differ from one another. It should be emphasized that the value of q and the polarization angle of the pixelated polarizer play the role of two encryption keys, which improves the security of the algorithm extremely, due to their high sensitiveness. Theoretical analyses and numerical simulations verify the feasibility and effectiveness of the proposed encryption scheme.
-
Keywords:
- Q-plate /
- asymmetric encryption /
- polarization
[1] Refregier P, Javidi B 1995 Opt. Lett. 20 767
Google Scholar
[2] Deng X P, Zhao D M 2012 Opt. Laser Technol. 44 136
Google Scholar
[3] Abuturab M R 2015 Opt. Lasers Eng. 69 49
Google Scholar
[4] Liu Z J, Guo C, Tan J B, Liu W, Wu J J, Wu Q, Pan L Q, Liu S T 2015 Opt. Lasers Eng. 68 87
Google Scholar
[5] Sui L S, Xin M T, Tian A L, Jin H Y 2013 Opt. Lasers Eng. 51 1297
Google Scholar
[6] Chen W, Chen X 2012 Appl. Opt. 51 6076
Google Scholar
[7] Rajput S K, Nishchal N K 2013 Appl. Opt. 52 4343
Google Scholar
[8] Qin W, Peng X 2010 Opt. Lett. 35 118
Google Scholar
[9] Chen W, Chen X D 2011 Opt. Commun. 284 3913
Google Scholar
[10] Rajput S K, Nishchal N K 2012 Appl. Opt. 51 1446
Google Scholar
[11] Liu W, Liu Z J, Liu S T 2013 Opt. Lett. 38 1651
Google Scholar
[12] Wang X G, Zhao D M 2012 Opt. Commun. 285 1078
Google Scholar
[13] Rajput S K, Nishchal N K 2013 Appl. Opt. 52 871
Google Scholar
[14] Wang X G, Chen Y X, Dai C Q, Zhao D M 2013 Appl. Opt. 53 208
[15] Alfalou A, Brosseau C 2010 Opt. Lett. 35 2185
Google Scholar
[16] Rajput S K, Nishchal N K 2012 Appl. Opt. 51 5377
Google Scholar
[17] Wang Q, Guo Q, Zhou J Y 2013 Appl. Opt. 52 8854
Google Scholar
[18] Cai J J, Shen X J, Lei M 2017 Opt. Commun. 403 211
Google Scholar
[19] Wang Q, Xiong D, Alfalou A, Brosseau C 2018 Opt. Commun. 415 56
Google Scholar
[20] Fatima A, Nishchal N K 2018 Opt. Commun. 417 30
Google Scholar
[21] Zhou J X, Liu Y C, Ke Y G, Luo H L, Wen S C 2015 Opt. Lett. 40 3193
Google Scholar
[22] Marrucci L, Manzo C, Paparo D 2006 Rev. Lett. 96 163905
Google Scholar
[23] Yi X N, Ling X H, Zhang Z Y, Li Y, Zhou X X, Liu Y C, Chen S Z, Luo H L, Wen S C 2014 Opt. Express 22 17207
Google Scholar
[24] Zhan Q W 2009 Adv. Opt. Photonics 1 1
Google Scholar
[25] Hasman E, Kleiner V, Biener G, Niv A 2003 Appl. Phys. Lett. 82 328
Google Scholar
[26] Niv A, Biener G, Kleiner V, Hasman E 2005 Opt. Lett. 30 2933
Google Scholar
[27] Zhang Y, Wang B 2008 Opt. Lett. 33 2443
Google Scholar
-
图 1 当q为0.5时的结构化示意图 ((x, y)代表笛卡尔坐标, 黄色虚线代表子波长槽,
$\alpha $ 表示局部光轴的方向)Figure 1. Structural diagram when q is 0.5 ((x, y) represents Cartesian coordinates; yellow dashed line represents subwavelength scale;
$\alpha $ represents local optical axes).
图 2 加密流程图
Figure 2. Flowcharts of encryption.
图 3 加密算法的模拟结果 (a), (b)原图1和原图2; (c)密文图像; (d)加密密钥
$\theta _{{\rm{rand}}}^{\left( {u,v} \right)}$ ; (e)解密密钥${\varphi _2}$ ; (f), (g)解密得到的两幅图像Figure 3. Simulation result of encryption algorithm: (a), (b) Original image of Lena and library; (c) ciphertext image; (d) encryption key
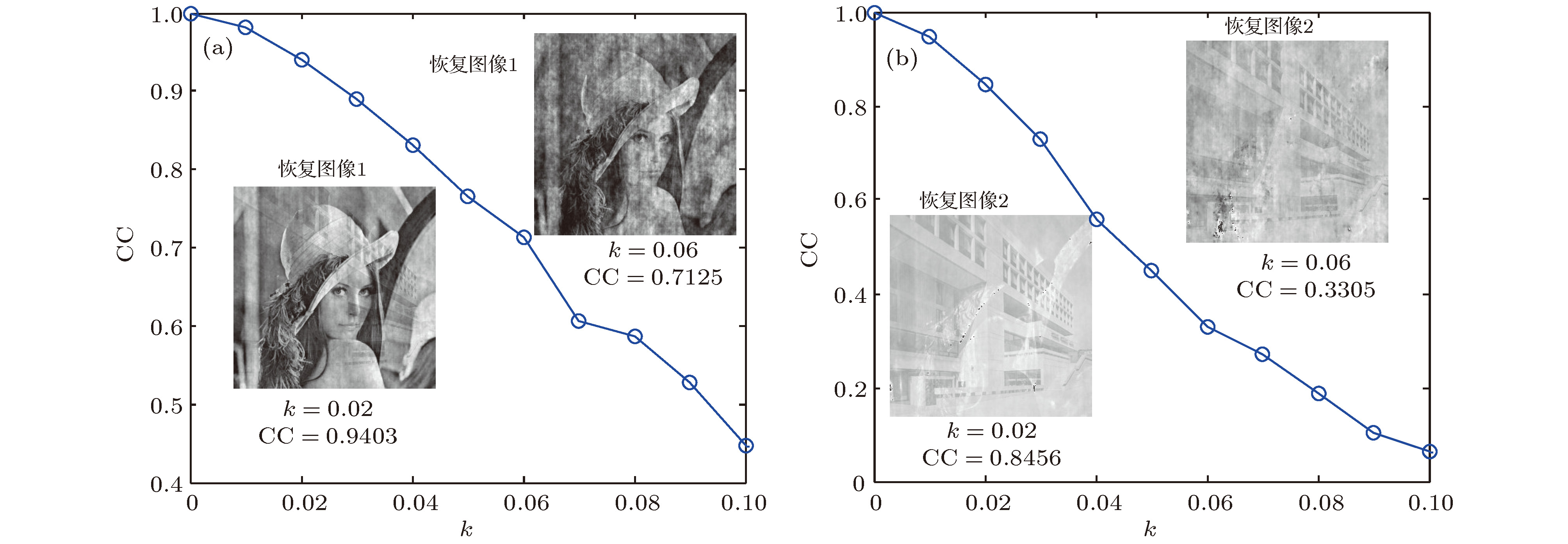
$\theta _{{\rm{rand}}}^{\left( {u,v} \right)}$ ; (e) decryption key; (f), (g) decrypted image.
图 4 加密密钥q加上0.0001时的解密图像 (a)解密图像1; (b)解密图像2
Figure 4. Decrypted image when the encryption key q is added with 0.0001: (a) Decrypted image 1; (b) decrypted image 2.
图 5 加密密钥
$\theta $ 增加了0.0001倍后的解密图像 (a)解密图像1; (b)解密图像2Figure 5. Decrypted image when the encryption key
$\theta $ is add with 0.0001 times: (a) Decrypted image 1; (b) decrypted image 2.
图 6 抗剪切攻击模拟结果图 (a)信息丢失6.25%的密文图; (b), (c)密文信息丢失6.25%后的解密图; (d)信息丢失25%的密文图; (e), (f)密文信息丢失25%的解密图
Figure 6. Simulation t diagram of anti-shear attack: (a) Ciphertext with 6.25% occlusion; (b), (c) decrypted images from (a); (d) 25% occlusion; (e), (f) decrypted images from (d).
图 7 抗噪声攻击模拟图 (a)第一幅解密图的相关系数CC随k变化的曲线图及k = 0.02, 0.06时的解密图; (b)第二幅解密图的相关系数CC随k变化的曲线图及k = 0.02, 0.06时的解密图
Figure 7. Simulation diagram of anti-noise attack: (a) CC curve of noise attack including decrypted the first image obtained with k = 0.02, 0.06; (b) CC curve of noise attack including decrypted the second image obtained with k = 0.02, 0.06.
图 8 传统偏振加密和使用Q-plate做偏振加密比较 (a)传统用波片做偏振加密, 加密密钥波片角度改变万分之一后的解密图; (b), (c)用Q-plate做偏振加密, 密钥q值改变万分之一后的解密图
Figure 8. Traditional polarization encryption compared with polarization encryption utilizing a q-plate: (a) Decryption image of traditional polarization encryption employing wave plates with the angle changed by 1/10000; (b), (c) decryption image of polarization encryption employing a Q-plate with the parameter q changed by 1/10000.
图 9 使用Q-plate做偏振加密和传统偏振加密比较 (a)用Q-plate做偏振加密, 信息丢失6.25%的密文图; (b), (c)用Q-plate做偏振加密, 密文信息丢失6.25%的解密图; (d)传统偏振加密, 信息丢失6.25%的密文图; (e)传统偏振加密, 信息丢失6.25%的解密图
Figure 9. Polarization encryption utilizing a q-plate compared with traditional polarization encryption: (a) Ciphertext with 6.25% occlusion of polarization encryption employing a Q-plate; (b), (c) decrypted image from (a); (d) ciphertext with 6.25% occlusion of traditional polarization encryption; (e) decrypted image from (d).
-
[1] Refregier P, Javidi B 1995 Opt. Lett. 20 767
Google Scholar
[2] Deng X P, Zhao D M 2012 Opt. Laser Technol. 44 136
Google Scholar
[3] Abuturab M R 2015 Opt. Lasers Eng. 69 49
Google Scholar
[4] Liu Z J, Guo C, Tan J B, Liu W, Wu J J, Wu Q, Pan L Q, Liu S T 2015 Opt. Lasers Eng. 68 87
Google Scholar
[5] Sui L S, Xin M T, Tian A L, Jin H Y 2013 Opt. Lasers Eng. 51 1297
Google Scholar
[6] Chen W, Chen X 2012 Appl. Opt. 51 6076
Google Scholar
[7] Rajput S K, Nishchal N K 2013 Appl. Opt. 52 4343
Google Scholar
[8] Qin W, Peng X 2010 Opt. Lett. 35 118
Google Scholar
[9] Chen W, Chen X D 2011 Opt. Commun. 284 3913
Google Scholar
[10] Rajput S K, Nishchal N K 2012 Appl. Opt. 51 1446
Google Scholar
[11] Liu W, Liu Z J, Liu S T 2013 Opt. Lett. 38 1651
Google Scholar
[12] Wang X G, Zhao D M 2012 Opt. Commun. 285 1078
Google Scholar
[13] Rajput S K, Nishchal N K 2013 Appl. Opt. 52 871
Google Scholar
[14] Wang X G, Chen Y X, Dai C Q, Zhao D M 2013 Appl. Opt. 53 208
[15] Alfalou A, Brosseau C 2010 Opt. Lett. 35 2185
Google Scholar
[16] Rajput S K, Nishchal N K 2012 Appl. Opt. 51 5377
Google Scholar
[17] Wang Q, Guo Q, Zhou J Y 2013 Appl. Opt. 52 8854
Google Scholar
[18] Cai J J, Shen X J, Lei M 2017 Opt. Commun. 403 211
Google Scholar
[19] Wang Q, Xiong D, Alfalou A, Brosseau C 2018 Opt. Commun. 415 56
Google Scholar
[20] Fatima A, Nishchal N K 2018 Opt. Commun. 417 30
Google Scholar
[21] Zhou J X, Liu Y C, Ke Y G, Luo H L, Wen S C 2015 Opt. Lett. 40 3193
Google Scholar
[22] Marrucci L, Manzo C, Paparo D 2006 Rev. Lett. 96 163905
Google Scholar
[23] Yi X N, Ling X H, Zhang Z Y, Li Y, Zhou X X, Liu Y C, Chen S Z, Luo H L, Wen S C 2014 Opt. Express 22 17207
Google Scholar
[24] Zhan Q W 2009 Adv. Opt. Photonics 1 1
Google Scholar
[25] Hasman E, Kleiner V, Biener G, Niv A 2003 Appl. Phys. Lett. 82 328
Google Scholar
[26] Niv A, Biener G, Kleiner V, Hasman E 2005 Opt. Lett. 30 2933
Google Scholar
[27] Zhang Y, Wang B 2008 Opt. Lett. 33 2443
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 8625
- PDF Downloads: 112
- Cited By: 0
