Search for Majorana zero mode in the magnetic vortex of artificial topological superconductor

Li Yao-Yi; Jia Jin-Feng

doi:10.7498/aps.68.20181698

Abstract

The search for new states that exhibit topological order is currently a very active and exciting area of research. Like a topological insulator, superconducting order can also exhibit topological order, which is different from that of a conventional superconductor. This superconductor is so-called " topological superconductor”, which has a full pairing gap in the bulk and gapless surface state. Majorana Fermions obey non-Abelian fractional statistics, and have been proposed to construct topological qubits, so there is a great prospect of scientific research and application in topological quantum computing. It is very interesting that Majorana Fermions are predicted to exist in topological superconductors. However, natural topological superconductor is very rare. Inspired by the realization of topological insulators, theoretical physicists have proposed that via the fabrication of the s-wave superconductor/topological insulator heterostructure, Majorana Fermions may exist in the superconducting topological insulator induced by proximate effect. Due to various kinds of topological insulators and conventional s-wave superconductors, heterostructures constructed by this method can greatly increase the variety of artificial topological superconductors. In this paper we review the experimental progress in the heterostructure composed of the Bi₂Te₃-type topological insulator and the conventional s-wave superconductor NbSe₂. Using molecular beam epitaxy, atomically flat topological insulator film can be fabricated at the top of superconductor substrate. The spatial distribution of Majorana Fermions on the surface of topological insulator can be directly observed by in situ scanning tunneling microscopy/spectroscopy. In the center of a magnetic vortex, Majorana Fermions will appear as the Majorana zero mode, a zero-energy peak inside the superconducting gap. Although the energy gap between low energy quasiparticle excitation and the Majorana zero mode is very small, the evidences such as zero bias conductance anomaly, Y-shape splitting of zero-bias conductance, spin-selective Andreev reflection are self-consistent and reveal that the Majorana zero mode exists in the center of a magnetic vortex. These experiments have led to a new insight into superconductivity. It may open a door to probing the novel physics of Majorana fermions.

Keywords:

proximity effects /
superconducting films and low-dimensional structures /
vortex phases /
tunneling phenomena

Authors and contacts

Li Yao-Yi^1,2,
Jia Jin-Feng^1,2

1.
Key Laboratory of Artificial Structures and Quantum Control (Ministry of Education), Shenyang National Laboratory for Materials Science, School of Physics and Astronomy, Shanghai Jiao Tong University, 800 Dongchuan Road, Shanghai 200240, China
2.
Tsung-Dao Lee Institute, Shanghai 200240, China

Corresponding author: Li Yao-Yi, yaoyili@sjtu.edu.cn ; Jia Jin-Feng, jfjia@sjtu.edu.cn

Funds: Project supported by the National Basic Research Program of China (Grant Nos. 2016YFA0301003, 2016YFA0300403), the National Natural Science Foundation of China (Grant Nos. 11521404, 11634009, U1632102, 11504230, 11674222, 11574202, 11674226, 11574201, U1632272, 11655002), and the Strategic Priority Research Program of Chinese Academy of Sciences, China (Grant No. XDB28000000).

FullText HTML : translate this paragraph

References

[1]	Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057 Google Scholar
[2]	Majorana E 1937 Nuovo Cimento 14 171 Google Scholar
[3]	Moore G, Read N 1991 Nucl. Phys. B 360 362 Google Scholar
[4]	Kitaev A 2003 Ann. Phys. 303 2 Google Scholar
[5]	Nayak C, Simon S H, Stern A, Freedman M, Das Sarma S 2008 Rev. Mod. Phys. 80 1083 Google Scholar
[6]	Wilczek F 2009 Nat. Phys. 5 614 Google Scholar
[7]	Alicea J 2012 Rep. Prog. Phys. 75 076501 Google Scholar
[8]	Beenakker C W J 2013 Annu. Rev. Condens. Mattter Phys. 4 113 Google Scholar
[9]	Leijnse M, Flensberg K 2012 Semicond. Sci. Technol. 27 124003 Google Scholar
[10]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[11]	Fu L, Kane C L 2008 Phys. Rev. Lett. 100 096407 Google Scholar
[12]	Ando Y 2013 J. Phys. Soc. Jpn. 82 102001 Google Scholar
[13]	Yu R, Zhang W, Zhang H J, Zhang S C, Dai X, Fang Z 2010 Science 329 61 Google Scholar
[14]	Chang C Z, Zhang J S, Feng X, Shen J, Zhang Z C, Guo M H, Li K, Ou Y B, Wei P, Wang L L, Ji Z Q, Feng Y, Ji S H, Chen X, Jia J F, Dai X, Fang Z, Zhang S C, He K, Wang Y Y, Lu L, Ma X C, Xue Q K 2013 Science 340 167 Google Scholar
[15]	Schnyder A P, Ryu S, Furusaki A, Ludwig A W W 2008 Phys. Rev. B 78 195125 Google Scholar
[16]	Linder J, Tanaka Y, Yokoyama T, Sudbo A, Nagaosa N 2010 Phys. Rev. Lett. 104 067001 Google Scholar
[17]	Hor Y S, Williams A J, Checkelsky J G, Roushan P, Seo J, Xu Q, Zandbergen H W, Yazdani A, Ong N P, Cava R J 2010 Phys. Rev. Lett. 104 057001 Google Scholar
[18]	Kriener M, Segawa K, Ren Z, Sasaki S, Ando Y 2011 Phys. Rev. Lett. 106 127004 Google Scholar
[19]	Sasaki S, Kriener M, Segawa K., Yada K, Tanaka Y, Sato M, Ando Y 2011 Phys. Rev. Lett. 107 217001 Google Scholar
[20]	Levy N, Zhang T, Ha J, Sharifi F, Alec Talin A, Kuk Y, Stroscio J A 2013 Phys. Rev. Lett. 110 117001 Google Scholar
[21]	Liu Z H, Yao X, Shao J F, Zuo M, Po L, Tan S, Zhang C J, Zhang Y H 2015 J. Am. Chem. Soc. 137 10512 Google Scholar
[22]	Maurya S V K, Neha P, Srivastava P, Patnaik S 2015 Phys. Rev. B 92 020506 Google Scholar
[23]	Lawson B J, Corbae P, Li G, Yu F, Asaba T, Tinsman C, Qiu Y, Medvedeva J E, Hor Y S, Li L 2016 Phys. Rev. B 94 041114 Google Scholar
[24]	Smylie M P, Claus H, Welp U, Kwok W K, Qiu Y, Hor Y S, Snezhko A 2016 Phys. Rev. B 94 180510 Google Scholar
[25]	Yonezawa S, Tajiri K, Nakata S, Nagai Y, Wang Z, Segawa K, Ando Y, Maeno Y 2017 Nat. Phys. 13 123 Google Scholar
[26]	Zhang J L, Zhang S J, Weng H M, Zhang W, Yang L X, Liu Q Q, Feng S M, Wang X C, Yu R C, Cao L Z, Wang L, Yang W G, Liu H Z, Zhao W Y, Zhang S C, Dai X, Fang Z, Jin C Q 2011 Proc. Natl. Acad. Sci. U.S.A. 108 24 Google Scholar
[27]	Zhang C, Sun L, Chen Z, Zhou X, Wu Q, Yi W, Guo J, Dong X, Zhao Z 2011 Phys. Rev. B 83 140504 Google Scholar
[28]	Kirshenbaum K, Syers P S, Hope A P, Butch N P, Jeffries J R, Weir S T, Hamlin J J, Maple M B, Vohra Y K, Paglione J 2013 Phys. Rev. Lett. 111 087001 Google Scholar
[29]	Zhu J, Zhang J L, Kong P P, Zhang S J, Yu X H, Zhu J L, Liu Q Q, Li X, Yu R C, Ahuja R, Yang W G, Shen G Y, Mao H K, Weng H M, Dai X, Fang Z, Zhao Y S, Jin C Q 2013 Sci. Rep. 3 2016 Google Scholar
[30]	Wang M X, Liu C H, Xu J P, Yang F, Miao L, Yao M Y, Gao C L, Shen C, Ma X C, Chen X, Xu Z A, Liu Y, Zhang S C, Qian D, Jia J F, Xue Q K 2012 Science 336 52 Google Scholar
[31]	Xu J P, Liu C H, Wang M X, Ge J F, Liu Z L, Yang X J, Chen Y, Liu Y, Xu Z A, Gao C L, Qian D, Zhang F C, Jia J F 2014 Phys. Rev. Lett. 112 217001 Google Scholar
[32]	Xu J P, Wang M X, Liu Z L, Ge J F, Yang X J, Liu C H, Xu Z A, Guan D D, Gao C L, Qian D, Liu Y, Wang Q H, Zhang F C, Xue Q K, Jia J F 2015 Phys. Rev. Lett. 114 017001 Google Scholar
[33]	Sun H H, Zhang K W, Hu L H, Li C, Wang G Y, Ma H Y, Xu Z A, Gao C L, Guan D D, Li Y Y, Liu C H, Qian D, Zhou Y, Fu L, Li S C, Zhang F C, Jia J F 2016 Phys. Rev. Lett. 116 257003 Google Scholar
[34]	Qu F, Yang F, Shen J, Ding Y, Chen J, Ji Z, Liu G, Fan J, Jing X, Yang C, Lu L 2012 Sci. Rep. 2 339 Google Scholar
[35]	Hart S, Ren H, Wagner T, Leubner P, Mühlbauer M, Brüne C, Buhmann H, Molenkamp L W, Yacoby A 2014 Nat. Phys. 10 638 Google Scholar
[36]	Knez I, Du R R, Sullivan G 2012 Phys. Rev. Lett. 109 186603 Google Scholar
[37]	Pribiag V S, Beukman A J A, Qu F, Cassidy M C, Charpentier C, Wegscheider W, Kouwenhoven L P 2015 Nat. Nanotechnol. 10 593 Google Scholar
[38]	He Q L, Pan L, Stern A L, Burks E C, Che X, Yin G, Wang J, Lian B, Zhou Q, Choi E S, Murata K, Kou X, Chen Z, Nie T, Shao Q, Fan Y, Zhang S C, Liu K, Xia J, Wang K L 2017 Science 357 294 Google Scholar
[39]	Mourik V, Zuo K, Frolov S M, Plissard S R, Bakkers E P A M, Kouwenhoven L P 2012 Science 336 1003 Google Scholar
[40]	Deng M T, Yu C L, Huang G Y, Larsson M, Caroff P, Xu H Q 2012 Nano Lett. 12 6414 Google Scholar
[41]	Nadj-Perge S, Drozdov I K, Li J, Chen H, Jeon S, Seo J, MacDonald A H, Bernevig B A, Yazdani A 2014 Science 346 602 Google Scholar
[42]	Koma A 1999 J. Cryst. Growth 201 236
[43]	Zhang H J, Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2009 Nat. Phys. 5 438 Google Scholar
[44]	Meerschaut A, Deudon C 2001 Mater. Res. Bull. 36 1721 Google Scholar
[45]	Zhang Y, He K, Chang C Z, Song C L, Wang L L, Chen X, Jia J F, Fang Z, Dai X, Shan W Y, Shen S Q, Niu Q, Qi X L, Zhang S C, Ma X C, Xue Q K 2010 Nat. Phys. 6 584 Google Scholar
[46]	Li Y Y, Wang G, Zhu X G, Liu M H, Ye C, Chen X, Wang Y Y, He K, Wang L L, Ma X C, Zhang H J, Dai X, Fang Z, Xie X C, Liu Y, Qi X L, Jia J F, Zhang S C, Xue Q K 2010 Adv. Mater. 22 4002 Google Scholar
[47]	Park K, Heremans J J, Scarola V W, Minic D 2010 Phys. Rev. Lett. 105 186801 Google Scholar
[48]	Liu Y, Bian G, Miller T, Bissen M, Chiang T C 2012 Phys. Rev. B 85 195442 Google Scholar
[49]	Black-Schaffer A M, Balatsky A V 2013 Phys. Rev. B 87 220506 Google Scholar
[50]	Tkachov G 2013 Phys. Rev. B 87 245422 Google Scholar
[51]	Xu S Y, Alidoust N, Belopolski I, Richardella A, Liu C, Neupane M, Bian G, Huang S H, Sankar R, Fang C, Dellabetta B, Dai W Q, Li Q, Gilbert M J, Chou F C, Samarth N, Hasan M Z 2014 Nat. Phys. 10 943 Google Scholar
[52]	Hess H F, Robinson R B, Dynes R C, Valles J M, Waszczak J V 1989 Phys. Rev. Lett. 62 214 Google Scholar
[53]	Eskildsen M R, Kugler M, Tanaka S, Jun J, Kazakov S M, Karpinski J, Fischer O 2002 Phys. Rev. Lett. 89 187003 Google Scholar
[54]	Sonier J E, Kiefl R F, Brewer J H, Chakhalian J, Dunsiger S R, MacFarlane W A, Miller R I, Wong A, Luke G M, Brill J W 1997 Phys. Rev. Lett. 79 1742 Google Scholar
[55]	Miller R I, Kiefl R F, Brewer J H, Chakhalian J, Dunsiger S, Morris G D, Sonier J E, MacFarlane W A 2000 Phys. Rev. Lett. 85 1540 Google Scholar
[56]	Chiu C K, Gilbert M J, Hughes T L 2011 Phys. Rev. B 84 144507 Google Scholar
[57]	Gygi F, Schluter M 1991 Phys. Rev. B 43 7609 Google Scholar
[58]	Kawakami T, Hu X 2015 Phys. Rev. Lett. 115 177001 Google Scholar
[59]	He J J, Ng T K, Lee P A, Law K T 2014 Phys. Rev. Lett. 112 037001 Google Scholar
[60]	Wiesendanger R 2009 Rev. Mod. Phys. 81 1495 Google Scholar
[61]	Hu L H, Li C, Xu D H, Zhou Y, Zhang F C 2016 Phys. Rev. B 94 224501 Google Scholar
[62]	Elliott S R, Franz M 2015 Rev. Mod. Phys. 87 137 Google Scholar
[63]	Kitaev A Y 2001 Phys. Usp. 44 131 Google Scholar
[64]	Law K T, Lee P A, Ng T K 2009 Phys. Rev. Lett. 103 237001 Google Scholar
[65]	Wimmer M, Akhmerov A R, Dahlhaus J P, Beenakker C W J 2011 New J. Phys. 13 053016 Google Scholar
[66]	Nilsson J, Akhmerov A R, Beenakker C W J 2008 Phys. Rev. Lett. 101 120403 Google Scholar
[67]	Fu L 2010 Phys. Rev. Lett. 104 056402 Google Scholar
[68]	Burnell F J, Shnirman A, Oreg Y 2013 Phys. Rev. B 88 224507 Google Scholar
[69]	Zhang P, Yaji K, Hashimoto T, Ota Y, Kondo T, Okazaki K, Wang Z, Wen J, Gu G D, Ding H, Shin S 2018 Science 360 182 Google Scholar
[70]	Wang D, Kong L, Fan P, Chen H, Zhu S, Liu W, Cao L, Sun Y, Du S, Schneeloch J, Zhong R, Gu G, Fu L, Ding H, Gao H J 2018 Science 362 333 Google Scholar
[71]	Liu Q, Chen C, Zhang T, Peng R, Yan Y J, Wen C H P, Lou X, Huang Y L, Tian J P, Dong X L, Wang G W, Bao W C, Wang Q H, Yin Z P, Zhao Z X, Feng D L 2018 Phys. Rev. X 8 041056 Google Scholar

Cited By

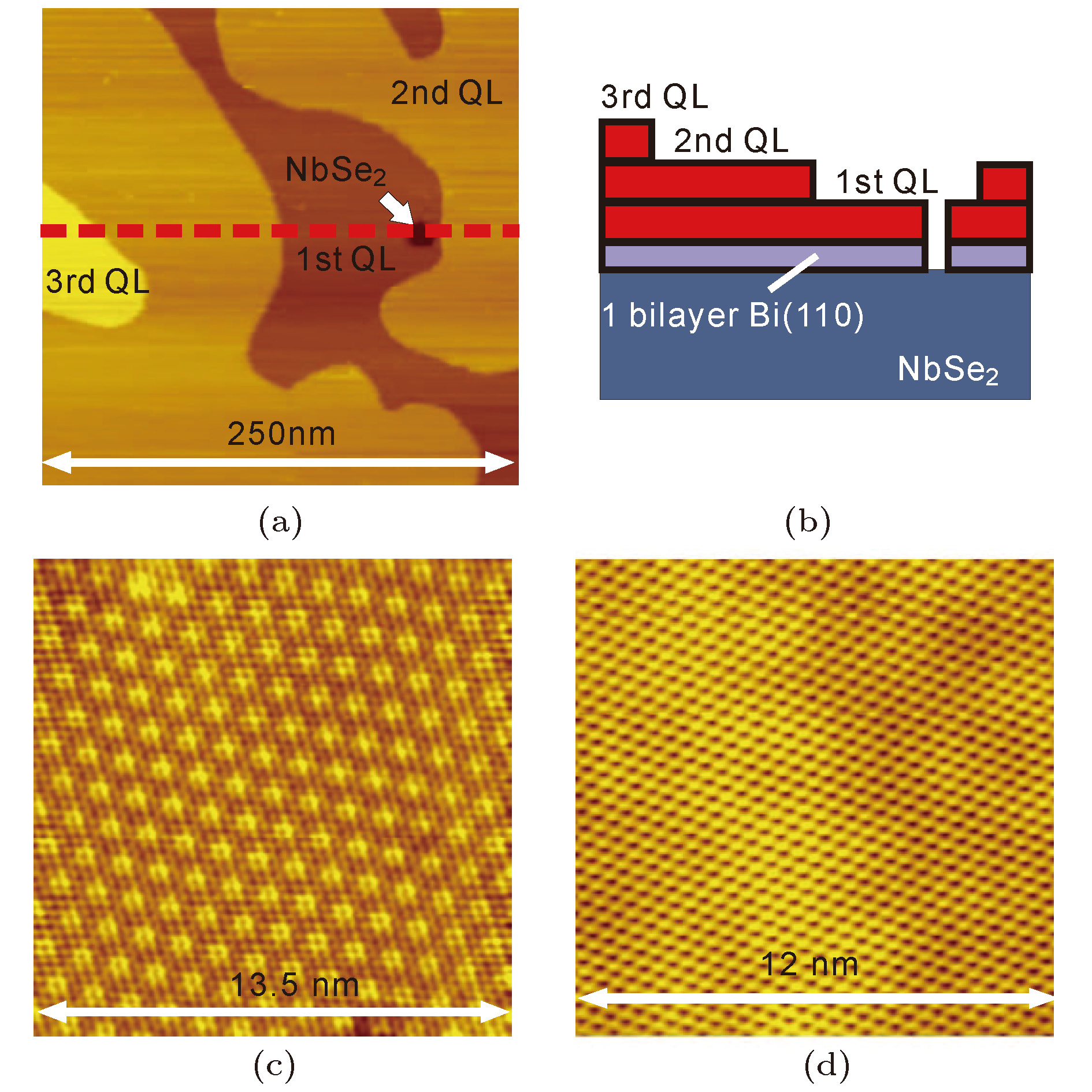
图 1 (a)在NbSe₂衬底上生长的Bi₂Se₃薄膜的形貌; (b)Bi₂Se₃/NbSe₂异质结示意图; (c)NbSe₂衬底表面的原子分辨STM图; (d) Bi₂Se₃薄膜表面的原子分辨STM图^[30]

Figure 1. (a) Morphology of Bi₂Se₃ thin films grown on NbSe₂ substrate; (b) schematic diagram of the Bi₂Se₃/NbSe₂ heterostructure; (c) atomically resolved STM image of the NbSe₂ substrate; (d) atomically resolved STM image of the Bi₂Se₃ film^[30].

DownLoad: Full-Size Img PowerPoint

图 2 在Bi₂Se₃/NbSe₂上探测的超导能隙^[30]　(a) 4.2 K和 (b) 0.4 K温度下3 QL厚的Bi₂Se₃薄膜的dI/dV谱; (c) 4.2 K和 (d) 0.4 K温度下6 QL厚的Bi₂Se₃薄膜的dI/dV谱

Figure 2. Superconducting energy gap detected in Bi₂Se₃ thin films grown on NbSe₂ substrate^[30]: dI/dV spectra measured on 3 QL Bi₂Se₃ films at (a) 4.2 K and (b) 0.4 K; dI/dV spectra measured on 6 QL Bi₂Se₃ films at (c) 4.2 K and (d) 0.4 K.

DownLoad: Full-Size Img PowerPoint

图 3 厚度为　(a) 3 QL, (b) 6 QL, (c) 9 QL, (d) 12 QL 的Bi₂Se₃/NbSe₂的能带结构^[30]

Figure 3. Band structure of (a) 3 QL, (b) 6 QL, (c) 9 QL, (d) 12 QL Bi₂Se₃ thin films grown on NbSe₂ substrate^[30].

DownLoad: Full-Size Img PowerPoint

图 4 (a)在NbSe₂衬底上生长的Bi₂Te₃薄膜的形貌; (b) 2 QL, (c) 3 QL, (d) 5 QL Bi₂Te₃/NbSe₂在4.2 K温度下测得的dI/dV谱^[31]

Figure 4. (a) Morphology of Bi₂Te₃ thin films grown on NbSe₂ substrate; dI/dV spectra measured at 4.2 K on (b) 2 QL, (c) 3 QL, (d) 5 QL Bi₂Te₃/NbSe₂^[31].

DownLoad: Full-Size Img PowerPoint

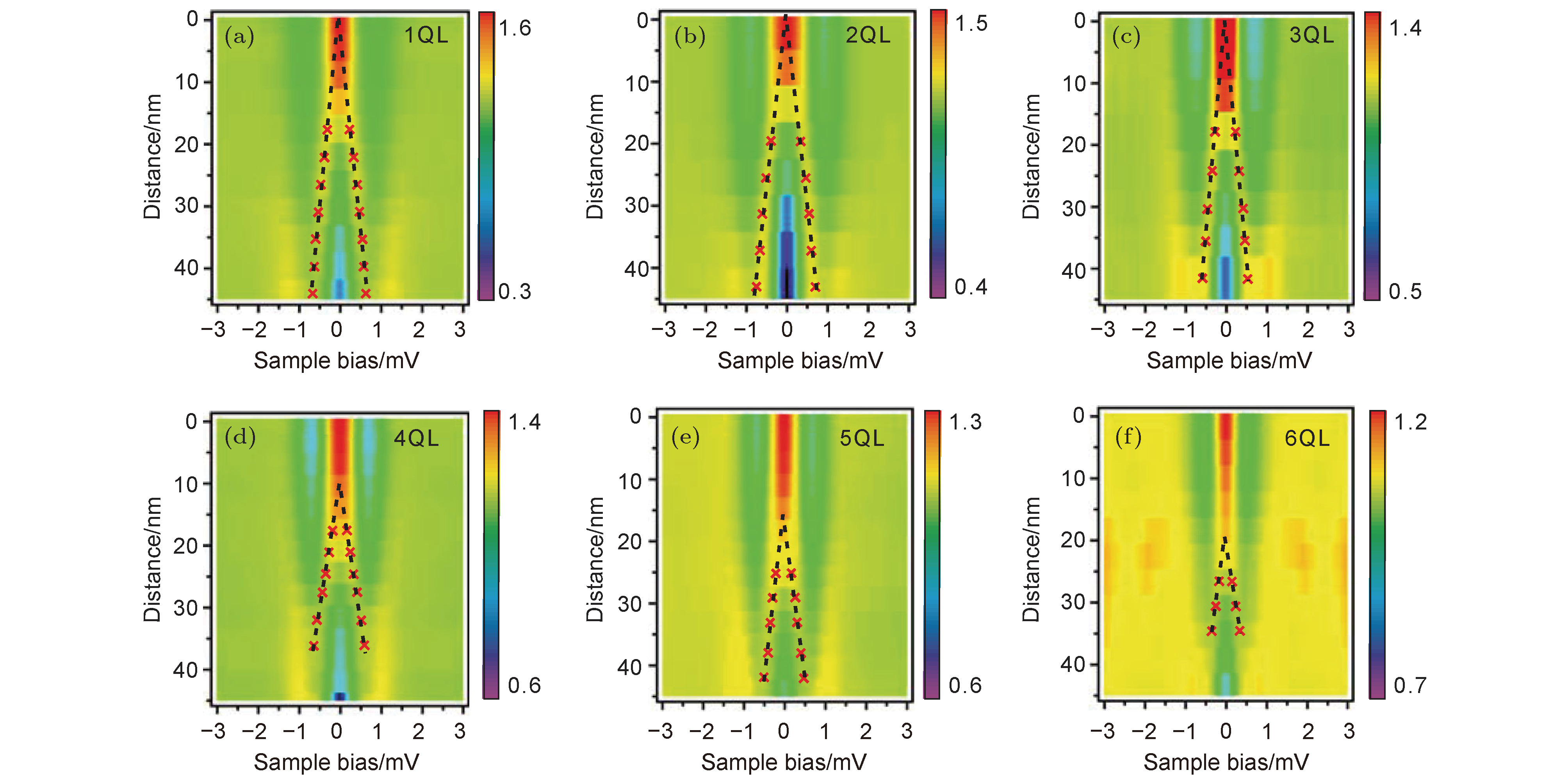
图 5 在Bi₂Te₃/NbSe₂上探测的超导能隙^[31]　(a)各种厚度的Bi₂Te₃薄膜上测得的超导能隙; (b)在NbSe₂衬底, 2 QL以及3 QL Bi₂Te₃/NbSe₂上测得的超导能隙; (c)超导能隙随厚度的变化, 插图为3 QL Bi₂Se₃/NbSe₂的超导能隙. 这些dI/dV谱都是在0.4 K温度下测量的

Figure 5. Superconducting energy gap observed on Bi₂Te₃/NbSe₂^[31]: (a) A series of dI/dV spectra taken on different thicknesses of Bi₂Te₃ thin films at 0.4 K; (b) dI/dV spectra taken on pristine NbSe₂, 2 QL, and 3 QL Bi₂Te₃/NbSe₂; (c) thickness dependence of the superconducting energy gap; Inset is the dI/dV spectra measured at 0.4 K on 3 QL Bi₂Se₃/NbSe₂.

DownLoad: Full-Size Img PowerPoint

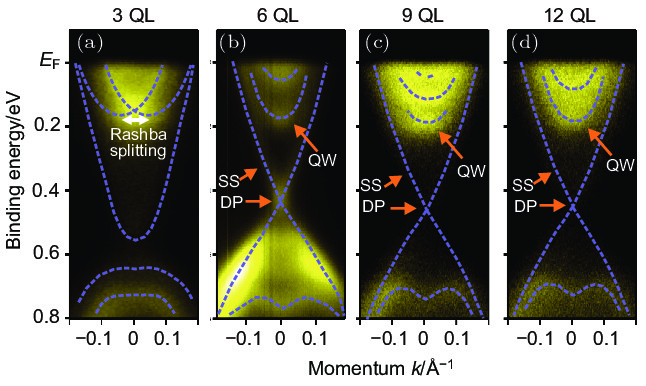
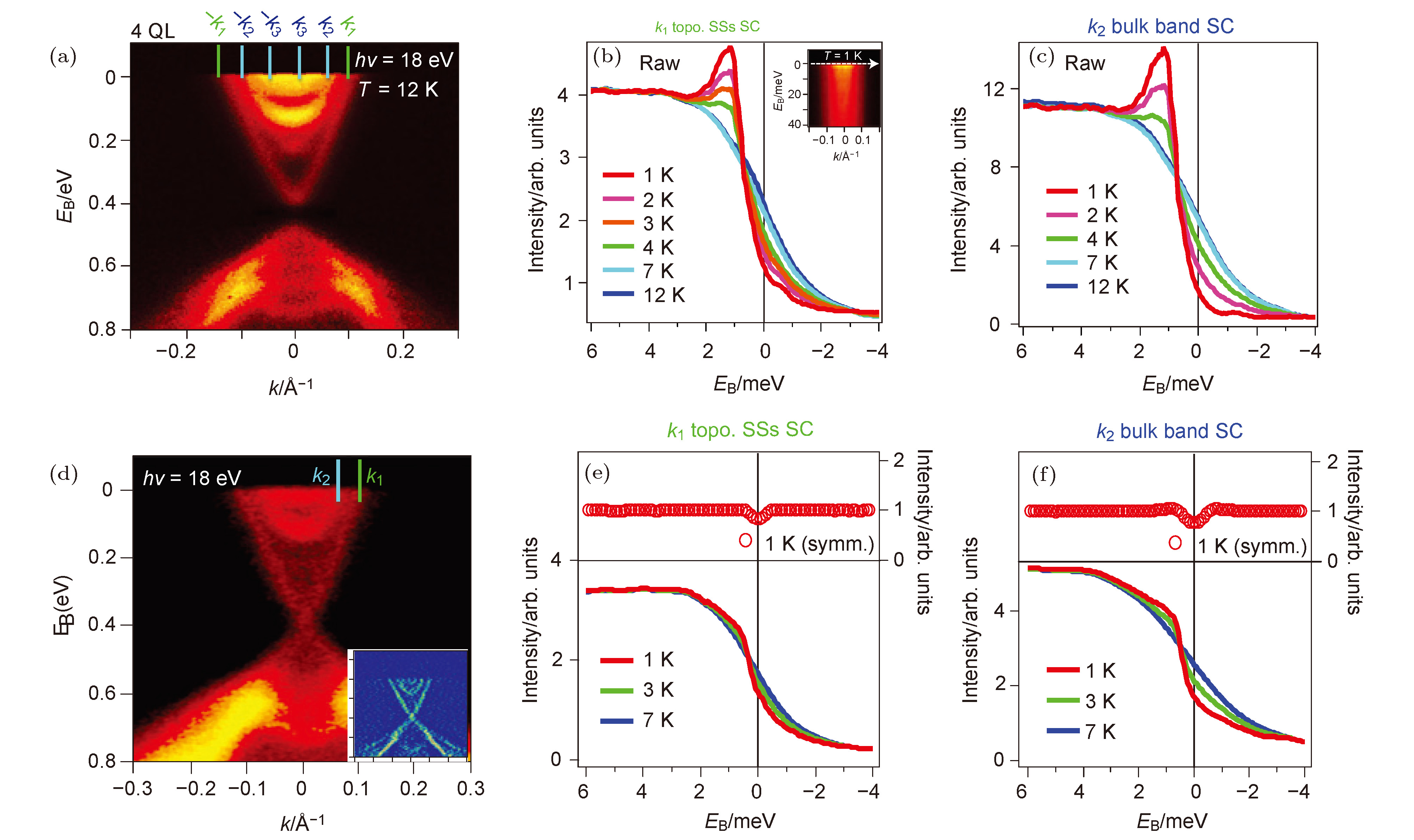
图 6 (a) 12 K时测得的4 QL Bi₂Se₃/NbSe₂的能带结构, 入射光子能量为18 eV; 4 QL 厚的Bi₂Se₃/NbSe₂在 (b) k₁和 (c) k₂处的ARPES谱随温度的变化关系; (d) 12 K时测得的7 QL Bi₂Se₃/NbSe₂的能带结构, 入射光子能量为18 eV; 7 QL 厚的Bi₂Se₃/NbSe₂在 (e) k₁和(f) k₂处的ARPES谱随温度的变化关系^[51]

Figure 6. (a) Band structure of a 4 QL Bi₂Se₃/NbSe₂ measured at 12 K using an incident photon energy of 18 eV; Temperature dependence of ARPES spectra at (b) k₁ and (c) k₂ indicated in Fig. (a); (d) Band structure of a 7 QL Bi₂Se₃/NbSe₂ measured at 12 K using an incident photon energy of 18 eV; Temperature dependence of ARPES spectra at (e) k₁ and (f) k₂ indicated in Fig. (d)^[51].

DownLoad: Full-Size Img PowerPoint

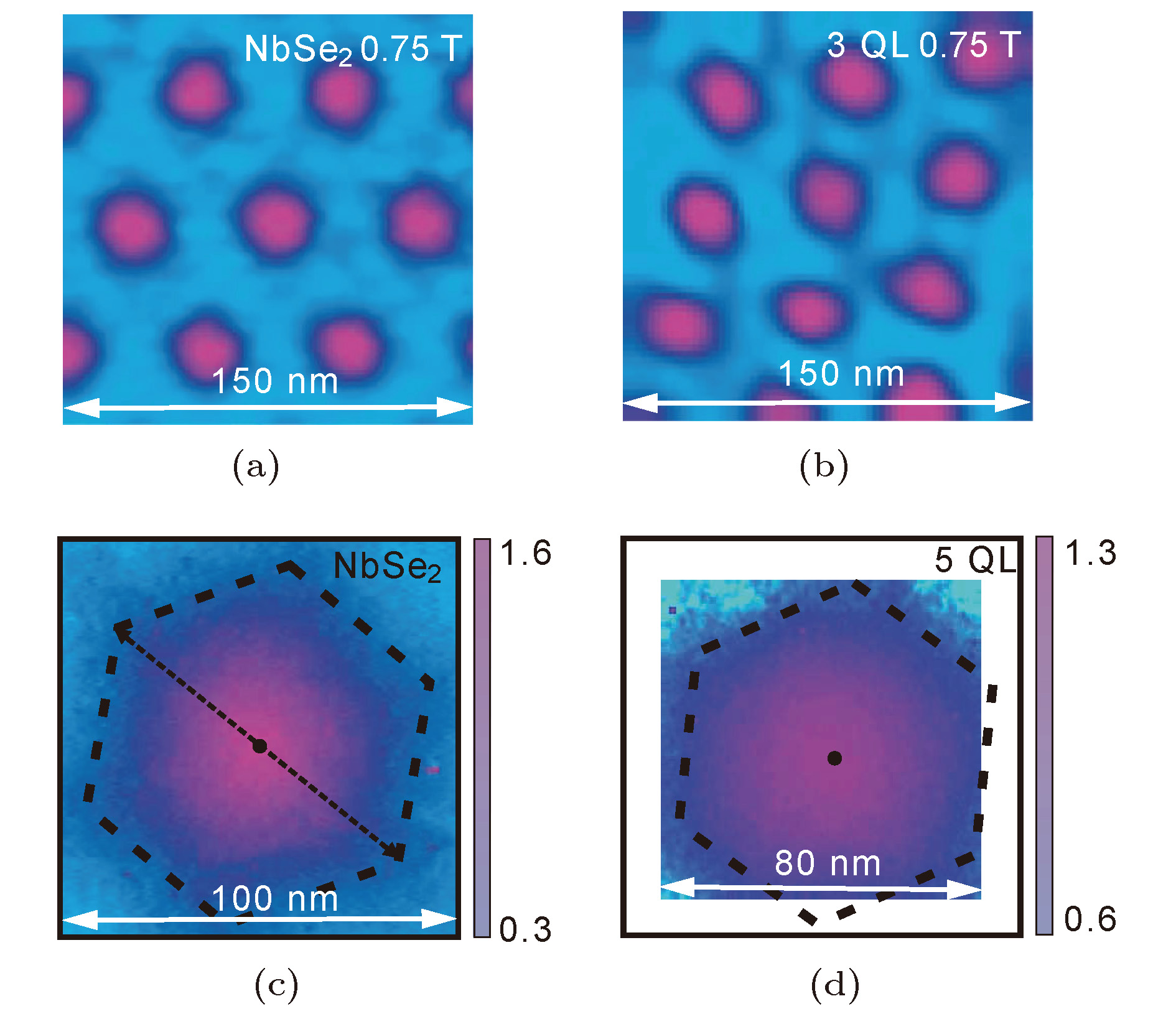
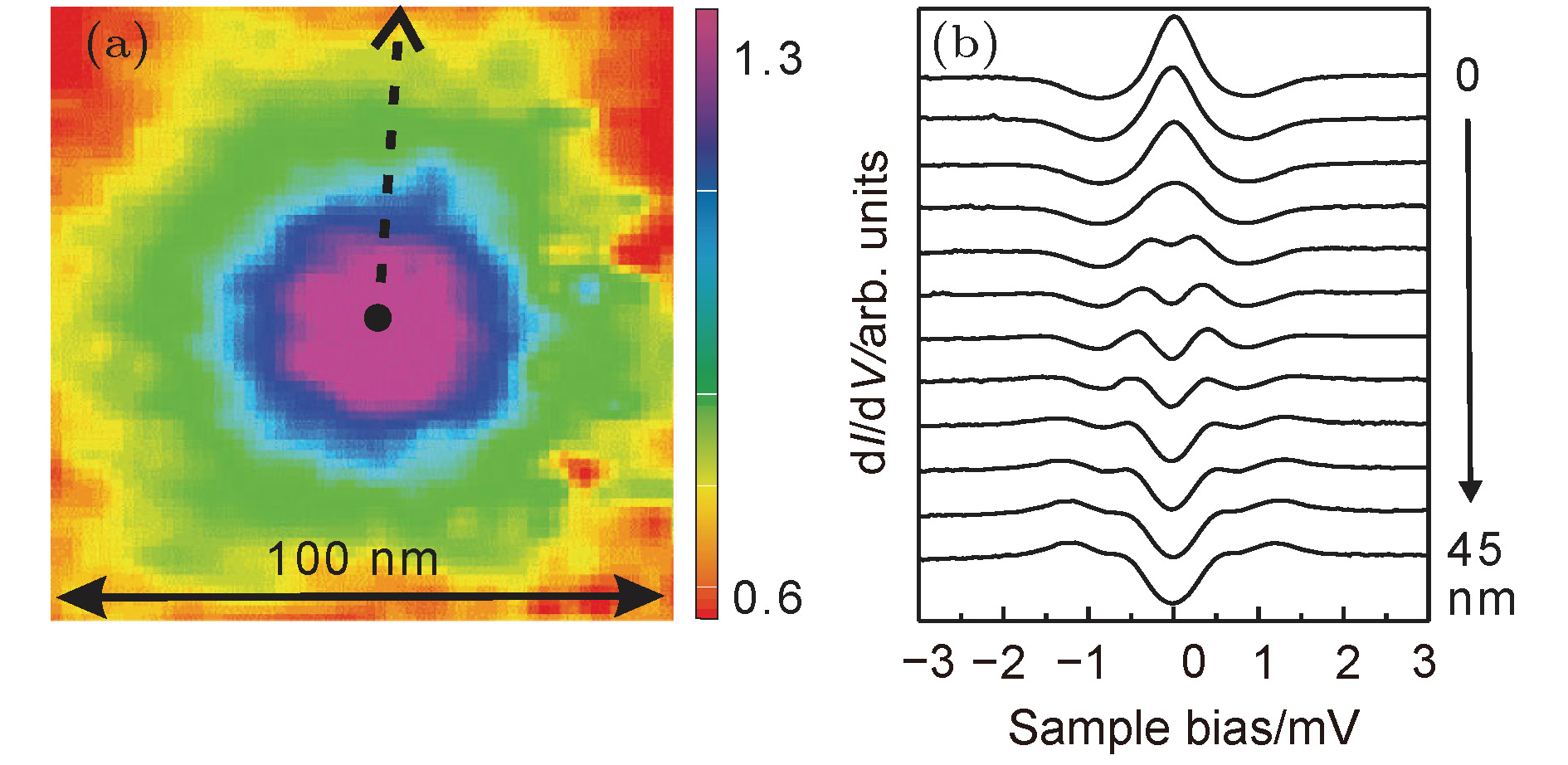
图 7 在0.4 K和0.75 T下在 (a) NbSe₂和 (b) 3 QL Bi₂Te₃/NbSe₂上的零偏压电导的映射图; 在 (c) NbSe₂和 (d) 5 QL Bi₂Te₃/NbSe₂上单个涡旋的零偏压电导的映射图^[31]

Figure 7. Large-scale zero-bias dI/dV maps measured at 0.4 K and 0.75 T on (a) NbSe₂ and (b) 3 QL Bi₂Te₃/NbSe₂; Zero-bias dI/dV maps for a single vortex measured at 0.4 K and 0.1 T on (c) NbSe₂ and (d) 5 QL Bi₂Te₃/NbSe₂^[31].

DownLoad: Full-Size Img PowerPoint

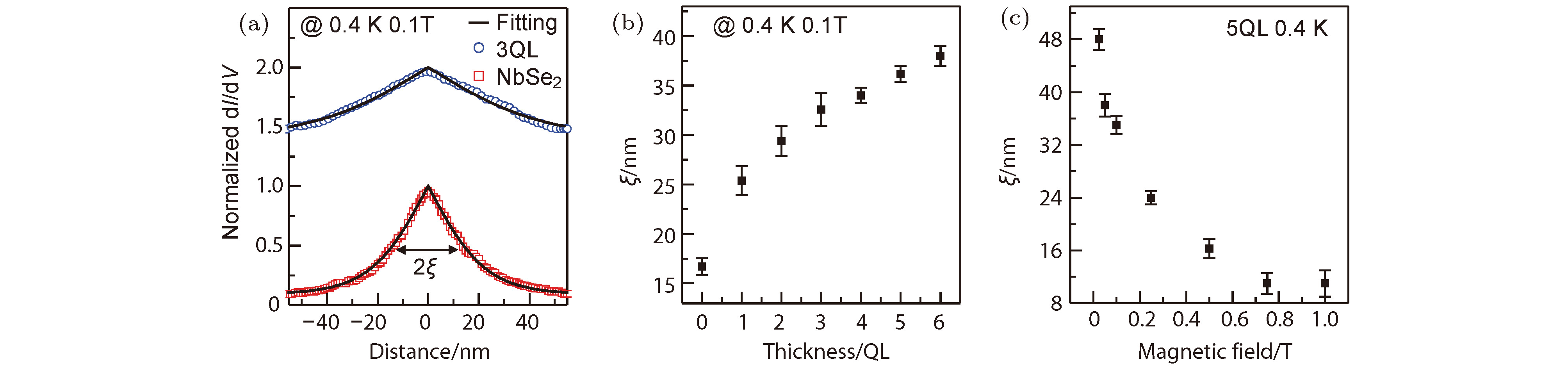
图 8 (a)在0.4 K和0.1 T下在NbSe₂和3 QL Bi₂Te₃/NbSe₂上得到的穿过涡旋中心的零偏压电导轮廓图; (b) Bi₂Te₃/NbSe₂的超导相干长度与薄膜厚度的依赖关系; (c) 5 QL Bi₂Te₃/NbSe₂的超导相干长度与磁场强度的依赖关系^[31]

Figure 8. (a) Normalized ZBC profiles crossing through the centers of vortices at 0.4 K and 0.1 T on NbSe₂ and 3 QL Bi₂Te₃/NbSe₂; (b) thickness dependence of the coherence length; (c) the coherence length as a function of the magnetic field measured on 5 QL Bi₂Te₃/NbSe₂^[31].

DownLoad: Full-Size Img PowerPoint

图 9 (a) 5 QL Bi₂Te₃/NbSe₂, (b) NbSe₂, (c) 2 QL Bi₂Te₃/NbSe₂单个涡旋中心处的dI/dV谱随磁场强度的变化关系^[32]

Figure 9. Magnetic field-dependent dI/dV spectra taken at a vortex center of (a) 5 QL Bi₂Te₃/NbSe₂, (b) pristine NbSe₂, and (c) 2 QL Bi₂Te₃/NbSe₂^[32].

DownLoad: Full-Size Img PowerPoint

图 10 (a)在0.4 K和0.1 T下在5 QL Bi₂Te₃/NbSe₂上单个涡旋的零偏压电导映射图; (b)沿着图(a)中虚线方向做的一系列随空间演化的dI/dV谱^[32]

Figure 10. (a) A vortex mapped by zero bias dI/dV on 5 QL Bi₂Te₃/NbSe₂ at 0.1 T and 0.4 K; (b) spatially resolved dI/dV spectra taken along the dashed line in Fig. (a)^[32].

DownLoad: Full-Size Img PowerPoint

图 11 (a) 1 QL, (b) 2 QL, (c) 3 QL, (d) 4 QL, (e) 5 QL, (f) 6 QL Bi₂Te₃/NbSe₂在0.10 T外加磁场下测得的涡旋中束缚态随空间演化的dI/dV谱强度图^[32]

Figure 11. Spatially resolved bound states within a vortex at 0.10 T in (a) 1 QL, (b) 2 QL, (c) 3 QL, (d) 4 QL, (e) 5 QL, (f) 6 QL Bi₂Te₃/NbSe₂ heterostructures^[32].

DownLoad: Full-Size Img PowerPoint

图 12 (a)在0.10 T外加磁场下5 QL Bi₂Te₃/NbSe₂的单个涡旋中心处束缚态随空间演化的dI/dV谱强度图; (b)在0.18 T外加磁场下5 QL Bi₂Te₃/NbSe₂的单个涡旋中心处束缚态随空间演化的dI/dV谱强度图, 束缚态从一开始就发生劈裂, 这与图(a)形成鲜明的对比^[32]

Figure 12. (a) Spatially resolved bound states within a vortex at 0.10 T in the 5 QL Bi₂Te₃/NbSe₂ heterostructures; (b) spatially resolved bound states within a vortex at 0.18 T in the 5 QL Bi₂Te₃/NbSe₂ heterostructures. The peak-splitting start point is zero, in sharp contrast to that in Fig. (a)^[32].

DownLoad: Full-Size Img PowerPoint

图 13 (a)拓扑超导体5 QL Bi₂Te₃/NbSe₂在0.1 T外加磁场下磁通涡旋的零偏压dI/dV映射图; (b)在磁通涡旋中心用自旋极化的针尖测得的dI/dV谱; (c)在离磁通涡旋中心10 nm远的地方用自旋极化的针尖测得的dI/dV谱^[33]

Figure 13. (a) Zero bias dI/dV mapping of a vortex at 0.1 T on the topological superconductor 5 QL Bi₂Te₃/NbSe₂. (b) dI/dV at the vortex center measured with a fully spin polarized tip. (c) dI/dV at 10 nm away from the center measured with a fully spin polarized tip^[33].

DownLoad: Full-Size Img PowerPoint

图 14 用自旋极化的针尖在磁通涡旋中心测得的dI/dV谱^[33]　(a) 3 QL Bi₂Te₃/NbSe₂, B = 0.1 T; (b) NbSe₂, B = 0.1 T; (c) 5 QL Bi₂Te₃/NbSe₂, B = 0.22 T

Figure 14. dI/dV curves at the center of a vortex core measured with a fully spin polarized tip^[33]: (a) 3 QL Bi₂Te₃/NbSe₂, B = 0.1 T; (b) Bare NbSe₂, B = 0.1 T; (c) 5 QL Bi₂Te₃/NbSe₂, B = 0.22 T.

DownLoad: Full-Size Img PowerPoint

map

[1]	Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057 Google Scholar
[2]	Majorana E 1937 Nuovo Cimento 14 171 Google Scholar
[3]	Moore G, Read N 1991 Nucl. Phys. B 360 362 Google Scholar
[4]	Kitaev A 2003 Ann. Phys. 303 2 Google Scholar
[5]	Nayak C, Simon S H, Stern A, Freedman M, Das Sarma S 2008 Rev. Mod. Phys. 80 1083 Google Scholar
[6]	Wilczek F 2009 Nat. Phys. 5 614 Google Scholar
[7]	Alicea J 2012 Rep. Prog. Phys. 75 076501 Google Scholar
[8]	Beenakker C W J 2013 Annu. Rev. Condens. Mattter Phys. 4 113 Google Scholar
[9]	Leijnse M, Flensberg K 2012 Semicond. Sci. Technol. 27 124003 Google Scholar
[10]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[11]	Fu L, Kane C L 2008 Phys. Rev. Lett. 100 096407 Google Scholar
[12]	Ando Y 2013 J. Phys. Soc. Jpn. 82 102001 Google Scholar
[13]	Yu R, Zhang W, Zhang H J, Zhang S C, Dai X, Fang Z 2010 Science 329 61 Google Scholar
[14]	Chang C Z, Zhang J S, Feng X, Shen J, Zhang Z C, Guo M H, Li K, Ou Y B, Wei P, Wang L L, Ji Z Q, Feng Y, Ji S H, Chen X, Jia J F, Dai X, Fang Z, Zhang S C, He K, Wang Y Y, Lu L, Ma X C, Xue Q K 2013 Science 340 167 Google Scholar
[15]	Schnyder A P, Ryu S, Furusaki A, Ludwig A W W 2008 Phys. Rev. B 78 195125 Google Scholar
[16]	Linder J, Tanaka Y, Yokoyama T, Sudbo A, Nagaosa N 2010 Phys. Rev. Lett. 104 067001 Google Scholar
[17]	Hor Y S, Williams A J, Checkelsky J G, Roushan P, Seo J, Xu Q, Zandbergen H W, Yazdani A, Ong N P, Cava R J 2010 Phys. Rev. Lett. 104 057001 Google Scholar
[18]	Kriener M, Segawa K, Ren Z, Sasaki S, Ando Y 2011 Phys. Rev. Lett. 106 127004 Google Scholar
[19]	Sasaki S, Kriener M, Segawa K., Yada K, Tanaka Y, Sato M, Ando Y 2011 Phys. Rev. Lett. 107 217001 Google Scholar
[20]	Levy N, Zhang T, Ha J, Sharifi F, Alec Talin A, Kuk Y, Stroscio J A 2013 Phys. Rev. Lett. 110 117001 Google Scholar
[21]	Liu Z H, Yao X, Shao J F, Zuo M, Po L, Tan S, Zhang C J, Zhang Y H 2015 J. Am. Chem. Soc. 137 10512 Google Scholar
[22]	Maurya S V K, Neha P, Srivastava P, Patnaik S 2015 Phys. Rev. B 92 020506 Google Scholar
[23]	Lawson B J, Corbae P, Li G, Yu F, Asaba T, Tinsman C, Qiu Y, Medvedeva J E, Hor Y S, Li L 2016 Phys. Rev. B 94 041114 Google Scholar
[24]	Smylie M P, Claus H, Welp U, Kwok W K, Qiu Y, Hor Y S, Snezhko A 2016 Phys. Rev. B 94 180510 Google Scholar
[25]	Yonezawa S, Tajiri K, Nakata S, Nagai Y, Wang Z, Segawa K, Ando Y, Maeno Y 2017 Nat. Phys. 13 123 Google Scholar
[26]	Zhang J L, Zhang S J, Weng H M, Zhang W, Yang L X, Liu Q Q, Feng S M, Wang X C, Yu R C, Cao L Z, Wang L, Yang W G, Liu H Z, Zhao W Y, Zhang S C, Dai X, Fang Z, Jin C Q 2011 Proc. Natl. Acad. Sci. U.S.A. 108 24 Google Scholar
[27]	Zhang C, Sun L, Chen Z, Zhou X, Wu Q, Yi W, Guo J, Dong X, Zhao Z 2011 Phys. Rev. B 83 140504 Google Scholar
[28]	Kirshenbaum K, Syers P S, Hope A P, Butch N P, Jeffries J R, Weir S T, Hamlin J J, Maple M B, Vohra Y K, Paglione J 2013 Phys. Rev. Lett. 111 087001 Google Scholar
[29]	Zhu J, Zhang J L, Kong P P, Zhang S J, Yu X H, Zhu J L, Liu Q Q, Li X, Yu R C, Ahuja R, Yang W G, Shen G Y, Mao H K, Weng H M, Dai X, Fang Z, Zhao Y S, Jin C Q 2013 Sci. Rep. 3 2016 Google Scholar
[30]	Wang M X, Liu C H, Xu J P, Yang F, Miao L, Yao M Y, Gao C L, Shen C, Ma X C, Chen X, Xu Z A, Liu Y, Zhang S C, Qian D, Jia J F, Xue Q K 2012 Science 336 52 Google Scholar
[31]	Xu J P, Liu C H, Wang M X, Ge J F, Liu Z L, Yang X J, Chen Y, Liu Y, Xu Z A, Gao C L, Qian D, Zhang F C, Jia J F 2014 Phys. Rev. Lett. 112 217001 Google Scholar
[32]	Xu J P, Wang M X, Liu Z L, Ge J F, Yang X J, Liu C H, Xu Z A, Guan D D, Gao C L, Qian D, Liu Y, Wang Q H, Zhang F C, Xue Q K, Jia J F 2015 Phys. Rev. Lett. 114 017001 Google Scholar
[33]	Sun H H, Zhang K W, Hu L H, Li C, Wang G Y, Ma H Y, Xu Z A, Gao C L, Guan D D, Li Y Y, Liu C H, Qian D, Zhou Y, Fu L, Li S C, Zhang F C, Jia J F 2016 Phys. Rev. Lett. 116 257003 Google Scholar
[34]	Qu F, Yang F, Shen J, Ding Y, Chen J, Ji Z, Liu G, Fan J, Jing X, Yang C, Lu L 2012 Sci. Rep. 2 339 Google Scholar
[35]	Hart S, Ren H, Wagner T, Leubner P, Mühlbauer M, Brüne C, Buhmann H, Molenkamp L W, Yacoby A 2014 Nat. Phys. 10 638 Google Scholar
[36]	Knez I, Du R R, Sullivan G 2012 Phys. Rev. Lett. 109 186603 Google Scholar
[37]	Pribiag V S, Beukman A J A, Qu F, Cassidy M C, Charpentier C, Wegscheider W, Kouwenhoven L P 2015 Nat. Nanotechnol. 10 593 Google Scholar
[38]	He Q L, Pan L, Stern A L, Burks E C, Che X, Yin G, Wang J, Lian B, Zhou Q, Choi E S, Murata K, Kou X, Chen Z, Nie T, Shao Q, Fan Y, Zhang S C, Liu K, Xia J, Wang K L 2017 Science 357 294 Google Scholar
[39]	Mourik V, Zuo K, Frolov S M, Plissard S R, Bakkers E P A M, Kouwenhoven L P 2012 Science 336 1003 Google Scholar
[40]	Deng M T, Yu C L, Huang G Y, Larsson M, Caroff P, Xu H Q 2012 Nano Lett. 12 6414 Google Scholar
[41]	Nadj-Perge S, Drozdov I K, Li J, Chen H, Jeon S, Seo J, MacDonald A H, Bernevig B A, Yazdani A 2014 Science 346 602 Google Scholar
[42]	Koma A 1999 J. Cryst. Growth 201 236
[43]	Zhang H J, Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2009 Nat. Phys. 5 438 Google Scholar
[44]	Meerschaut A, Deudon C 2001 Mater. Res. Bull. 36 1721 Google Scholar
[45]	Zhang Y, He K, Chang C Z, Song C L, Wang L L, Chen X, Jia J F, Fang Z, Dai X, Shan W Y, Shen S Q, Niu Q, Qi X L, Zhang S C, Ma X C, Xue Q K 2010 Nat. Phys. 6 584 Google Scholar
[46]	Li Y Y, Wang G, Zhu X G, Liu M H, Ye C, Chen X, Wang Y Y, He K, Wang L L, Ma X C, Zhang H J, Dai X, Fang Z, Xie X C, Liu Y, Qi X L, Jia J F, Zhang S C, Xue Q K 2010 Adv. Mater. 22 4002 Google Scholar
[47]	Park K, Heremans J J, Scarola V W, Minic D 2010 Phys. Rev. Lett. 105 186801 Google Scholar
[48]	Liu Y, Bian G, Miller T, Bissen M, Chiang T C 2012 Phys. Rev. B 85 195442 Google Scholar
[49]	Black-Schaffer A M, Balatsky A V 2013 Phys. Rev. B 87 220506 Google Scholar
[50]	Tkachov G 2013 Phys. Rev. B 87 245422 Google Scholar
[51]	Xu S Y, Alidoust N, Belopolski I, Richardella A, Liu C, Neupane M, Bian G, Huang S H, Sankar R, Fang C, Dellabetta B, Dai W Q, Li Q, Gilbert M J, Chou F C, Samarth N, Hasan M Z 2014 Nat. Phys. 10 943 Google Scholar
[52]	Hess H F, Robinson R B, Dynes R C, Valles J M, Waszczak J V 1989 Phys. Rev. Lett. 62 214 Google Scholar
[53]	Eskildsen M R, Kugler M, Tanaka S, Jun J, Kazakov S M, Karpinski J, Fischer O 2002 Phys. Rev. Lett. 89 187003 Google Scholar
[54]	Sonier J E, Kiefl R F, Brewer J H, Chakhalian J, Dunsiger S R, MacFarlane W A, Miller R I, Wong A, Luke G M, Brill J W 1997 Phys. Rev. Lett. 79 1742 Google Scholar
[55]	Miller R I, Kiefl R F, Brewer J H, Chakhalian J, Dunsiger S, Morris G D, Sonier J E, MacFarlane W A 2000 Phys. Rev. Lett. 85 1540 Google Scholar
[56]	Chiu C K, Gilbert M J, Hughes T L 2011 Phys. Rev. B 84 144507 Google Scholar
[57]	Gygi F, Schluter M 1991 Phys. Rev. B 43 7609 Google Scholar
[58]	Kawakami T, Hu X 2015 Phys. Rev. Lett. 115 177001 Google Scholar
[59]	He J J, Ng T K, Lee P A, Law K T 2014 Phys. Rev. Lett. 112 037001 Google Scholar
[60]	Wiesendanger R 2009 Rev. Mod. Phys. 81 1495 Google Scholar
[61]	Hu L H, Li C, Xu D H, Zhou Y, Zhang F C 2016 Phys. Rev. B 94 224501 Google Scholar
[62]	Elliott S R, Franz M 2015 Rev. Mod. Phys. 87 137 Google Scholar
[63]	Kitaev A Y 2001 Phys. Usp. 44 131 Google Scholar
[64]	Law K T, Lee P A, Ng T K 2009 Phys. Rev. Lett. 103 237001 Google Scholar
[65]	Wimmer M, Akhmerov A R, Dahlhaus J P, Beenakker C W J 2011 New J. Phys. 13 053016 Google Scholar
[66]	Nilsson J, Akhmerov A R, Beenakker C W J 2008 Phys. Rev. Lett. 101 120403 Google Scholar
[67]	Fu L 2010 Phys. Rev. Lett. 104 056402 Google Scholar
[68]	Burnell F J, Shnirman A, Oreg Y 2013 Phys. Rev. B 88 224507 Google Scholar
[69]	Zhang P, Yaji K, Hashimoto T, Ota Y, Kondo T, Okazaki K, Wang Z, Wen J, Gu G D, Ding H, Shin S 2018 Science 360 182 Google Scholar
[70]	Wang D, Kong L, Fan P, Chen H, Zhu S, Liu W, Cao L, Sun Y, Du S, Schneeloch J, Zhong R, Gu G, Fu L, Ding H, Gao H J 2018 Science 362 333 Google Scholar
[71]	Liu Q, Chen C, Zhang T, Peng R, Yan Y J, Wen C H P, Lou X, Huang Y L, Tian J P, Dong X L, Wang G W, Bao W C, Wang Q H, Yin Z P, Zhao Z X, Feng D L 2018 Phys. Rev. X 8 041056 Google Scholar

[1]	Yong Kang-Le, Yan Jia-Wei, Tang Shan-Fa, Zhang Rong-Zhu. Influence of coma and spherical aberration on transmission characteristics of vortex beams in slant atmospheric turbulence. Acta Physica Sinica, 2020, 69(1): 014201. doi: 10.7498/aps.69.20191254
[2]	Jiang Guang-Yu, Sun Chao, Li Qin-Ran. Effect of mesoscale eddies on the vertical spatial characteristics of wind-generated noise in deep ocean. Acta Physica Sinica, 2020, 69(14): 144301. doi: 10.7498/aps.69.20200059
[3]	Chen Guang-Ping. Ground state of a rotating spin-orbit-coupled Bose-Einstein condensate in a harmonic plus quartic potential. Acta Physica Sinica, 2015, 64(3): 030302. doi: 10.7498/aps.64.030302
[4]	Shi Liang-Ma, Zhou Ming-Jian, Zhu Ren-Yi. Evolution of vortex configuration for superconducting ring in the presence of an externally applied field. Acta Physica Sinica, 2014, 63(24): 247501. doi: 10.7498/aps.63.247501
[5]	Liu Chao-Fei, Wan Wen-Juan, Zhang Gan-Yuan. Vortex pattern in spin-orbit coupled spin-1 Bose-Einstein condensate of 23Na. Acta Physica Sinica, 2013, 62(20): 200306. doi: 10.7498/aps.62.200306
[6]	Zhou Yu, Zhou Qing-Chun, Ma Xiao-Dong. Vortex of an anomalous mode in Fermi gas near unitarity limit. Acta Physica Sinica, 2013, 62(14): 140301. doi: 10.7498/aps.62.140301
[7]	Ma Ying, Wang Cang-Long, Wang Wen-Yuan, Yang Yang, Ma Yun-Yun, Meng Hong-Juan, Duan Wen-Shan. The tunneling phenomena of the Fermi superfluid gases in unitarity by manipulating the Fermi-Fermi scattering length. Acta Physica Sinica, 2012, 61(18): 180303. doi: 10.7498/aps.61.180303
[8]	He Li, Qiao Wen-Tao, Zhang Li-Wei, Xu Jing-Ping. Electromagnetic tunneling properties of sandwich structure containing single negative material. Acta Physica Sinica, 2010, 59(11): 7863-7868. doi: 10.7498/aps.59.7863
[9]	Li Gao-Qing, Chen Hai-Jun, Xue Ju-Kui. One-dimensional tunneling dynamics between two-component Bose-Einstein condensates. Acta Physica Sinica, 2010, 59(3): 1449-1455. doi: 10.7498/aps.59.1449
[10]	Fang Yong-Cui, Yang Zhi-An. Chaos tunneling of Bose-Einstein condensates. Acta Physica Sinica, 2008, 57(12): 7438-7446. doi: 10.7498/aps.57.7438
[11]	Jin Hua, Liu Shu, Zhang Zhen-Zhong, Zhang Li-Gong, Zheng Zhu-Hong, Shen De-Zhen. Exciton tunnelling in (CdZnTe,ZnSeTe)/ZnTe complex quantum wells. Acta Physica Sinica, 2008, 57(10): 6627-6630. doi: 10.7498/aps.57.6627
[12]	Wang Guan-Fang, Liu Hong. Irregular spin tunneling for Bose-Einstein condensates in a sweeping magnetic field. Acta Physica Sinica, 2008, 57(2): 667-673. doi: 10.7498/aps.57.667
[13]	Li Qian, Wang Zhi-Guo, Liu Su, Xing Zhong-Wen, Liu Mei. Theoretical study on electric-pulse-induced resistance change in perovskite Pr1－xCaxMnO3 films. Acta Physica Sinica, 2007, 56(3): 1637-1642. doi: 10.7498/aps.56.1637
[14]	Wang Li, Wang Qing-Feng, Wang Xi-Qing, Lü Bai-Da. Transversal optical vortex in the interference field of two off-axis Gaussian beams. Acta Physica Sinica, 2007, 56(1): 201-207. doi: 10.7498/aps.56.201
[15]	Hu Ya-Peng, Zhang Jing-Yi, Zhao Zheng. Further discussions on the Hawking radiation of charged particles via tunneling from the Reissner-Norstrom black hole. Acta Physica Sinica, 2007, 56(2): 683-685. doi: 10.7498/aps.56.683
[16]	Li Yong-Qing, Li Xi-Guo, Liu Zi-Yu, Luo Pei-Yan, Zhang Peng-Ming. New vortex solutions of Jackiw-Pi model. Acta Physica Sinica, 2007, 56(11): 6178-6182. doi: 10.7498/aps.56.6178
[17]	Wang Wen-Gang, Liu Zheng-You, Zhao De-Gang, Ke Man-Zhu. Resonant tunneling of acoustic waves in 1D phononic crystal. Acta Physica Sinica, 2006, 55(9): 4744-4747. doi: 10.7498/aps.55.4744
[18]	Wu Zhuo-Jie, Zhu Ka-Di, Yuan Xiao-Zhong, Zheng Hang. Influence of electron-phonon interaction on single electron tunneling in a quantum dot molecule. Acta Physica Sinica, 2005, 54(7): 3346-3350. doi: 10.7498/aps.54.3346
[19]	Han Yi-Wen. Using quantum tunneling method Hawking radiation of a static black hole horizon with a mass-quadrupole moment is studied. Acta Physica Sinica, 2005, 54(11): 5018-5021. doi: 10.7498/aps.54.5018
[20]	Jin Hua, Zhang Li-Gong, Zheng Zhu-Hong, Kong Xiang-Gui, An Li-Nan, Shen De-Zhen. Exciton tunnelling in ZnCdSe quantum well/CdSe quantum dots. Acta Physica Sinica, 2004, 53(9): 3211-3214. doi: 10.7498/aps.53.3211

Catalog

Vol. 68, Issue 13 - 2019-07-05

Metrics

Abstract views: 14053
PDF Downloads: 728
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板