-
利用数值模拟含时薛定谔方程的方法, 研究了氢原子在强激光场作用下产生的阈下高次谐波辐射. 在波长为608 nm激光作用下, 氢原子可以吸收5个光子, 由基态$\left|1{\mathrm{s}}\right\rangle$共振跃迁至激发态$\left|2{\mathrm{p}}\right\rangle$态; 氢原子也可以吸收更多光子发生电离, 某些连续态$\left|{\mathrm{c}}\right\rangle$在激光缀饰下能量和$\left|2{\mathrm{p}}\right\rangle$态能量相当. 随后发生的$\left|2{\mathrm{p}}\right\rangle \leftrightarrow \left|1{\mathrm{s}}\right\rangle$复合, 或$\left|{\mathrm{c}}\right\rangle \leftrightarrow \left|1{\mathrm{s}}\right\rangle$复合, 可辐射出能量相同的光子. 这两个复合路径相互干涉, 在第5次谐波中形成典型的法诺线形. 进一步研究发现, 该法诺线形依赖于激光强度. 本研究表明, 即便是在单电子体系中, 法诺干涉也可以存在, 并且可以通过控制激光参数改变法诺线形.We numerically solved the time-dependent Schrödinger equation (TDSE) for a hydrogen atom interacting with intense near-infrared laser fields to investigate the mechanism of below-threshold high-harmonic generation (HHG). The primary focus was on understanding the spectral features, particularly resonant structures, arising in the fifth harmonic region under specific driving conditions. Our simulations utilized a laser wavelength of 608 nm. At this wavelength, hydrogen atoms can resonantly absorb five photons, promoting electrons from the ground stateWe numerically solved the time-dependent Schrödinger equation (TDSE) for a hydrogen atom interacting with intense near-infrared laser fields to investigate the mechanism of below-threshold high-harmonic generation (HHG). The primary focus was on understanding the spectral features, particularly resonant structures, arising in the fifth harmonic region under specific driving conditions. Our simulations utilized a laser wavelength of 608 nm. At this wavelength, hydrogen atoms can resonantly absorb five photons, promoting electrons from the ground state $\left|1{\mathrm{s}}\right\rangle$ to the excited state $\left|2{\mathrm{p}}\right\rangle$. Concurrently, the atom can absorb additional photons leading to ionization. Crucially, due to the AC Stark shift induced by the intense laser field (laser dressing), some laser-dressed continuum states $\left|{\mathrm{c}}\right\rangle$ become energetically degenerate with the laser-dressed $\left|2{\mathrm{p}}\right\rangle$ state. High-harmonic radiation at the fifth harmonic frequency can then be emitted via two distinct quantum paths: 1) Bound-bound recombination: Direct recombination from the laser-dressed $\left|2{\mathrm{p}}\right\rangle$ state back to the ground state $\left|1{\mathrm{s}}\right\rangle$. 2) Continuum-bound recombination: recombination from the laser-dressed continuum states $\left|{\mathrm{c}}\right\rangle$ (reached via ionization) back to $\left|1{\mathrm{s}}\right\rangle$. Both pathways emit photons of identical energy corresponding to the fifth harmonic. Our important finding is that there is significant quantum interference between these two recombination channels. This interference is manifested in the spectrum as an asymmetric Fano lineshape of the fifth harmonic intensity profile. Furthermore, we demonstrate that the shape of this Fano resonance exhibits strong and controllable dependence on the intensity of the driving laser field. This study provides clear evidence that Fano quantum interference, typically associated with multi-electron correlations or autoionizing states in complex systems, can emerge in the fundamental single-electron hydrogen atom system under the condition of intense laser field. The interference arises directly from the coherent superposition of the bound-bound and continuum-bound recombination pathways caused by laser-induced degeneracy. Importantly, by adjusting the laser intensity the spectral profile of the Fano resonance can be actively manipulated, providing a novel method for coherently controlling the harmonic emission in simple atomic systems.
-
Keywords:
- hydrogen atom /
- intense laser field /
- below-threshold high-harmonic generation /
- Fano resonance
[1] Fano U 1961 Phys. Rev. 124 1866
Google Scholar
[2] Kobayashi K, Aikawa H, Katsumoto S, Iye Y 2002 Phys. Rev. Lett. 88 256806
Google Scholar
[3] Wang Y, Liao L, Hu T, Luo S, Wu L, Wang J, Zhang Z, Xie W, Sun L, Kavokin A V, Shen X, Chen Z 2017 Phys. Rev. Lett. 118 063602
Google Scholar
[4] Karmakar S, Kumar D, Varshney R K, Chowdhury D R 2020 Opt. Lett. 45 3386
Google Scholar
[5] Ott C, Aufleger L, Ding T, et al. 2019 Phys. Rev. Lett. 123 163201
Google Scholar
[6] Fasshauer E, Madsen L B 2020 Phys. Rev. A 101 043414
Google Scholar
[7] Wickenhauser M, Burgdörfer J, Krausz F, Drescher M 2005 Phys. Rev. Lett. 94 023002
Google Scholar
[8] Themelis S I, Lambropoulos P, Meyer M 2004 J. Phys. B: At. Mol. Opt. Phys. 37 4281
Google Scholar
[9] Tong X M, Lin C D 2005 Phys. Rev. A 71 033406
Google Scholar
[10] Zhao Z X, Lin C D 2005 Phys. Rev. A 71 060702
Google Scholar
[11] Wang H, Chini M, Chen S, Zhang C H, He F, Cheng Y, Wu Y, Thumm U, Chang Z 2010 Phys. Rev. Lett. 105 143002
Google Scholar
[12] Kaldun A, Ott C, Blättermann A, Laux M, Meyer K, Ding T, Fischer A, Pfeifer T 2014 Phys. Rev. Lett. 112 103001
Google Scholar
[13] Kaldun A, Blättermann A, Stooß V, Donsa S, Wei H, Pazourek R, Nagele S, Ott C, Lin C D, Burgdörfer J, Pfeifer T 2016 Science 354 738
Google Scholar
[14] Peng P, Marceau C, Hervé M, Corkum P B, Naumov A Y, Villeneuve D M 2019 Nat. Commun. 10 5269
Google Scholar
[15] Stooß V, Birk P, Blättermann A, Hartmann M, Borisova G D, Ott C, Pfeifer T 2020 Phys. Rev. Res. 2 032041
Google Scholar
[16] Harkema N, Cariker C, Lindroth E, Argenti L, Sandhu A 2021 Phys. Rev. Lett. 127 023202
Google Scholar
[17] Peng P, Mi Y H, Lytova M, Britton M, Ding X Y, Naumov A Y, Corkum P B, Villeneuve D M 2022 Nat. Photonics 16 4551
Google Scholar
[18] Serov V V, Kheifets A S 2024 Phys. Rev. A 110 043107
Google Scholar
[19] Han M, Liang H, Ji J B, Sum L C, Ueda K, Rost J M, Wörner H J 2025 Ultrafast Science 5 0091
Google Scholar
[20] Lewenstein M, Balcou P, Ivanov M Y, L'Huillier A, Corkum P B 1994 Phys. Rev. A 49 2117
Google Scholar
[21] Soifer H, Botheron P, Shafir D, Diner A, Raz O, Bruner B D, Mairesse Y, Pons B, Dudovich N 2010 Phys. Rev. Lett. 105 143904
Google Scholar
[22] Yost D C, Schibli T R, Ye J, Tate J L, Hostetter J, Gaarde M B, Schafer K J 2009 Nat. Phys. 5 815820
Google Scholar
[23] Hostetter J A, Tate J L, Schafer K J, Gaarde M B 2010 Phys. Rev. A 82 023401
Google Scholar
[24] Xiong W H, Geng J W, Tang J Y, Peng L Y, Gong Q 2014 Phys. Rev. Lett. 112 233001
Google Scholar
[25] Xiong W H, Jin J Z, Peng L Y, Gong Q 2017 Phys. Rev. A 96 023418
Google Scholar
[26] Camp S, Schafer K J, Gaarde M B 2015 Phys. Rev. A 92 013404
Google Scholar
[27] Li P C, Sheu Y L, Laughlin C, Chu S I 2015 Nat. Commun. 6 7178
Google Scholar
[28] Chu W C, Travers J C, Russell P S J 2016 New J. Phys. 18 023018
Google Scholar
[29] Beaulieu S, Camp S, Descamps D, Comby A, Wanie V, Petit S, Légaré F, Schafer K J, Gaarde M B, Catoire F, Mairesse Y 2016 Phys. Rev. Lett. 117 203001
Google Scholar
[30] Du L L, Wang G L, Li P C, Zhou X X, Zhao Z X 2018 Phys. Rev. A 97 023404
Google Scholar
[31] Guo Q L, Li P C, Zhou X X, Chu S I 2018 Opt. Commun. 410 262
Google Scholar
[32] Wang B, Zhang Y, Lan P, Zhai C, Li M, Zhu X, Chen J, Lu P, Lin C D 2021 Phys. Rev. A 103 053119
Google Scholar
[33] Park T J, Light J C 1986 J. Chem. Phys. 85 5870
Google Scholar
[34] Burnett K, Reed V C, Cooper J, Knight P L 1992 Phys. Rev. A 45 3347
Google Scholar
[35] Sundaram B, Milonni P W 1990 Phys. Rev. A 41 6571
Google Scholar
[36] Figueira de Morisson Faria C, Dörr M, Sandner W 1998 Phys. Rev. A 58 2990
Google Scholar
[37] Figueira de Morisson Faria C, Rotter I 2002 Phys. Rev. A 66 013402
Google Scholar
[38] Bickel W S, Goodman A S 1966 Phys. Rev. 148 1
Google Scholar
[39] Bo L, Rujiang L, Jiahui F, Qun W, Kuang Z, Wan C, Zhefei W, Ruyu M 2016 Sci. Rep. 6 31884
Google Scholar
[40] Iizawa M, Kosugi S, Koike F, Azuma Y 2021 Phys. Scr. 96 055401
Google Scholar
-
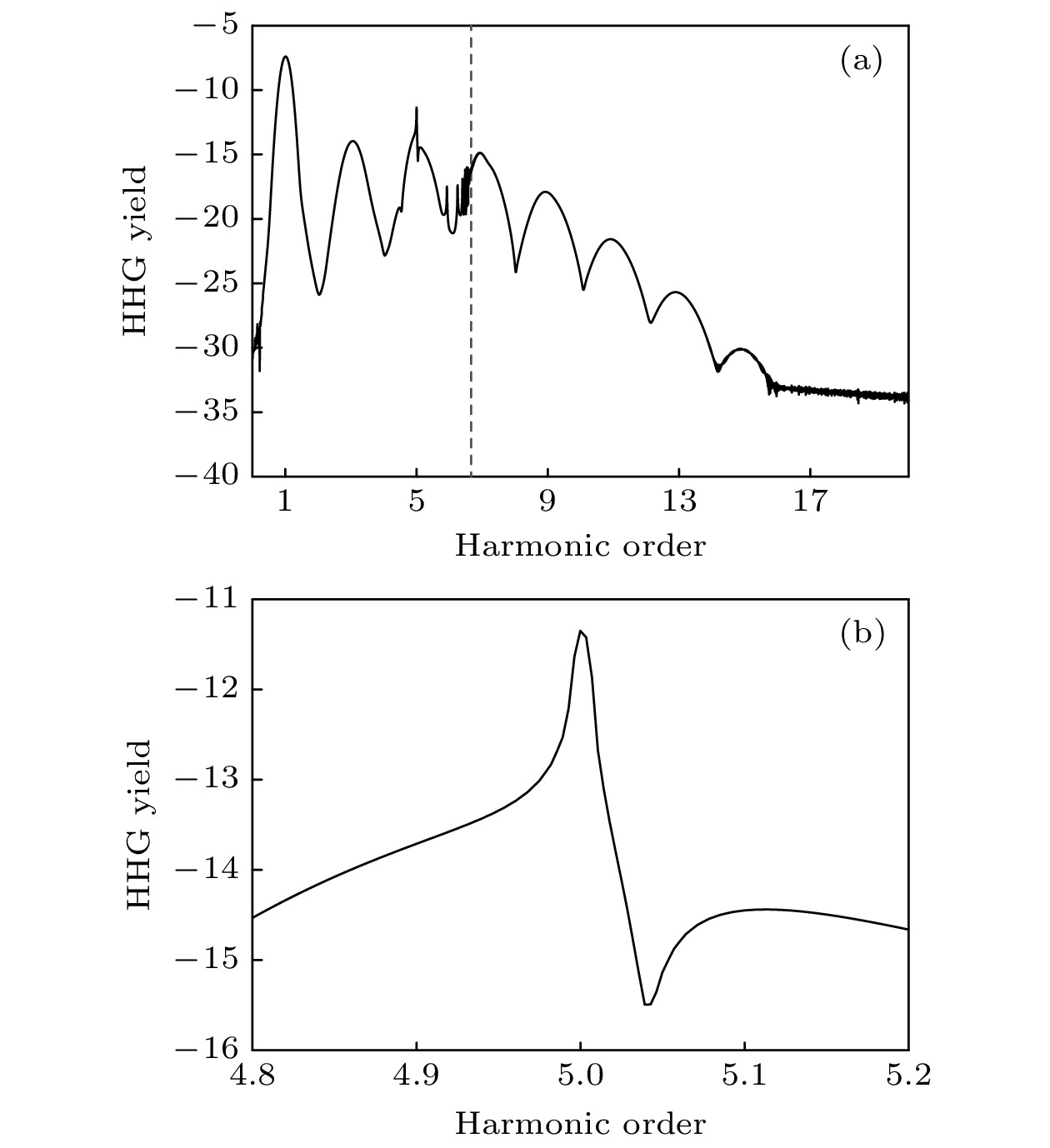
图 1 (a)计算得到的高次谐波谱, 虚线标记了阈上和阈下谐波能量的分界点; (b)图(a)中第5次谐波的局部放大图. 激光波长为608 nm, 强度为5 × 1012 W·cm–2
Fig. 1. (a) Calculated high-harmonic spectrum, the dashed line marks the boundary between above-threshold and below-threshold harmonic energies; (b) partial enlarged view of the fifth harmonic in panel (a). The laser wavelength is 608 nm with an intensity of 5 × 1012 W·cm–2.
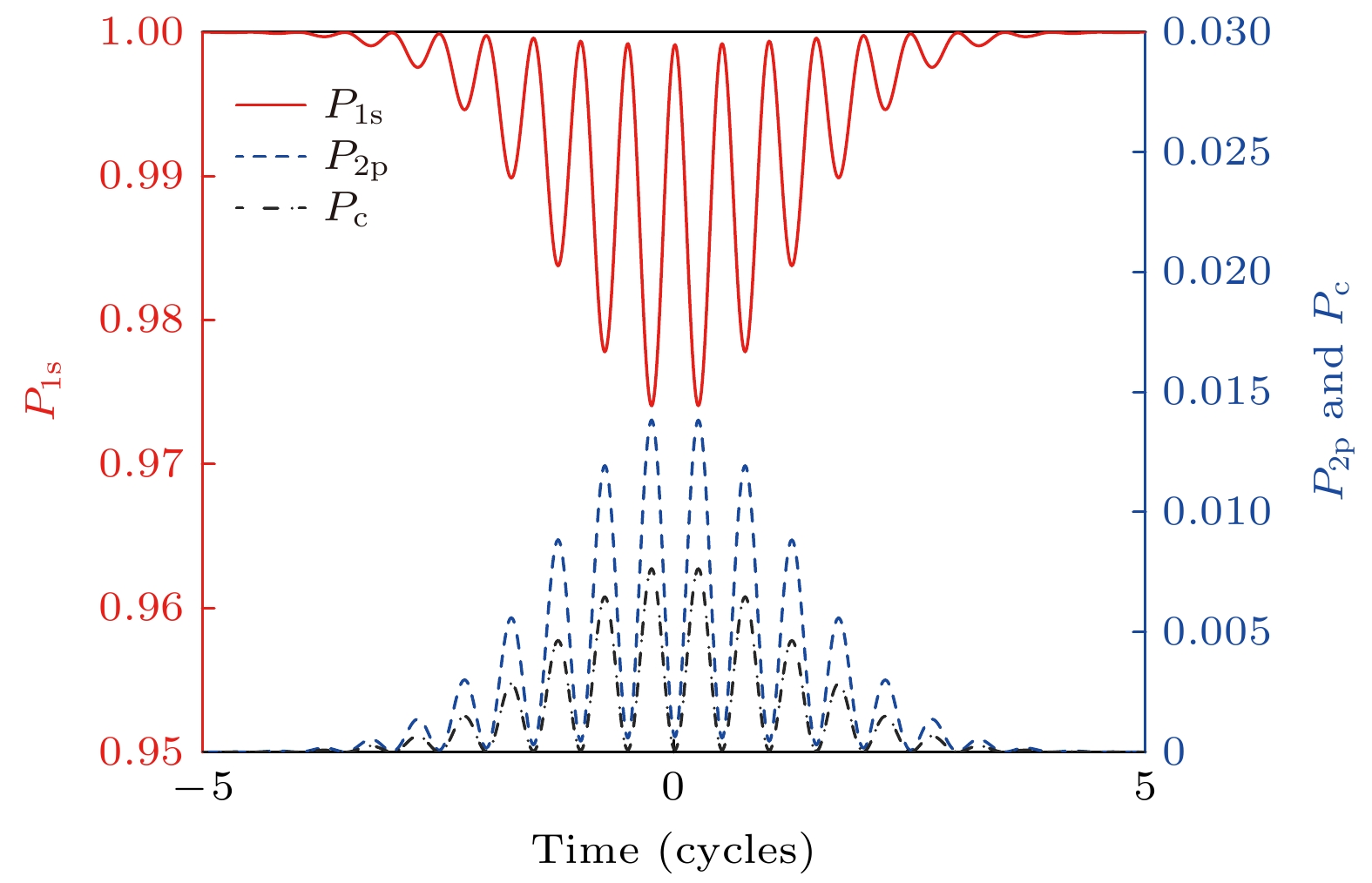
图 2 随时间演化的态概率. 左轴为基态$ \left |1 {\mathrm{s}} \right \rangle $, 右轴为激发态$ \left | 2 {\mathrm{p}} \right \rangle $与连续态$ \left | {\mathrm{c}} \right \rangle $的概率分布
Fig. 2. Time evolution of state probabilities. The left axis corresponds to the ground state $ \left |1 {\mathrm{s}} \right \rangle $, and the right axis shows the probabilities of the excited state $ \left | 2{\mathrm{ p }}\right \rangle $ and continuum state $ \left | {\mathrm{c}} \right \rangle $.
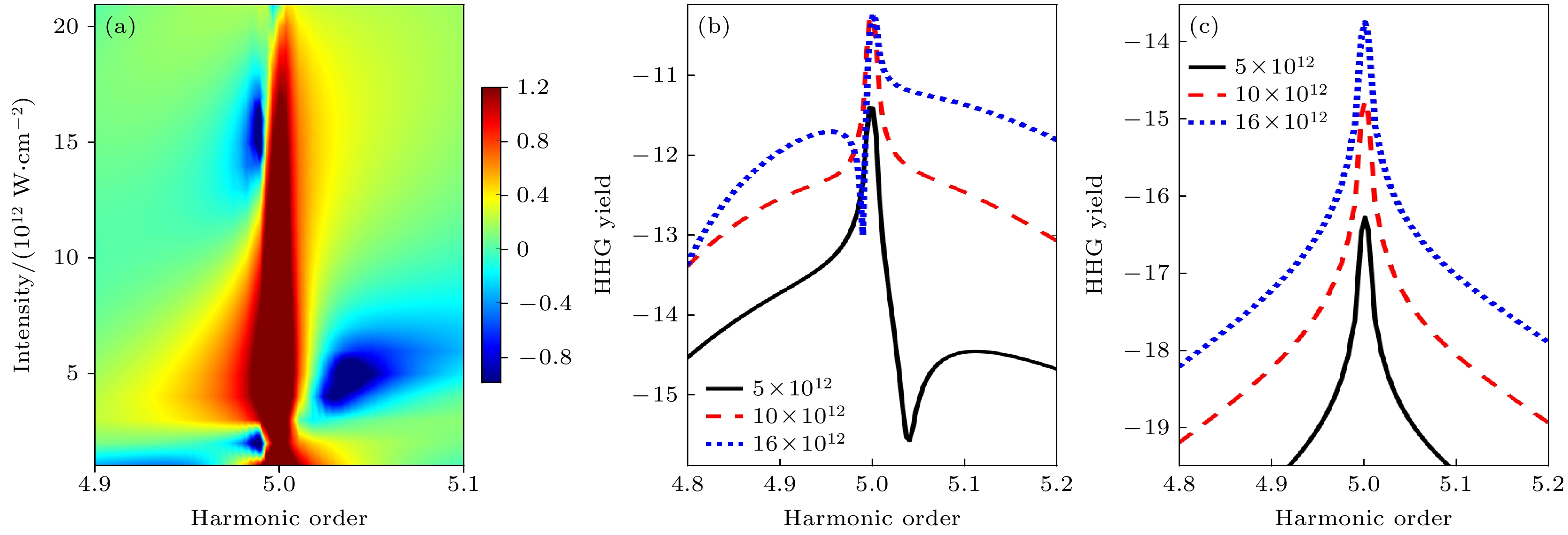
图 3 (a)归一化的第5次谐波强度随激光强度变化的谱图, 激光强度从1012 W·cm–2扫描至2 × 1013 W·cm–2; (b)对应三种典型强度下的谱线形; (c)使用简化二能级模型所得结果, 仅包含$ \left | 1 {\mathrm{s}} \right \rangle \rightarrow \left | 2 {\mathrm{p}} \right \rangle $偶极路径
Fig. 3. (a) Spectral map of normalized fifth harmonic intensity versus laser intensity scanned from 1012 W·cm–2 to 2 × 1013 W·cm–2; (b) spectral line shapes at three representative intensities; (c) results obtained using a simplified two-level model considering only the dipole $ \left | 1 {\mathrm{s }}\right \rangle \rightarrow \left | 2 {\mathrm{p}} \right \rangle $ transition pathway.
-
[1] Fano U 1961 Phys. Rev. 124 1866
Google Scholar
[2] Kobayashi K, Aikawa H, Katsumoto S, Iye Y 2002 Phys. Rev. Lett. 88 256806
Google Scholar
[3] Wang Y, Liao L, Hu T, Luo S, Wu L, Wang J, Zhang Z, Xie W, Sun L, Kavokin A V, Shen X, Chen Z 2017 Phys. Rev. Lett. 118 063602
Google Scholar
[4] Karmakar S, Kumar D, Varshney R K, Chowdhury D R 2020 Opt. Lett. 45 3386
Google Scholar
[5] Ott C, Aufleger L, Ding T, et al. 2019 Phys. Rev. Lett. 123 163201
Google Scholar
[6] Fasshauer E, Madsen L B 2020 Phys. Rev. A 101 043414
Google Scholar
[7] Wickenhauser M, Burgdörfer J, Krausz F, Drescher M 2005 Phys. Rev. Lett. 94 023002
Google Scholar
[8] Themelis S I, Lambropoulos P, Meyer M 2004 J. Phys. B: At. Mol. Opt. Phys. 37 4281
Google Scholar
[9] Tong X M, Lin C D 2005 Phys. Rev. A 71 033406
Google Scholar
[10] Zhao Z X, Lin C D 2005 Phys. Rev. A 71 060702
Google Scholar
[11] Wang H, Chini M, Chen S, Zhang C H, He F, Cheng Y, Wu Y, Thumm U, Chang Z 2010 Phys. Rev. Lett. 105 143002
Google Scholar
[12] Kaldun A, Ott C, Blättermann A, Laux M, Meyer K, Ding T, Fischer A, Pfeifer T 2014 Phys. Rev. Lett. 112 103001
Google Scholar
[13] Kaldun A, Blättermann A, Stooß V, Donsa S, Wei H, Pazourek R, Nagele S, Ott C, Lin C D, Burgdörfer J, Pfeifer T 2016 Science 354 738
Google Scholar
[14] Peng P, Marceau C, Hervé M, Corkum P B, Naumov A Y, Villeneuve D M 2019 Nat. Commun. 10 5269
Google Scholar
[15] Stooß V, Birk P, Blättermann A, Hartmann M, Borisova G D, Ott C, Pfeifer T 2020 Phys. Rev. Res. 2 032041
Google Scholar
[16] Harkema N, Cariker C, Lindroth E, Argenti L, Sandhu A 2021 Phys. Rev. Lett. 127 023202
Google Scholar
[17] Peng P, Mi Y H, Lytova M, Britton M, Ding X Y, Naumov A Y, Corkum P B, Villeneuve D M 2022 Nat. Photonics 16 4551
Google Scholar
[18] Serov V V, Kheifets A S 2024 Phys. Rev. A 110 043107
Google Scholar
[19] Han M, Liang H, Ji J B, Sum L C, Ueda K, Rost J M, Wörner H J 2025 Ultrafast Science 5 0091
Google Scholar
[20] Lewenstein M, Balcou P, Ivanov M Y, L'Huillier A, Corkum P B 1994 Phys. Rev. A 49 2117
Google Scholar
[21] Soifer H, Botheron P, Shafir D, Diner A, Raz O, Bruner B D, Mairesse Y, Pons B, Dudovich N 2010 Phys. Rev. Lett. 105 143904
Google Scholar
[22] Yost D C, Schibli T R, Ye J, Tate J L, Hostetter J, Gaarde M B, Schafer K J 2009 Nat. Phys. 5 815820
Google Scholar
[23] Hostetter J A, Tate J L, Schafer K J, Gaarde M B 2010 Phys. Rev. A 82 023401
Google Scholar
[24] Xiong W H, Geng J W, Tang J Y, Peng L Y, Gong Q 2014 Phys. Rev. Lett. 112 233001
Google Scholar
[25] Xiong W H, Jin J Z, Peng L Y, Gong Q 2017 Phys. Rev. A 96 023418
Google Scholar
[26] Camp S, Schafer K J, Gaarde M B 2015 Phys. Rev. A 92 013404
Google Scholar
[27] Li P C, Sheu Y L, Laughlin C, Chu S I 2015 Nat. Commun. 6 7178
Google Scholar
[28] Chu W C, Travers J C, Russell P S J 2016 New J. Phys. 18 023018
Google Scholar
[29] Beaulieu S, Camp S, Descamps D, Comby A, Wanie V, Petit S, Légaré F, Schafer K J, Gaarde M B, Catoire F, Mairesse Y 2016 Phys. Rev. Lett. 117 203001
Google Scholar
[30] Du L L, Wang G L, Li P C, Zhou X X, Zhao Z X 2018 Phys. Rev. A 97 023404
Google Scholar
[31] Guo Q L, Li P C, Zhou X X, Chu S I 2018 Opt. Commun. 410 262
Google Scholar
[32] Wang B, Zhang Y, Lan P, Zhai C, Li M, Zhu X, Chen J, Lu P, Lin C D 2021 Phys. Rev. A 103 053119
Google Scholar
[33] Park T J, Light J C 1986 J. Chem. Phys. 85 5870
Google Scholar
[34] Burnett K, Reed V C, Cooper J, Knight P L 1992 Phys. Rev. A 45 3347
Google Scholar
[35] Sundaram B, Milonni P W 1990 Phys. Rev. A 41 6571
Google Scholar
[36] Figueira de Morisson Faria C, Dörr M, Sandner W 1998 Phys. Rev. A 58 2990
Google Scholar
[37] Figueira de Morisson Faria C, Rotter I 2002 Phys. Rev. A 66 013402
Google Scholar
[38] Bickel W S, Goodman A S 1966 Phys. Rev. 148 1
Google Scholar
[39] Bo L, Rujiang L, Jiahui F, Qun W, Kuang Z, Wan C, Zhefei W, Ruyu M 2016 Sci. Rep. 6 31884
Google Scholar
[40] Iizawa M, Kosugi S, Koike F, Azuma Y 2021 Phys. Scr. 96 055401
Google Scholar
下载:
计量
- 文章访问数: 250
- PDF下载量: 10
- 被引次数: 0
