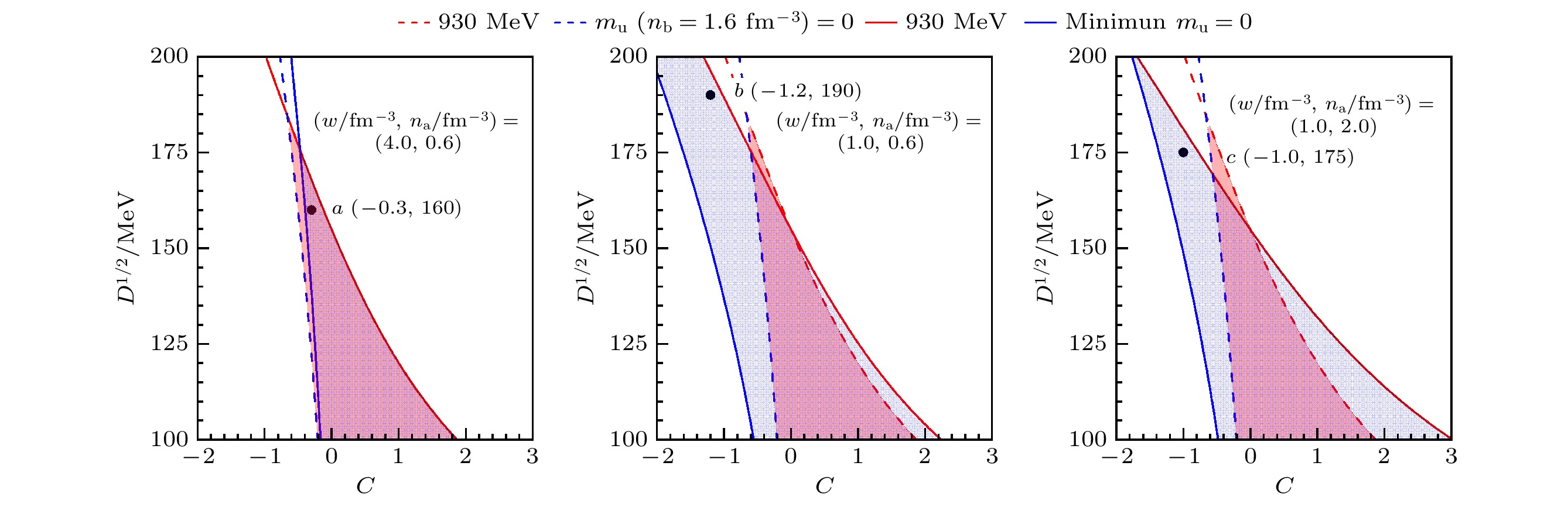
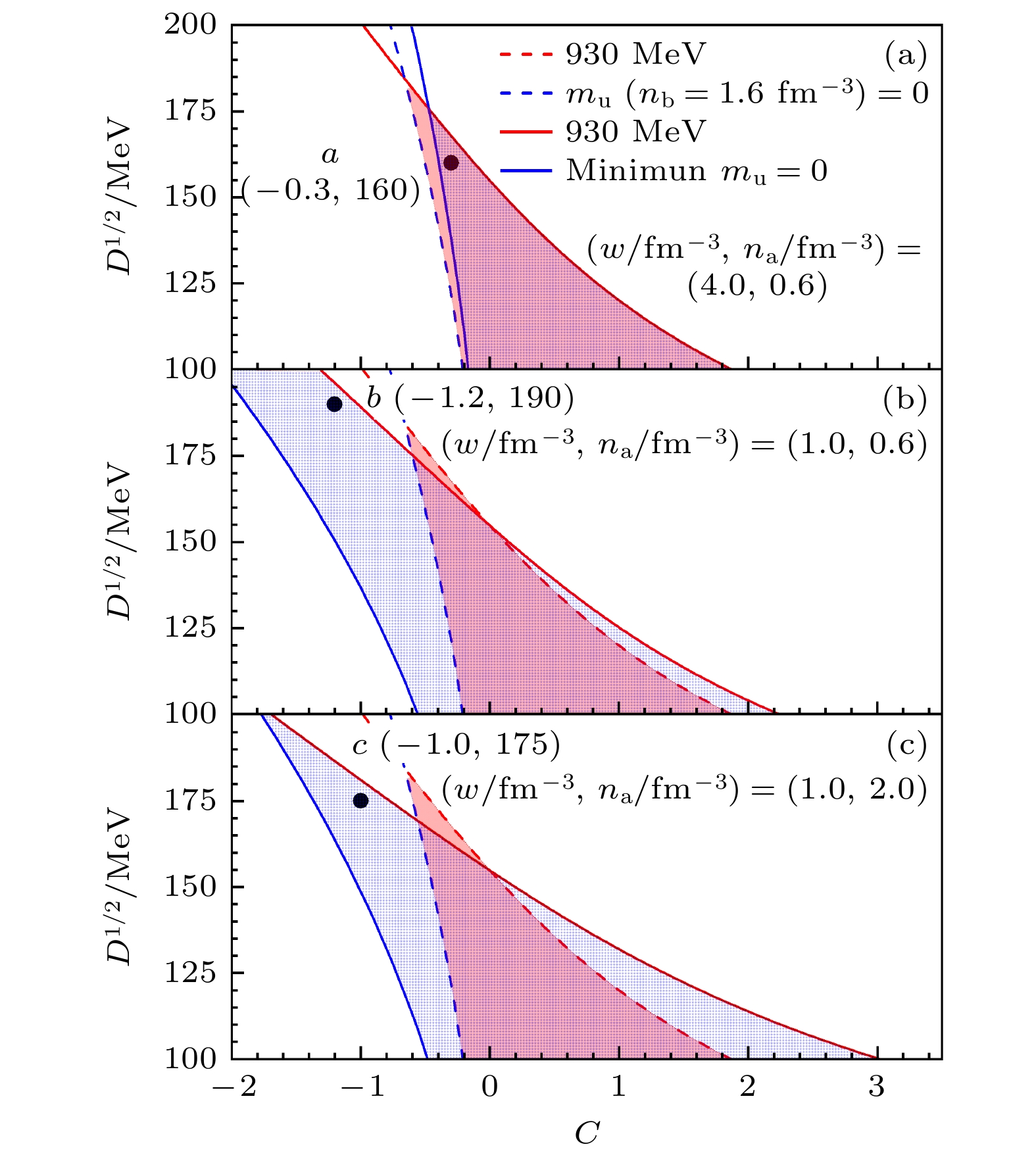
-
奇异夸克物质(strange quark matter, SQM)被认为是强相互作用的真正基态, 然而近期有研究表明普通夸克物质(u-d quark matter, u-d QM)也有可能是强相互作用的基态. 通过在夸克质量标度中采用伍兹-萨克森势(Woods-Saxon potential)型的衰减因子, 基于等效质量模型对u-d QM状态方程的计算结果表明, 衰减因子的引入增大了u-d QM稳定存在的参数窗口, 使得普通夸克星(u-d quark star, u-d QS)的质量在满足2倍太阳质量的前提下, 同时满足潮汐形变$\varLambda_{1.4} \in [70,580]$, 该计算结果符合目前的相关天文观测数据, 因此脉冲星本质上有可能是u-d QM构成的u-d QS. 本文结果为理解脉冲星的本质提供了一种可能, 也进一步加深了对强相互作用的理解.Strange quark matter (SQM) is considered to be the true ground state of the strong interactions, but recent studies have shown that ordinary quark matter (u-d quark matter, u-d QM) may also be the ground state of the strong interactions. By inserting an attenuation factor of Woods-Saxon potential type into the quark mass scaling, the resulting calculations of equation of state of u-d QM based on equiv-particle model show that the stability window of model parameters for stable u-d QM can be significantly enlarged with proper model parameters, which can be seen in the following figure. In this figure, the red solid and dashed lines represent the curves of $ \sqrt{D} $ versus C with and without attenuation factor, respectively, when the minimum value of the average energy per baryon is set to 930 MeV; the blue solid and dashed lines represent the curves of $ \sqrt{D} $ versus C with and without attenuation factor, respectively, when $ m_\mathrm{u}=0 $. Thereby, the red and blue shaded areas are the absolute stable regions of u-d QM without and with attenuation factor in mass scaling. It is obvious that with the attenuation factor and proper model parameters, the absolute stable region (blue shaded area) for u-d QM can be much larger than that without the attenuation factor (red shaded area). The introduction of the attenuation factor allows the maximum mass of ordinary quark star (u-d quark star, u-d QS) to be larger than twice the solar mass, while the tidal deformability satisfies $ \varLambda_{1.4} \in [70,580] $, which is consistent with the current astronomical observations. Therefore, the pulsars may be essentially the u-d QSs. This result provides a possibility for understanding the nature of pulsars, and it also further deepens the understanding of the strong interactions.
-
Keywords:
- quark matter /
- quark star /
- equation of state /
- tidal deformability
[1] Peng G X, Li A, Lombardo U 2008 Phys. Rev. C 77 065807
Google Scholar
[2] Weissenborn S, Sagert I, Pagliara G, Hempel M, Schaffner-Bielich J 2011 Astrophys. J. 740 L14
Google Scholar
[3] Clemente F D, Casolino M, Drago A, Lattanzi M, Ratti C 2025 Mon. Not. R. Astron. Soc. 537 1056
Google Scholar
[4] Li C M, Zheng H R, Zuo S Y, Zhao Y P, Wang F, Huang Y F 2025 Astrophys. J. 980 231
Google Scholar
[5] Song X Y 2025 Phys. Rev. D 111 063018
Google Scholar
[6] Zhang C 2020 Phys. Rev. D 101 043003
Google Scholar
[7] Xu J F, Peng G X, Liu F, Hou D F, Chen L W 2015 Phys. Rev. D 92 025025
Google Scholar
[8] Xu R X 2003 Astrophys. J. 596 L59
Google Scholar
[9] Peng G X, Chiang H C, Zou B S, Ning P Z, Luo S J 2000 Phys. Rev. C 62 025801
Google Scholar
[10] Klähn T, Fischer T 2015 Astrophys. J. 810 134
Google Scholar
[11] Xia T, He L Y, Zhuang P F 2013 Phys. Rev. D 88 056013
Google Scholar
[12] Wen X J, Feng Z Q, Li N, Peng G X 2009 J. Phys. G 36 025011
Google Scholar
[13] Li B L, Cui Z F, Yu Z H, Yan Y, An S, Zong H S 2019 Phys. Rev. D 99 043001
Google Scholar
[14] Zhang C, Gao Y, Xia C J, Xu R X 2023 Phys. Rev. D 108 063002
Google Scholar
[15] Xia C J, Peng G X, Chen S W, Lu Z Y, Xu J F 2014 Phys. Rev. D 89 105027
Google Scholar
[16] Chen S W, Gao L, Peng G X 2012 Chin. Phys. C 36 947
Google Scholar
[17] Xu J F, Cui L, Lu Z Y, Xia C J, Peng G X 2023 Nucl. Sci. Tech. 34 171
Google Scholar
[18] Demorest P, Pennucci T, Ransom S M, Roberts M S E, Hessels J W T 2010 Nature 467 1081
Google Scholar
[19] Antoniadis J, Freire P C C, Wex N, Tauris T M, Lynch R S, Kerkwijk M H V, Kramer M, Bassa C, Dhillon V S, Driebe T, Hessels J W T, Kaspi V M, Kondratiev V I, Langer N, Marsh T R, Mclaughlin M A, Pennucci T T, Ransom S M, Stairs I H, Leeuwen J V, Verbiest P W, Whelan D G 2013 Science 340 1233232
Google Scholar
[20] Cromartie H T, Fonseca E, Ransom S M, Demorest P B, Arzoumanian Z, Blumer H, Brook P R, DeCesar M E, Dolch T, Ellis J A, Ferdman R D, Ferrara E C, Garver-Daniels N, Gentile P A, Jones M L, Lam M T, Lorimer D R, Lynch R S, McLaughlin M A, Ng C, Nice D J, Pennucci T T, Spiewak R, Stairs I H, Stovall K, Swiggum J K, Zhu W W 2020 Nat. Astron. 4 72
Google Scholar
[21] Fonseca E, Cromartie H T, Pennucci T T, Ray P S, Kirichenko A Y, Ransom S M, Demorest P B, Stairs I H, Arzoumanian Z, Guillemot L, Parthasarathy A, Kerr M, Cognard I, Baker P T, Blumer H, Brook P R, DeCesar M, Dolch T, Dong F A, Ferrara E C, Fiore W, Garver-Daniels N, Good D C, Jennings R, Jones M L, Kaspi V M, Lam M T, Lorimer D R, Luo J, McEwen A, McKee J W, McLaughlin M A, McMann N, Meyers B W, Naidu A, Ng C, Nice D J, Pol N, Radovan H A, ShapiroAlbert B, Tan C M, Tendulkar S P, Swiggum J K, Wahl H M, Zhu W W 2021 Astrophys. J. Lett. 915 L12
Google Scholar
[22] Abbott R, Abbott T D, Abraham S, et al, LIGO Scientific and Virgo Collaboration 2020 Astrophys. J. Lett. 896 L44
Google Scholar
[23] LIGO Scientific and Virgo Collaboration, Abbott B P, et al. 2016 Phys. Rev. Lett. 116 061102
Google Scholar
[24] LIGO Scientific and Virgo Collaboration, Abbott B P, et al. 2017 Astrophys. J. 848 L12
Google Scholar
[25] LIGO Scientific and Virgo Collaboration, Abbott B P, et al. 2018 Phys. Rev. Lett. 121 161101
Google Scholar
[26] Witten E 1984 Phys. Rev. D 30 272
Google Scholar
[27] Farhi E, Jaffe R L 1984 Phys. Rev. D 30 2379
Google Scholar
[28] Holdom B, Ren J, Zhang C 2018 Phys. Rev. Lett. 120 222001
Google Scholar
[29] Wang J T, Peng G X 2023 Int. J. Mod. Phys. E 32 2350033
Google Scholar
[30] Fowler G, Raha S, Weiner R 1981 Z. Phys. C 9 271
Google Scholar
[31] Peng G X, Chiang H C, Yang J J, Li L, Liu B 1999 Phys. Rev. C 61 015201
Google Scholar
[32] Wen X J, Zhong X H, Peng G X, Shen P N, Ning P Z 2005 Phys. Rev. C 72 015204
Google Scholar
[33] Chen H M, Xia C J, Peng G X 2022 Chin. Phys. C 46 055102
Google Scholar
[34] Damour T, Nagar A 2009 Phys. Rev. D 80 084035
Google Scholar
[35] Fonseca E, Pennucci T T, Ellis J A, Stairs I H, Nice D J, Ransom S M, Demorest P B, Arzoumanian Z, Crowter K, Dolch T, Ferdman R D, Gonzalez M E, Jones G, Jones M L, Lam M T, Levin L, McLaughlin M A, Stovall K, Swiggum J K, Zhu W 2016 Astrophys. J. 832 167
Google Scholar
[36] Chu P C, Chen L W 2014 Astrophys. J 780 135
Google Scholar
[37] Xu J F, Xia C J, Lu Z Y, Peng G X, Zhao Y P 2022 Nucl. Sci. Tech. 33 143
Google Scholar
[38] Xu J F, Cui L, Xia C J, Lu Z Y 2024 Nucl. Phys. Rev. 41 325
Google Scholar
[39] Cui S S, Peng G X, Lu Z Y, Peng C, Xu J F 2015 Nucl. Sci. Tech. 26 040503
Google Scholar
[40] Yang L, Wen X J 2017 Phys. Rev. D 96 056023
Google Scholar
[41] Chu P C, Li X H, Ma H Y, Wang B, Dong Y M, Zhang X M 2018 Phys. Lett. B 2502 447
Google Scholar
[42] Felipe R G, Martinez A P, Rojas H P, Orsaria M 2008 Phys. Rev. C 77 015807
Google Scholar
[43] Chu P C, Liu H, Du X B 2024 Acta Phys. Sin. 73 052101
Google Scholar
[44] Pal S, Chaudhuri G 2024 Phys. Rev. D 110 123021
Google Scholar
[45] Zheng X P, Yang S H, Li J R 2003 Astrophys. J. Lett. 585 L135
Google Scholar
[46] Gourgoulhon E, Haensel P, Livine R, Paluch E, Bonazzola S, Marck J A 1999 Astron. Astrophys. 349 851
Google Scholar
[47] Yuan W L, Li A 2024 Astrophys. J. 996 3
Google Scholar
[48] Bai Y, Chen T K 2025 arXiv: 2502.20241 [hep-ph]
-
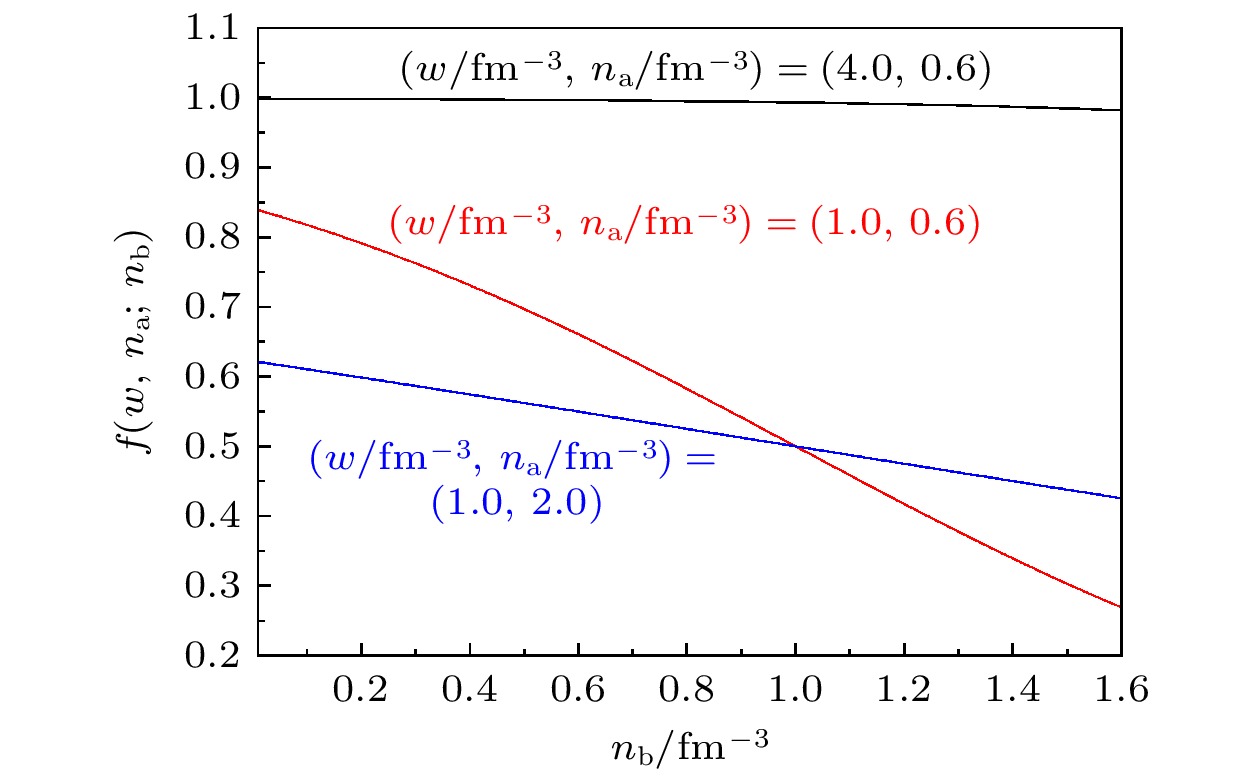
图 1 u-d QM的稳定窗口, 红色区域表示在没有考虑衰减因子时的u-d QM的稳定区域, 而蓝色区域表示衰减因子引入后u-d QM的稳定区域. 在图(a)–(c)中, 红色实线与红色虚线分别表示包含衰减因子与不包含衰减因子且当平均重子能量最小值等于930 MeV时$ \sqrt{D} $随C的变化曲线. 蓝色实线与蓝色虚线分别表示包含衰减因子与不包含衰减因子且当$ m_\mathrm{u}=0 $时$ \sqrt{D} $随C的变化曲线. 图(a)–(c)中的$ (w/\mathrm{fm}^{-3} $, $ n_{\mathrm{a}}/\mathrm{fm}^{-3}) $参数取值从上往下分别为(4.0, 0.6), (1.0, 0.6) 和(1.0, 2.0)
Fig. 1. Stability window for u-d QM, the red and blue areas are the absolute stable regions for u-d QM without and with attenuation factor in mass scaling. In the panels (a)–(c), the red solid and dashed lines represent the curves of $ \sqrt{D} $ versus C with and without attenuation factor, respectively, when the minimum value of the average energy per baryon is 930 MeV. The blue solid and dashed lines represent the curves of $ \sqrt{D} $ versus C with and without attenuation factor, respectively, when $ m_\mathrm{u}=0 $. The values of parameters $ (w/\mathrm{fm}^{-3}, n_{\mathrm{a}}/\mathrm{fm}^{-3}) $ in the panels (a)–(c) are (4.0, 0.6), (1.0, 0.6), and (1.0, 2.0) from top to bottom.
图 2 衰减因子随密度的变化曲线
Fig. 2. Curves of the attenuation factor as function of baryon number density.
图 3 平均重子能量与压强随密度的变化曲线
Fig. 3. Curves of energy per baryon and pressure as functions of baryon number density.
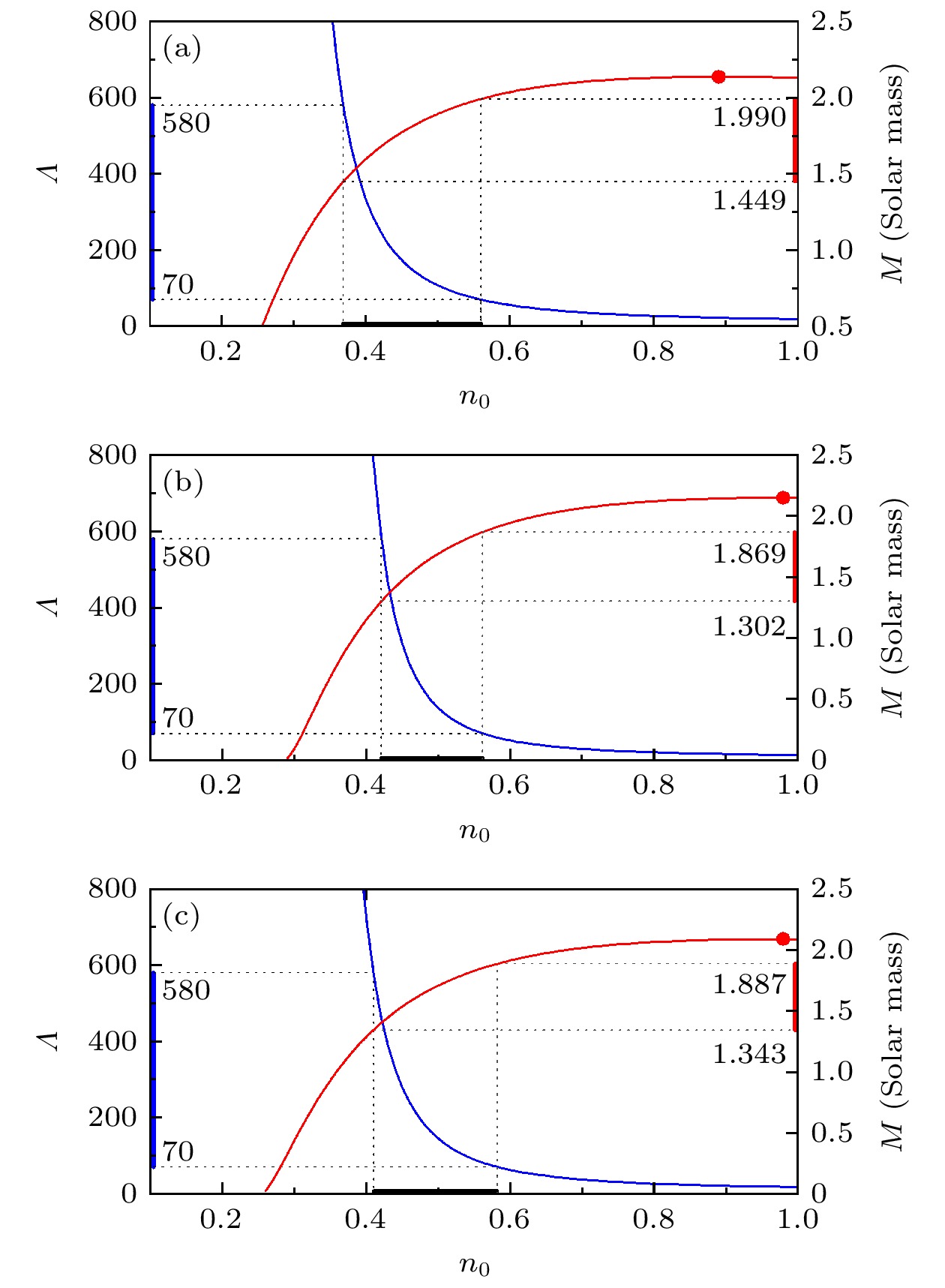
图 4 潮汐形变Λ和QS质量M随QS中心密度$ n_0 $的变化曲线, 各分图中的蓝色实线为Λ随$ n_0 $的变化曲线, 其值对应于左纵轴; 红色实线为M随$ n_0 $的变化曲线, 其值对应于右纵轴. (a)—(c)中的参数值与图1(a)—(c)中的参数值相同
Fig. 4. Curves of tidal deformability Λ and QS mass M as functions of central density $ n_0 $ of quark star, the blue solid curves corresponding to the left axis represent Λ versus $ n_0 $; the red solid curves corresponding to right axis represent M versus $ n_0 $. The parameters of panels (a)—(c) are the same with that in Fig. 1(a)—(c)
表 1 当衰减因子参数$ (w/\mathrm{fm}^{-3}, n_{\mathrm{a}}/\mathrm{fm}^{-3}) $分别取$ (4.0, 0.6), (1.0, 0.6) $和$ (1.0, 2.0) $时u-d QS的最大质量, 最大质量u-d QS的半径, 以及与潮汐形变范围$ \varLambda_{1.4} \in $$ [70, 580] $相对应的u-d QS中心密度范围和质量范围
Table 1. Maximum masses and corresponding radii of u-d QSs under $ (w/\mathrm{fm}^{-3}, n_{\mathrm{a}}/\mathrm{fm}^{-3})= (4.0, 0.6),\; (1.0, 0.6), $$ (1.0, 2.0)$, as well as the central density range and mass range of u-d quark stars for the tidal deformability range $ \varLambda_{1.4} \in [70, 580] $.
Parameter $ M_\mathrm{max}/{M}_\odot $ R/km $ n_0/\mathrm{fm}^{-3} $ $ M/{M}_\odot $ (a) 2.136 11.681 [0.369, 0.560] [1.449, 1.990] (b) 2.150 10.927 [0.421, 0.562] [1.302, 1.869] (c) 2.090 11.021 [0.410, 0.582] [1.343, 1.887] 
下载: 导出CSV
-
[1] Peng G X, Li A, Lombardo U 2008 Phys. Rev. C 77 065807
Google Scholar
[2] Weissenborn S, Sagert I, Pagliara G, Hempel M, Schaffner-Bielich J 2011 Astrophys. J. 740 L14
Google Scholar
[3] Clemente F D, Casolino M, Drago A, Lattanzi M, Ratti C 2025 Mon. Not. R. Astron. Soc. 537 1056
Google Scholar
[4] Li C M, Zheng H R, Zuo S Y, Zhao Y P, Wang F, Huang Y F 2025 Astrophys. J. 980 231
Google Scholar
[5] Song X Y 2025 Phys. Rev. D 111 063018
Google Scholar
[6] Zhang C 2020 Phys. Rev. D 101 043003
Google Scholar
[7] Xu J F, Peng G X, Liu F, Hou D F, Chen L W 2015 Phys. Rev. D 92 025025
Google Scholar
[8] Xu R X 2003 Astrophys. J. 596 L59
Google Scholar
[9] Peng G X, Chiang H C, Zou B S, Ning P Z, Luo S J 2000 Phys. Rev. C 62 025801
Google Scholar
[10] Klähn T, Fischer T 2015 Astrophys. J. 810 134
Google Scholar
[11] Xia T, He L Y, Zhuang P F 2013 Phys. Rev. D 88 056013
Google Scholar
[12] Wen X J, Feng Z Q, Li N, Peng G X 2009 J. Phys. G 36 025011
Google Scholar
[13] Li B L, Cui Z F, Yu Z H, Yan Y, An S, Zong H S 2019 Phys. Rev. D 99 043001
Google Scholar
[14] Zhang C, Gao Y, Xia C J, Xu R X 2023 Phys. Rev. D 108 063002
Google Scholar
[15] Xia C J, Peng G X, Chen S W, Lu Z Y, Xu J F 2014 Phys. Rev. D 89 105027
Google Scholar
[16] Chen S W, Gao L, Peng G X 2012 Chin. Phys. C 36 947
Google Scholar
[17] Xu J F, Cui L, Lu Z Y, Xia C J, Peng G X 2023 Nucl. Sci. Tech. 34 171
Google Scholar
[18] Demorest P, Pennucci T, Ransom S M, Roberts M S E, Hessels J W T 2010 Nature 467 1081
Google Scholar
[19] Antoniadis J, Freire P C C, Wex N, Tauris T M, Lynch R S, Kerkwijk M H V, Kramer M, Bassa C, Dhillon V S, Driebe T, Hessels J W T, Kaspi V M, Kondratiev V I, Langer N, Marsh T R, Mclaughlin M A, Pennucci T T, Ransom S M, Stairs I H, Leeuwen J V, Verbiest P W, Whelan D G 2013 Science 340 1233232
Google Scholar
[20] Cromartie H T, Fonseca E, Ransom S M, Demorest P B, Arzoumanian Z, Blumer H, Brook P R, DeCesar M E, Dolch T, Ellis J A, Ferdman R D, Ferrara E C, Garver-Daniels N, Gentile P A, Jones M L, Lam M T, Lorimer D R, Lynch R S, McLaughlin M A, Ng C, Nice D J, Pennucci T T, Spiewak R, Stairs I H, Stovall K, Swiggum J K, Zhu W W 2020 Nat. Astron. 4 72
Google Scholar
[21] Fonseca E, Cromartie H T, Pennucci T T, Ray P S, Kirichenko A Y, Ransom S M, Demorest P B, Stairs I H, Arzoumanian Z, Guillemot L, Parthasarathy A, Kerr M, Cognard I, Baker P T, Blumer H, Brook P R, DeCesar M, Dolch T, Dong F A, Ferrara E C, Fiore W, Garver-Daniels N, Good D C, Jennings R, Jones M L, Kaspi V M, Lam M T, Lorimer D R, Luo J, McEwen A, McKee J W, McLaughlin M A, McMann N, Meyers B W, Naidu A, Ng C, Nice D J, Pol N, Radovan H A, ShapiroAlbert B, Tan C M, Tendulkar S P, Swiggum J K, Wahl H M, Zhu W W 2021 Astrophys. J. Lett. 915 L12
Google Scholar
[22] Abbott R, Abbott T D, Abraham S, et al, LIGO Scientific and Virgo Collaboration 2020 Astrophys. J. Lett. 896 L44
Google Scholar
[23] LIGO Scientific and Virgo Collaboration, Abbott B P, et al. 2016 Phys. Rev. Lett. 116 061102
Google Scholar
[24] LIGO Scientific and Virgo Collaboration, Abbott B P, et al. 2017 Astrophys. J. 848 L12
Google Scholar
[25] LIGO Scientific and Virgo Collaboration, Abbott B P, et al. 2018 Phys. Rev. Lett. 121 161101
Google Scholar
[26] Witten E 1984 Phys. Rev. D 30 272
Google Scholar
[27] Farhi E, Jaffe R L 1984 Phys. Rev. D 30 2379
Google Scholar
[28] Holdom B, Ren J, Zhang C 2018 Phys. Rev. Lett. 120 222001
Google Scholar
[29] Wang J T, Peng G X 2023 Int. J. Mod. Phys. E 32 2350033
Google Scholar
[30] Fowler G, Raha S, Weiner R 1981 Z. Phys. C 9 271
Google Scholar
[31] Peng G X, Chiang H C, Yang J J, Li L, Liu B 1999 Phys. Rev. C 61 015201
Google Scholar
[32] Wen X J, Zhong X H, Peng G X, Shen P N, Ning P Z 2005 Phys. Rev. C 72 015204
Google Scholar
[33] Chen H M, Xia C J, Peng G X 2022 Chin. Phys. C 46 055102
Google Scholar
[34] Damour T, Nagar A 2009 Phys. Rev. D 80 084035
Google Scholar
[35] Fonseca E, Pennucci T T, Ellis J A, Stairs I H, Nice D J, Ransom S M, Demorest P B, Arzoumanian Z, Crowter K, Dolch T, Ferdman R D, Gonzalez M E, Jones G, Jones M L, Lam M T, Levin L, McLaughlin M A, Stovall K, Swiggum J K, Zhu W 2016 Astrophys. J. 832 167
Google Scholar
[36] Chu P C, Chen L W 2014 Astrophys. J 780 135
Google Scholar
[37] Xu J F, Xia C J, Lu Z Y, Peng G X, Zhao Y P 2022 Nucl. Sci. Tech. 33 143
Google Scholar
[38] Xu J F, Cui L, Xia C J, Lu Z Y 2024 Nucl. Phys. Rev. 41 325
Google Scholar
[39] Cui S S, Peng G X, Lu Z Y, Peng C, Xu J F 2015 Nucl. Sci. Tech. 26 040503
Google Scholar
[40] Yang L, Wen X J 2017 Phys. Rev. D 96 056023
Google Scholar
[41] Chu P C, Li X H, Ma H Y, Wang B, Dong Y M, Zhang X M 2018 Phys. Lett. B 2502 447
Google Scholar
[42] Felipe R G, Martinez A P, Rojas H P, Orsaria M 2008 Phys. Rev. C 77 015807
Google Scholar
[43] Chu P C, Liu H, Du X B 2024 Acta Phys. Sin. 73 052101
Google Scholar
[44] Pal S, Chaudhuri G 2024 Phys. Rev. D 110 123021
Google Scholar
[45] Zheng X P, Yang S H, Li J R 2003 Astrophys. J. Lett. 585 L135
Google Scholar
[46] Gourgoulhon E, Haensel P, Livine R, Paluch E, Bonazzola S, Marck J A 1999 Astron. Astrophys. 349 851
Google Scholar
[47] Yuan W L, Li A 2024 Astrophys. J. 996 3
Google Scholar
[48] Bai Y, Chen T K 2025 arXiv: 2502.20241 [hep-ph]
下载:
计量
- 文章访问数: 410
- PDF下载量: 15
- 被引次数: 0
