利用含δ介子的相对论平均场理论研究中子星潮汐形变性质

刁彬; 许妍; 黄修林; 王夷博

doi:10.7498/aps.72.20221599

摘要

开展中子星宏观性质的研究, 对于揭示中子星内部组成和结构具有重要意义. 本文基于相对论平均场理论模型, 研究了 δ 介子对传统中子星和超子星物态方程、最大质量、勒夫数和潮汐形变能力的影响. 结果表明, 对于中小质量传统中子星(或超子星), δ介子使其潮汐形变能力变强; 随着传统中子星(或超子星)质量的增加, δ介子对其潮汐形变能力影响逐渐减弱; 尤其对于大质量超子星, 含有δ介子的超子星潮汐形变能力相比不含δ介子的超子星变弱. 此外, 在相同质量下超子的存在会降低星体的潮汐形变能力, 在本文所选的参数下, 含有δ介子的星体中, 仅同时含Λ, Σ和Ξ超子的超子星潮汐形变能力能同时满足GW170817和GW190814天文观测约束. 随着与中子星相关的引力波数据逐渐增加, 将为人们判断超子星内超子种类提供一个可能的途径.

关键词:

中子星 /
δ介子 /
潮汐形变

Abstract

The research on the macroscopic properties of neutron stars is of great significance in revealing the internal composition and structure of neutron star. In this work, We analyze the influence of δ mesons on the equation of states, the maximum mass, the tidal Love numbers and the tidal deformabilities for the conventional neutron stars and the hyperon stars within the relativistic mean field theory. It is found that the presence of δ mesons can strengthen the tidal deformabilities of the low and medium-mass conventional neutron stars (or hyperon stars). However, the strengthening trends of the tidal deformabilities with δ mesons gradually weaken with the increase of the mass of the conventional neutron stars (or hyperon stars). Especially for massive hyperon stars, the tidal deformabilities of the superstars with δ mesons is weaker than the corresponding values without δ mesons. Moreover, the presence of hyperons can reduce the tidal deformabilities of stars with the same mass. For the stars containing δ mesons, only the tidal deformabilities in the hyperon stars with Λ, Σ and Ξ hyperons can satisfy the constraints of GW170817 and GW190814 events under the parameters selected in the paper. As the data about gravitational waves associated with the neutron stars gradually increase, there will be a possible way of judging the hyperon species in the hyperon stars.

Keywords:

作者及机构信息

1.
中国科学院国家天文台长春人造卫星观测站, 长春　130117

2.
中国科学院大学天文与空间科学学院, 北京　100049

通信作者: 许妍, xuy@cho.ac.cn ; 黄修林, huangxl@cho.ac.cn ; 王夷博, wangyb@cho.ac.cn

Authors and contacts

1.
Changchun Observatory, National Astronomical Observatories, Chinese Academy of Sciences, Changchun 130117, China

2.
School of Astronomy and Space Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

Corresponding author: Xu Yan, xuy@cho.ac.cn ; Huang Xiu-Lin, huangxl@cho.ac.cn ; Wang Yi-Bo, wangyb@cho.ac.cn

文章全文 : translate this paragraph

参考文献

[1]	Hewish A, Bell S J, Pilkington J D H, Scott P F, Collins R A 1968 Nature 217 709 Google Scholar
[2]	Gold T 1968 Nature 218 731 Google Scholar
[3]	赵诗艺, 刘承志, 黄修林, 王夷博, 许妍 2021 70 222601 Google Scholar Zhao S Y, Liu C Z, Huang X L, Wang Y B, Xu Y 2021 Acta Phys. Sin. 70 222601 Google Scholar
[4]	詹琼, 宋汉峰, 邰丽婷, 王江涛 2015 64 089701 Google Scholar Zhan Q, Song H F, Tai L T, Wang J T 2015 Acta Phys. Sin. 64 089701 Google Scholar
[5]	李昂, 胡金牛, 鲍世绍, 申虹, 徐仁新 2019 原子核物理评论 36 1 Google Scholar Li A, Hu J N, Bao S S, Shen H, Xu R X 2019 Nucl. Phys. Rev. 36 1 Google Scholar
[6]	来小禹, 徐仁新 2019 物理 48 554 Google Scholar Lai X Y, Xun R X 2019 Phys. 48 554 Google Scholar
[7]	龚武坤, 郭文军 2020 69 242101 Google Scholar Gong W K, Guo W J 2020 Acta Phys. Sin. 69 242101 Google Scholar
[8]	包特木巴根, 杨兴强, 喻孜 2013 62 012101 Google Scholar Bao T M E B G, Yang X Q, Yu Z 2013 Acta Phys. Sin. 62 012101 Google Scholar
[9]	Pattersons M L, Sulaksono A 2021 Eur. Phys. J. C 81 698 Google Scholar
[10]	Zhao X F 2015 Phys. Rev. C 92 055802 Google Scholar
[11]	Rather I A, Usmani, Patra S K 2021 Nucl. Phys. A 1010 122189 Google Scholar
[12]	Sun B Y, Liu Z W, Xing R Y 2019 AIP. Conf. Proc. 2127 020020 Google Scholar
[13]	Abbott B P, LIGO Scientific, Virgo Collaboration 2017 Phys. Rev. Lett. 119 161101 Google Scholar
[14]	Abbott B P, LIGO Scientific, Virgo Collaboration 2018 Phys. Rev. Lett. 121 161101 Google Scholar
[15]	Abbott R, LIGO Scientific, Virgo Collaboration 2020 Astrophys. J. Lett. 896 L44 Google Scholar
[16]	Abbott B P, LIGO Scientific, Virgo Collaboration 2020 Astrophys. J. Lett. 892 L3 Google Scholar
[17]	Abbott R, LIGO Scientific, Virgo Collaboration 2021 Astrophys. J. Lett. 915 L5 Google Scholar
[18]	Tang S P, Jiang J L, Gao W H, Wei D M 2021 Phys. Rev. D 103 063026 Google Scholar
[19]	Lim Y, Holt J W 2018 Phys. Rev. Lett. 121 062701 Google Scholar
[20]	Chatziioannou K, Haster C J Zimmerman A 2018 Phys. Rev. D 97 104036 Google Scholar
[21]	Han S, Steiner A W 2019 Phys. Rev. D 99 083014 Google Scholar
[22]	Jin H M, Xia C J, Sun T T, Peng G X 2022 Phys. Lett. B 829 137121 Google Scholar
[23]	Zhu Z Y, Zhou E P, Li A 2018 Astrophys. J. 862 98 Google Scholar
[24]	Biswas B, Nandi R Char P, Bose S 2019 Phys. Rev. D 100 044056 Google Scholar
[25]	Essick R, Landry P, Holz D E 2020 Phys. Rev. D 101 063007 Google Scholar
[26]	Miao Z Q, Li A, Dai Z G 2022 Mon. Not. R. Astron. Soc. 515 5071 Google Scholar
[27]	Huang K X, Hu J N, Zhang Y, Shen H 2022 arXiv: 2203. 12357 v1 [nucl-th]
[28]	Kubis S, Kutschera M 1997 Phys. Lett. B 399 191 Google Scholar
[29]	Yu Z, Liu G Z, Zhu M F, Xu Y, Zhao E G 2009 Chin. Phys. Lett. 26 022601 Google Scholar
[30]	Shao G Y, Liu Y X 2010 Phys. Rev. C 82 055801 Google Scholar
[31]	Qian Z, Xin R Y, Sun B Y 2018 Sci. Chin. Phys. Mech. Astron. 61 082011 Google Scholar
[32]	Roca-Maza X, Viñas X, Centelles M, Ring P, Schuck P 2016 Phys. Rev. C 93 069905 Google Scholar
[33]	Kumar B, Singh S K, Agrawal B K, Patra S K 2017 Nucl. Phys. A 996 197 Google Scholar
[34]	Bunta J K, Gmuca Š 2003 Phys. Rev. C 68 054318 Google Scholar
[35]	Xu Y, Liu G Z, Wu Y R, Zhu M F, Wang H Y, Zhao E G 2012 Plasma Sci. Technol. 14 375 Google Scholar
[36]	Xu Y, Liu G Z, Fan C B, Han X W, Zhu M F Wang H Y, Zhang X J 2013 Chin. Phys. Lett. 20 062101 Google Scholar
[37]	Liu B, Greco V, Baran V, Colonna M, Di Toro M 2002 Phys. Rev. C 65 045201 Google Scholar
[38]	Menezes D P, Providência C 2004 Phys. Rev. C 70 058801 Google Scholar
[39]	Santos A M S, Menezes D P 2004 Phys. Rev. C 69 045803 Google Scholar
[40]	Avancini S S, Brito L, Menezes D P, Providência C 2004 Phys. Rev. C 70 015203 Google Scholar
[41]	Menezes D P, Providência C 2003 Phys. Rev. C 68 035804 Google Scholar
[42]	Boguta J, Bodmer A R 1977 Nucl. Phys. 292 413 Google Scholar
[43]	Oppenheimer J R, Volkoff G M 1939 Phys. Rev. 55 378 Google Scholar
[44]	Tolman R C 1939 Phys. Rev. 55 364 Google Scholar
[45]	Thome K S 1998 Phys. Rev. D 58 124031 Google Scholar
[46]	Hinderer T 2008 Astrophys. J. 677 1216 Google Scholar
[47]	Damour T, Nagar A 2009 Phys. Rev. D 80 084035 Google Scholar
[48]	Hinderer T, Lackey B D, Lang R N, Read J S 2010 Phys. Rev. D 81 123016 Google Scholar
[49]	Liu B, Guo H, Di Toro M, et al. 2005 Eur. Phys. J. A 25 293 Google Scholar
[50]	Riley T E, Watts A L, Bogdanov S, et al. 2019 Astrophys. J. Lett. 887 L21 Google Scholar
[51]	Deller A T, Archibald A M, Brisken W F, et al. 2012 Astrophys. J. Lett. 756 L25 Google Scholar
[52]	Martinez J G, Stovall K, Freire P C C, et al. 2015 Astrophys. J. 812 143 Google Scholar

施引文献

图 1 6种情况下, 星体物态方程

Fig. 1. Equation of states for neutron star matter in the six cases.

下载: 全尺寸图片幻灯片

图 2 6种情况下, 星体质量-半径关系. 不同颜色条纹区域分别表示PSRs J1903+0327和J0453+1559的质量测量值 $ {1.666}_{-0.01}^{+0.01}{\rm{M}}_{\odot } $和 $ {1.559}_{-0.004}^{+0.004}{\rm{M}}_{\odot } $^[50,51], 橙色误差棒表示PSR J0030+0415的质量和半径测量值范围, 其质量测量值为$ {1.34}_{-0.16}^{+0.15}{\rm{M}}_{\odot } $ 和 $ {1.44}_{-0.14}^{+0.15}{\rm{M}}_{\odot } $, 相应半径值为 ${12.71}_{-1.19}^{+1.14}\;\rm{k}\rm{m}$ 和 ${13.02}_{-1.06}^{+1.24}\;\rm{k}\rm{m}$^[52]

Fig. 2. Mass - radius carves for the six equation of states. The striped areas of different colors stand for the constraints inferred from PSRs J1903+0327 and J0453+1559, and their mass measurement values are $ {1.666}_{-0.01}^{+0.01}{\rm{M}}_{\odot } $ and $ {1.559}_{-0.004}^{+0.004}{\rm{M}}_{\odot } $^[50,51], respectively. The orange error bars express the constraints on the mass-radius limits of PSR J0030+0451, and its mass measurement values are $ {1.34}_{-0.16}^{+0.15}{\rm{M}}_{\odot } $ and $ {1.44}_{-0.14}^{+0.15}{\rm{M}}_{\odot } $, the corresponding radius values are ${12.71}_{-1.19}^{+1.14}\;\rm{k}\rm{m}$ and ${13.02}_{-1.06}^{+1.24}\;\rm{k}\rm{m}$, respectively^[52]

下载: 全尺寸图片幻灯片

图 3 6种情况下, 星体勒夫数-质量关系. 其中不同颜色条纹区域分别表示PSRs J1903+0327和J0435+1559的勒夫数理论值范围, 黑色虚线表示星体质量取 $ 1.4{\rm{M}}_{\odot } $时勒夫数理论值

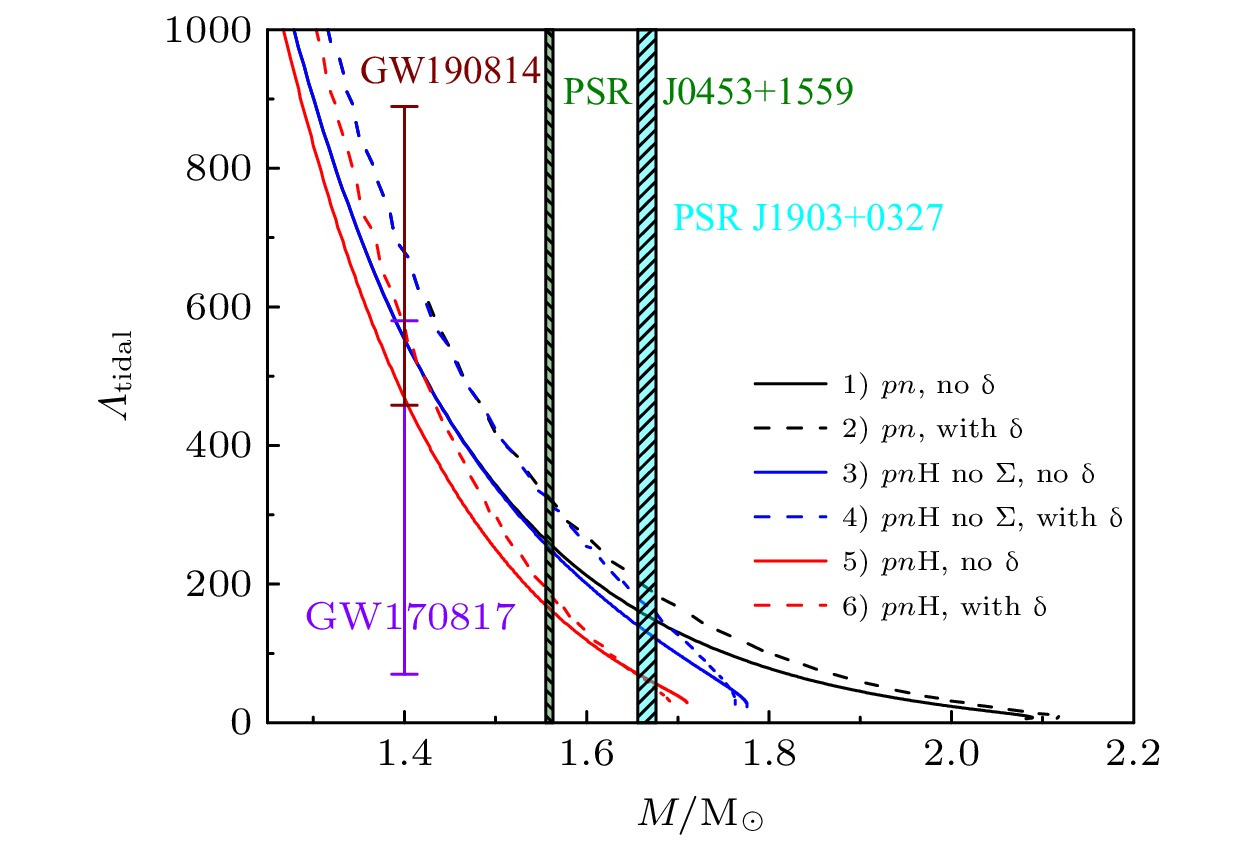
Fig. 3. Tidal Love numbers as a function of the masses for the six equation of states. The striped areas of different colors stand for the theoretical values ranges of the tidal Love numbers for PSRs J1903+0327 and J0435+1559, respectively. The vertical dashed line indicates as $M=1.4~{\rm{M}}_{\odot }$.

下载: 全尺寸图片幻灯片

图 4 6种情况下, 星体潮汐形变因子-质量关系. 不同颜色条纹区域分别表示PSRs J1903+0327和J0453+1559脉冲星的潮汐形变因子理论值范围, 彩色误差棒分别表示GW170817和GW190814对于星体潮汐形变的约束

Fig. 4. Tidal deformabilities as a function of the masses for the six equation of states. The different colors striped areas stand for the theoretical values of the tidal deformabilities for PSRs J1903+0327 and J0751+1087, respectively. The color error bar expresses the constraints from GW170817 and GW190814 events for the tidal deformabilities.

下载: 全尺寸图片幻灯片

表 1 各参数的取值. 其中, ${f}_{i}={\left( {{g}_{i}}/{{m}_{i}}\right)}^{2}\left({\rm{f}\rm{m}}^{2}\right)$, $ i=\sigma , \omega , \rho \rm{和}\delta $. 介子质量取值如下: ${m}_{\sigma }=550\;\rm{M}\rm{e}\rm{V}$, ${m}_{\omega }=783\;\rm{M}\rm{e}\rm{V}$, ${m}_{\rho }=763\;\rm{M}\rm{e}\rm{V}$和 ${m}_{\delta }=983\;\rm{M}\rm{e}\rm{V}$. 超子耦合常数表示为与核子耦合常数的比值, 即 ${x}_{i}= {{g}_{iH}}/{{g}_{i}}$, $ i=\sigma , \omega , \rho \rm{和}\delta $, 具体取值为 $ {x}_{\omega B}=0.783 $, $ {x}_{\sigma B}={x}_{\delta B}={x}_{\rho B}=0.7 $^[49]

Table 1. Parameter sets. ${f}_{i}={\left( {{g}_{i}}/{{m}_{i}}\right)}^{2}\left({\rm{f}\rm{m}}^{2}\right)$, $i=\sigma , \omega , \rho \;\rm{a}\rm{n}\rm{d}\;\delta$, we take ${m}_{\sigma }=550\;\rm{M}\rm{e}\rm{V}$, ${m}_{\omega }=783\;\rm{M}\rm{e}\rm{V}$, ${m}_{\rho }=763\;\rm{M}\rm{e}\rm{V}$ and ${m}_{\delta }=983\;\rm{M}\rm{e}\rm{V}$. The ratios of coupling constants between hyperons and nucleons can be expressed ${x}_{i}= {{g}_{iH}}/{{g}_{i}}$, $i=\sigma , \omega , \rho \;\rm{a}\rm{n}\rm{d}\;\delta$. Their values $ {x}_{\omega B} $ and $ {x}_{\sigma B} $, $ {x}_{\delta B} $, $ {x}_{\rho B} $ are 0.783 and 0.7, respectively^[49].

参数	$ {f}_{\sigma } $	$ {f}_{\omega } $	$ {f}_{\rho } $	$ {f}_{\delta } $	$ {g}_{2}/{\rm{f}\rm{m}}^{-1} $	$ {g}_{3} $
不包含$ \rm{\delta } $介子	10.33	5.42	0.95	0.00	$ 0.033{g}_{\sigma }^{3} $	$ -0.0048{g}_{\sigma }^{4} $
包含$ \rm{\delta } $介子	10.33	5.42	3.15	2.50	$ 0.033{g}_{\sigma }^{3} $	$ -0.0048{g}_{\sigma }^{4} $

下载: 导出CSV

表 2 饱和核物质性质, 饱和密度值以及在饱和密度处对称能、对称斜率和不可压缩系数值^[49]

Table 2. Properties of nuclear saturation density, namely, the values of the nuclear saturation density $ {\rho }_{0} $, the symmetry energy $ {E}_{\rm{s}\rm{y}\rm{m}} $, the symmetry energy slope L and the incompressibility $ {K}_{\rm{v}} $^[49].

参数	$ {\rho }_{0}/{\rm{f}\rm{m}}^{-3} $	$ {E}_{\rm{s}\rm{y}\rm{m}}/\rm{M}\rm{e}\rm{V} $	$ L/\rm{M}\rm{e}\rm{V} $	$ {K}_{\rm{v}}/\rm{M}\rm{e}\rm{V} $
不包含$ \rm{\delta } $介子	0.16	31.3	84	240
包含$ \rm{\delta } $介子	0.16	31.3	103	240

下载: 导出CSV

表 3 6情况下, 星体最大质量及其对应的半径、勒夫数和潮汐形变因子; 星体最大半径及其对应的质量、勒夫数和潮汐形变因子

Table 3. Values of the maximum masses M and the corresponding radii R, the tidal Love numbers $ {k}_{2} $and the tidal deformabilities Λ_tidal. Values of the maximum radii R and the corresponding masses M, the tidal Love numbers $ {k}_{2} $and the tidal deformabilities Λ_tidalwith the six cases.

	中子星最大质量处				中子星最大半径处
	$ M/{\rm{M}}_{\odot } $	$ R/\rm{k}\rm{m} $	$ {k}_{2} $	Λ_tidal	$ M/{\rm{M}}_{\odot } $	$ R/\rm{k}\rm{m} $	$ {k}_{2} $	Λ_tidal
1)	2.088	10.89	0.021	8	0.995	12.973	0.124	4405
2)	2.119	11.31	0.019	8	1.138	13.570	0.105	2417
3)	1.776	10.89	0.032	28	0.995	12.973	0.124	4405
4)	1.763	11.40	0.031	36	1.138	13.570	0.105	2417
5)	1.709	10.71	0.033	31	0.995	12.937	0.124	4405
6)	1.691	10.91	0.028	31	1.109	13.566	0.107	2791

下载: 导出CSV

表 4 6种情况下, $1.4~{\rm{M}}_{\odot }$中子星、PSRs J1903+0327和PSR J0453+1559半径、勒夫数和潮汐形变因子的理论值

Table 4. Theoretical values for the radii, the tidal Love numbers and the tidal deformabilities for the $1.4~{\rm{M}}_{\odot }$ neutron star, PSRs J1903+0327 and J0751+1087, respectively.

		R/km	$ {K}_{2} $	$\varLambda$
($ 1.4{\rm{M}}_{\odot } $中子星)	1)	12.80	0.090	545
	2)	13.51	0.085	682
	3)	12.81	0.090	548
	4)	13.51	0.085	682
	5)	12.58	0.084	468
	6)	13.25	0.079	568
PSR J1903+0327 ($ {1.666}_{-0.01}^{+0.01}{\rm{M}}_{\odot } $)	1)	[12.53, 12.56]	[0.066, 0.067]	[146, 162]
	2)	[13.26, 13.29]	[0.061, 0.064]	[180, 205]
	3)	[12.28, 12.37]	[0.060, 0.063]	[120, 140]
	4)	[13.04, 13.13]	[0.058, 0.061]	[158, 184]
	5)	[11.29, 11.48]	[0.042, 0.046]	[055, 070]
	6)	[11.49, 11.80]	[0.034, 0.039]	[050, 070]
PSR J0453+1559 ($ {1.559}_{-0.004}^{+0.004}{\rm{M}}_{\odot } $)	1)	[12.67, 12.68]	[0.076, 0.077]	[255, 265]
	2)	[13.39, 13.40]	[0.072, 0.073]	[313, 329]
	3)	[12.63, 12.64]	[0.075, 0.075]	[251, 256]
	4)	[13.37, 12.38]	[0.071, 0.073]	[309, 328]
	5)	[12.04, 12.08]	[0.061, 0.062]	[159, 169]
	6)	[12.61, 12.65]	[0.055, 0.057]	[179, 194]

下载: 导出CSV

map

[1]	Hewish A, Bell S J, Pilkington J D H, Scott P F, Collins R A 1968 Nature 217 709 Google Scholar
[2]	Gold T 1968 Nature 218 731 Google Scholar
[3]	赵诗艺, 刘承志, 黄修林, 王夷博, 许妍 2021 70 222601 Google Scholar Zhao S Y, Liu C Z, Huang X L, Wang Y B, Xu Y 2021 Acta Phys. Sin. 70 222601 Google Scholar
[4]	詹琼, 宋汉峰, 邰丽婷, 王江涛 2015 64 089701 Google Scholar Zhan Q, Song H F, Tai L T, Wang J T 2015 Acta Phys. Sin. 64 089701 Google Scholar
[5]	李昂, 胡金牛, 鲍世绍, 申虹, 徐仁新 2019 原子核物理评论 36 1 Google Scholar Li A, Hu J N, Bao S S, Shen H, Xu R X 2019 Nucl. Phys. Rev. 36 1 Google Scholar
[6]	来小禹, 徐仁新 2019 物理 48 554 Google Scholar Lai X Y, Xun R X 2019 Phys. 48 554 Google Scholar
[7]	龚武坤, 郭文军 2020 69 242101 Google Scholar Gong W K, Guo W J 2020 Acta Phys. Sin. 69 242101 Google Scholar
[8]	包特木巴根, 杨兴强, 喻孜 2013 62 012101 Google Scholar Bao T M E B G, Yang X Q, Yu Z 2013 Acta Phys. Sin. 62 012101 Google Scholar
[9]	Pattersons M L, Sulaksono A 2021 Eur. Phys. J. C 81 698 Google Scholar
[10]	Zhao X F 2015 Phys. Rev. C 92 055802 Google Scholar
[11]	Rather I A, Usmani, Patra S K 2021 Nucl. Phys. A 1010 122189 Google Scholar
[12]	Sun B Y, Liu Z W, Xing R Y 2019 AIP. Conf. Proc. 2127 020020 Google Scholar
[13]	Abbott B P, LIGO Scientific, Virgo Collaboration 2017 Phys. Rev. Lett. 119 161101 Google Scholar
[14]	Abbott B P, LIGO Scientific, Virgo Collaboration 2018 Phys. Rev. Lett. 121 161101 Google Scholar
[15]	Abbott R, LIGO Scientific, Virgo Collaboration 2020 Astrophys. J. Lett. 896 L44 Google Scholar
[16]	Abbott B P, LIGO Scientific, Virgo Collaboration 2020 Astrophys. J. Lett. 892 L3 Google Scholar
[17]	Abbott R, LIGO Scientific, Virgo Collaboration 2021 Astrophys. J. Lett. 915 L5 Google Scholar
[18]	Tang S P, Jiang J L, Gao W H, Wei D M 2021 Phys. Rev. D 103 063026 Google Scholar
[19]	Lim Y, Holt J W 2018 Phys. Rev. Lett. 121 062701 Google Scholar
[20]	Chatziioannou K, Haster C J Zimmerman A 2018 Phys. Rev. D 97 104036 Google Scholar
[21]	Han S, Steiner A W 2019 Phys. Rev. D 99 083014 Google Scholar
[22]	Jin H M, Xia C J, Sun T T, Peng G X 2022 Phys. Lett. B 829 137121 Google Scholar
[23]	Zhu Z Y, Zhou E P, Li A 2018 Astrophys. J. 862 98 Google Scholar
[24]	Biswas B, Nandi R Char P, Bose S 2019 Phys. Rev. D 100 044056 Google Scholar
[25]	Essick R, Landry P, Holz D E 2020 Phys. Rev. D 101 063007 Google Scholar
[26]	Miao Z Q, Li A, Dai Z G 2022 Mon. Not. R. Astron. Soc. 515 5071 Google Scholar
[27]	Huang K X, Hu J N, Zhang Y, Shen H 2022 arXiv: 2203. 12357 v1 [nucl-th]
[28]	Kubis S, Kutschera M 1997 Phys. Lett. B 399 191 Google Scholar
[29]	Yu Z, Liu G Z, Zhu M F, Xu Y, Zhao E G 2009 Chin. Phys. Lett. 26 022601 Google Scholar
[30]	Shao G Y, Liu Y X 2010 Phys. Rev. C 82 055801 Google Scholar
[31]	Qian Z, Xin R Y, Sun B Y 2018 Sci. Chin. Phys. Mech. Astron. 61 082011 Google Scholar
[32]	Roca-Maza X, Viñas X, Centelles M, Ring P, Schuck P 2016 Phys. Rev. C 93 069905 Google Scholar
[33]	Kumar B, Singh S K, Agrawal B K, Patra S K 2017 Nucl. Phys. A 996 197 Google Scholar
[34]	Bunta J K, Gmuca Š 2003 Phys. Rev. C 68 054318 Google Scholar
[35]	Xu Y, Liu G Z, Wu Y R, Zhu M F, Wang H Y, Zhao E G 2012 Plasma Sci. Technol. 14 375 Google Scholar
[36]	Xu Y, Liu G Z, Fan C B, Han X W, Zhu M F Wang H Y, Zhang X J 2013 Chin. Phys. Lett. 20 062101 Google Scholar
[37]	Liu B, Greco V, Baran V, Colonna M, Di Toro M 2002 Phys. Rev. C 65 045201 Google Scholar
[38]	Menezes D P, Providência C 2004 Phys. Rev. C 70 058801 Google Scholar
[39]	Santos A M S, Menezes D P 2004 Phys. Rev. C 69 045803 Google Scholar
[40]	Avancini S S, Brito L, Menezes D P, Providência C 2004 Phys. Rev. C 70 015203 Google Scholar
[41]	Menezes D P, Providência C 2003 Phys. Rev. C 68 035804 Google Scholar
[42]	Boguta J, Bodmer A R 1977 Nucl. Phys. 292 413 Google Scholar
[43]	Oppenheimer J R, Volkoff G M 1939 Phys. Rev. 55 378 Google Scholar
[44]	Tolman R C 1939 Phys. Rev. 55 364 Google Scholar
[45]	Thome K S 1998 Phys. Rev. D 58 124031 Google Scholar
[46]	Hinderer T 2008 Astrophys. J. 677 1216 Google Scholar
[47]	Damour T, Nagar A 2009 Phys. Rev. D 80 084035 Google Scholar
[48]	Hinderer T, Lackey B D, Lang R N, Read J S 2010 Phys. Rev. D 81 123016 Google Scholar
[49]	Liu B, Guo H, Di Toro M, et al. 2005 Eur. Phys. J. A 25 293 Google Scholar
[50]	Riley T E, Watts A L, Bogdanov S, et al. 2019 Astrophys. J. Lett. 887 L21 Google Scholar
[51]	Deller A T, Archibald A M, Brisken W F, et al. 2012 Astrophys. J. Lett. 756 L25 Google Scholar
[52]	Martinez J G, Stovall K, Freire P C C, et al. 2015 Astrophys. J. 812 143 Google Scholar

[1]	赵诗艺, 刘承志, 黄修林, 王夷博, 许妍. 强磁场对中子星转动惯量与表面引力红移的影响. , 2021, 70(22): 222601. doi: 10.7498/aps.70.20211051
[2]	龚武坤, 郭文军. 混合中子星内强子-夸克退禁闭相变. , 2020, 69(24): 242101. doi: 10.7498/aps.69.20200925
[3]	陈建玲, 王辉, 贾焕玉, 马紫微, 李永宏, 谭俊. 超强磁场下中子星壳层的电导率和磁星环向磁场欧姆衰变. , 2019, 68(18): 180401. doi: 10.7498/aps.68.20190760
[4]	高朋林, 郑皓, 孙光爱. 中子星对自旋相关轴矢量新相互作用的约束. , 2019, 68(18): 181102. doi: 10.7498/aps.68.20190477
[5]	宋冬灵, 明亮, 单昊, 廖天河. 超强磁场下电子朗道能级稳定性及对电子费米能的影响. , 2016, 65(2): 027102. doi: 10.7498/aps.65.027102
[6]	孙旭东, 陈菊华, 王永久. 磁荷对中子星质量半径比的约束. , 2013, 62(16): 160401. doi: 10.7498/aps.62.160401
[7]	王兆军, 吕国梁, 朱春花, 霍文生. 相对论简并电子气体的磁化. , 2012, 61(17): 179701. doi: 10.7498/aps.61.179701
[8]	支启军. N=28丰中子核的形变和形状共存研究. , 2011, 60(5): 052101. doi: 10.7498/aps.60.052101
[9]	王兆军, 吕国梁, 朱春花, 张军. 中子星中简并电子气体的临界磁化. , 2011, 60(4): 049702. doi: 10.7498/aps.60.049702
[10]	刘晶晶. 超强磁场对中子星外壳层核素56Fe,56Co,56Ni,56Mn和56Cr电子俘获过程中微子能量损失的影响. , 2010, 59(7): 5169-5174. doi: 10.7498/aps.59.5169
[11]	张洁, 刘门全, 魏丙涛, 罗志全. 强磁场中修正URCA过程的中微子产能率. , 2008, 57(9): 5448-5451. doi: 10.7498/aps.57.5448
[12]	戴子高, 陆埮, 彭秋和. 中子星内部非奇异-奇异夸克物质的相变. , 1993, 42(8): 1210-1215. doi: 10.7498/aps.42.1210
[13]	王青德, 陆埮. π凝聚态中的弱过程对中子星振动的阻尼效应. , 1985, 34(7): 892-900. doi: 10.7498/aps.34.892
[14]	杨慧琳, 胡诗婉, 王珮. 关于ρ介子的辐射衰变. , 1964, 20(5): 475-476. doi: 10.7498/aps.20.475
[15]	关洪. 低能π介子—核子散射. , 1964, 20(3): 207-215. doi: 10.7498/aps.20.207
[16]	彭宏安. 低能π介子—核子散射和π介子-π介子作用. , 1962, 18(12): 621-628. doi: 10.7498/aps.18.621
[17]	唐孝威. π^-介子星裂能谱仪. , 1961, 17(2): 104-107. doi: 10.7498/aps.17.104
[18]	郭硕鸿. π介子的辐射衰变. , 1960, 16(5): 299-304. doi: 10.7498/aps.16.299
[19]	周光召, 戴元本. π介子核子碰撞产生π介子的色散关系. , 1960, 16(5): 252-262. doi: 10.7498/aps.16.252
[20]	А.Ф.杜纳耶切夫, Ю.Д.布罗高舒金, 唐孝威. π^-介子星裂探测器. , 1960, 16(8): 471-478. doi: 10.7498/aps.16.471

计量

文章访问数: 3997
PDF下载量: 79
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

利用含δ介子的相对论平均场理论研究中子星潮汐形变性质