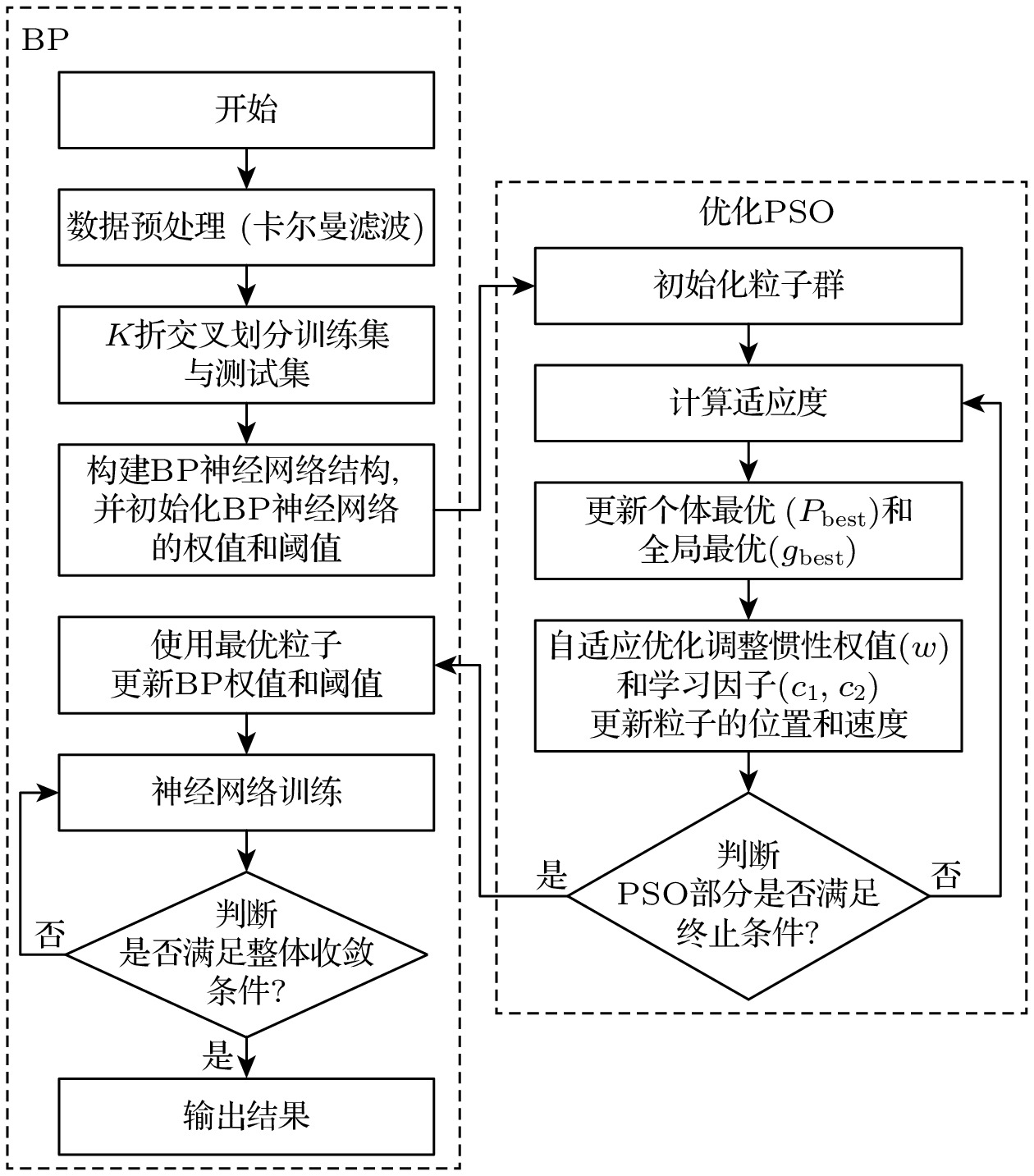
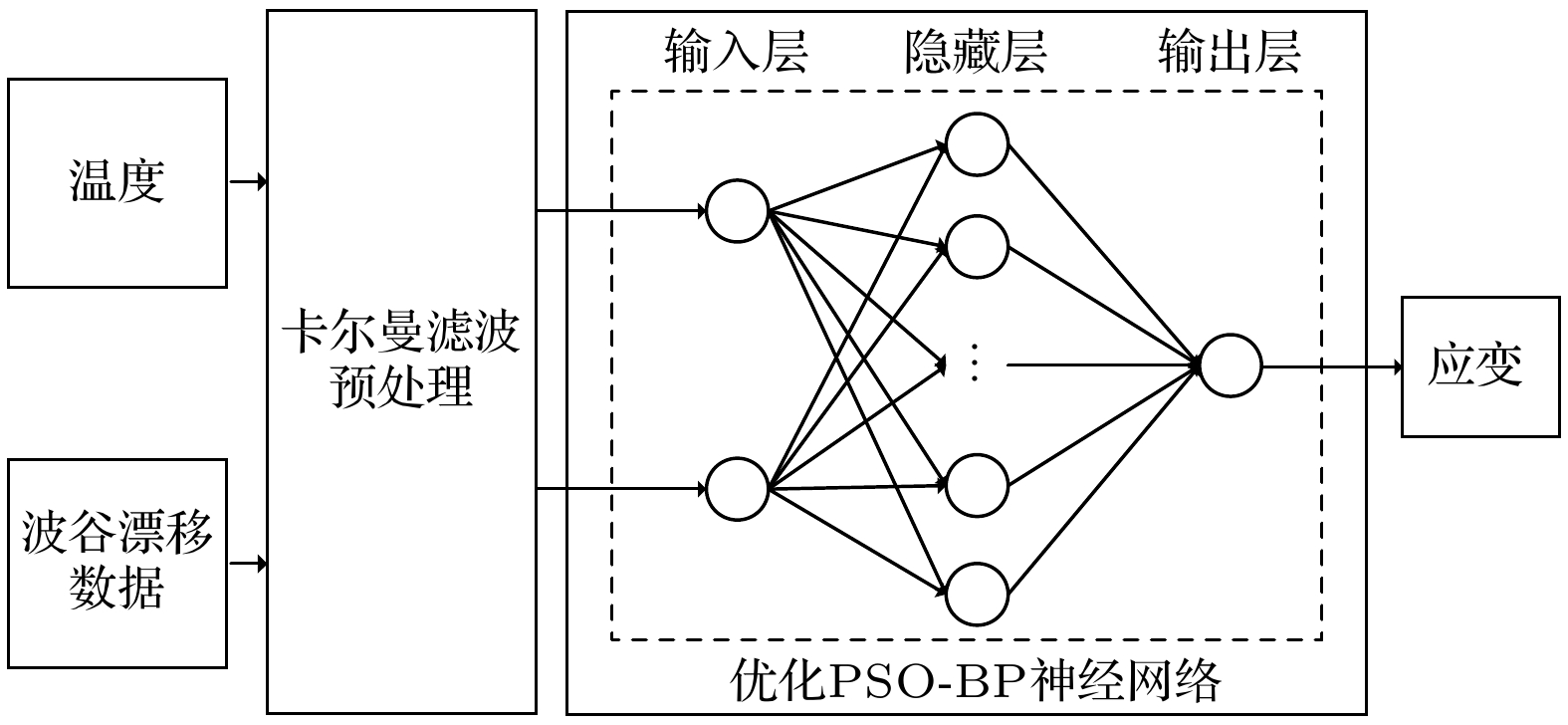
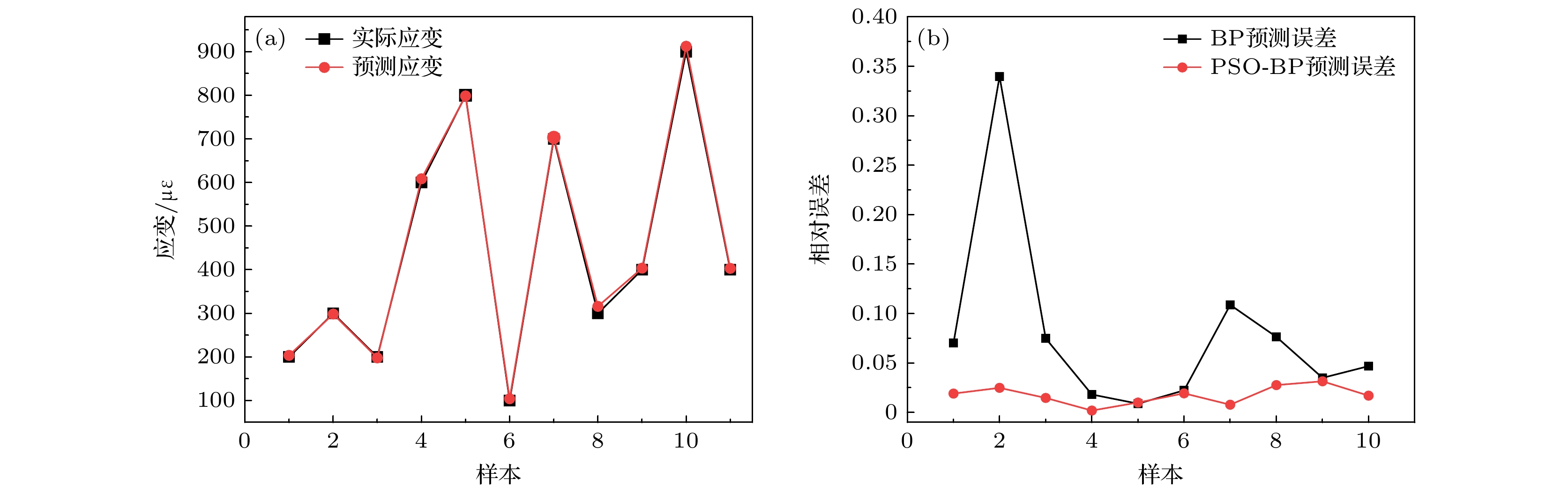
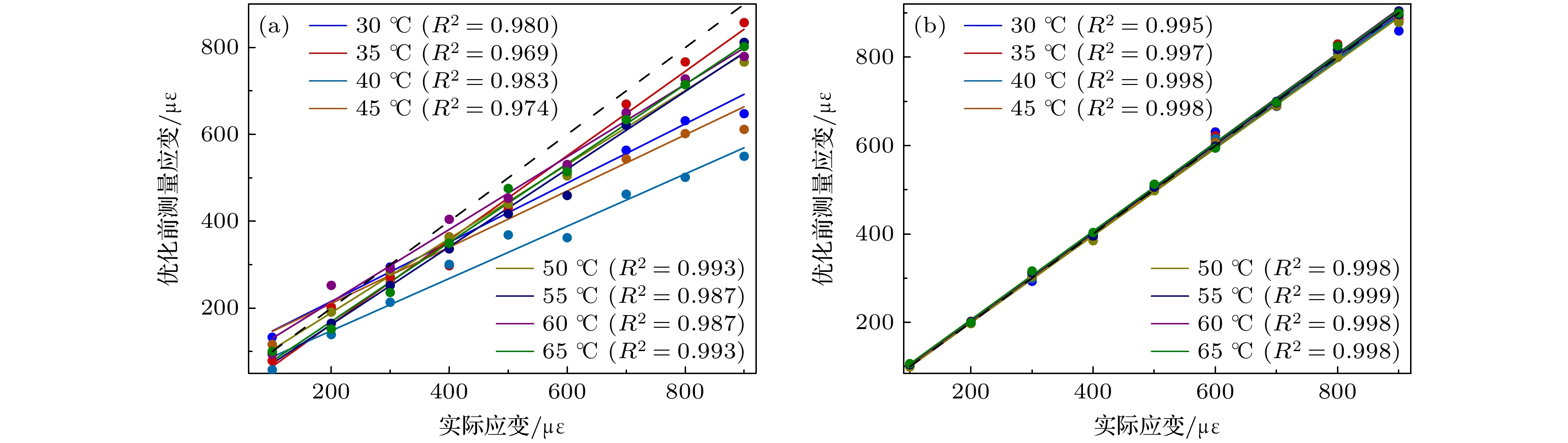
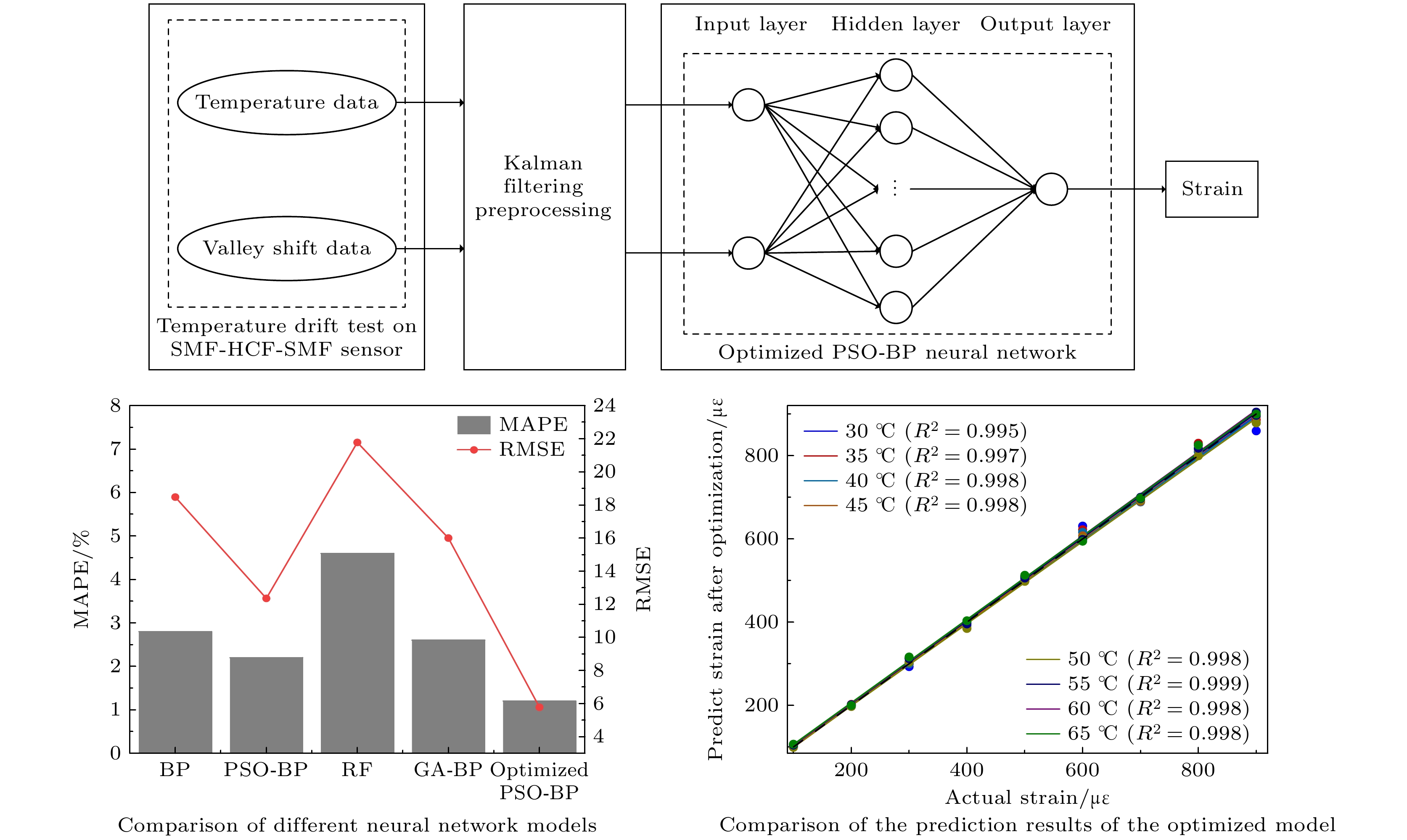
-
环境温度变化常会引起光纤法珀应变传感器的测量误差. 为有效补偿温度对测量结果的影响, 本文提出了一种优化的粒子群-反向传播(particle swarm optimization-back propagation, PSO-BP)神经网络算法. 该算法直接将温度和光纤法珀应变传感器测得的光谱峰值漂移数据作为实验样本输入, 建立温度补偿神经网络系统模型, 采用自适应调整惯性权重和学习因子动态优化调整机制, 提高了算法的全局搜索能力和局部收敛精度, 从而实现对温度干扰的有效补偿. 实验结果表明, 在整个传感器的温度测量范围内, 基于优化PSO-BP算法的平均绝对百分比误差为1.2%, 相比传统的BP算法和PSO-BP算法的平均绝对百分比误差分别改进了57.14%和45.45%, 且不同温度下R2普遍在0.995以上, 这表明模型能够在不同温度条件下准确预测应变值, 从而实现有效的温度补偿, 为低成本高精度传感系统的开发提供了新的技术途径.
-
关键词:
- 光纤传感器 /
- 优化粒子群-反向传播神经网络 /
- 温度补偿 /
- 法珀干涉
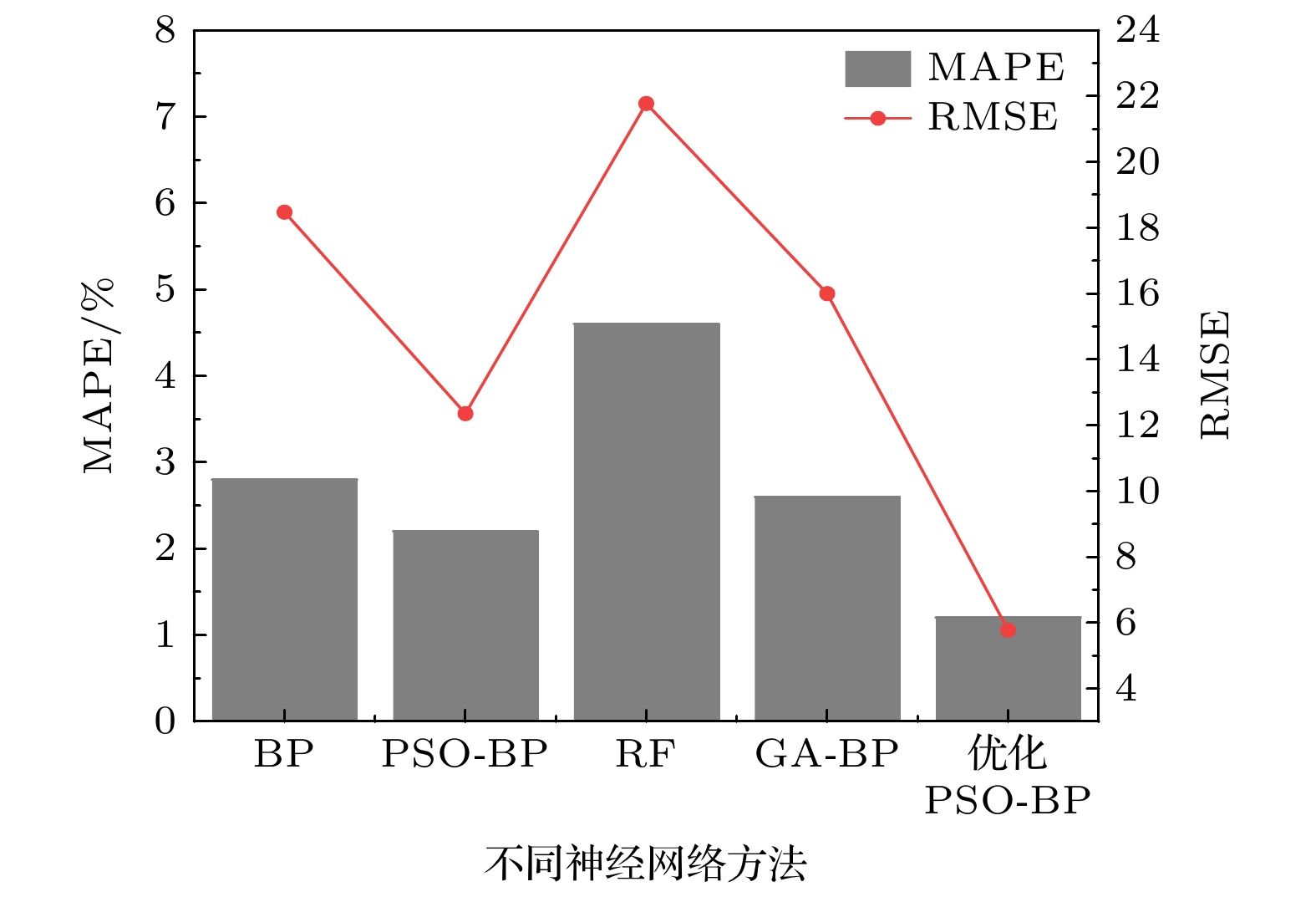
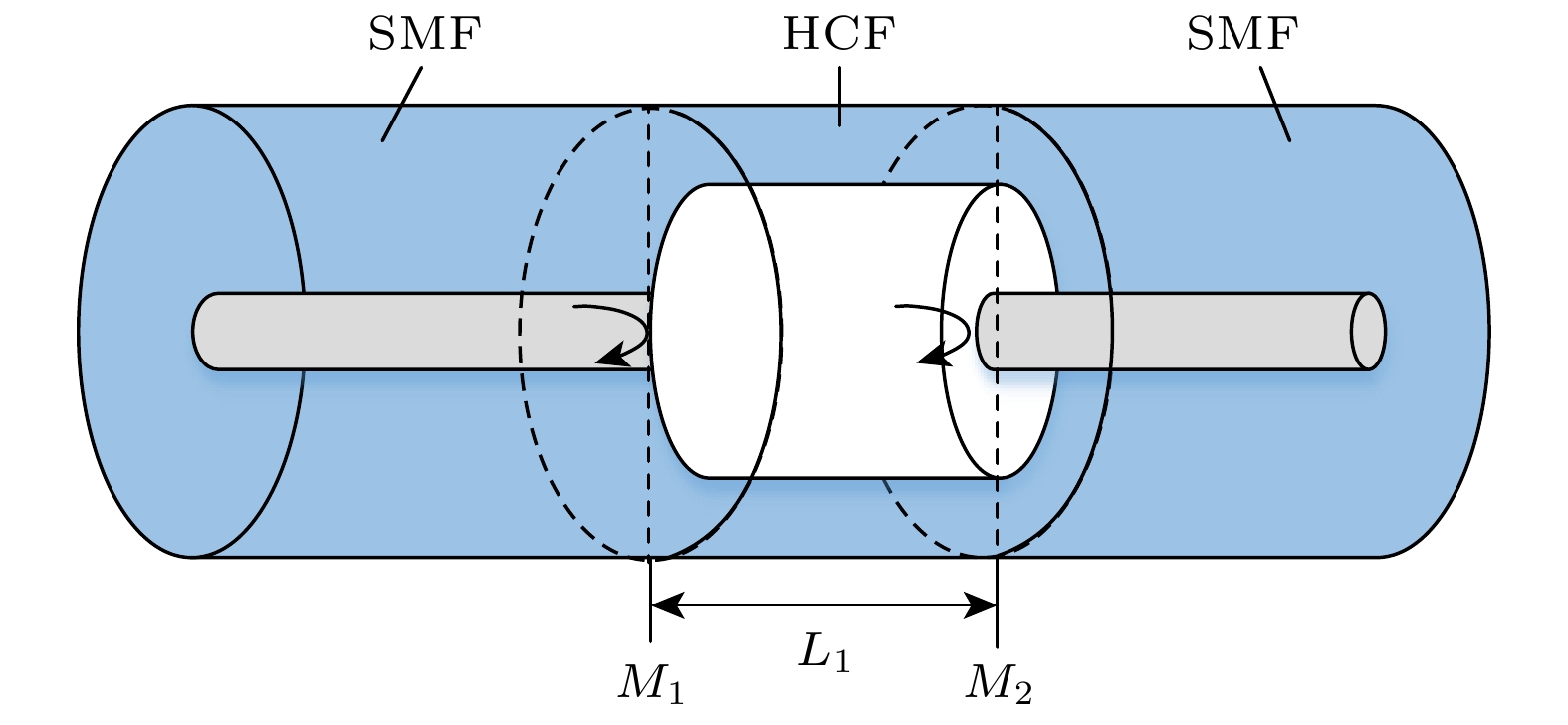
Ambient temperature fluctuations often induce measurement errors in fiber-optic Fabry-Perot strain sensors. To effectively compensate for the influence of temperature on measurement accuracy, this study proposes an optimized particle swarm optimization-back propagation (PSO-BP) neural network algorithm. The combined predictive model is applied to the monitoring data of a Fabry-Perot strain sensor based on a single-mode fiber-hollow-core fiber-single-mode fiber (SMF-HCF-SMF) structure. By preprocessing the data collected from the sensor, the temperature values and spectral valley shift data obtained from the fiber-optic Fabry-Perot strain sensor are directly used as input features to establish a temperature-compensated neural network model. Based on the traditional PSO-BP neural network algorithm, an optimization strategy incorporating adaptive adjustment of inertia weights and learning factors is employed to enhance global search capability and local convergence accuracy, thereby enabling effective compensation for temperature-induced effects. Experimental results demonstrate that in the entire temperature measurement range of the sensor, the optimized PSO-BP neural network achieves a mean absolute percentage error (MAPE) of about 1.2% and a root mean square error (RMSE) of about 5.9, significantly outperforming other methods. Comparative analysis with different model architectures reveals that compared with the BP, PSO-BP, RF, and GA-BP models, the optimized PSO-BP model improves MAPE by 57.14%, 45.45%, 73.91%, and 53.85%, respectively, while reducing RMSE by 68.11%, 52.42%, 72.94%, and 63.13%. Moreover, the coefficient of determination (R2) consistently exceeds 0.995 under various temperature conditions, indicating that the model effectively compensates for temperature-induced errors in the sensor under different thermal and strain conditions, and has excellent stability and adaptability. Therefore, the temperature compensation method proposed in this study not only offers a novel approach for improving the measurement accuracy of fiber-optic Fabry-Perot strain sensors, but also provides a valuable reference for studying the temperature compensation in related sensor technologies. Future research may further explore the applicability of this method to other types of sensors, thereby promoting the sustaining development of intelligent sensing technologies. 
-
Keywords:
- optical fiber sensor /
- optimized particle swarm optimization-back propagation neural network /
- temperature compensation /
- Fabry-Perot interference
[1] 冯德全, 罗小东, 樊伟, 朱宝辉, 乔学光 2021 光学学报 41 2106004
Google Scholar
Feng D Q, Luo X D, Fan W, Zhu B H, Qiao X G 2021 Acta Opt. Sin. 41 2106004
Google Scholar
[2] 田晨, 陈海滨, 胡锴, 张军英, 王伟 2022 光电子·激光 33 865
Google Scholar
Tian C, Chen H B, Hu K, Zhang J Y, Wang W 2022 J. Optoelectron. Laser 33 865
Google Scholar
[3] Xiao Y, Cheng J 2024 Sensors 24 7805
Google Scholar
[4] Bian Q, Podhrazsky A, Bauer C, Stadler A, Buchfellner F, Kuttler R, Jakobi M, Volk W, Koch A W, Roths J 2022 Opt. Express 30 33449
Google Scholar
[5] 芮菲, 葛益娴, 苏蕊, 倪海彬 2024 光学学报 44 1606004
Google Scholar
Rui F, Ge Y X, Su R, Ni H B 2024 Acta Opt. Sin. 44 1606004
Google Scholar
[6] 陈鸣, 常建华, 徐遥, 金澳博, 胡子怡 2023 光学学报 43 2306001
Google Scholar
Chen M, Chang J H, Xu Y, Jin A B, Hu Z Y 2023 Acta Opt. Sin. 43 2306001
Google Scholar
[7] 孙家程, 王婷婷, 戴洋, 常建华, 柯炜 2021 70 064202
Google Scholar
Sun J C, Wang T T, Dai Y, Chang J H, Ke W 2021 Acta Phys. Sin. 70 064202
Google Scholar
[8] 王雅莉, 徒芸, 涂善东, 于新海, 郭永宁, 任利杰, 陈时健 2023 仪表技术与传感器 43 26
Google Scholar
Wang Y L, Tu Y, Tu S D, Yu X H, Guo Y N, Ren L J, Chen S J 2023 Instrum. Tech. Sens. 43 26
Google Scholar
[9] Ding X, Chen N, Jin T, Zhang X D, Zhang R F 2023 Opt. Laser Technol. 162 109302
Google Scholar
[10] 赵勇, 蔡露, 李雪刚, 吕日清 2017 66 070601
Google Scholar
Zhao Y, Cai L, Li X G, Lü R Q 2017 Acta Phys. Sin. 66 070601
Google Scholar
[11] 吴倩, 张诸宇, 郭晓晨, 施伟华 2018 67 184212
Google Scholar
Wu Q, Zhang Z Y, Guo X C, Shi W H 2018 Acta Phys. Sin. 67 184212
Google Scholar
[12] Cao Y, Xu W Y, Lin B, Zhu Y, Meng F C, Zhao X T, Ding J M, Lou S Q, Wang X, He J W, Sheng X Z, Liang S 2022 Appl. Opt. 61 8212
Google Scholar
[13] 杨建宇, 梁磊, 唐浩冕, 谢官模, 徐刚 2020 光电子·激光 31 351
Google Scholar
Yang J Y, Liang L, Tang H M, Xie G M, Xu G 2020 J. Optoelectron. Laser 31 351
Google Scholar
[14] 李勇志, 金东洋, 黄文雪, 胡久龄, 景殿涛 2022 压电与声光 44 873
Google Scholar
Li Y Z, Jin D Y, Huang W X, Hu J L, Jing D T 2022 Piezoelectr. Acoustoopt. 44 873
Google Scholar
[15] 孙超, 郭乃宇, 叶力, 苗隆鑫, 曹勉, 丁建军, 严明蝶 2022 压电与声光 44 85
Google Scholar
Sun C, Guo N Y, Ye L, Miao L X, Cao M, Ding J J, Yan M D 2022 Piezoelectr. Acoustoopt 44 85
Google Scholar
[16] 孙萌萌 2023 硕士学位论文(南京: 南京信息工程大学)
Sun M M 2023 M. S. Thesis (Nanjing: Nanjing University of Information Science and Technology
[17] 张金文 2023 硕士学位论文(哈尔滨: 黑龙江大学)
Zhang J W 2023 M. S. Thesis (Harbin: Heilongjiang University
[18] Yu W, Qu H, Zhang Y 2023 Sensors 23 7823
Google Scholar
[19] Li Y J, Li Y H, Li F, Zhao B, Li Q Q 2015 Math. Probl. Eng. 2015 854945
Google Scholar
[20] Wei L X, Zhang Y, Ji L I, Ye L, Zhu X C, Fu J 2022 Energies 15 5880
Google Scholar
[21] Zhou Z W, Gong H Y, You J, Liu S B, He J L 2021 Mater. Today Commun. 28 102507
Google Scholar
[22] 周勇 2024 测绘与空间地理信息 47 217
Google Scholar
Zhou Y 2024 Geomatics & Spatial Information Technology 47 217
Google Scholar
[23] Li X, Ke S C, Li Y, Jin W, Fu X H, Fu G W, Bi W H 2024 Opt. Laser Technol. 176 110973
Google Scholar
-
图 2 传感器温度仿真反射光谱漂移图
Fig. 2. Temperature-induced drift in simulated reflectance spectra of sensors.
图 3 传感器应变测试 (a) 反射光谱漂移图; (b) 线性拟合图
Fig. 3. Sensor strain test: (a) Reflection spectrum drift map; (b) linear fitting map.
图 5 温度标定实验下不同温度光纤应变传感器的波谷漂移波长特性曲线
Fig. 5. Wavelength drift characteristics curve of fiber optic strain sensors at different temperatures under temperature calibration experiment.
图 8 优化PSO-BP神经网络结构图
Fig. 8. Structural diagram of the optimized PSO-BP neural network.
图 9 训练结果 (a) 预测输出; (b) 相对误差
Fig. 9. Training results: (a) Predicted output; (b) relative error.
图 10 不同温度下应变预测值与实际值对比图 (a) 优化前; (b) 优化后
Fig. 10. Comparison of predicted and actual strain values at different temperatures: (a) Before optimization; (b) after optimization.
表 1 不同隐藏层误差对比
Table 1. Comparison of errors for different hidden layers.
隐藏层
节点个数3 4 5 6 7 8 9 10 11 MAPE/% 1.96 2.16 1.93 1.47 2.08 1.60 1.96 1.21 1.92 
下载: 导出CSV
表 2 不同神经网络模型对比
Table 2. Comparison of different neural network models.
性能指标 BP PSO-BP RF GA-BP 优化PSO-BP MAPE/% 2.8 2.2 4.6 2.6 1.2 RMSE 18.5 12.4 21.8 16.0 5.9
下载: 导出CSV
-
[1] 冯德全, 罗小东, 樊伟, 朱宝辉, 乔学光 2021 光学学报 41 2106004
Google Scholar
Feng D Q, Luo X D, Fan W, Zhu B H, Qiao X G 2021 Acta Opt. Sin. 41 2106004
Google Scholar
[2] 田晨, 陈海滨, 胡锴, 张军英, 王伟 2022 光电子·激光 33 865
Google Scholar
Tian C, Chen H B, Hu K, Zhang J Y, Wang W 2022 J. Optoelectron. Laser 33 865
Google Scholar
[3] Xiao Y, Cheng J 2024 Sensors 24 7805
Google Scholar
[4] Bian Q, Podhrazsky A, Bauer C, Stadler A, Buchfellner F, Kuttler R, Jakobi M, Volk W, Koch A W, Roths J 2022 Opt. Express 30 33449
Google Scholar
[5] 芮菲, 葛益娴, 苏蕊, 倪海彬 2024 光学学报 44 1606004
Google Scholar
Rui F, Ge Y X, Su R, Ni H B 2024 Acta Opt. Sin. 44 1606004
Google Scholar
[6] 陈鸣, 常建华, 徐遥, 金澳博, 胡子怡 2023 光学学报 43 2306001
Google Scholar
Chen M, Chang J H, Xu Y, Jin A B, Hu Z Y 2023 Acta Opt. Sin. 43 2306001
Google Scholar
[7] 孙家程, 王婷婷, 戴洋, 常建华, 柯炜 2021 70 064202
Google Scholar
Sun J C, Wang T T, Dai Y, Chang J H, Ke W 2021 Acta Phys. Sin. 70 064202
Google Scholar
[8] 王雅莉, 徒芸, 涂善东, 于新海, 郭永宁, 任利杰, 陈时健 2023 仪表技术与传感器 43 26
Google Scholar
Wang Y L, Tu Y, Tu S D, Yu X H, Guo Y N, Ren L J, Chen S J 2023 Instrum. Tech. Sens. 43 26
Google Scholar
[9] Ding X, Chen N, Jin T, Zhang X D, Zhang R F 2023 Opt. Laser Technol. 162 109302
Google Scholar
[10] 赵勇, 蔡露, 李雪刚, 吕日清 2017 66 070601
Google Scholar
Zhao Y, Cai L, Li X G, Lü R Q 2017 Acta Phys. Sin. 66 070601
Google Scholar
[11] 吴倩, 张诸宇, 郭晓晨, 施伟华 2018 67 184212
Google Scholar
Wu Q, Zhang Z Y, Guo X C, Shi W H 2018 Acta Phys. Sin. 67 184212
Google Scholar
[12] Cao Y, Xu W Y, Lin B, Zhu Y, Meng F C, Zhao X T, Ding J M, Lou S Q, Wang X, He J W, Sheng X Z, Liang S 2022 Appl. Opt. 61 8212
Google Scholar
[13] 杨建宇, 梁磊, 唐浩冕, 谢官模, 徐刚 2020 光电子·激光 31 351
Google Scholar
Yang J Y, Liang L, Tang H M, Xie G M, Xu G 2020 J. Optoelectron. Laser 31 351
Google Scholar
[14] 李勇志, 金东洋, 黄文雪, 胡久龄, 景殿涛 2022 压电与声光 44 873
Google Scholar
Li Y Z, Jin D Y, Huang W X, Hu J L, Jing D T 2022 Piezoelectr. Acoustoopt. 44 873
Google Scholar
[15] 孙超, 郭乃宇, 叶力, 苗隆鑫, 曹勉, 丁建军, 严明蝶 2022 压电与声光 44 85
Google Scholar
Sun C, Guo N Y, Ye L, Miao L X, Cao M, Ding J J, Yan M D 2022 Piezoelectr. Acoustoopt 44 85
Google Scholar
[16] 孙萌萌 2023 硕士学位论文(南京: 南京信息工程大学)
Sun M M 2023 M. S. Thesis (Nanjing: Nanjing University of Information Science and Technology
[17] 张金文 2023 硕士学位论文(哈尔滨: 黑龙江大学)
Zhang J W 2023 M. S. Thesis (Harbin: Heilongjiang University
[18] Yu W, Qu H, Zhang Y 2023 Sensors 23 7823
Google Scholar
[19] Li Y J, Li Y H, Li F, Zhao B, Li Q Q 2015 Math. Probl. Eng. 2015 854945
Google Scholar
[20] Wei L X, Zhang Y, Ji L I, Ye L, Zhu X C, Fu J 2022 Energies 15 5880
Google Scholar
[21] Zhou Z W, Gong H Y, You J, Liu S B, He J L 2021 Mater. Today Commun. 28 102507
Google Scholar
[22] 周勇 2024 测绘与空间地理信息 47 217
Google Scholar
Zhou Y 2024 Geomatics & Spatial Information Technology 47 217
Google Scholar
[23] Li X, Ke S C, Li Y, Jin W, Fu X H, Fu G W, Bi W H 2024 Opt. Laser Technol. 176 110973
Google Scholar
下载:
计量
- 文章访问数: 398
- PDF下载量: 7
- 被引次数: 0
