-
随着石墨烯等二维材料的发现, 相对论二维Dirac方程越来越受到研究者们的关注, 准确求解电磁场中的Dirac方程是研究和调控Dirac电子量子状态的基础. 通过将分区级数方法应用到Dirac方程中并对该方程在正则区、泰勒区和非正则区进行级数展开, Dirac电子束缚态的普适性判据被推导出来, 束缚态的能级和波函数被计算出来. 用该方法计算有质量Dirac电子在库仑电势下(相对论二维类氢原子)的能级和波函数并与解析解进行比较, 结果表明该方法具有非常高的准确性. 对均匀磁场和线性电势下Dirac电子态的计算结果表明, 该方法对于复杂电磁场中Dirac方程的求解具有普遍的适用性. 用该方法研究了均匀磁场B和线性电势V = Fr下Dirac电子束缚态随着电势强度的变化, 负能态的能级序列变化被观察到, 在临界处F = 0.5B, 正能态的束缚态仍然存在, 而只有能量超过0的少数负能态的束缚态才存在. 该方法提供了求解Dirac方程的有效工具并丰富了人们对相对论量子力学的认识.With the discovery of two-dimensional materials like graphene, the relativistic two-dimensional Dirac equation has received increasing attention from researchers. Accurately solving the Dirac equation in electromagnetic fields is the foundation for studying and manipulating quantum states of Dirac electrons. Sectioned series expansion method is successful and accurate in solving Schrödinger equation under complex electromagnetic fields. Dirac equation is a system of coupled first-order differential equations with undermined eigenvalues, and it is more difficult to solve. By applying the sectioned series expansion principle to Dirac equation and conducting series expansions in regular, Taylor and irregular regions, we obtain an accurate method with wide applicability. With the method, a universal criterion for bound states of Dirac electrons in electromagnetic fields is derived and the energy levels and wave functions of bound states can be accurately calculated. The criterion given in the main text body shows that the magnetic field and mass field help to confine Dirac electrons while the electric field tends to deconfine them due to Klein tunneling. When the highest power of the electric potential is equal to that of the magnetic vector potential or the mass field, confined-deconfiend states depend on the comparison of their coefficients. We apply the method to two cases: one is massive Dirac electron in Coulomb electric potential (relativistic two-dimensional hydrogen-like atom) and the other is Dirac electron in uniform mangetic field (mangetic vector potenial is A = 1/2Br) and linear electric potential V = Fr. The energy levels of the hydrogen-like atom are calculated and compared with analytical solutions, demonstrating the exceptional accuracy of the method. By solving Dirac equation under uniform magnetic field and linear electric potential, the method proves to be broadly applicable to the solutions of Dirac equation under complex electromagnetic fields. Under uniform magnetic field B and V = Fr, as the F increases, level orders of negative energy states change and at the critical point F = 0.5B, the bound states of positive ones still exist while only certain negative ones can exist on condition that their energies exceed zero. The sectioned series expansion method provides an effective computational framework for Dirac equation and it deepens our understanding of relativistic quantum mechanics.
-
Keywords:
- Dirac equation /
- sectioned series expansion method /
- bound states /
- relativistic two-dimensional hydrogen-like atom
[1] Semenoff G W 1984 Phys. Rev. Lett. 53 2449
Google Scholar
[2] Sun S, Zhu J L 2014 Phys. Rev. B 89 155403
Google Scholar
[3] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[4] Feng B, Ding Z, Meng S, Yao Y, He X, Cheng P, Chen L , Wu K 2012 Nano Lett 12 3507
Google Scholar
[5] Gomes K K, Mar W, Ko W, Guinea F, Manoharan H C 2012 Nature 483 306
Google Scholar
[6] Novoselov K S, Geim A K, Morozov S V, Jiang D, Katsnelson M I, Grigorieva I V, Dubonos S V, Firsov A V 2005 Nature 438 197
Google Scholar
[7] Elahi M M, Vakili H, Zeng Y, Dean C R, Ghosh A W 2024 Phys. Rev. Lett. 132 146302
Google Scholar
[8] 陈晓娟, 徐康, 张秀, 刘海云, 熊启华 2023 72 237201
Google Scholar
Chen X J, Xu K, Zhang X, Liu H Y, Xiong Q H 2023 Acta Phys. Sin. 72 237201
Google Scholar
[9] 冉扬强, 薛立徽, 胡嗣柱 2002 51 2435
Google Scholar
RanY Q, Xue L H, Hu S Z 2002 Acta Phys. Sin. 51 2435
Google Scholar
[10] Silbar R R, Goldman T 2010 Eur. J. Phys. 32 217
[11] Kandemir B S, Mogulkoc A 2010 Eur. Phys. J. B 74 535
Google Scholar
[12] Lee C M , Lee R C H, Ruan W Y, Chou M Y 2010 Appl. Phys. Lett. 96 212101
Google Scholar
[13] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y, Mitroy J 2012 Chin. Phys. Lett. 29 063101
Google Scholar
[14] Giavaras G, Maksym P A, Roy M 2009 J. Phys. : Condens. Matter 21 102201
Google Scholar
[15] Zhu J L, Xiong J J, Gu B L 1990 Phys. Rev. B 41 6001
Google Scholar
[16] Ezawa M 2012 New J. Phys. 14 33003
Google Scholar
[17] Fishbane P M, Gasiorowicz S G, Johannsen D C, Kaus K 1983 Phys. Rev. D 27 2433
Google Scholar
[18] Batchelor M T, Henry R A, Lu X 2023 AAPPS Bulletin 33 29
Google Scholar
[19] Zhu J L, Sun S 2012 Phys. Rev. B 85 035429
Google Scholar
[20] 王竹溪, 郭敦仁 2012 特殊函数概论(北京: 北京大学出版社) 第39—58页
Wang Z X, Guo D R 2012 Special Functions (Beijing: Peking University Press) pp39–58
[21] Giavaras G , Nori F 2010 Appl. Phys. Lett. 97 243106
[22] Pereira V M, Nilsson J, Neto A H C 2007 Phys. Rev. Lett. 99 166802
Google Scholar
[23] Novikov D S 2007 Phys. Rev. B 76 245435
Google Scholar
[24] Lukose V, Shankar R, Baskaran G 2007 Phys. Rev. Lett 98 116802
Google Scholar
-
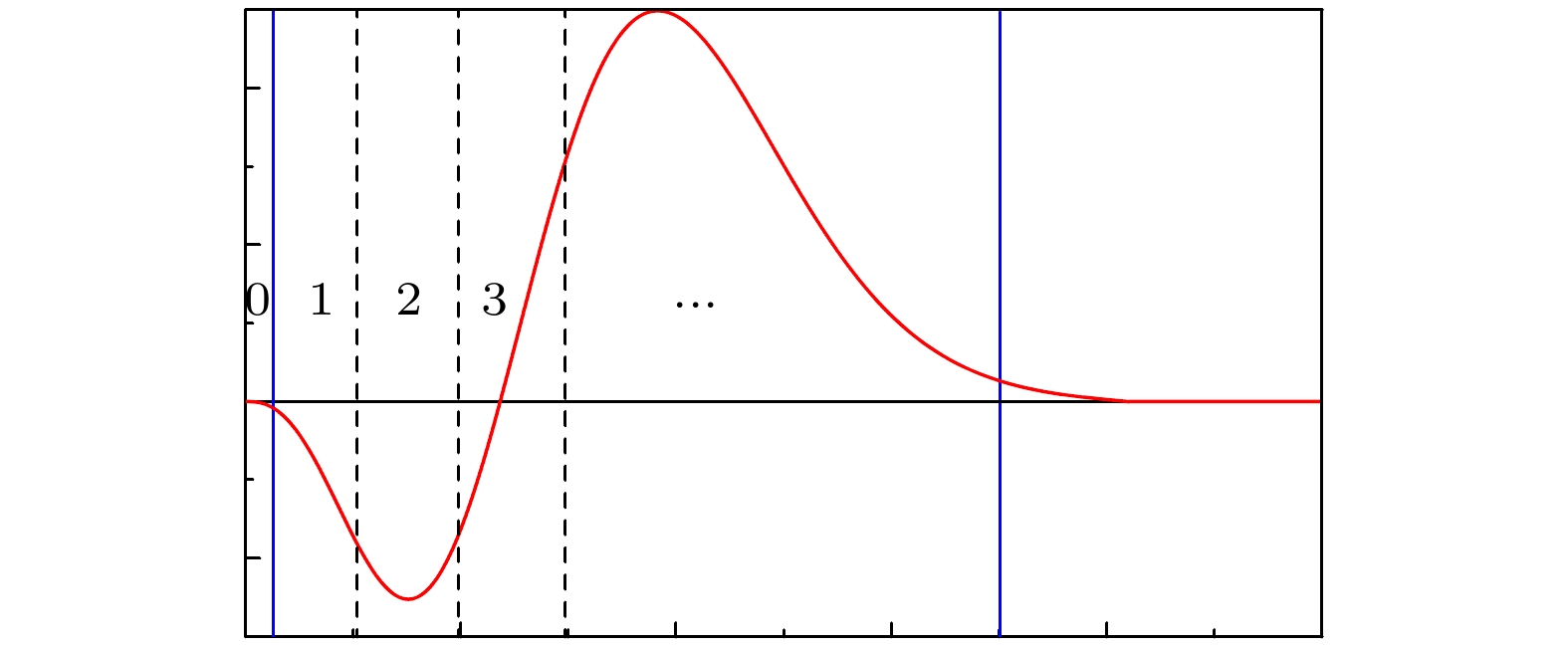
图 1 分区级数解法示意图, 径向波函数在不同区间分别用级数精确表示出来, 第0个区间是正则区(regular region), 最后是非正则区(irregular region), 中间都是泰勒区(Taylor region)
Fig. 1. The sketch of the sectioned series expansion method, the radial wavefunction is exactly expressed by different series expansions in separate regions: The zeroth region is regular one, the last is irregular one and others between them are Taylor ones.
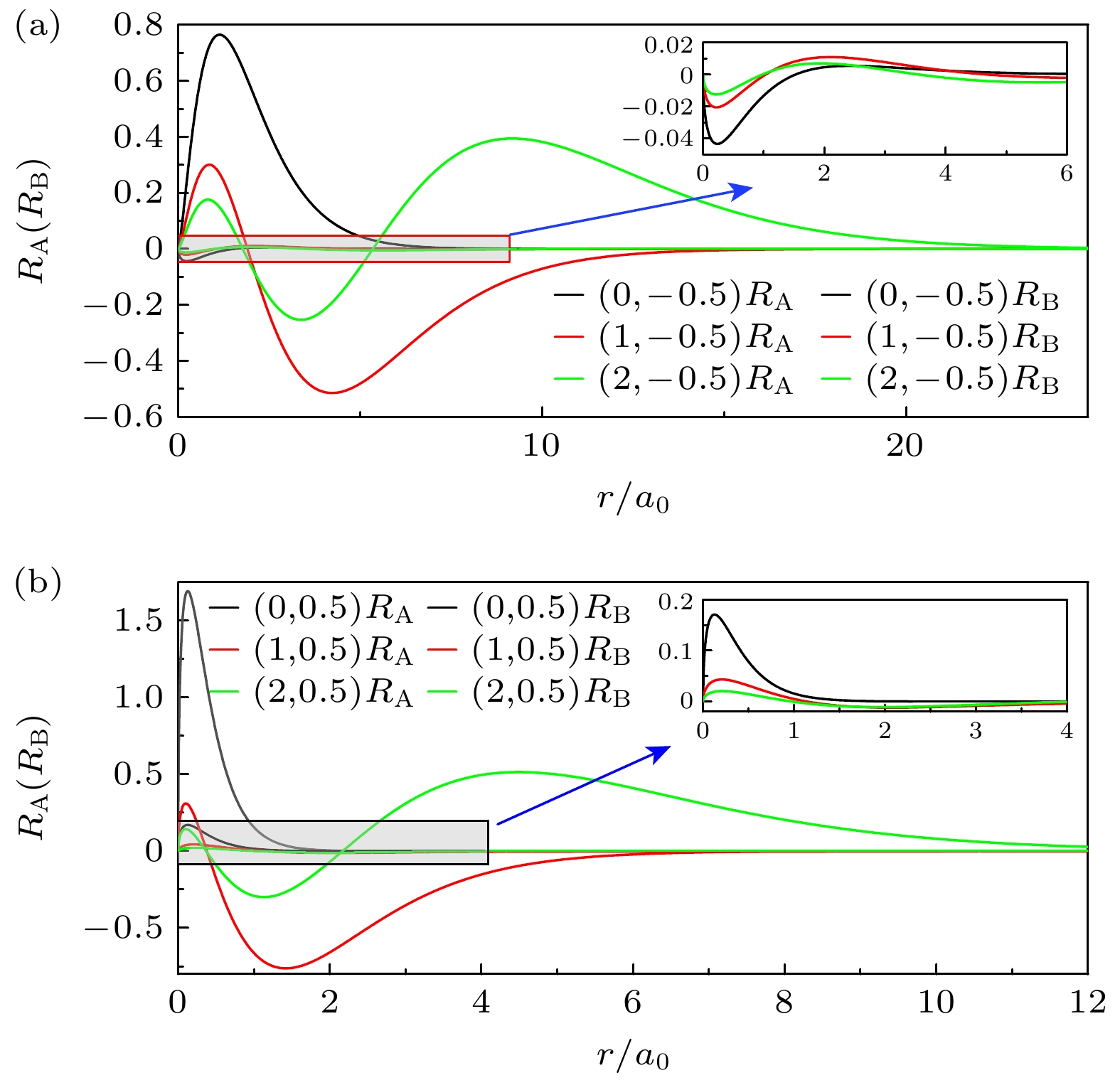
图 2 在库仑电势中的α = –0.1时用分区级数解法计算相对论氢原子能级的径向波函数上下分量(RA和RB), 在计算时取M = 500 meV, 粗线(细线)分别代表上下分量, 右上方的图是对局部波函数的放大, (a), (b)分别是j = –0.5和j = 0.5时最低的3个能级的波函数
Fig. 2. The upper and lower components (RA和RB) of the radial wave function of the relativistic hydrogen atom calculated by sectioned series expansion method when α = –0.1 in the Coulomb electric potential and M = 500 meV, bold (thin) lines represent the upper (lower) components and the insets in the top right are the zooms of parts of the functions: (a), (b) The three lowest energy levels of j = –0.5 and j = 0.5, respectively.
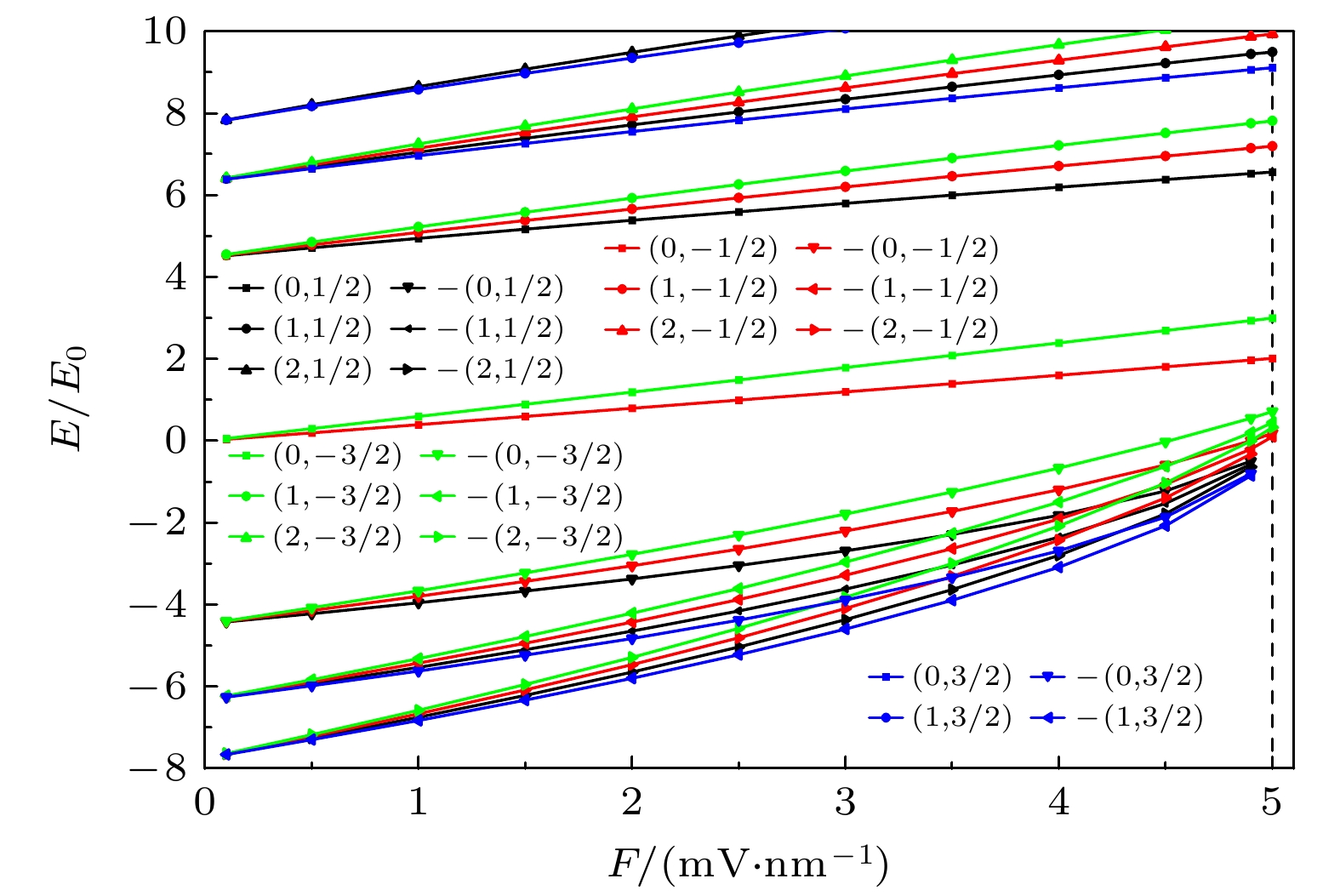
图 3 在均匀磁场B = 10 T时, 总角动量量子数j = –1/2, –3/2, 1/2, 3/2的能级随着线性电势V = Fr的变化, 其中(n, j)前面的负号表示负能态, F = 5时的垂直虚线是为了观察每个能级是否存在束缚态能级
Fig. 3. The energy levels of the total angular momentum quantum number j = –1/2, –3/2, 1/2, 3/2 as a function of the linear electric potential, the minus signs in front of (n, j) indicates the negative energy states, and the vertical dashed line at F = 5 is to observe whether there is a bound state for every energy level.
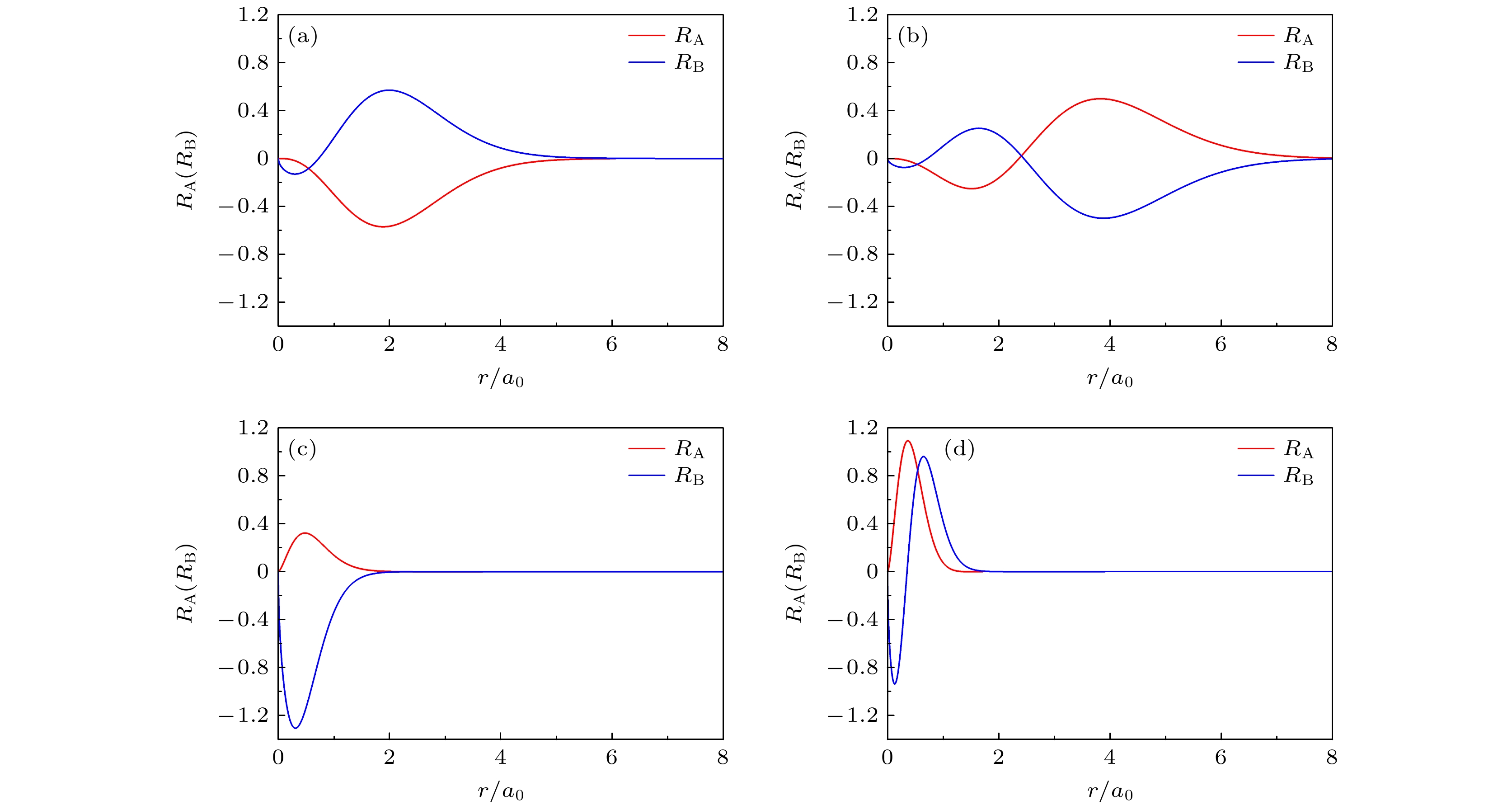
图 4 Dirac电子在F = 0.5B时均匀磁场和线性电势下j = –1/2的径向波函数的上下分量(RA和RB) (a), (b)分别是原来负能态(0, –1/2)和(1, –1/2)在F = 0.5B时转变为正能态的波函数; (c), (d) 分别是原来正能态(0, –1/2)和(1, –1/2)在F = 0.5B时的波函数
Fig. 4. The upper and lower components (RA和RB) of the radial wave function of Dirac electron at F = 0.5B in homogenous magnetic field and linear electric potential when j = –1/2: (a), (b) The original negative energy levels (0, –1/2) and (1, –1/2); (c), (d) the original positive energy levels (0, –1/2) and (1, –1/2).
表 1 在库仑电势中的α = –0.1时用分区级数解法计算相对论氢原子能级的数值解与(53)式的解析解比较, 计算时取M = 500 meV, 能级均除以M
Table 1. Comparison between numerical energy levels by sectioned series expansion method and analytical energy levels by Eq. (53) when α = –0.1 in the Coulomb electric potential and M = 500 meV, with all energy levels divided by M.
(n, j) En, j 数值解 En, j 解析解 相对误差 (n, j) En, j 数值解 En, j 解析解 相对误差 0, –1.5 0.9991988238614 0.99919882386158 1.8×10–13 0, 0.5 0.9797958971133 0.97979589711327 2.9×10–14 1, –1.5 0.9995913079808 0.99959130798090 9.9×10–14 1, 0.5 0.9977551312156 0.99775512256234 8.7×10–9 2, –1.5 0.9997528114902 0.99975281149021 1.4×10–14 2, 0.5 0.9991944716637 0.99919446965227 2.0×10–9 3, –1.5 0.9998345510564 0.99983455105648 7.9×10–14 3, 0.5 0.9995897240939 0.99958972295987 1.1×10–9 0, –0.5 0.9977551536827 0.99775512256234 3.1×10–8 0, 1.5 0.99777530313970 0.99777530313972 1.8×10–14 1, –0.5 0.9991944768698 0.99919446965227 7.2×10–9 1, 1.5 0.99919882386160 0.99919882386158 2.2×10–14 2, –0.5 0.9995897256360 0.99958972295987 2.7×10–9 2, 1.5 0.99959130798070 0.99959130798090 2.0×10–13 3, –0.5 0.9997520675873 0.99975206631993 1.3×10–9 3, 1.5 0.99975281149010 0.99975281149021 1.1×10–13 0, 2.5 0.9991996881893 0.99919967974374 8.5×10–9 2, 2.5 0.99975295828120 0.99975295828121 9.3×10–15 1, 2.5 0.9995916199728 0.99959161997285 4.7×10–14 3, 2.5 0.99983463144880 0.99983463144884 4.0×10–14 
下载: 导出CSV
-
[1] Semenoff G W 1984 Phys. Rev. Lett. 53 2449
Google Scholar
[2] Sun S, Zhu J L 2014 Phys. Rev. B 89 155403
Google Scholar
[3] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666
Google Scholar
[4] Feng B, Ding Z, Meng S, Yao Y, He X, Cheng P, Chen L , Wu K 2012 Nano Lett 12 3507
Google Scholar
[5] Gomes K K, Mar W, Ko W, Guinea F, Manoharan H C 2012 Nature 483 306
Google Scholar
[6] Novoselov K S, Geim A K, Morozov S V, Jiang D, Katsnelson M I, Grigorieva I V, Dubonos S V, Firsov A V 2005 Nature 438 197
Google Scholar
[7] Elahi M M, Vakili H, Zeng Y, Dean C R, Ghosh A W 2024 Phys. Rev. Lett. 132 146302
Google Scholar
[8] 陈晓娟, 徐康, 张秀, 刘海云, 熊启华 2023 72 237201
Google Scholar
Chen X J, Xu K, Zhang X, Liu H Y, Xiong Q H 2023 Acta Phys. Sin. 72 237201
Google Scholar
[9] 冉扬强, 薛立徽, 胡嗣柱 2002 51 2435
Google Scholar
RanY Q, Xue L H, Hu S Z 2002 Acta Phys. Sin. 51 2435
Google Scholar
[10] Silbar R R, Goldman T 2010 Eur. J. Phys. 32 217
[11] Kandemir B S, Mogulkoc A 2010 Eur. Phys. J. B 74 535
Google Scholar
[12] Lee C M , Lee R C H, Ruan W Y, Chou M Y 2010 Appl. Phys. Lett. 96 212101
Google Scholar
[13] Zhang Y H, Tang L Y, Zhang X Z, Shi T Y, Mitroy J 2012 Chin. Phys. Lett. 29 063101
Google Scholar
[14] Giavaras G, Maksym P A, Roy M 2009 J. Phys. : Condens. Matter 21 102201
Google Scholar
[15] Zhu J L, Xiong J J, Gu B L 1990 Phys. Rev. B 41 6001
Google Scholar
[16] Ezawa M 2012 New J. Phys. 14 33003
Google Scholar
[17] Fishbane P M, Gasiorowicz S G, Johannsen D C, Kaus K 1983 Phys. Rev. D 27 2433
Google Scholar
[18] Batchelor M T, Henry R A, Lu X 2023 AAPPS Bulletin 33 29
Google Scholar
[19] Zhu J L, Sun S 2012 Phys. Rev. B 85 035429
Google Scholar
[20] 王竹溪, 郭敦仁 2012 特殊函数概论(北京: 北京大学出版社) 第39—58页
Wang Z X, Guo D R 2012 Special Functions (Beijing: Peking University Press) pp39–58
[21] Giavaras G , Nori F 2010 Appl. Phys. Lett. 97 243106
[22] Pereira V M, Nilsson J, Neto A H C 2007 Phys. Rev. Lett. 99 166802
Google Scholar
[23] Novikov D S 2007 Phys. Rev. B 76 245435
Google Scholar
[24] Lukose V, Shankar R, Baskaran G 2007 Phys. Rev. Lett 98 116802
Google Scholar
下载:
计量
- 文章访问数: 326
- PDF下载量: 10
- 被引次数: 0
